“拓”材有形 “展”智無(wú)痕

劉翠玲

2022版新課程標(biāo)準(zhǔn)提出：數(shù)學(xué)課程要培養(yǎng)學(xué)生“會(huì)用數(shù)學(xué)的眼光觀察現(xiàn)實(shí)世界、用數(shù)學(xué)的思維思考現(xiàn)實(shí)世界、用數(shù)學(xué)的語(yǔ)言表達(dá)現(xiàn)實(shí)世界”，使學(xué)生了解數(shù)學(xué)的價(jià)值，欣賞數(shù)學(xué)美，提高學(xué)習(xí)數(shù)學(xué)的興趣，建立學(xué)好數(shù)學(xué)的信心，形成質(zhì)疑問(wèn)難、勇于探索的科學(xué)精神。隨著新課標(biāo)的落地，我們?cè)絹?lái)越深刻地認(rèn)識(shí)到教學(xué)應(yīng)該從“知識(shí)本位”轉(zhuǎn)變?yōu)椤八仞B(yǎng)本位”。“生本課堂”理念下教師要積極探索發(fā)展學(xué)生核心素養(yǎng)的路徑，不應(yīng)局限于“教教材”，而是要根據(jù)學(xué)生實(shí)際需要靈活地處理教材，對(duì)知識(shí)內(nèi)容、技能、方法進(jìn)行結(jié)構(gòu)化整合與拓展，通過(guò)增加學(xué)習(xí)內(nèi)容的文化性、趣味性、挑戰(zhàn)性，滿足學(xué)生的求知欲，使學(xué)生面對(duì)實(shí)際問(wèn)題時(shí)，能主動(dòng)嘗試著從數(shù)學(xué)的角度運(yùn)用所學(xué)知識(shí)和方法尋求解決問(wèn)題的策略。

下面，以筆者自主開發(fā)設(shè)計(jì)的一節(jié)拓展課《畫圖策略》為例，談?wù)勑抡n標(biāo)理念下小學(xué)數(shù)學(xué)拓展課教學(xué)的思考：

解決問(wèn)題的方法和策略有很多，畫圖策略是其中之一，它是學(xué)生根據(jù)所揭示的數(shù)學(xué)問(wèn)題內(nèi)涵，采用畫圖的方法，把抽象問(wèn)題詳盡化、直觀化，從而達(dá)到解決問(wèn)題之目標(biāo)。畫圖策略是“數(shù)形結(jié)合”思想的詳盡體現(xiàn)，也是最貼合小學(xué)生形象思維特點(diǎn)的有效策略。人教版和蘇教版等教材將解決問(wèn)題的策略作為一個(gè)專項(xiàng)學(xué)習(xí)的內(nèi)容設(shè)置于教材之中，而北師版教材則把畫圖策略滲透到各個(gè)知識(shí)點(diǎn)的教學(xué)過(guò)程中，從一年級(jí)開始，就不斷滲透數(shù)形結(jié)合的思想幫助學(xué)生理解并內(nèi)化知識(shí)。在具體教學(xué)過(guò)程中，發(fā)現(xiàn)畫圖作為數(shù)學(xué)學(xué)習(xí)的重要“腳手架”，但學(xué)生主動(dòng)運(yùn)用的意識(shí)卻極為薄弱，很多學(xué)生借助畫圖解決問(wèn)題的習(xí)慣僅僅是因?yàn)椤袄蠋熞耶嫸嫛保鞘恰拔乙嫛钡闹鲃?dòng)意識(shí)。為了化被動(dòng)為主動(dòng)，讓學(xué)生對(duì)畫圖的價(jià)值有更深刻、直接的體驗(yàn)，現(xiàn)以畫圖策略為主題進(jìn)行拓展課的開發(fā)和設(shè)計(jì)，并在北師版的課堂中進(jìn)行拓展教學(xué)，帶領(lǐng)學(xué)生通過(guò)畫圖的價(jià)值體驗(yàn)、策略形成、內(nèi)化運(yùn)用等三方面，探尋畫圖策略在日常數(shù)學(xué)學(xué)習(xí)過(guò)程中的應(yīng)用，激發(fā)學(xué)生自主作圖的意識(shí)，提高學(xué)生的解題能力。

一、策略形成前——“意會(huì)”與“言傳”觸發(fā)

“深有體會(huì)”與“深度認(rèn)同”是策略接收和內(nèi)化的源動(dòng)力。因此，激發(fā)主動(dòng)性和內(nèi)驅(qū)力成了策略意識(shí)培養(yǎng)的首要之舉。拓展課的內(nèi)容作為數(shù)學(xué)基礎(chǔ)內(nèi)容的有益補(bǔ)充，其內(nèi)容取向基于教材而高于教材，基于學(xué)生而發(fā)展學(xué)生。因此在內(nèi)容的選擇上，應(yīng)該結(jié)合學(xué)生實(shí)際去尋找數(shù)學(xué)核心素養(yǎng)的原始生長(zhǎng)點(diǎn)，基于學(xué)情實(shí)際還原學(xué)生的學(xué)習(xí)常態(tài)，并且通過(guò)生生互動(dòng)而自發(fā)引起生生觸動(dòng)。

示例1：實(shí)驗(yàn)小學(xué)種植園有一塊長(zhǎng)方形菜地，長(zhǎng)10米。在整修重建時(shí)，菜地長(zhǎng)增加3米，這樣菜地的面積就增加了18平方米。原來(lái)菜地的面積是多少平方米？

1. 互動(dòng)中感知——化“繁雜”為“簡(jiǎn)潔”

以純文字表述的形式出示的例題是我們常見(jiàn)的習(xí)題呈現(xiàn)方式。在學(xué)生自主嘗試解答過(guò)程中，發(fā)現(xiàn)學(xué)情不同解題方式也不同，大致有如下兩種：一種是根據(jù)題意直接列式解答；另一種是根據(jù)題意畫出示意圖再解答。先讓畫圖的學(xué)生說(shuō)明意圖：題中的條件比較多，對(duì)文字的閱讀理解比較困難，對(duì)題中數(shù)量關(guān)系的理解有些模糊，從而產(chǎn)生用更簡(jiǎn)潔快速的方法表達(dá)題意的需求。畫圖的策略不在于教師提出的要求，而是學(xué)生基于實(shí)際需求而自主萌生的。其余學(xué)生在對(duì)比辨析中體會(huì)畫圖的必要性、簡(jiǎn)潔性和直觀性，領(lǐng)略畫圖策略對(duì)于整理信息所起到的化繁為簡(jiǎn)的作用。以學(xué)生帶動(dòng)學(xué)生，以互動(dòng)引發(fā)觸動(dòng)，學(xué)生在畫圖解題的過(guò)程中，逐步把抽象的文字轉(zhuǎn)化為形象的圖形，把形式化的數(shù)據(jù)變成具象化的圖像，從而更好地理解已知條件和所求問(wèn)題之間的聯(lián)系，圖形之妙不言而喻。

2. 解析中感悟——化“抽象”為“形象”

在解題過(guò)程中，學(xué)生自主結(jié)合圖形講解思考過(guò)程，充分利用圖形直觀地分析數(shù)量之間的關(guān)系，題中“增加部分的長(zhǎng)就是原來(lái)長(zhǎng)方形的寬”這一關(guān)鍵信息在圖形解析下一目了然，通過(guò)把列式計(jì)算轉(zhuǎn)化為圖形分析，形成解決問(wèn)題的思路，有效實(shí)現(xiàn)數(shù)形結(jié)合，發(fā)揮了形象思維和抽象思維的協(xié)同作用。在變“抽象”為“形象”之間，“意會(huì)”與“言傳”之中體會(huì)畫圖策略之巧妙。

二、策略形成時(shí)——“體驗(yàn)”與“感悟”并舉

“數(shù)學(xué)中的畫圖和推理，歸根結(jié)底都是計(jì)算。”“推理是抽象的計(jì)算，計(jì)算是具體的推理，圖形是推理和計(jì)算的直觀模型。”在學(xué)生解決問(wèn)題的過(guò)程中，畫圖不是最終目的，畫圖只是一種中介，畫圖是為了更好地輔助思維。充分利用“圖形”這種形象直觀的表達(dá)方式，讓其成為學(xué)生學(xué)習(xí)路上的“腳手架”則意義非凡。

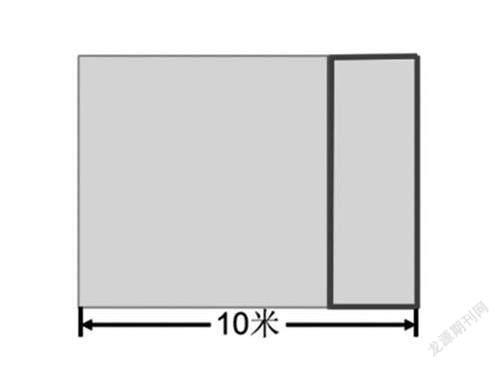
示例2：學(xué)校種植園菜地長(zhǎng)10米，劃分出一個(gè)最大的正方形種白蘿卜，剩下的部分要用籬笆圍起來(lái)，求籬笆的長(zhǎng)度是多少米？

1. 實(shí)踐中萌發(fā)——有感而“畫”

圖形與幾何領(lǐng)域的知識(shí)相對(duì)較為抽象，畫圖策略的作用尤其凸顯。例2是長(zhǎng)方形周長(zhǎng)知識(shí)的靈活應(yīng)用，這個(gè)問(wèn)題不同于一般的簡(jiǎn)單實(shí)際問(wèn)題，雖然題干簡(jiǎn)潔卻很抽象，學(xué)生自主解題的過(guò)程中經(jīng)過(guò)例1的啟發(fā)而自覺(jué)使用畫圖策略的同學(xué)已達(dá)90%左右，學(xué)生自覺(jué)借助畫圖幫助理解題意，由此可見(jiàn)自主意識(shí)已被喚醒。

2. 轉(zhuǎn)化中明理——化難為易

僅僅會(huì)借助圖形整理信息還無(wú)法體現(xiàn)畫圖的價(jià)值，圖形除了能夠幫助整理題中信息理解題意以外，更重要的是幫助解題。這道題要求學(xué)生摒棄固化思維——依賴長(zhǎng)方形的周長(zhǎng)計(jì)算公式解決問(wèn)題，要運(yùn)用轉(zhuǎn)化的思想——“一長(zhǎng)一寬的和=原長(zhǎng)方形的長(zhǎng)”來(lái)解決問(wèn)題。

為了更好地凸顯“生本課堂”，建立基于學(xué)生立場(chǎng)的“簡(jiǎn)教深學(xué)”的課堂新樣態(tài)。在課堂中教師留足時(shí)間和空間先讓學(xué)生自主探究，再借力小組合作探究，嘗試解決問(wèn)題。交流過(guò)程中發(fā)現(xiàn)不同思維水平的學(xué)生呈現(xiàn)了三種不同的生成：

生1：無(wú)法解答——這道題信息不完整，沒(méi)有告訴我們寬是多少，所以沒(méi)法解答；

生2：假設(shè)法——假設(shè)劃分的正方形邊長(zhǎng)是9米，因此剩余的長(zhǎng)方形的寬是1米，（9+1）×2=20（米）；

生3：轉(zhuǎn)化法——不論原來(lái)長(zhǎng)方形的寬是多少，剩余的長(zhǎng)方形一長(zhǎng)一寬的和=原來(lái)長(zhǎng)方形的長(zhǎng)=10米，因此籬笆的長(zhǎng)是10×2=20（米）；

可見(jiàn)會(huì)畫圖的同學(xué)占大部分，會(huì)讀圖且用圖的卻不多，大部分學(xué)生不懂利用圖形挖掘文字層面看不到的隱藏的信息。在集體交流時(shí)，第2位學(xué)生的假設(shè)法受到部分同學(xué)的反駁和質(zhì)疑——如果正方形的邊長(zhǎng)是9.9呢？由此可見(jiàn)這樣的方法只是特例，不夠有說(shuō)服力。而第3位同學(xué)結(jié)合正方形四條邊都相等的特點(diǎn)，帶領(lǐng)同學(xué)借助圖形觀察、分析、轉(zhuǎn)化、推理，最終發(fā)現(xiàn)：“不管原來(lái)長(zhǎng)方形的寬是多少，剩下圖形的一長(zhǎng)一寬的和始終都是10米。”依圖形助力，在觀察中轉(zhuǎn)化，轉(zhuǎn)化中推理，推理中解題，學(xué)生豁然開朗，圖形的價(jià)值不言自明。

教學(xué)過(guò)程中， 從“會(huì)畫圖”到“會(huì)用圖”，生生互動(dòng)中“寓理于形”，學(xué)生感悟到畫圖策略能把原本隱藏的關(guān)系更加形象明了地顯示出來(lái)，畫圖不僅化繁為簡(jiǎn)，還能化難為易。充分凸顯學(xué)科實(shí)踐的意義，學(xué)生在“深有體驗(yàn)”與“深刻感悟”之中感受到策略價(jià)值，策略意識(shí)的根植水到渠成。

三、策略形成后——“思考”與“內(nèi)化”并進(jìn)

學(xué)習(xí)不是一蹴而就的，學(xué)生學(xué)習(xí)“解決問(wèn)題的策略”也不是“一步到位”，而是在步步思索、層層體驗(yàn)中理解和掌握的。因此，教師突破思維固守的“畫圖”僅適用于“圖形與幾何”領(lǐng)域的錯(cuò)誤認(rèn)知，不斷開拓策略運(yùn)用的時(shí)空領(lǐng)域，通過(guò)回顧與分析、變式與對(duì)比、感悟與體驗(yàn)等渠道，拓寬知識(shí)面，讓學(xué)生在不同領(lǐng)域中感受策略價(jià)值，在不斷豐富認(rèn)知的過(guò)程中內(nèi)化和提升，使學(xué)生對(duì)“畫圖”策略達(dá)到深刻理解、深度掌握和自發(fā)運(yùn)用的水平。

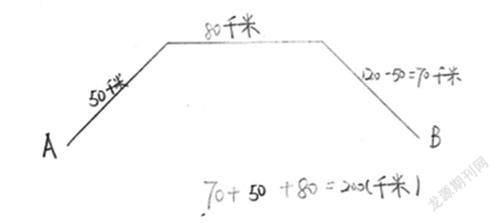
示例3：從A鎮(zhèn)到B鎮(zhèn)，其中上坡路有50千米，平路80千米，其余的是下坡路，一輛車從A鎮(zhèn)到B鎮(zhèn)，往返走一趟，共走了120千米上坡路，從A鎮(zhèn)到B鎮(zhèn)相距多少千米？

1. 領(lǐng)域拓展——“圖”盡其用

將畫圖的策略由圖形領(lǐng)域延伸到生活中的其它領(lǐng)域，打破思維局限，引發(fā)學(xué)生的認(rèn)知沖突——并不是只有解決圖形問(wèn)題才需要畫圖，在其它領(lǐng)域中圖形的作用一樣凸顯，幫助學(xué)生實(shí)現(xiàn)不同領(lǐng)域的跨越，實(shí)現(xiàn)知識(shí)點(diǎn)的溝通與聯(lián)系，讓學(xué)生充分體驗(yàn)畫圖策略的廣泛運(yùn)用的價(jià)值所在。解題過(guò)程中，學(xué)生借助圖形分析，發(fā)現(xiàn)去時(shí)的下坡路在返回時(shí)則成了上坡路，因此，“上坡路共120千米”這內(nèi)隱的條件便直觀地外顯出來(lái)，用圖說(shuō)話，以圖解意。

2. 內(nèi)化策略——“圖”說(shuō)精彩

以圖助力，難點(diǎn)破解，整道題迎刃而解：根據(jù)“120米上坡路”而推理得出返回時(shí)的上坡路為120-50=70千米，故而兩地的三段距離都清清楚楚；還有些思維水平較高的同學(xué)根據(jù)圖意直接用“120+80=200千米”解決問(wèn)題，原本抽象的題，變得簡(jiǎn)單明了。以圖為具，“圖”若畫開，策略自來(lái)。

課時(shí)有限，內(nèi)容有限，但帶給學(xué)生的體驗(yàn)和感悟卻是無(wú)限的。隨著學(xué)習(xí)的深入，雖然學(xué)生所遇到問(wèn)題的類型在不斷變換，而解決這些不同類型問(wèn)題的策略卻始終如一，學(xué)生對(duì)畫圖策略的感悟和運(yùn)用越來(lái)越嫻熟，對(duì)策略的理解也越來(lái)越深刻，從而“數(shù)形結(jié)合”“變與不變”“化歸”等重要的數(shù)學(xué)思想便在無(wú)形中滲透進(jìn)而內(nèi)化為學(xué)生的素養(yǎng)。解決問(wèn)題教學(xué)并不是單純地在“解決問(wèn)題”，而是解決學(xué)生思維方面的“問(wèn)題”：讓學(xué)生學(xué)會(huì)在錯(cuò)綜復(fù)雜的事物中把握本質(zhì)，進(jìn)而提升抽象能力；會(huì)在雜亂無(wú)章的事物中理清頭緒，進(jìn)而培養(yǎng)推理能力；會(huì)在千頭萬(wàn)緒的事物中發(fā)現(xiàn)規(guī)律，進(jìn)而增強(qiáng)建模能力。這樣的課，才是靈動(dòng)的、生長(zhǎng)的，才是根本的、智慧的，才是我們的課堂追求。

新課標(biāo)理念下，我們要基于單元整體視角建構(gòu)知識(shí)體系，對(duì)新授課的課時(shí)進(jìn)行必要的整合和提升，并在必要的教學(xué)中引入一些拓展性內(nèi)容，如以核心知識(shí)點(diǎn)為主題的拓展、以開放的習(xí)題為主題的拓展、以數(shù)學(xué)閱讀內(nèi)容為主題的拓展、以數(shù)學(xué)益智游戲、數(shù)學(xué)趣題名題難題的拓展等等，讓豐富性、多樣性、探究性的學(xué)習(xí)內(nèi)容為學(xué)生的數(shù)學(xué)學(xué)習(xí)注入新的活力，注重引導(dǎo)學(xué)生在動(dòng)手操作、實(shí)踐探索等活動(dòng)中發(fā)現(xiàn)知識(shí)，感受數(shù)學(xué)學(xué)習(xí)的趣味性，享受探究的樂(lè)趣，領(lǐng)略數(shù)學(xué)的魅力所在，全面提升他們的觀察、分析、判斷、想象、創(chuàng)造等各方面的能力，從而提升學(xué)生的數(shù)學(xué)素養(yǎng)。

“拓”教有形，“展”智無(wú)痕。數(shù)學(xué)教學(xué)并不僅僅是知識(shí)的教學(xué)，更是智慧教學(xué)，學(xué)生的學(xué)習(xí)不是簡(jiǎn)單的獲取知識(shí)，而是在獲取知識(shí)的過(guò)程中發(fā)展思維能力，提高解決問(wèn)題的能力。讓我們帶著學(xué)生在有限的時(shí)間里暢游魅力無(wú)限的數(shù)學(xué)海洋，從“有知識(shí)的人”走向“有智慧的人”。

*本文系泉州市教育科學(xué)“十四五”規(guī)劃（第一批）課題《小學(xué)中年級(jí)數(shù)學(xué)拓展課的開發(fā)與設(shè)計(jì)》（編號(hào)：QG1451-055）的研究成果。