打磨細節，盤活知識，成就精彩數學課堂

［摘? 要］ 教師只有預設和打磨好每一個教學細節，才能盤活每一個知識點，將新的教學理念落到實處，讓課堂教學更加有效，成就精彩數學課堂。教師打磨細節的策略主要有：趣味預設細微處，確保流暢；準確打磨關鍵點，減少出錯；機智解決模糊層，切身體驗；拓展思維空間時，彰顯個性。

［關鍵詞］ 細節；數學知識；精彩課堂

課堂教學由多個教學環節構成，而每個教學環節又包含了一些教學細節。高爾基說，細節是隱藏在文字間的魔術。對于數學課堂而言，最能體現課堂精彩的莫過于散落在教學環節中的那些閃光的細節。教學“細節”雖然意指“細小的枝節”，但體現了教師的教學理念、教學經驗和教學機智。因此，教師只有預設和打磨好每一個教學細節，才能盤活每一個知識點，將新的教學理念落到實處，讓課堂教學更加有效，成就精彩數學課堂。

一、趣味預設細微處，確保流暢

預設就是根據數學教學的內容、數學教學的目標和學生已有的認知水平，優選教學手段、教學技巧和教學方法，系統地規劃數學教學的過程，使數學教學活動能按一定的程序正常開展。預設針對生成而言，兩者既相互依存又相對獨立。雖然生成并不會受到預設的制約，但是成功、有效、精準的預設能夠讓生成更加精彩。因此，對于數學課堂教學，教師應該認真細致地進行預設，預設得越成功、越有效、越精準，生成就會越精彩，數學的教學就會越流暢。

課前準備是否充分，很大程度上決定了一節課的成敗。課前準備充分，則有了精心的預設，課也就會上得得心應手；課前準備倉促，則失去了有效的預設，課常常會上得雜亂無章。可見，充分而合理的預設對課堂教學十分重要，直接關系到教學的效率和教學的質量。那么，課前教師需要有策略地預設。小學生都是活潑的生命個體，有趣的事物往往更能吸引他們的注意力。教師可以預設趣味性的細節，讓學生興趣盎然地進行思考、探究和學習，讓小細節發揮大效果，確保課堂教學的流暢。

案例1? 四則混合運算

師：四則混合運算已經學完了，下面我們來理一理運算順序，大家有沒有興趣呢？

生（齊）：有！

師：好。現在需要在“括號內、乘除和加減”3個中選一個做“老大”，你們選哪一個？

生（異口同聲）：括號內。

師：誰能說一說選它的理由是什么？

生1：括號內的需要先算，所以它做“老大”沒人有意見，都得為它讓路。（其余學生哄堂大笑）

生2：在計算時，首先考慮括號內的運算，所以它是“老大”。

師：你們的理由非常充分，那“老大”選完了，“老二”是誰呢？

生3：乘除。

師：理由呢？

生3：如果“老大”不在，運算時先算乘除，后算加減，所以乘除自然是“老二”。

師：只剩下“加減”了，那它就是“老三”。今天我們給它們安排了一個“輩分”，你們記住了嗎？運算順序有沒有理清呢？還會出錯嗎？

……

經過這樣一番整理復習，讓運算順序有了各自的“輩分”，使學生獲得了深刻的理解和認識。之后，只要解答四則混合運算，筆者總能聽見學生自言自語：“先看有沒有老大……”顯然，正是由于教師抓住了運算順序的本質，以幽默的語言讓學生在細節處領會了其中的奧秘。這樣的教學不僅有趣，也很流暢，學生自然學得輕松，更重要的是有效提升了自身的計算能力。

二、準確打磨關鍵點，減少出錯

學生做數學題，經常會出錯。尤其是題目數量越多，運算步驟越多，學生出現的錯誤也越多。學生雖然知道計算不能馬虎、不能粗心，但很難實現“零出錯”。大多數學生都意識不到自己出現的錯誤，盡管學生進行了驗算或復查，但就是發現不了自己的錯誤。對此，教師不能單純地運用“判錯→講評→更正”的教學方式，需要在平時的教學中準確打磨關鍵點，引導學生有意識地觀察題目的特征，根據運算過程的規律，利用相應的算理，減少出錯，提高正確率。

小學數學中關于計算的重要性無須多言，計算是數學學習的一項基本技能。可以說，一旦學生計算的準確性提高了，那么他的數學成績也就提高了。無論課程改革如何深入，無論計算器多么先進，教師都需要教會學生基本的口算與筆算，提高學生的計算能力。因此，針對計算教學，教師需認真推敲和周密設計每一個教學細節，尤其要對教學的關鍵內容精心打磨，以減少學生的出錯，為提高他們的計算能力而努力。

案例2? 三位數減兩、三位數（退位）的減法

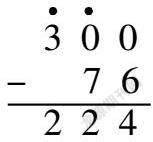
分析：對于300-76的計算，根據筆者多年教學的經驗可以發現不少學生容易計算為300-76=234。針對這一情形，筆者深入思考和設計了以下教學過程：

師：剛才我們重點討論了計算算法，下面讓我們一起來交流豎式計算。

師：我們一起來看這個豎式，老師希望大家將重要部分圈起來，你覺得哪里需要圈？并說一說原因。

生1：我會圈中間0上面的“·”，因為算式中個位上的0減6不夠，需要向十位上借一當十。

生2：我會圈3上面的“·”，因為中間0不夠減7，需要向百位上借一。

師：你們真是有想法的好孩子，回答得特別好！其他同學是不是也認可他們的觀點需要將兩個“·”圈起來？（其余學生點頭表示贊同）

師（拾級而上）：那其他人還有沒有想法呢？

生3：我覺得可以將得數中間的2圈一圈。

師：老師也這樣認為，你能告訴大家為什么嗎？

生3：中間的0被個位“借走一個”，即便它再向百位借一，也是沒有10個十的，而是只有9個十，這里需要注意到“9個十減7個十是2個十”，所以這里的2很關鍵，一定要圈一圈。

……

不可否認，正是因為教師精準切入，引起了學生的辯論、質疑和反思，通過“圈一圈”將每一個關鍵點羅列出來，引起學生足夠的關注和重視，才使得之后的練習和作業都能“引以為戒”，提升計算的正確率。在后續的教學實踐中可以發現，不管是連續進位問題，還是退位加減豎式計算，學生的出錯率大大減少了。顯然，如此精心打磨的課堂給予了學生積極的情感體驗，課堂教學富有成效。

三、機智解決模糊層，切身體驗

課堂教學是通向未知領域的旅行，意味著教學存在隨機性和偶發性。只有在教學過程中彰顯細節處理的價值，才能通過創意、精彩的細節閃現教師的教學智慧。新課程標準強調教學需要通過動手操作讓學生“動”起來，在切身體驗中更好地構建數學知識。這就需要教師設計好有效的操作活動，從知識的模糊層面出發深入挖掘其中蘊含的教學真諦，做好機智的處理，給予學生真實的體驗，讓枯燥的數學教學變得具有生命活力，讓課堂因此而精彩。

案例3? 認識“＞、＜”

分析：一年級的學生對數的認識十分模糊，常常很難將符號與數很好地聯系在一起，容易造成混淆。因此，“認識＞和＜”的教學對于教師來說難度較大。不少教師會選擇編口訣讓學生記憶，但效果很難盡如人意。為了促進學生的理解，筆者在細節處細致打磨，設計了以下教學過程。

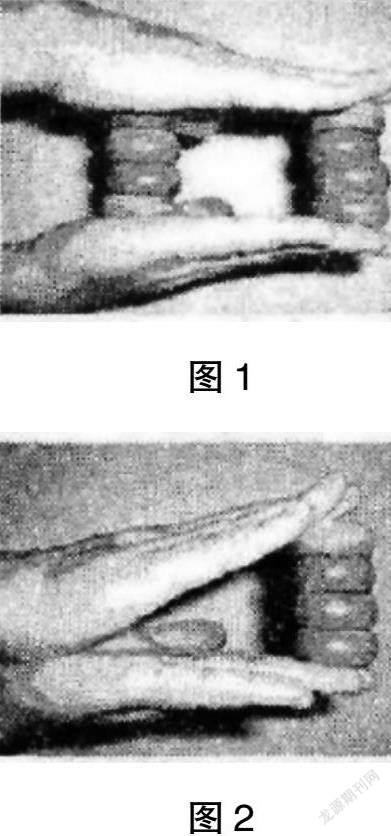
師：大家看，老師手掌前后各有多少顆象棋呢？（教師實物演示，如圖1）

生1：都是4顆，前后數目一樣多。

師：你們聯想一下，像數學中的哪個符號？

生2：像等號。

師：真是觀察仔細、想象豐富的好孩子。

師：那現在呢？老師拿掉了一邊的棋子，現在像數學中的哪個符號？（教師演示圖2）

生3：像大于號。

師：從剛才兩邊一樣多的棋子，到現在一邊沒有一邊有，有的那一邊可以說是比較大……

生4：開口大的一邊有4顆象棋，另一邊沒有。

生5：開口大的一邊象棋數多。

生6：符號開口朝哪邊，哪邊就大。

……

師：你們說得真好，請大家也試一試操作一下，讓你的同桌去猜一猜“＞”還是“＜”，好不好？

……

教師在教學中要認識到學生數學探究的重要性，清楚把握數學知識和學生認知的模糊層面和疑難點，想方設法為教學設計各種方法，才能在具體教學中發揮主導作用，提升活動設計的實效性。以上案例中，教師從自身的教學經驗出發，基于學生認知的模糊層面，捕捉精彩的、具有價值的教學細節豐富教學，引導學生進行觀察、思考、操作、討論和辨析，讓學生獲得對“＞和＜”的深刻理解，從此告別“大小不分”的情形。

四、拓展思維空間時，彰顯個性

思維對小學生而言，一般可分為直觀動作思維、具體形象思維和抽象邏輯思維。在小學數學教學中，教師應想方設法地訓練學生的思維，引導學生通過解決數學問題拓展思維空間，讓學生的各種思維融會貫通，使學生的數學學習過程多姿多彩，使學生的數學課堂“風生水起”，使學生的知識個性化建構“風調雨順”。

案例4? 一個紙巾卷的上、下底面是環形，環形的外圓半徑（R）是4厘米，內圓半徑（r）是2厘米，紙巾的厚度是0.02厘米。如果把這個紙巾卷的紙巾全部打開拉直，全長約是多少？

教師要求學生先分析題意，再獨立思考，最后在各自的學習小組里討論交流。全班展示交流時，出現了三種解法。

解法1：紙巾卷是由一圈又一圈的圓圍起來的，紙巾有厚度，一圈又一圈的圓，周長會依次增加，構成等差數列。運用“等差數列求和的公式”，可以計算出這個紙巾卷中紙巾的全長。環形內圓周長：C=2πr=2×3.14×2=12.56（厘米）。環形外圓周長：C=2πR=2×3.14×4=25.12（厘米）。紙巾卷中紙巾的圈數：（4－2）÷0.02＝100（圈）。因為紙巾的全長是環形中所有圓的周長總和，所以用“等差數列求和的公式”可以求出紙巾卷中紙巾的全長：（12.56＋25.12）×100÷2＝1884（厘米）＝18.84（米）。

解法2：紙巾卷是由一圈又一圈的圓圍起來的，紙巾有厚度，一圈又一圈的圓，周長不相等且一圈比一圈長，圓的周長依次增加構成等差數列。根據“平均數的思想”，可以用平均圓周長乘紙巾的圈數，求出紙巾的全長。環形內圓周長：C=2πr=2×3.14×2=12.56（厘米）。環形外圓周長：C=2πR=2×3.14×4=25.12（厘米）。平均圓周長：（12.56＋25.12）÷2＝18.84（厘米）。紙巾卷中紙巾的圈數：（4－2）÷0.02＝100（圈）。紙巾卷中紙巾的全長：18.84×100＝1884（厘米）＝18.84（米）。

解法3：如果先在紙巾卷一面的環形上涂紅色，再打開一小段拉直，就會發現紙巾卷中紙巾的一側是一條細長的紅線。可想而知，當把紙巾卷上的紙巾全部打開拉直時，紙巾卷紙巾的一側就是一個又細又長的紅色長方形。紅色長方形的長，就是紙巾卷中紙巾的全長；紅色長方形的寬，就是紙巾卷中紙巾的厚度；紅色長方形的面積，就是紙巾卷一面的環形面積。用環形面積（紅色長方形的面積）除以紙巾的厚度（紅色長方形的寬），就可以求到紙巾卷中紙巾的全長。環形面積：S=πR2－πr2=3.14×42－3.14×22=37.68（平方厘米）。紙巾卷紙巾的全長：37.68÷0.02＝1884（厘米）＝18.84（米）。

顯而易見，案例4中求紙巾卷紙巾全長的三種解法，學生交叉運用了直觀動作思維、具體形象思維和抽象邏輯思維。這些思維在特定的情況下，有可能是相對獨立的，也有可能是相互交叉的。學生運用這些思維，能夠揚長避短，相互協調，相互補充，彰顯個性，拓展思維的空間。

總之，關注教學細節，就是關注教師自身的教學行為是否基于新課程的要求塑造的，也就是追求數學教學的智慧化、精確化和合理化的體現。教師精心打磨教學細節，不僅可以盤活數學知識，讓教學過程更具體、更豐富、更充實，而且可以突出教學重點，凸顯教學亮點，讓學生陶醉其中，綻放個性魅力，成就精彩數學課堂。

作者簡介：沈斌興（1974—），專科學歷，中小學一級教師，從事小學數學教學工作。