精講習題注重轉化技巧 提高思維減輕作業負擔





[摘? 要] 文章剖析了小學生解決問題能力薄弱的原因,提出在教學實踐中要關注學生思維角度的轉化,即從情境、條件、句式、數量關系這四個維度進行轉換,加強學生數學解題技巧的訓練,提升學生的解題能力,為學生減負提供現實抓手。
[關鍵詞] 數學解題;轉換;解題能力;減負
解決問題是小學數學教學的重點與難點,但現實中有部分學生在解決綜合性強、思維性強的實際問題時總是“毫無頭緒”和感到苦惱。究竟是什么原因導致了學生思維受阻呢?筆者認為,主要原因是學生思維角度的錯位,沒有領悟這類問題的思維特征與基本思想,探尋不到條件與條件、條件與問題間的聯系,對題目中的關鍵性條件與關系不能準確地轉化。針對上述現象,筆者在教學實踐中著重關注學生思維角度的轉化,加強學生數學解題技巧的訓練,收到了良好的教學效果。
一、分析情境,轉化成熟悉的情境,讓學生在頓悟中解題
在做題時,學生常常覺得每一道題目都很陌生;而在講評時,教師稍做點撥學生就覺得非常熟悉。這是為什么呢?事實上是因為編題者所設計的陌生情境讓學生無法弄清題目的條件。因此,在教學中教師需要引導學生深入分析情境和學會將陌生情境巧妙地轉化為熟悉情境,才能讓學生看清問題的本質,在頓悟中解題和提升解題能力。
例1? 星期五,全校衛生清理日,三年級(3)班開始打掃衛生,學生帶來了抹布擦洗瓷磚(男女生都有)。若男女生都擦洗,每個人要擦洗6塊;若讓所有女生擦洗,每個人要擦洗18塊。若只讓所有男生擦洗,每個男生要完成多少塊?
分析:初看題目,不少學生會認為這是一道整數應用題,認真讀題后卻發現本題條件不清楚,比如總人數不知、瓷磚數量不知、男生人數不知、女生人數也不知,這些“不知”讓學生深感棘手。此時,教師可以點撥學生轉化題目的情境,試著將其轉化為數量關系相同的問題來探尋解決問題的思路。
這里,教師鼓勵學生變陌生為熟悉,將一道陌生情境問題改編成一道典型的工程問題,使得后續的分析和解題變得簡單,在教會學生解題技巧的同時培養了學生“化生為熟”的思維品質。
二、分析條件,轉化成簡單的關系,探尋解題的突破口
解決問題的過程是不斷去變化題目的過程。轉化思想就是轉化觀察的角度、轉化思考的方式、轉化表達的語言、轉化處理的觀點,在朝著利于問題解決的方向不斷轉化的過程中,將條件間的關系轉化得更加簡單,直至探尋到解決問題的突破口。教學中,不少學生常常抱怨分數的實際應用問題條件繁雜,不易解決,在練習中頻頻出錯。尤其是面對條件中“1”分率單位不同時,學生往往會思維卡殼,完全找不到解決問題的入口。
因此在教學中教師應教會學生分析條件,找尋到不變的量來統一條件中的單位“1”,這樣就可以將復雜的條件關系轉化成簡單的關系,以獲得解決問題的思路。
分析:讀題后,發現例2中有兩個條件中包含分率,分別以芳芳和紅紅帶的錢為單位“1”,而當芳芳借了紅紅60元之后,兩個人身上的錢就都有了變化,使得學生的解題難度又增加了。該如何解決呢?顯然,根據上述條件,教師需提醒學生解決本題時要牢牢把握其中不變的量,是什么呢?再次讀題后,學生可以得出一直不變的量是“紅紅與芳芳兩人錢的總數”。探究到此,只需要轉化條件就可以讓問題迎刃而解了。
就這樣,師生通過深入分析條件,把握住條件中不變的量,進一步完成由復雜到簡單的轉化,在不改變題意的情況下讓變化的量轉化為一定的量,讓問題變得簡單易懂,讓解題事半功倍。
三、分析句式,轉化成相同的句式,讓問題本質明朗化
可見,分數實際應用問題數量關系復雜,尤其是當單位“1”各不相同時學生理解起來難度較大。但借助于分析句式,并將其轉化為相同的句式,可以使得問題本質明朗化,讓學生輕松解題。
四、分析數量關系,轉化成直觀的圖形,讓問題輕松獲解
一般來說,若能將一個特定問題轉化為一個圖形,則可以整體把握住解決問題的思路,從而創造性地獲得解決問題的解法,這即為“數形結合”思想。小學生的抽象思維并不發達,在解決問題中,倘若能以形象性的圖形作為引線,則可以讓抽象的問題變得直觀,讓問題輕松獲解。因此,在解題中,教師需指導學生分析數量關系,合理利用數形結合將抽象的數量關系轉化為直觀的圖形,去簡化解題過程,達到良好的解題效果。
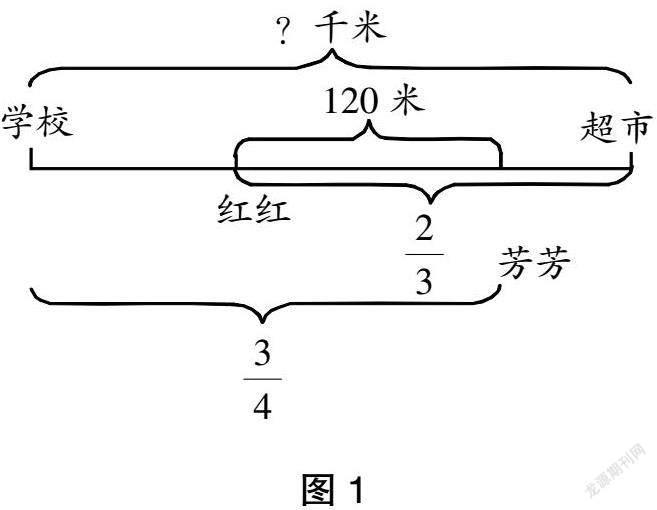
分析:本例是一道典型的行程問題,其中關鍵點有“同時”“兩地”“相向”。深入分析這些關鍵條件,可以得出芳芳和紅紅相遇后繼續向前行駛且都沒有到達目的地。事實上,此類題目學生很少遇到,自然無法理清題目中復雜的數量關系,陷入了解題困境。而此時若能作出線段圖,則可以直觀探尋到120米的對應分率,讓復雜的數量關系變得直觀形象,使問題輕松獲解。
于是,教師點撥學生作出如圖1所示的線段圖,這樣一來,題目中的數量關系變得一目了然,學生可以很快從多個角度入手列出算式,獲得答案“288米”。
“數”抽象概括,“形”形象具體。上例中,教師從小學生的思維特征入手,引導學生巧妙利用數形結合,將抽象的數量關系轉化為直觀的線段圖,充分發揮直觀對抽象的作用,觸及問題的本質,方便問題的分析與解決。
總之,數學解決問題雖然情境復雜、綜合性強,但絕大多數題目有法可依、有路可循。在日常教學中,教師需要一以貫之地培養學生的轉化意識,強調轉化情境、轉化條件、轉化句式、轉化數量關系。這樣可以讓解題“峰回路轉”,能夠訓練和培養學生解決問題的技巧,提升和發展學生的解題能力和思維能力,從而切實減輕學生數學作業負擔。
作者簡介:唐海林(1984—),中小學一級教師,從事小學數學教學工作。

