基于優化SVRM的輸電線路短時期覆冰厚度預測模型研究

湯偉 桑旬 劉家兵 武健

摘?要：針對目前輸電線路覆冰預測誤差大、效率低等問題，提出了一種基于優化SVRM的輸電線路覆冰厚度預測模型.首先運用主成分分析法（PCA）提取出影響線路覆冰的主要特征，其次利用粒子群算法（PSO）對支持向量回歸機（SVRM）中的主要參數進行迭代最優化，同時搭建輸電線路覆冰預測模型.最后結合四川電力勘探設計院某觀冰站自動監測系統采集的現場2 234組覆冰氣象數據集，對所提出的預測模型進行訓練與測試，驗證預測模型的有效性與實用性.與未優化及同類型預測方法相比，其預測平均均方誤差分別減少了約28%、21%、3%，預測準確度有一定的提高.

關鍵詞：輸電線路；自動監測；覆冰預測；主成分分析；支持向量回歸機

中圖分類號：TM733

文獻標志碼： A

文章編號：2096-398X（2023）04-0151-07

Abstract：Aiming at the problems of large error and low efficiency of transmission line icing prediction，a prediction model based on optimized SVRM is proposed .Firstly，principal component analysis （PCA） is used to extract the main features affecting line icing.Secondly，particle swarm optimization （PSO） is used to iteratively optimize the main parameters of support vector regression machine （SVRM），and the icing prediction model is established at the same time.Finally，combined with the 2 234 sets of field icing data set collected by the automatic monitoring system of an ice observation station of Sichuan Electric Power Exploration and Design Institute，the effectiveness of the prediction model is verified.Compared with the non optimized and the same type of prediction methods，the average mean square error of prediction is reduced by about 28%，21% and 3% respectively，and the prediction accuracy is improved to a certain extent.

Key words：power transmission line; automatic monitoring; icing prediction; principal component analysis; support vector regression machine

0?引言

輸電線路覆冰的增加會使導（地）線、絕緣子串以及桿塔的機械荷載增大，進而導致線路受到扭曲等機械力的破壞，將嚴重威脅電網的安全穩定運行［1］.國家電網信息化規劃明確要求加快電網智能化轉型，研究災害預警典型算法模型，對于海量數據有效災害預警信息的提取和整合具有不可忽視的意義［2］.

國內外大量專家學者對覆冰預測模型已開展了廣泛的研究，主要基于兩個大方向：一是，基于導線覆冰生長物理特性的預測模型；二是，基于覆冰發展相關因素的回歸預測模型［3-5］.對覆冰過程物理模型的研究主要集中在對導線結冰過程中凍雨與導線的碰撞流體力學規律研究與對空氣中水滴凍結系數的熱平衡過程研究［6］，如Goodwin模型、Makkonen模型等［7，8］.由于覆冰的生長過程很難基于某個確定的物理模型，實際覆冰預報的準確率仍有待進一步提升.

基于覆冰生長相關聯因素的擬合預測模型是依據可觀測和可預報的微氣象數據，利用機器學習算法建立的冰厚預測模型.如文獻［9］提出了采用多變量灰色預測模型，預測值平均相對誤差為6.69%，但此模型只適用于覆冰指數增長的預測，與實際值還有較大的偏差.文獻［10］提出一種基于自適應變異粒子群算法優化BP神經網絡的人工智能預測模型，相對誤差在30%以內，此模型的缺點是需要訓練較大的原始數據集來保證預測精度，對微氣象條件復雜多變的覆冰預測，結果差強人意.文獻［11］提出了一種基于遺傳算法與模糊邏輯融合的預測模型，隨著覆冰厚度的增加，模型預測的誤差會越來越大，并且忽略了數據集中屬性之間的相關性.文獻［12］提出優化多核相關向量機組合預測模型，在覆冰穩定期平均均方根誤差為12.1%.但目前的智能模型很少考慮線路覆冰的累積過程，導致預測值與實際值仍存在差距.

針對以上輸電線路覆冰預測誤差大、效率低、實用性較差等問題，本文運用理論基礎較為完善，且適用于小樣本數據擬合的支持向量回歸機（Support Vector Regression Machine，SVRM）智能預測模型.模型首先采用主成分分析法（Principal Component Analysis，PCA）提取影響線路覆冰的主要微氣象特征，考慮特征之間的相關性，去除噪聲和關聯性較強的信息.其次利用粒子群（Particle Swarm optimization，PSO）算法對預測模型參數進行尋優，建立覆冰預測模型.最后以四川電力勘探設計院某觀冰站采集的現場在線監測數據集，模擬導線拉力對所建立模型進行準確性驗證，同時為智能學習模型在線路覆冰預測領域與工程實踐中的應用提供參考.

1?預測模型理論

1.1?主成分分析

式（1）中：n表示輸入特征的個數，m為每個特征包含的原始變量個數.主成分分析法實現步驟如下：

首先，為了簡化計算并消除不同變量之間量綱的影響［13］，對所有輸入特征進行零均值規范化，將原數據轉換為符合均值為0，標準差為1的標準正態分布的新矩陣.規范化后的矩陣X*可表示為：

2?覆冰厚度預測模型建立

建立輸電線路覆冰厚度預測模型的關鍵是尋找覆冰現場自動監測系統采集到的氣象數據集與覆冰厚度之間的非線性映射關系，依據此關系對冰厚進行回歸分析，從而實現對短時期內線路覆冰厚度的預測.圖1為基于PCA-PSO-SVRM的覆冰厚度預測模型建立流程圖.

2.1?特征預處理

輸電線路覆冰現場監測的數據受設備所處環境與數據遠距離傳輸等影響雜質與噪音太大，無法直接進行數據挖掘或者數據應用，本文考慮影響導線覆冰的氣象因素依據環境溫度、相對濕度、綜合風速、綜合風向、氣壓、光輻射強度等建立覆冰預測模型.為了提高對數據提取與挖掘的質量，需要對原始數據集進行數據篩選［20］.線路覆冰的必要氣象條件為：環境溫度在0 ℃以下；空氣相對濕度一般在85%～90%以上；風速大于1.0 m/s；且當風向與線路正交時，最有利于覆冰厚度的增長.根據以上基本條件可以剔除實際測量數據中的不符合覆冰條件的數據.其次刪除數據集中的缺失數據、某特征持續12小時以上不變的數據等.以此達到對原始樣本數據得清理，以便對樣本進行主成分分析.

2.2?構建支持向量回歸機預測模型

融合樣本信息，構建SVRM覆冰厚度預測模型的步驟如下：

步驟1?模型初始化

將提取特征后的新數據作為覆冰預測模型的輸入，70%作為模型訓練集，30%作為測試集.其次初始化預測模型與粒子群優化參數，具體參數設置如表1所示.

步驟2?粒子群算法尋優

PSO算法于非線性、多峰值問題都著有較強的全局搜索能力.采用粒子群算法對參數C和g進行尋優，首先計算待優化粒子的最佳適應度值，其次更新迭代粒子的位置與速度，最后循環以上過程直至迭代次數達到上限，并將尋得的最優值輸入到預測模型中參與模型的訓練.

步驟3?模型訓練與評估

將訓練集數據輸入SVRM模型對預測模型進行訓練，測試集數據經過完全一致的數據處理過程對訓練完備的模型進行精度測試與驗證分析.本文選取均方根誤差eRMSE與平均絕對誤差eMAE兩個指標來對預測模型進行誤差分析，并對比其他預測模型預測準確度有所提高，兩個評估指標分別可表示為：

3?實例分析

3.1?數據來源與特征選擇

本文在線監測數據來源于四川某山區為長期積累區域覆冰基礎數據而設立的自動監測站.覆冰厚度是根據導線規格與拉力數據計算的導線等值覆冰厚度.在線監測樣本采集2022年1月28日至2022年2月24日每隔10 min共計2 234組氣象數據，圖2為觀冰站覆冰現場監測數據.

利用相關性分析去研究等值冰厚分別和光輻射強度、綜合風向、綜合風速、氣壓、相對濕度、環境溫度、導線拉力共7項特征與覆冰厚度之間的相關關系，使用相關聯系數去反映特征與覆冰厚度相關關系的強弱情況.

由表2可知，與覆冰厚度相關性最大的兩個微氣象特征是環境溫度和環境相對濕度，其他特征的相關度均小于0.5.

對輸入特征進行進一步主成分分析，根據圖3的現場監測數據，對輸入特征使用主成分分析法進行信息濃縮，數據集的適合主成分分析系數為0.720，大于0.6，意味著數據可用于主成分分析研究.

由圖3顯示的微氣象特征的累積對覆冰厚度的方差解釋率可得，前兩項輸入特征的累積對覆冰厚度的影響已經達到77.428%，因此主成分分析法將輸入特征進行壓縮，提取主要信息量進行分析.

3.2?參數尋優

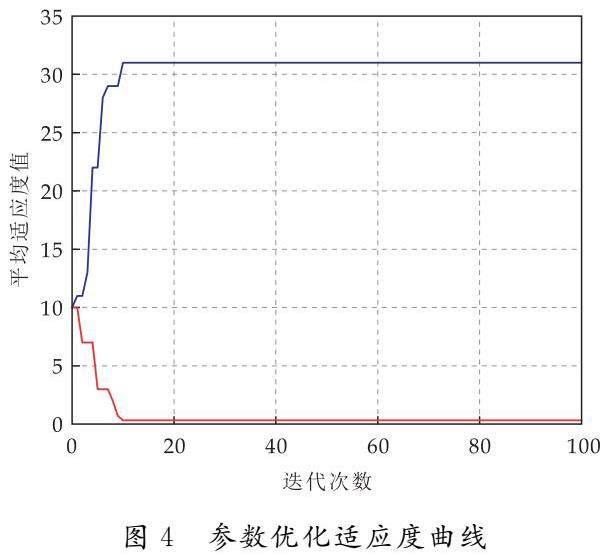
在對SVRM模型進行訓練之前，對模型中影響預測精度的兩個主要參數進行迭代優化，參數平均適應度值曲線如圖4所示.由圖可知，粒子群算法在迭代10次就達到收斂，尋優速度快，說明粒子群算法對預測模型參數的優化起到了重要作用，經過優化后的最優懲罰系數C=31.883，核函數參數g=0.3，將這兩個參數值賦予支持向量機預測模型對覆冰厚度進行預測.

3.3?預測結果分析

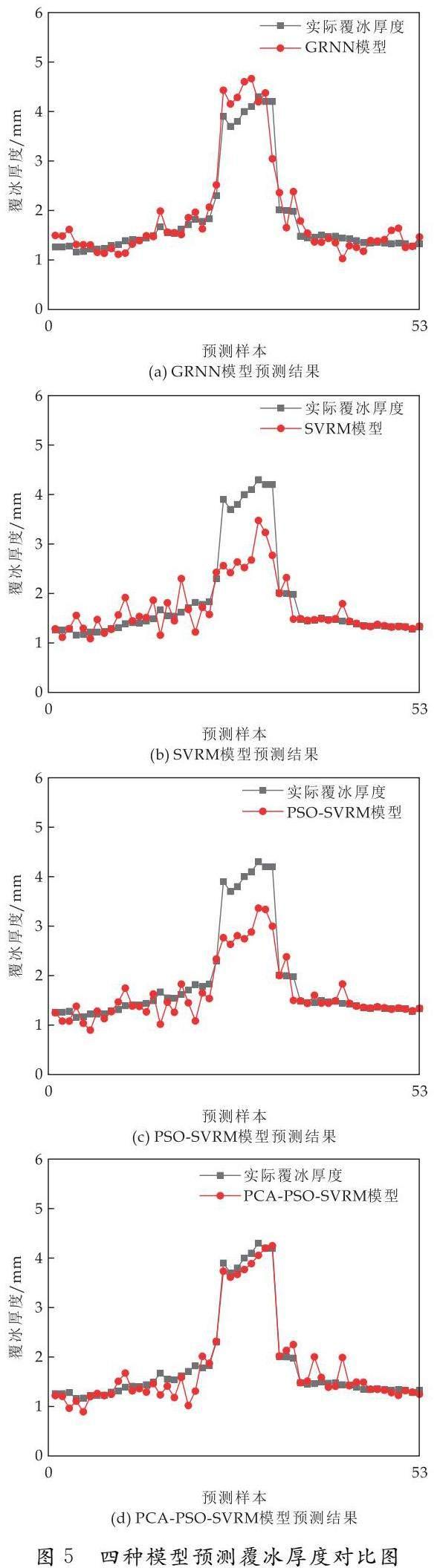
為了直觀地分析本文提出的預測模型，現對53個測試樣本進行預測分析.將未優化的SVRM模型、未進行性相關性分析的PSO-SVRM模型、常用于隨著樣本數量增加預測效果越優越的的傳統GRNN模型與本文所提出的優化SVRM模型覆冰厚度預測結果進行對比，如圖5所示為四種模型預測覆冰厚度對比圖.由預測結果可知隨著時間的變化與預測樣本數的增加，本文所提出的預測模型無論是在覆冰增長期、覆冰穩定期還是覆冰消融期預測結果均與實際覆冰值最相近，最準確跟隨了實際覆冰厚度發展趨勢.

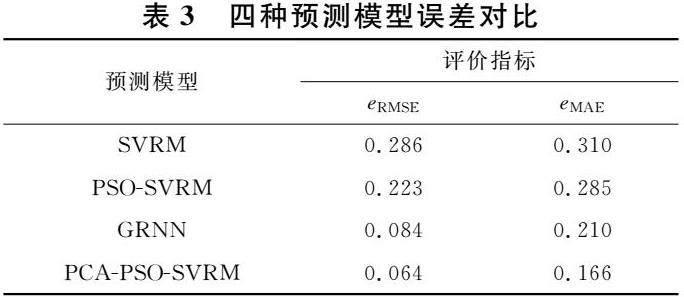
為驗證本文預測模型的低誤差率，對四種模型進行進一步誤差評估.如表3所示，對四種模型預測均方根誤差eRMSE與平均絕對誤差eMAE兩個指標進行對比.與SVRM模型、PSO-SVRM模型、GRNN模型相比，本文預測模型平均均方誤差eRMSE分別減少了約28%、21%、3%，平均絕對誤差eMAE分別減少了約14%、11%、4%，預測準確度有一定的提高，進一步體現了本文所提出的預測模型的預測能力與可靠性.

綜上所述，因微氣象條件的復雜多變與數據獲取不易等特征，此文提出的這種針對小樣本數據集的預測模型，適合根據可短期預報的微氣象數據對輸電線路覆冰進行預測，且有可觀的現實應用意義.

4?結論

本文提出了一種優化SVRM的輸電線路覆冰厚度短期預測模型，為線路覆冰厚度預測提供了一種切實可行的方法.首先運用主成分分析法對影響輸電線路覆冰厚度的氣象特征進行了主成分提取與信息濃縮，從而減少了預測模型的輸入數據復雜度.其次提出了改進SVRM預測模型，利用粒子群算法對影響預測模型預測精度并且難以取值的兩個重要參數進行迭代尋優，將尋得的最優值賦予預測模型對覆冰厚度進行高效預測.最后實驗驗證對比未優化與傳統神經網絡預測模型在覆冰增長期、平穩期、消融期預測精度都有一定的提高.將此模型利用于覆冰現場對電力設備的調度、人力與信息資源的合理分配等方面才能顯現出此預測技術的現實價值.

參考文獻

［1］ 黃新波，劉家兵，蔡?偉，等．電力架空線路覆冰雪的國內外研究現狀［J］.電網技術，2008，32（4）：23-28.

［2］ 莊文兵，祁?創，王?建，等．基于微氣象監測的輸電線路覆冰動態過程估計模型［J］．電力系統保護與控制，2019，47（14）：87-94.

［3］ Farzaneh M，Savadjiev K.Statistical analysis of field data for precipitation icing accretion on overhead power lines［J］.IEEE Transactions on Power Delivery，2005，20（2）：1 080-1 087.

［4］ 陳雨鴿，高?偉，林鴻偉，等.一種基于長短期記憶網絡的線路覆冰預測模型研究［J］.電工電氣，2020（3）：5-11.

［5］ Zarnani A，Musilek P，Shi X，et al.Learning to predict ice accretion on electric power lines［J］.Eng.Appl.Artif.Intel.，2012，25（3）：609-617.

［6］ Farzaneh M.Atmospheric icing of power networks ［M］.Berlin：Springer，2008.

［7］ 邸悅倫，陸佳政，徐勛建，等．2016年“超級寒潮”條件下湖南電網覆冰過程的分析［J］．電力科學與技術學報，2019，34（2）：187-194.

［8］ 羅?聰，范力棟，趙學文，等．基于VMD-IGWO-LSSVM的覆冰預測模型研究［J］．電網與清潔能源，2021，37（6）：9-17.

［9］ 劉宏偉，陸佳政，賴旬陽，等．輸電線路覆冰厚度短期多變量灰色預測模型研究［J］．高電壓技術，2015，41（10）：3 372-3 377.

［10］ 李賢初，張?翕，劉?杰，等．輸電線路導線覆冰AMPSO-BP神經網絡預測模型［J］．電力建設，2021，42（9）：140-146.

［11］ 黃新波，王玉鑫，朱永燦，等．基于遺傳算法與模糊邏輯融合的線路覆冰預測［J］．高電壓技術，2016，42（4）：1 228-1 235.

［12］ 熊?瑋，徐?浩，徐林享，等．計及時間累積效應的RF-APJA-MKRVM輸電線路覆冰組合預測模型［J］．高電壓技術，2022，48（3）：948-957.

［13］ 戴?棟，黃筱婷，代?洲，等．基于支持向量機的輸電線路覆冰回歸模型［J］．高電壓技術，2013，39（11）：2 822-2 828.

［14］ 林海明，杜子芳．主成分分析綜合評價應該注意的問題［J］．統計研究，2013，30（8）：25-31.

［15］ 韓小孩，張耀輝，孫福軍，等.基于主成分分析的指標權重確定方法［J］．四川兵工學報，2012，33（10）：124-126.

［16］ Kumar M A，Gopal M.Least squares twin support vector machines for pattern classification＼[J＼].Expert Systems with Applications，2009，36（4）：7 535-7 543.

［17］ 楊俊燕，張優云，朱永生.ε不敏感損失函數支持向量機分類性能研究［J］.西安交通大學學報，2007，41（11）：1 315-1 320.

［18］ Christopher Bishop.Pattern recognition and machine learning［M］.New York：Springer，2007：325-357.

［19］ 劉?健.基于支持向量機的在線學習算法研究［D］.杭州：浙江大學，2013.

［20］ 黃宵寧，許?瑞，許家浩.南方山區線路覆冰在線監測數據特征分析與預測模型研究［J］.電力系統保護與控制，2015，43（23）：111-116.

【責任編輯：蔣亞儒】

基金項目：國家自然科學基金項目（62073206）；陜西省科技廳科學技術研究發展計劃項目（2018GY-031）

作者簡介：湯?偉（1971—），男，河南信陽人，教授，博士生導師，研究方向：工業過程高級控制理論、光機電一體化控制系統