算法總在算理后
杜永寧
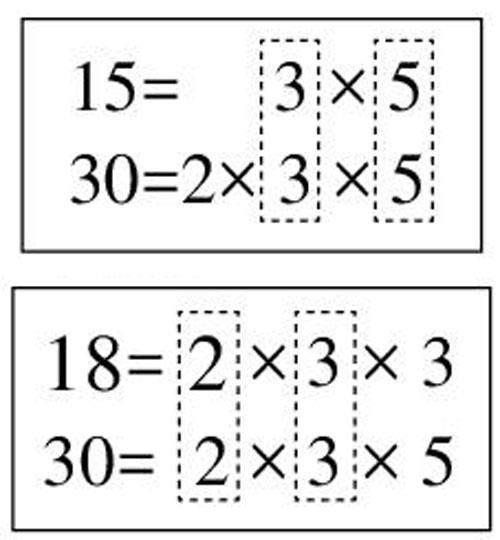
【問題】怎樣求兩個數的最小公倍數?為什么這樣做?
【困惑】通常這樣處理上述問題的教學,以西南師大版五下教材為例進行說明。
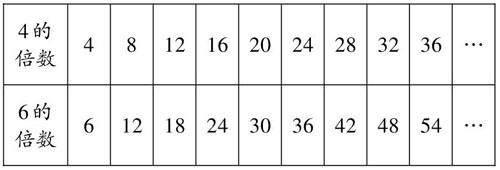
1.分別列舉4的倍數和6的倍數,如下表
2.你發現了什么?
預設:4和6的倍數都有無數個;
4和6的倍數中有相同的數;
12,24,36,……既是4的倍數又是6的倍數……
3.講解:什么是公倍數,什么是最小公倍數?
4.提出問題:除了這樣的列舉法,你還能怎樣找出兩個數的最小公倍數?
學生自主探究
5.匯報(教師一般借助已經通過其他途徑學會的學生講解,學習怎樣用短除法求兩個的最小公倍數)
6.練習并發現求兩個數最小公倍數的規律
……
上面的教學過程看起來以學生為主體,順利完成了求最小公倍數的教學。但實際教學中,發現采用這種灌輸式的教學方法,學生對于為什么可以用短除法這樣來求兩個數的最小公倍數沒有真正理解。這也是教師的困惑所在,怎樣才能讓學生真正理解求兩個數最小公倍數的算理呢?
【思考】
1.找準新知識的生長點。求最小公倍數應該在什么知識上生長起來?倍數、公倍數和合數的改寫(分解質因數)。所以,講解完公倍數和最小公倍數后,可以提問:4和6的公倍數24與4和6有什么關系?為什么24卻不是4和6的最小公倍數呢?
(1)4×6=24,24既是4的倍數,又是6的倍數,所以24是4和6的公倍數。
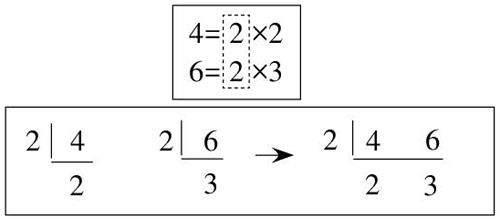
(2)為什么24卻不是4和6的最小公倍數呢?學生要發現原因,不會那么容易,所以課前可以鋪墊把4和6用短除法改寫成質數相乘的形式4=2×2,6=2×3,學生觀察分解式推測、發現:4×6時,它們公有的質因數2乘了2次,如果只乘1次,剛好是最小公倍數12。也就是說,兩個數的乘積一定是這兩個數的公倍數,但不一定是它們的最小公倍數,要求最小公倍數還需要……
2.自主構建方法。通過上面的發現,求兩個數最小公倍數的方法呼之欲出,追問:你認為可以怎樣求出兩個數(4和6)的最小公倍數?
(1)分解篩選相乘法。雖然4×6,即2×2×2×3是它們的公倍數,但因為4和6有公有的質因數2,所以這個2只取一個,4和6的最小公倍數就是2×2×3=12。
(2)短除法。能不能把上面的分解寫成短除法呢?兩個短除法能合并在一起嗎?我們發現,4和6公有的質因數2在短除法里只寫了一次,所以直接把所有的除數和商乘起來就是4和6的最小公倍數,即2×2×3=12。
對比兩種方法,它們本質上是相同的,只是寫法不同而已,短除法直接把公有的質因數篩選出來了,更簡潔。
我們注意到,在理解求兩個數的最小公倍數算理的教學中,“4×6=24”這個算式發揮了重要作用,而它正是原始概念“倍數”定義的基礎。
3.借助算理,掌握規律,拓展方法。理解了求兩個數最小公倍數的算理,就可以進一步掌握求最小公倍數的規律,實現方法的優化和拓展。
(1)利用規律直接得到最小公倍數。 [15,30]=3×5×2=30,即有倍數關系兩數的最小公倍數是較大數。
4和7沒有公有質因數,不存在篩選,所以[4,7]=4×7=28。
(2)大數擴倍法。[18,30]= 2×3×5×3=30×3=90,顯然兩個數的公倍數一定是較大數的倍數,所以可以直接把大數拿來擴倍,從擴大到原來的2倍開始,只要得數也是較小數的倍數時,即可求得兩數的最小公倍數。
(3)縮小乘積法。例如,18×30=540,540一定是18和30的公倍數,如果把540除以18和30公有的質因數2和3同樣可以求到它們的最小公倍數,這種方法沒有現實意義,只是算理上的存在而已。
這樣的教學,學生在深刻理解算理的基礎上,也就自然能掌握求兩個數最小公倍數的算法,并體會各種算法之間的聯系,真正內化這一重要的基本技能。因此,我們有理由說,精彩的算法總在深刻的算理之后。

