車用雙層微通道散熱器熱性能的優化研究

張永棟，蔣翠翠，鄭少鵬

（廣東交通職業技術學院 汽車與工程機械學院，廣東 廣州 510640）

隨著純電動汽車芯片性能的快速提高，散熱不足已成為電子技術發展的瓶頸。當熱流密度超過100 W/cm2時，傳統空氣冷卻技術無法滿足散熱需求，取而代之的是液體冷卻技術[1]。在高通量液冷散熱裝置中，微通道散熱器（Micro-channel Heat Sink, MHS）因為具有較大的傳熱面積與體積比，被認為是改善散熱性能的最佳方法之一[2]。微通道散熱器作為一種高性能散熱裝置，可以承受高達790 W/cm2的熱通量，極大地提高超高速超大規模集成電路的可行性[3]。文獻[4-5]提出了雙層微通道散熱器（Double Micro-channel Heat Sink,DMHS）的概念，進一步提升微通道散熱器的散熱性能，并降低所需的壓降和泵送功率。為使雙層微通道散熱器達到更好的整體熱性能，本文在一定的約束條件下，以最小熱阻為目標，利用響應曲面法對結構進行了優化設計，獲得了良好的效果。

1 雙層微通道散熱器整體結構

硅基微通道散熱器在汽車芯片領域應用廣泛。因此，本文選擇硅作為散熱器基本材料。冷卻液選擇去離子水（初始溫度為300 K），因其優越的物理和熱力學性能而被廣泛選為冷卻劑。雙層微通道散熱器如圖1 所示，散熱器由矩形鰭片組成，整體高度包括上下層通道高度、頂板厚度、中間板厚度和基板厚度組成，整體寬度12 mm，長度15 mm，原始尺寸如表1 所示。熱源布置在散熱器下方，兩者緊密連接，不考慮熱阻影響，上下層流體流動方向相同。

表1 兩種原尺寸雙層微通道散熱器結構參數 單位：μm

圖1 雙層微通道散熱器結構

圖1 中，Wc,u、Wr,u、Hc,u、Wc,l、Wr,l、Hc,l分別是雙層微通道散熱器上層通道寬度、上層鰭片厚度、上層高度，下層通道寬度、下層鰭片厚度、下層高度；H為散熱器整體高度，δu為頂板厚度，δm為中間板厚度，δb為基板厚度。

2 研究方法

由于雙層微通道散熱器結構參數與熱性能間不存在明確的函數關系，所以本文引入響應曲面法（Response Surface Methodology, RSM），建立熱性能參數與結構參數間的回歸模型，通過對回歸模型的優化得到最佳結果。

RSM 是數學、實驗設計和統計分析相結合的方法，該技術利用合理的實驗設計，找出對結果有顯著響應的參數，并采用多元二次回歸方程建立自變量和因變量之間的數學模型，通過對回歸方程的分析尋找最優結構參數。RAHIMI-GORJI等人[6]采用RSM 對單層微通道散熱器通道幾何結構進行優化設計，取得了良好的效果，證明RSM在微通道散熱器結構優化的有效性。ZHOU 等人[7]也采用RSM 結合有限體積法對一種呈正弦波結構微通道的幾何參數進行了優化，發現該方法具有高效、準確的特點，對非規則傳熱結構的優化具有廣泛的應用前景。

實踐證明使用RSM 可以減少解決目標所需的時間，并節省大量資源。本文使用計算流體力學（Computational Fluid Dynamics, CFD）軟件代替實驗，結合CFD 優化雙層微通道結構。文中采用二階模型，即響應因變量y包含線性項、平方項和叉積項三部分，定義為[8]

式中，xi、xj為設計變量，本文中設計變量為雙層散熱器結構參數，a是調諧參數，下標i代表響應觀測中的觀測單位，n是變量的數量。

大量研究表明，微通道散熱器在實際工程應用更加看重泵功率和熱阻的關系，微通道散熱器泵工定義為

式中，P為微通道散熱器泵功；A為散熱器通道截面積；Δp為散熱器壓降損失。

總熱阻定義為

式中，Tw,max為底板的最高溫度；Tin為冷卻液入口溫度；Ab為計算域的底板面積，熱通量為恒定值：qw=2×106W/m2。

3 優化方案

本文采用數值模擬結合曲面響應方法開展研究，為了簡化模型和網格數量，節約計算時間，考慮到圖1 所示的周期性和對稱性條件，根據雙層微通道散熱器的結構特征，提取一個對稱單元尺寸作為計算域單元尺寸為（0.24×0.95×27）mm，頂板、基板、中間隔板厚度為50 μm，散熱器上下層具有固定的鰭片間距，分別為80 μm、120 μm，上下層通道總高度為800 μm，以冷卻液入口流速、下層通道寬度、上層通道寬度和下層通道高度為變量，以在泵功率等于1.2 W 時最小熱阻為目標，變量及變量尺寸變動范圍如表2 所示。

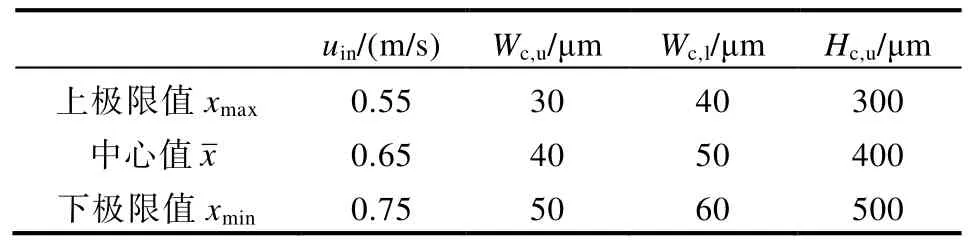
表2 散熱器結構變量與變量尺寸變動范圍

表2 中，uin為入口流速；Wc,u為下層通道寬度；Wc,l為上層通道寬度；Hc,u為下層通道高度。

為了便于計算，利用式（4）進行歸一化，得到歸一化的變量如表3 所示。

表3 變量與變量尺寸變動范圍（歸一化后）

式中，Z為歸一化后的無量綱變量；Δx為設計變量取值范圍的中心值即

中心復合設計是最常用的響應曲面法的試驗設計方法，可以具體高效估計一階和二階項，從而評估因子的非線性影響。中心復合設計適用于多因素多水平實驗，有連續變量存在的場景，中心復合設計能更好地擬合相應曲面。本研究利用中心復合法設計實驗方案并得到結果，表4 列出了實驗設計方案矩陣以及獲得的熱阻Rth和泵浦功率P結果。

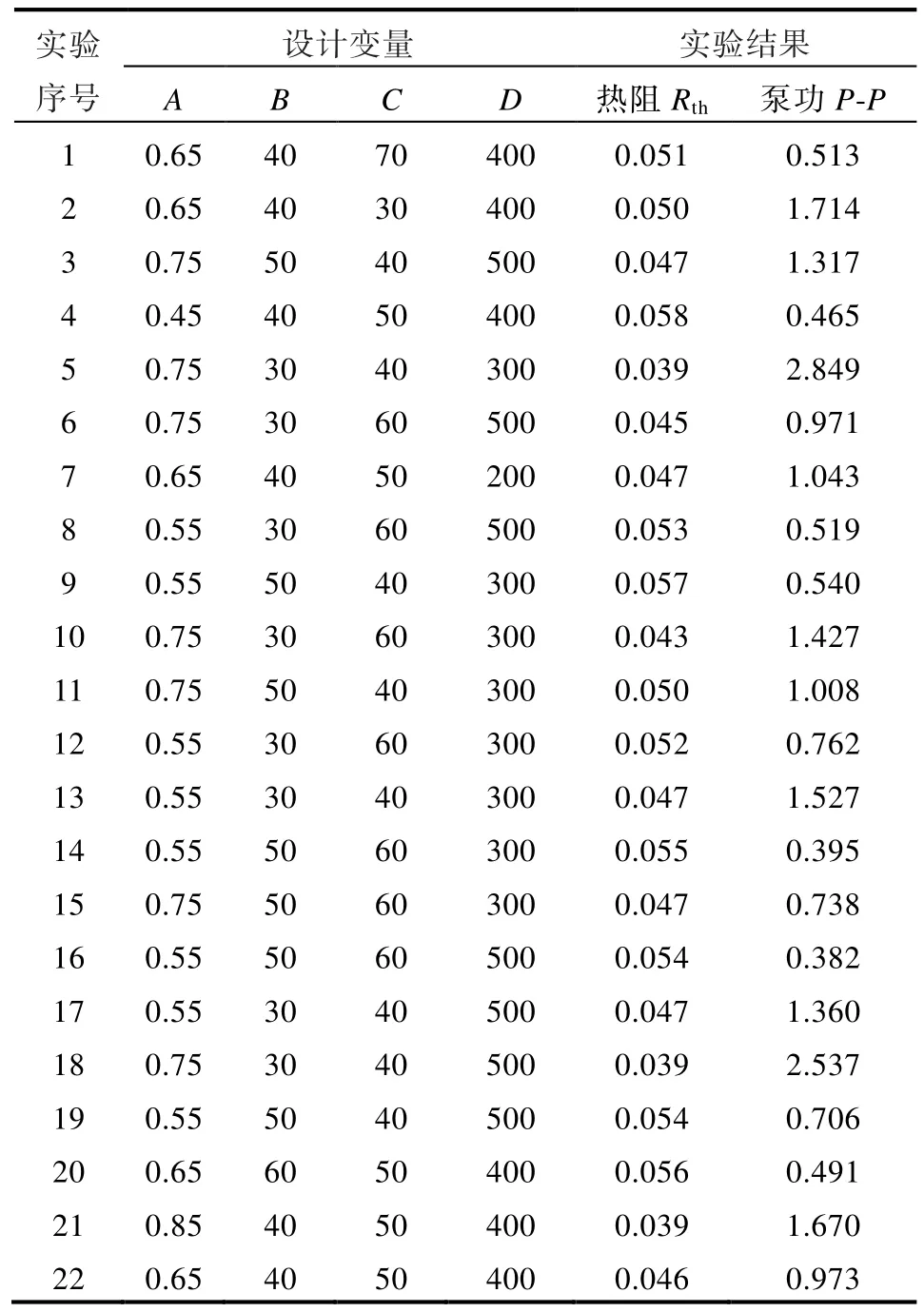
表4 實驗設計矩陣和結果

表5 以方差分析的形式給出了熱阻二次模型的結果。表5 中，“Model”項的P值為0.00，小于0.05（即a=0.01，或95%置信度時），這表明模型可信度高，可以認為具有統計意義，證明模型中的項對響應有顯著影響。詳細分析每一個模型項的影響，可以看出，因子A、因子B、因子C的主效應，二次項A×A、B×B、C×C以及因子B與因子C、因子B與因子D的交互效應是顯著。盡管因子D的主效應不顯著，但因子B與因子D的交互效應是顯著，因此，擬合過程保留因子D的主效應項。因子C與因子D的交互效應F值小，P值趨近于0.05，因此忽略因子C與因子D的交互作用，其他項由于其P值大于0.05，可被視為不顯著影響。

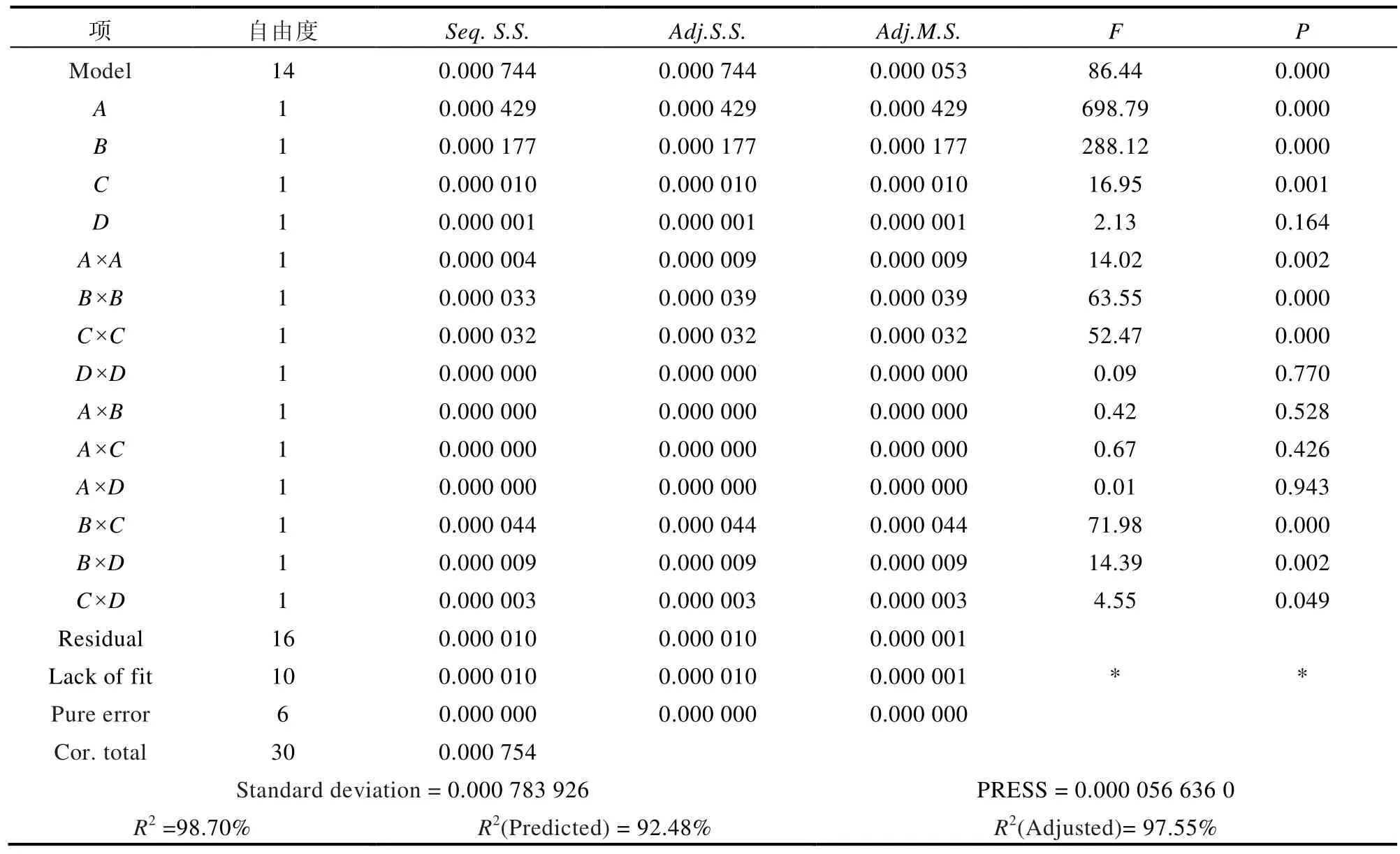
表5 熱阻的方差分析表（不顯著項消除前）

根據表5 的方差分析結果，刪除D×D、A×B、A×C、A×D、C×D等不顯著項，重新進行擬合，得到如表6 所示結果。表6 中“Model”的P值亦為0.00，證明模型具有顯著的統計學意義，即模型中的各項對響應有顯著影響。

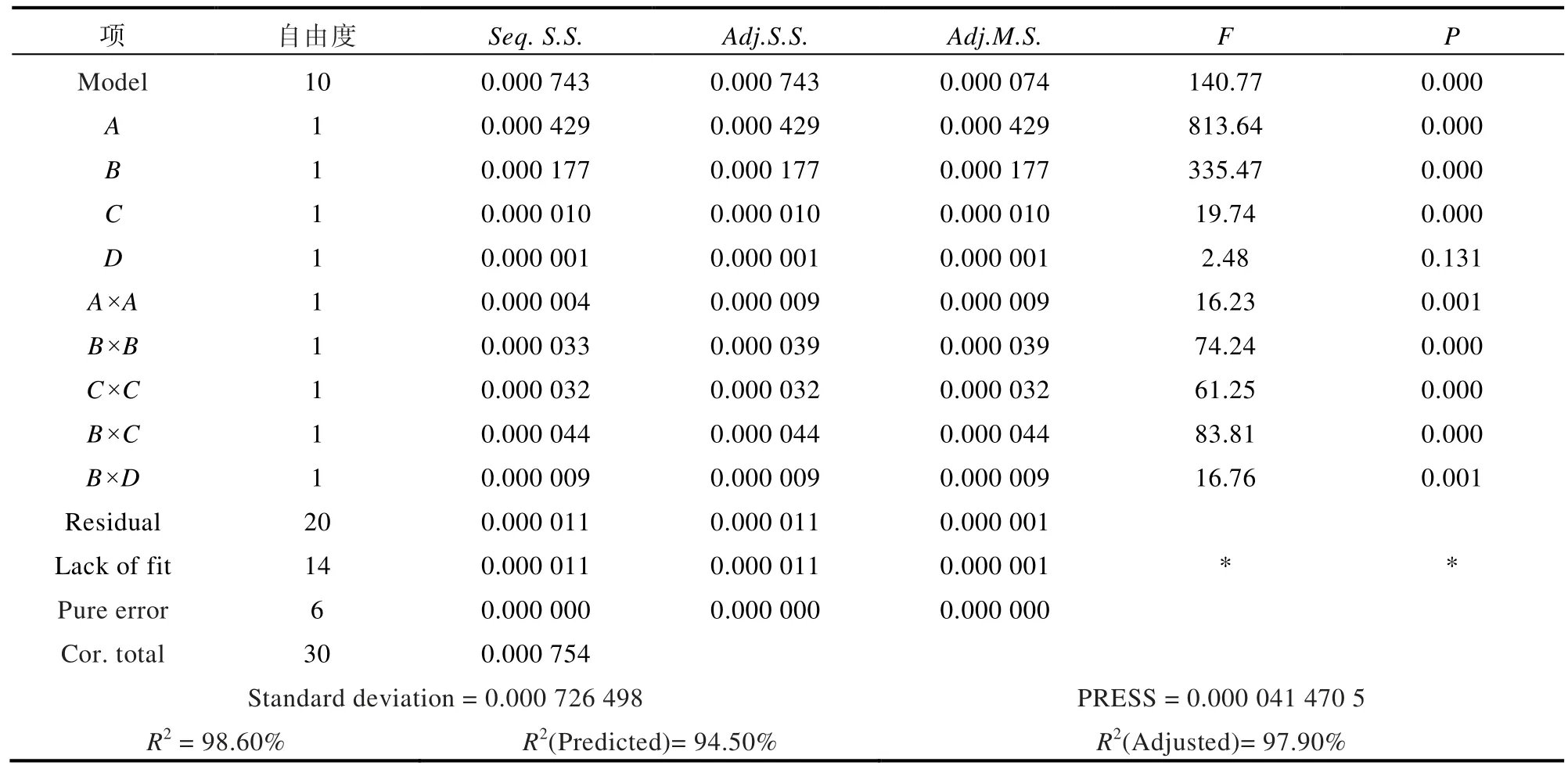
表6 熱阻的方差分析表（不顯著項消除后）

由表6 可以得到熱阻的二次回歸方程：

同樣的方法分析得到泵功二次回歸方程：

本研究以泵功及空間大小為設計限制條件，對雙層微通道散熱器進行優化，目的是尋找最佳的設計約束值，根據上述分析最終形成優化的數學模型：

約束條件：

利用MATLAB 的fmincon 函數求解約束非線性規劃，取整并經過逆歸一化處理后得到雙層微通道散熱器的結構尺寸如表7 所示。

表7 優化后的新型散熱器幾何參數 單位：μm

4 結果與討論

通過曲面響應法建立的回歸方程顯示了下層通道高度Hc,l、上層通道寬度Wc,u和下層通道寬度Wc,l三個因子對泵工和熱阻的影響，可以看出，Hc,l主效應對熱阻和泵工都不顯著，而是與上層通道寬度之間有著顯著的交互效應。Wc,u和Wc,l兩個因子對響應影響顯著，通過系數的正負可以很明顯看出兩個因子對熱阻和泵工起著相反作用。對于泵工，Wc,u系數是Wc,l的四倍多；對于熱阻，兩者的系數差距不大。因此，通過減少Wc,u來降低熱阻結合，增加Wc,l來控制泵工的方式來改善整體性能。圖2 展示了優化后的散熱器方案DMHSOP 在0.55 m/s、0.65 m/s、0.75 m/s、0.85 m/s、0.95 m/s和1.1 m/s 六個指定的入口速度時，泵功率與總熱阻的關系，并與其他兩種原尺寸DMHS-1、DMHS-2 做對比。可以看出，經過優化后，相同泵工時，熱阻都有了下降，在泵工為1.2 W 時，與DMHS-1、DMHS-2 相比分布下降了9.42%、4.23%，證明了RSM 的有效性。

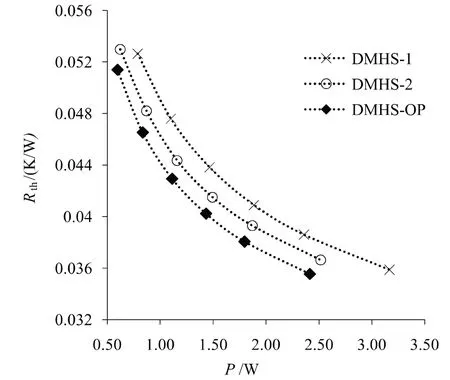
圖2 泵功率與總熱阻的關系對比

5 結論

本文對一種雙層微通道散熱器進行了優化研究，并與原始尺寸的雙層微通道散熱器進行了比較研究，針對響應和因子沒有確切關系的情況，利用RSM 是一種比較合適的優化方法。通過RSM可以發現不同因子對響應的影響程度，同時可以看到不同因子間的交互效應。通過優化，改變上下層結構，增加下層鰭片厚度和通道寬度，可以逼迫更多流體流向下層通道，從而改善了流體的流動分布，整體性能得到進一步提升，比原始尺寸的雙層微通道散熱器熱阻分別降低4.23%、9.42%。