基于蟻群算法的生鮮電商冷鏈低碳配送路徑優化研究

李艷珍

(黎明職業大學，福建 泉州 362000）

一、研究背景及研究現狀

（一）研究背景

近年來，電子支付的便捷、物流體系的完善、大數據的算法支持及移動購物的普及，有效地提高生鮮行業供給的質量，同時消費升級帶動生鮮的需求旺盛。2021 年，中國生鮮電商完成3117.40億元的市場交易份額，實現跨越式的擴張，占比同期上升18.2%。基于近幾年消費者需求量增量比上升的情況，生鮮電商行業報告預計2023 年中國生鮮電商市場規模將達4198.30 億元。[1]由于生鮮食品保質期短、易腐爛等特點，全程需要冷鏈配送，因此冷鏈物流將是一個巨大的市場。減少貨損和保持新鮮是冷鏈物流的重要特征，在配送過程中對時間、環境等要求苛刻，加之人們對生鮮品質、配送服務的消費升級，使冷鏈物流配送備受關注。[2]在“30·60 雙碳”目標下，交通運輸與物流產業需要加速綠色、低碳轉型之路。據統計，交通物流行業占全球二氧化碳排放量的21%，道路碳排放占整個運輸部門碳排放量的70%。[3]王雁鳳和黃有方[4]指出，預計到2050年物流運輸行業的碳排放比2007 年將增加150%-250%。冷鏈物流是物流行業的高耗能、高碳排放業務。因此，在“雙碳”目標下，如何加強冷鏈配送節能減排的路徑設計和系統規劃，在考慮經濟成本的同時也要關注環境目標，成為冷鏈配送的研究重點。

（二）國內外研究現狀

冷鏈物流的路徑優化一直是物流領域的研究重點，最早的路徑優化問題（Vehicle Routing Problems，VRP）研究自1959 年由Dantzig 和Rams?er[5]提出以來，引起了學術界的廣泛關注。針對路徑優化問題，學者們提出一系列優秀的精確算法，其中蟻群算法（Ant Colony Algorithm，ACA）被廣泛應用。Zmazek.B[6]提出一種在汽車行駛和動力極限問題上增加了時間窗（CVRPTW）的優化算法，并且在一天之內進行多次往返，最后以實例說明該方法的正確性。Vijay Aggarwal[7]提出一種決定系統，用以確定合適的節點和價值來決定運輸費用，并決定與結點數目相關的運輸網絡。Monitarian[8]利用數學方法，解決冷鏈配送次序問題，從而提高配送決策的科學性。國內學者對冷鏈物流路徑優化研究也取得了重要成果。Mei-xian Song 等[9]提出一種改進的人工魚群算法以考慮不同類型車輛的問題特征，該算法嵌入右移啟發式算法，在不增加能耗的情況下提高用戶滿意度。樊世清等[10]以總成本最小為目標建立農產品冷鏈物流車輛配送路徑優化模型，采用改進的蟻群算法進行求解得到最優方案。康凱等[11]采用局部搜索機制在算法中融入2-opt 局部優化方法，實現了對蟻群算法的改進。

隨著節能減排成為全球關注的熱點，越來越多的學者在研究冷鏈配送路徑優化時也關注綠色目標的實現。王雁鳳等[12]利用構建的港口群運輸網絡優化模型對25 種場景下的運輸路徑進行計算，得出最優的配置方案。周鮮成等[13]分析行駛時間和時變速度的關系，提出一種基于路段劃分的行駛時間計算方法，采用MEET 模型測度碳排放，以車輛使用成本、駕駛員成本、油耗成本和碳排放成本構成的總成本作為目標函數構建時間依賴型GVRPTW 模型。Li-Yi Zhang 等[14]將低碳經濟引入冷鏈物流，并與蟻群算法優化相結合。Yongbo Li 等[15]采用創新的方法更新信息素開發了改進后的蟻群算法，為多站點綠色低碳車輛路徑問題提供更好的解決方案。范立南等[16]建立考慮碳排放的路徑優化模型，并采用改進遺傳算法對路徑進行優化。

綜上所述，對于冷鏈物流車輛配送路徑問題，國內外學者已經進行了較為廣泛的研究，但是在現存數學模型中，對懲罰成本、碳排成本等實際影響要素考慮不全的問題仍然存在，且蟻群算法初始信息素少、收斂速度慢的缺點仍未得到較有實用性的優化處理。以綜合成本最小化作為優化目標，既考慮環境效益也考慮經濟效益，將懲罰成本、碳排放成本引入模型參數中，再采用改進信息素更新方式和揮發量調整優化蟻群算法，結合優化后的模型和算法，以上問題將得到有效處理。本文以泉州市某生鮮電商宅配中心作為實例進行數據試驗，解決其冷鏈末端物流成本高、響應速度慢和碳排量高的問題，有利于降低車輛配送成本、優化配送路徑、提高冷鏈末端響應速度，以增加整體效益。

二、生鮮電商冷鏈低碳配送路徑優化模型

（一）問題描述

本文探討的生鮮電商冷鏈低碳配送路徑優化問題具體可描述為：擁有m 臺配送車輛的某生鮮電商冷鏈物流配送中心，為n個具備生鮮產品需求的客戶提供冷鏈物流配送服務，n 個客戶的需求量和地理位置固定且每個客戶都有配送時間的限制，所有配送車輛統一從配送中心出發，完成配送服務后返回配送中心，在滿足客戶需求量、車輛載重量限制、配送時間條件下合理安排車輛，使目標函數最優化。在以綜合總成本最小為目標的模型構建中，將運輸成本、固定成本、貨損成本、制冷成本、碳排成本、懲罰成本作為主要影響因素，尋找以客戶需求、車輛載重、服務時間窗為約束的車輛配送最短路徑，以優化冷鏈物流車輛配送路徑。

（二）模型的假設條件與約束條件

1.假設條件

為了對該問題進行深入的研究，將問題轉化成具體模型，需要做一定的假設：

假設1：配送中心的貨物種類和貨物數量可以滿足客戶的要求。

假設2：由單一配送點向多個客戶提供配送服務。

假設3：配送過程中不考慮路況、天氣等影響，每臺車速度相同，配送完成后返回配送中心。

假設4：已知客戶的產品需求量、地理坐標、時間窗要求和服務時間。

假設5：冷鏈運輸的車輛都是相同型號的冷藏車，且在配送期間的運行速度一致。

假設6：各運輸車輛的起始點均為配送中心，并完成配送后再返回。

假設7：隨著剩余貨物被服務客戶點的需求量逐漸遞減，車輛在配送過程中貨物載重量隨之變化。

假設8：配送車輛提前到達和推遲到達的懲罰系數已知并相同。

2.約束條件

建立模型時，還需滿足以下的約束條件：

約束1：配送車輛的貨物重量≤車輛最大的裝載重量。

約束2：配送車輛均為包車運輸，不與其他企業的貨物放一起運輸。

約束3：在顧客同意的時間窗口內完成冷鏈運輸工作。

約束4：一輛冷藏運輸車對應多個客戶，貨物裝載時先配送的客戶后裝載。

約束5：每個客戶需求點對配送時間有時間窗要求，且事先設定與時間窗相聯系的懲罰時間系數。

（三）成本變量分析

根據問題描述和假設，在生鮮電商冷鏈車輛配送路徑問題上，本文綜合考慮冷鏈物流環節中各項成本，以總成本最小化為目標，總成本C由六個部分組成：固定成本C1、運輸成本C2、貨損成本C3、制冷成本C4、碳排成本C5、懲罰成本C6。

1.固定成本

固定成本C1：包括車輛的固定費用、月檢費、司機工資等。固定成本僅與配送車輛的數量成正比。

式(1)中，m 表示配送點車輛數量，Fk表示車輛k所耗費的固定成本(k=1,2,3,...m)。

2.運輸成本

運輸成本C2：指配送過程中車輛在一定運輸工作量內所分攤的油耗費用，一般與配送車輛的行駛里程成正比。

式(2)中，n 表示客戶的數量，Cij表示車輛從客戶i 到客戶j 單位距離的油耗費用，dij表示客戶i到客戶j 之間的距離，Xij為0-1 變量，Xij=1 表示第k 輛車從客戶點i駛向客戶點j，相反，Xij=0 表示第k輛車未從客戶點i駛向客戶j。

3.貨損成本

貨損成本C3：指產品在隨時間的變化而產生的損耗。

式(3)中，P1為產品單位價格，Qi為客戶i 的產品需求量，a 為產品變質率，t0i為從配送點到客戶點i的時間，yj為0-1變量，若車輛k為客戶j服務，yj=1，否則，yj=0。

4.制冷成本

制冷成本C4：指為滿足產品保溫要求購買制冷劑而產生的費用，由于制冷劑也存在時效性，則不考慮行駛時間，制冷成本僅與運量有關。

式(4)中，qij為車輛從客戶i 到客戶j 之間的運量，P2為配送過程中單位重量的制冷成本。

5.碳排成本

碳排放成本C5：是指配送過程中車輛消耗燃料所產生的CO2排放成本，碳排放量=燃料消耗量×CO2排放系數。[14]燃油消耗量既與運輸距離有關，也和車輛載重量有關。

式(5)中，E 為車輛單位距離的油耗，e 為CO2排放系數，Pc為單位碳稅價格。

6.懲罰成本

懲罰成本指車輛未能滿足客戶的服務時間窗要求而產生的賠付成本。處罰費與顧客接受服務的時間窗口有關，并對顧客的滿意程度產生一定的影響。在生鮮產品的運送中，應注意其配送的時間性，以確保商品在顧客手中的安全。[17]為此，提出了一種基于混合時窗的限制條件，該方法可以使配送車輛在最優配送時間前或在最優配送時間后抵達，但必須付出相應的處罰費用。但在超出顧客可以接受的時間窗口以外，配送車輛不得無限地抵達，否則將會導致交易失敗。懲罰函數用表示：

式（6）中：∞表示極大值；μ表示超過單位時間產生的成本；懲罰成本用C6表示：

（四）模型構建

綜上所述，構建的生鮮電商冷鏈物流配送路徑優化模型如下：

1.算法設計

蟻群算法是一種仿生智能算法，主要用于路徑優化模型的求解。[18]該算法具有正反饋機制、并行搜索性、自組織性和較強的魯棒性、易于與其他算法結合等優點。相較于其他算法，它在搜索效率和時間復雜度方面具有明顯優勢，故被采納用于模型求解。

（1）蟻群算法基本設置

在完成蟻群算法的數學建模之前，做出以下假設：第一，螞蟻不會在路上一遍又一遍地訪問同一個客戶；第二，螞蟻可以知曉客戶之間的距離，在其他條件相同的情況會傾向于前往最近的客戶。第三，螞蟻在行進過程中會釋放信息素，且傾向于選擇信息素濃度較高的方向行進。

（2）參數初始化

設螞蟻數量m，客戶數量n，客戶i 和客戶j 之間的距離為dij（i,j=1,2,...,n）；

t 時刻客戶i 和客戶j 之間的路徑上信息素濃度為τij（t）；初始時各路徑的信息素濃度相同，設為常數τij（0）=τ0；客戶坐標設為（x，y），其中客戶i到j的距離公式為：

（3）算法設計

職業教育人才的培養，有其特殊的一面，更強調實踐性和創造性。因此，在具體的質量評價中，亟需企業的參與，形成以職業能力評價為導向，企業等用人單位、院校教師、校外指導教師等多主體共同參與的質量評價體系。

當前螞蟻在客戶i，只考慮信息素濃度對螞蟻選擇路徑的影響：

①參數說明

allowedk：第k（k=1，2，...，m）只螞蟻暫未訪問的客戶集合，即接下來可以選擇的客戶；t 時刻第k 只螞蟻從客戶i 轉移到客戶j 的概率，值越大，前往客戶j的概率就越大；s：暫未訪問的客戶集合（allowedk）中的某一個客戶；對于j?allowedk，意味著客戶j 已經被訪問過了，則被選擇的概率為0；初始第k 只螞蟻隨機在某一客戶，則集合allowedk中有（n-1）個元素；接下來螞蟻根據（n-1）個非0 的的值，前往下一個客戶。此時有（n-2）個元素，繼續計算下一個目標客戶，直至集合為空，代表螞蟻遍歷了所有客戶。

②公式分析

由公式（14）可知，這是基于只考慮信息素濃度的情況，所以在最初幾次迭代的時候，每條路徑的信息素濃度都很低。在t=0 時，信息素濃度是透明的，每條路徑的信息素濃度都相等，導致螞蟻選擇路徑的隨機性非常大。為了解決這個問題，在公式（14）的基礎上引入新的變量，公式如下：

公式（15）相比較于公式（14），距離d 也是概率計算時需要考慮的因素。從客戶i 到客戶j 的路徑距離越小，1/dij的值越大。假如在信息素濃度τ 一樣的時候，若1/dij的值越大，則概率P 越大，螞蟻選擇較短路線的概率更大。

2.算法優化

從式(13)(14)(15)中可以看出，每只螞蟻在行走過程中都會釋放一定量的信息素，而信息素的濃度會隨著時間而變化，而螞蟻更大概率選擇信息素濃度更高的路徑。但蟻群算法有收斂速度慢、易陷入局部最優的缺陷，而α 和β 分別決定信息素濃度和轉移期望對螞蟻選擇可能性的貢獻程度。基于此，本文通過改進初始信息素分布及信息素更新方式優化算法設計。

（1）改進初始信息素分布

在初始條件下，各路徑上的信息素含量是相同的，此時蟻群處于盲目搜索階段，這時尋優效果差，搜索效率低。為此本文提出了一種改進的初始信息素分布方式，改進后的初始信息素分布為：

式(16)(17)中，C為常數，du,sg為轉移柵格到起點和終點連線的距離，即轉移柵格離起點和終點連線的距離越遠，該路線上的初始信息素濃度越低，反之就越高。因此，為避免初期螞蟻盲目搜索，通過設置分布不均勻的初始信息素以提高搜索效率。

（2）改進信息素更新方式

隨著迭代次數的增加，幾條較優路徑上的信息素差異越來越不明顯，導致蟻群收斂速度逐漸變得緩慢。本文結合精英蟻群算法，設計新的蟻群的信息素更新規則。在所有螞蟻個體完成一次迭代后，所有路徑上的信息素都會更新，為避免出現局部最優，加快后期最優路徑上信息素的積累，采取如式(18)的全局信息素更新方式：

三、實例分析

（一）算例描述

以福建省泉州市某生鮮電商宅配中心為例，從配送點(P0)向5 公里區域范圍內的10 個客戶點(P1,P2,P3,...,P10)配送多種生鮮產品，配送點（P0）的坐標為(110.408，21.201)，本文選取門店為起點建立平面直角坐標進行實驗。各客戶點詳細需求信息如表1所示，門店與客戶點、各客戶點之間的距離如表2所示。

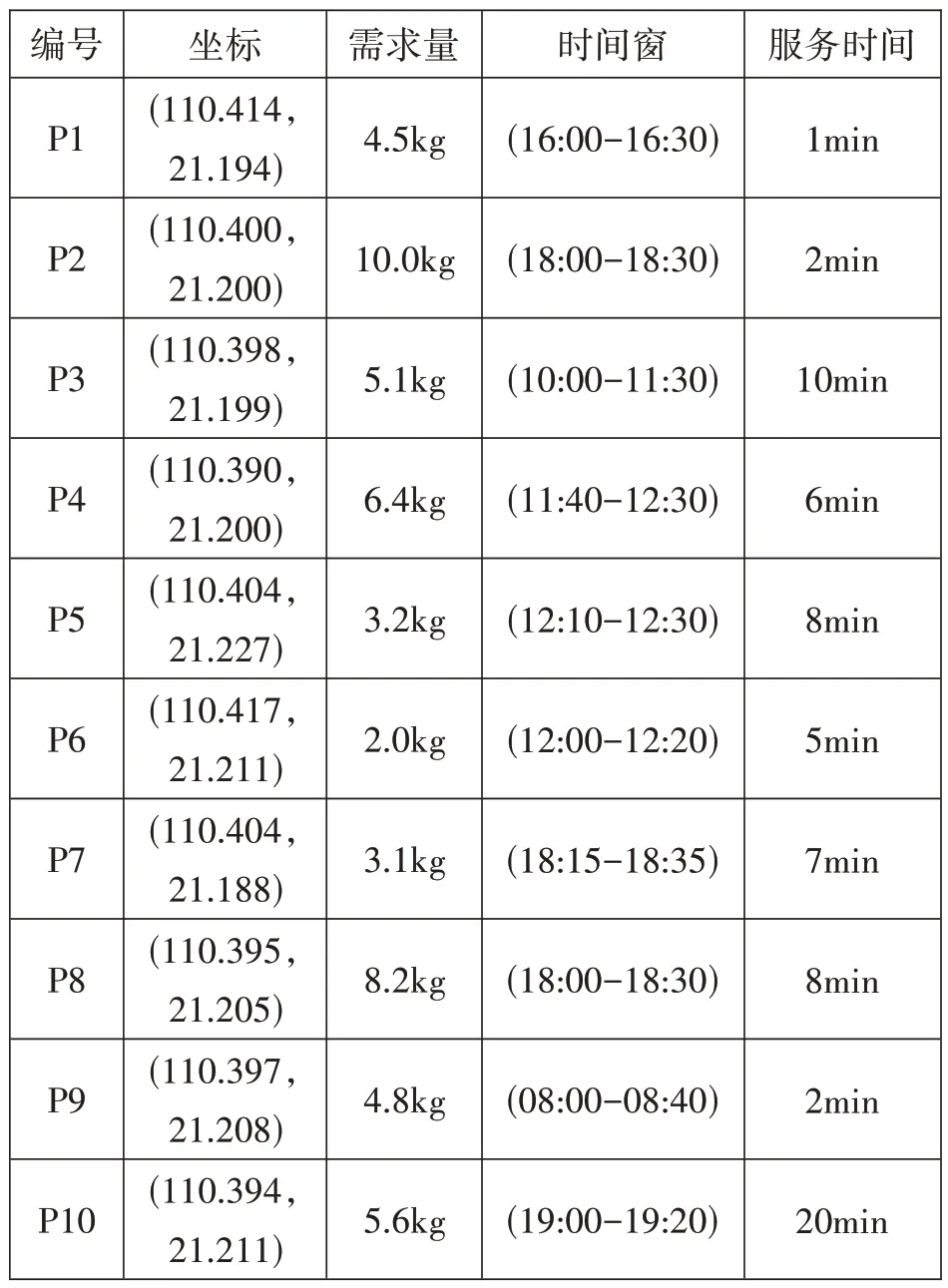
表1各客戶點詳細需求信息表

（二）實驗參數設置

本文的模型參數設定如下：

(1)配送車輛的最大載重量QM為25kg；（2）配送過程中勻速行駛速度為40km/h；（3）單位運輸成本為2 元/km；（4）車輛的固定成本F 為500 元/輛；（5）生鮮產品的平均單價P1為10 元/kg；（6）變質率a 為1%；（7）單位時間內的能耗E 為1.2元/h；（8）懲罰系數u 為20 元/h；(9)客戶需求量、客戶可接受的時間窗(表1)和門店與客戶、客戶與客戶之間的距離(表2)均已知。

蟻群算法初始參數設置如下：螞蟻數量為2，最大迭代次數Ncmax 為100，當Nc＜30 時，α=1，β=1，π=1，Q=100；當30＜Nc＜60 時，α=3，β=5，π=0.75，Q=50；當60＜Nc＜100 時α=5，β=1，π=0.5，Q=1。

（三）算法流程

為了使得改進算法更加穩定和快速地求解模型并得到最優解，本文綜合蟻群算法基本原理和改進方式，歸納出以下步驟：

步驟1：進行蟻群算法參數初始化。初始化的關鍵參數包括：信息素重要程度因子α、啟發函數重要程度因子β、信息素揮發因子π、信息素釋放總量Q，根據式(16)，設置當前迭代次數為Tij(0)=C+f(j)，最大迭代次數為Nc=100；

步驟2：初始化螞蟻群體。將m 只螞蟻隨機擱置在n個城市上；

步驟3：初始化螞蟻位置。構建禁忌表，并將Tabuk 清空，將螞蟻個體訪問的第一個城市放進禁忌表中，如禁忌表已滿，則轉至步驟4；

步驟4：狀態選擇轉移。在螞蟻未訪問過的城市，基于滿足客戶需求量和服務時間窗的約束進行各個因子值的選取，根據式(1)計算各條路徑的選擇概率Pij(t)，利用輪盤賭法選擇轉移點，并將下一步待訪問的城市置于Tabuk 表，直至螞蟻訪問完所有的城市；

步驟5：判斷是否所有螞蟻得到最優解，是則繼續進行下一步，否則回到步驟3；

步驟6：計算所有螞蟻的適度值，得到最優螞蟻個體及其相關目標數據，記錄最短路徑和總長度；

步驟7：當所有螞蟻完成一次循環后，路徑上的信息素需要根據式(18)進行更新，清空Tabuk 且轉至步驟4繼續迭代；

步驟8：當算法達提前設定的最大迭代次數，迭代結束，隨即得出最終的最小綜合成本及對應的最短配送路徑。

（四）結果分析

在操作系統為win11 的環境下，使用Matlab R2021b 編碼求解，Intel(R)Core(TM)i5-8250U CPU 1.6GHz(8GBRAM)進行求解，分別采用傳統蟻群算法和優化后的蟻群算法對生鮮電商冷鏈物流配送路徑優化模型進行求解10次，綜合成本的求解結果，如表3所示。

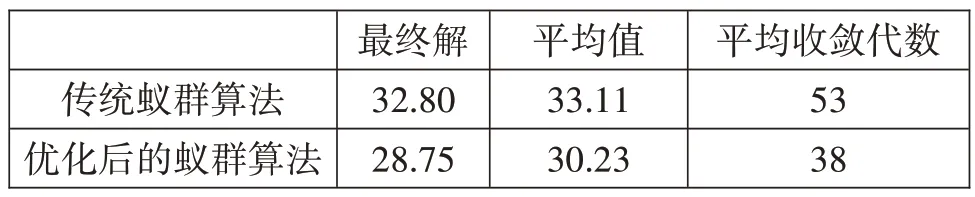
表3 蟻群算法優化前后求解結果

從表3中可以看出，優化前的蟻群算法求解得到的綜合成本最終解和平均值分別為32.80 和33.11，優化后的蟻群算法求解得到的綜合成本最終解和平均值分別為28.75和30.23。相比之下，優化后的蟻群算法求解結果分別比優化前的蟻群算法求解結果小4.05和2.88。這表明優化后的蟻群算法的求解優化效果和收斂效率均優于優化前的蟻群算法。

由圖1可得出優化前求解的配送路線，最短路徑長度為16.24 km。配送點的2 輛車為10 個客戶服務，車輛1 依次為客戶點P1、P7、P3、P2、P6提供配送服務，車輛2 依次為客戶點P9、P10、P8、P4、P5 提供配送服務，配送完成后車輛均返回配送點，可得出表4。

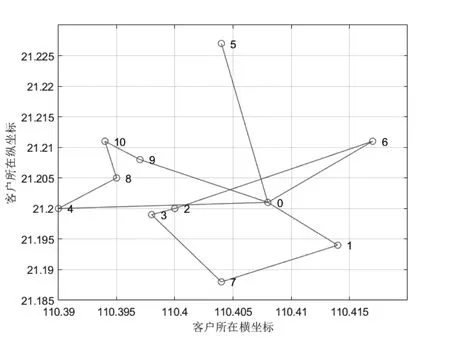
圖1 優化前的配送路線最短路徑圖

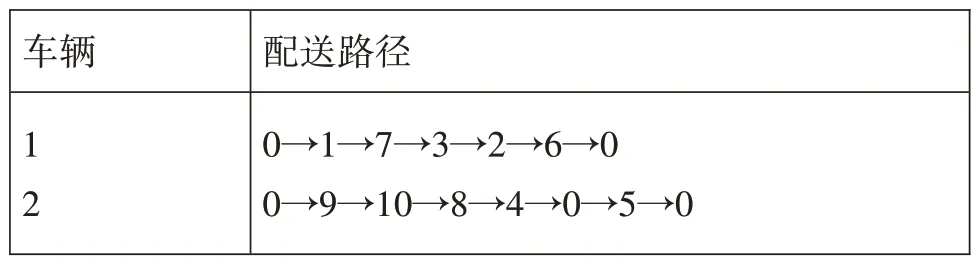
表4 蟻群算法優化前求解的配送路線

由圖2可得出優化后求解的配送路線，最短路徑長度為14.45km。配送中心的2 輛車為10 個客戶服務，車輛1 依次為客戶點P2、P3、P8 服務，車輛2 依次為客戶點P1、P7、P4、P10、P9、P6、P5服務，配送完成后車輛都返回配送點，可得出表5。

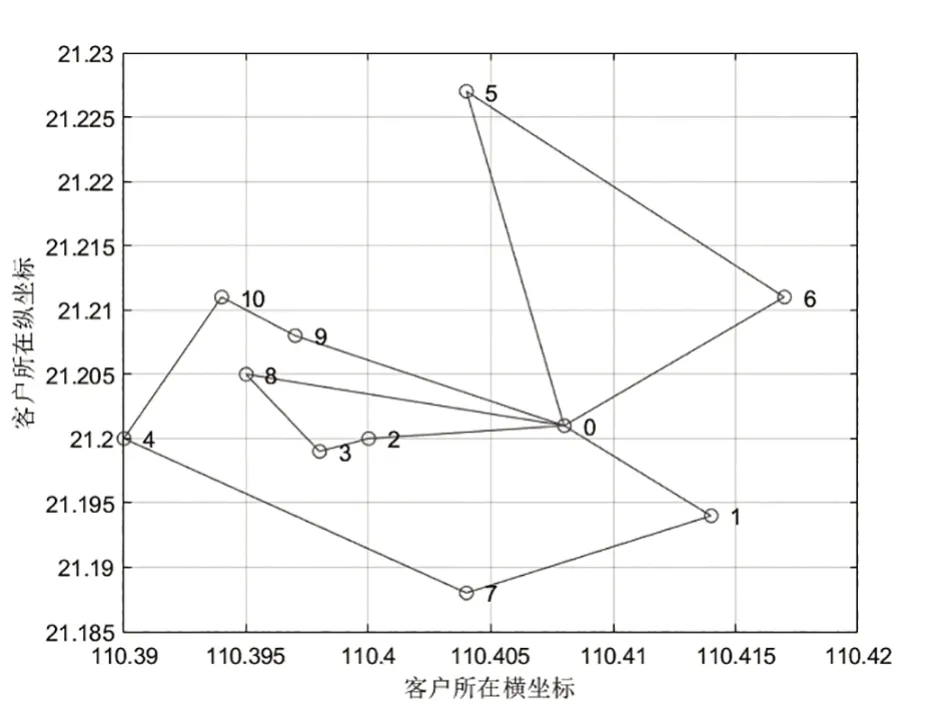
圖2 優化后的配送路線最短路徑圖

表5 蟻群算法優化后求解的配送路線

通過圖1 和圖2 的對比可以看出，優化前的配送路線減少了許多不必要的路徑交叉，最短路徑長度減少1.79km，提高約11%的速率，從而縮短配送時間的行駛里程，使得綜合成本更小化。結果表明，優化后的蟻群算法的初始信息素釋放速度和收斂效率均優于優化前的蟻群算法。

四、結論

針對低碳背景下冷鏈物流配送的熱點問題，通過綜合考慮生鮮冷鏈末端物流配送過程中的車輛固定成本、運輸成本、碳排成本等，以客戶需求量、車輛載重量和客戶要求服務時間窗為約束，構建以綜合總成本最小為目標的生鮮冷鏈物流車輛配送路徑優化模型。為了避免傳統蟻群算法的局限性，通過改進初始信息素分布和信息素更新方式，提出優化的蟻群算法并用來求解建立的車輛配送問題模型。實例仿真試驗結果表明，相對于傳統蟻群算法，優化后的蟻群算法求解車輛配送問題模型的效率更高，且能獲得效益更大的最優解，其主要體現于初期螞蟻搜索目的性增強，提高了搜索效率，后期收斂速度增快，有利于信息素積累，使得最短路徑總長度變小，從而降低綜合總成本。

綜上，本研究獲得生鮮電商冷鏈低碳配送路徑優化的成果，對冷鏈物流的低碳配送具有一定指導意義和應用價值，為生鮮電商冷鏈的低碳配送決策提供參考。