怎樣探索“乘法等式”與“比例”的轉化奧秘
藍海鵬

探索和理解“乘法等式”與“比例”轉化的奧秘,可采用如下教學過程。
一、根據比例的意義,多角度探索比例的結構
1.教師出示題目:①8∶4=10∶(? );②3∶9=4∶(? )③4∶6=2∶(? );④3∶8=9∶(? )。
2.小組交流。教師引導學生思考:你是怎么想的?有哪些方法?還發現什么規律?
3.全班交流。小組匯報得到4種方法。
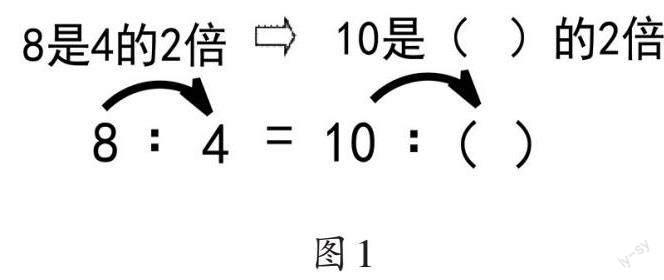
方法1:看前后項,根據比的前后項的倍數(或幾分之幾)關系求解。如題目①,等式左邊比的“前項是后項的2倍”,因此等式右邊比的前項也是后項的2倍,題目即轉化為10是(? )的2倍(如圖1)。
方法2:看“同類”項,根據等式兩邊比的前項(或后項)的倍數(或幾分之幾)關系求解。如題目③,等式左邊比的前項是等式右邊比的前項的2倍,則題目轉化為求6是(? )的2倍。
方法3:根據比例的基本性質,即比例中“內項之積=外項之積”求解。如題目④,比例內項之積=8×9=72,外項之積=3×(? ),根據比例的基本性質可將題目轉化為3×(? )=8×9,即(? )=8×9÷3。
方法4:改寫成分數形式,根據除法意義求解。如題目①可以改寫成[84=10(? )],利用除數=被除數÷商求解。
二、根據乘法等式,用多種方法寫比例
教師出示題目:已知24×3=8×9,請你寫出所有比例。學生先獨立完成,再全班交流。
方法1:固定內外項排序法。比例的基本性質為 “內項之積=外項之積”,也就是說,乘法等式的一邊分別是比例的其中一個內項或外項(如圖2)。
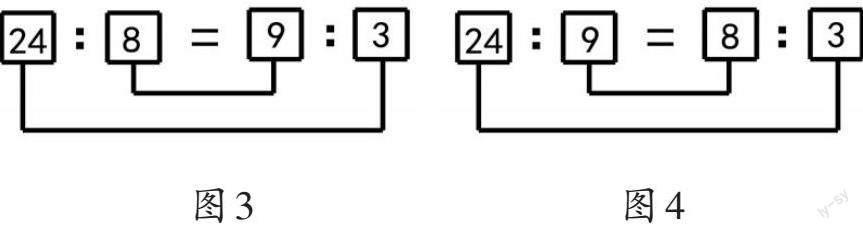
(1)把24和3作為外項,可以寫出4個不同比例(如圖3~圖6)。
(2)把8和9作為外項,同樣可以寫出4個不同比例。
師生共同小結:共有8種排列方法,即一個乘法等式可寫出8個不同的比例。
方法2:固定第1項排序法。將24×3=8×9中的3、8、9、24填到□∶□=□∶□中。即先選一個數填在比例的第1項,再填寫第2~4項。最終可得到8個不同的比例:第1項填3,可得3∶8=9∶24或3∶9=8∶24;第1項填24,可得24∶8=9∶3或24∶9=8∶3;第1項填8,可得8∶24=3∶9或8∶3=24∶9;第1項填9,可得9∶24=3∶8或9∶3=24∶8。
以上教學,揭示了“乘法等式與比例”互相轉化的奧秘,發展了學生的思維能力。
(廣東省清遠市教師發展中心)

