WiGNet:一種適用于無線感知場景的手勢識別模型

馬凱凱,段鵬松,孔金生

(鄭州大學網絡空間安全學院,450000,鄭州)

隨著物聯網及人工智能技術的快速發展,人機交互技術(HCI)的使用場景越來越多[1],手勢識別技術也成為學術界和工業界的研究熱點之一[2-3]。利用手勢識別技術,人與設備的交互更為便捷,其相關技術及應用在萬物互聯背景下潛力巨大。例如,在智能家居中,可以使用手勢控制電視、空調、冰箱等家用設備,而無需額外的控制器,能極大提升用戶的使用體驗和操作效率。

目前,實現手勢識別的主流技術可以分為基于計算機視覺[4-5]、專用傳感器[6]和射頻信號[7]三類。其中,基于計算機視覺的手勢識別技術通過收集大量的手勢照片,利用機器學習等技術學習和識別具體手勢信息。該技術研究成果較多,識別精度也較高,但存在弱光照條件受限及低隱私保護等缺點。基于專用傳感器的手勢識別技術通過專用傳感器(如可穿戴設備)采集手勢動作,再通過內部自帶的識別系統感知手勢類別[6]。該技術在手勢識別粒度及精度上有較大優勢,但安裝和維護成本較高,難以實現大規模應用[8]。基于射頻信號的手勢識別技術通過分析信號的變化情況實現手勢的分類,其中基于Wi-Fi信號的手勢識別技術因其易部署、成本低、非接觸式、隱私保護性好等優勢,逐漸受到研究者的青睞。

在早期的Wi-Fi手勢識別研究中,研究者通常使用接收信號強度指示(RSSI)作為感知特征載體。Abdelnasser等提出了一種通過分析RSSI變化來感知用戶手勢系統的WiGest[9],在單個無線設備接入點實驗條件下實現了87.5%的識別準確度。由于多徑效應,RSSI測量的是多路徑信號的疊加結果,無線感知的識別易受室內布局影響,因此RSSI僅能感知粗粒度的目標行為(如走動、跳躍等)。對于細粒度的目標行為(如手勢動作等),則需要通過信道狀態信息(CSI)來感知。CSI可以從一個數據包中同時測量多個子載波的頻率響應,而非全部子載波疊加的總體幅度響應,從而更加精細地刻畫頻率選擇性信道。隨著CSI Tool[10]工具的開源,使得從商用Wi-Fi設備中提取CSI成為可能,基于CSI的手勢識別研究也逐漸占據主導。2016年,Tan等提出了利用CSI進行細粒度手指動作的系統WiFinger[11],實現了93%以上的動作識別準確率。但是,由于WiFinger只選擇了關鍵子載波的感知數據,造成了大量的數據浪費和信息丟失。Han等提出的DANGR[12]使用生成對抗網絡對感知數據進行增強,降低數據集不完整引起的過擬合風險,最終達到了94.5% 的手勢識別平均準確率。Meng等提出的FaSee[13]通過使用動態時間規整算法,使手勢識別的平均準確率達到了94.75%。但是,該算法需要和k-最鄰近分類算法相結合,時間復雜度較高。

現有基于Wi-Fi感知技術的手勢識別研究中,大多數研究者從CSI中選擇特定子載波,并基于一維時序數據流進行特征識別[11,14],未能很好地利用不同頻率子載波之間的空間特征差異,使得感知特征辨識度較低,且噪聲信息不能有效濾除,導致難以實現高準確率的手勢識別。為解決此問題,本文在以下方面做出改進。

(1)提出了一種具有較高辨識度的感知特征表征機制。首先,將采集到的一維時序CSI數據重構為多維矩陣形式,以提取載波內和載波間所蘊含的手勢特征;其次,對重構后的多維感知數據進行二維離散小波變換(2D-DWT),以進行時間和空間層面上的數據降噪和平滑,得到具有較高辨識度的感知特征表征機制。

(2)本文提出了一種基于深度學習的高精度手勢識別模型WiGNet。WiGNet以2D-DWT處理后的多維矩陣為輸入,由多個NGConv模塊構成的卷積神經網絡組成。自建數據集和公共數據集上的實驗結果均表明,WiGNet相比同類模型有明顯優勢。

1 問題定義

1.1 信道狀態信息

信道狀態信息是在正交頻分復用(OFDM)技術中估計信道狀態的信息[15]。通常來說,每一條無線鏈路有多個子載波,每一個子載波都會產生對應的CSI值。

當信號在無線信道中傳播時,會遇到路徑中物體的反射、折射等擾動,這些擾動最終體現為接收端的CSI數據。假設接收端的和發射端的無線信號分別為α和β,則有

α=Hβ+a

(1)

式中:a為無線信號傳播過程產生的噪聲向量;H表示所有子載波組成的信道矩陣,如果把噪聲表示為a～cN(O,S)形式的正態分布,那么就可以估計出信道矩陣H

(2)

對于H的估計就是CSI的值,對于單個子載波來說,可以用以下形式表示CSI

h=|h|ejsinθ

(3)

式中|h|表示CSI的振幅。當人在無線信道中做手勢動作時,|h|就會產生相應的變化,通過分析這些變化就能實現對不同手勢的檢測。

1.2 問題定義

每一個OFDM信道中每一條子載波可以得到一個CSI序列。假設有一個具有Ns個發射器天線,Nr個接收器天線的系統,則每個接收到的CSI數據包都可以解析出Ns×Nr×n個CSI序列,其中n表示每個無線信道中子載波的數量。為了獲得CSI數據流,需要在接收端持續采集時間間隔為T的CSI數據,每個子載波可以得到一個長度為T的CSI序列。目前大部分基于CSI的手勢識別研究大都僅使用單個子載波的CSI數據進行分析實驗,其形式如式(4)所示

X=[h1,k,h2,k,…,ht,k,…,hT,k]T

(4)

式中ht,k表示t時刻第K個子載波的數值。每個子載波間手勢特征變化不總是相同的,為了更好地利用不同頻率子載波之間的空間特征差異,本文將每條無線信道間所有子載波的CSI序列重構為二維矩陣形式,如式(5)所示

(5)

根據Wi-Fi感知中OFDM和MIMO(multiple-input multiple-out-put)的技術特性,以及實際采集中多發射器、多接收器的場景,對于每個采集時間間隔T,可以得到Ns×Nr個如式(5)所示的二維矩陣。由于不同收發天線獲取的信號具有一定的差異,為了保留這些信號差異,本文將Ns×Nr個矩陣在深度方向堆疊,增強手勢動作的特征,消除不同無線信道間手勢特征的差異,提高魯棒性[16]。

2 模型設計

本文設計的手勢識別系統方案總體流程圖如圖1所示。

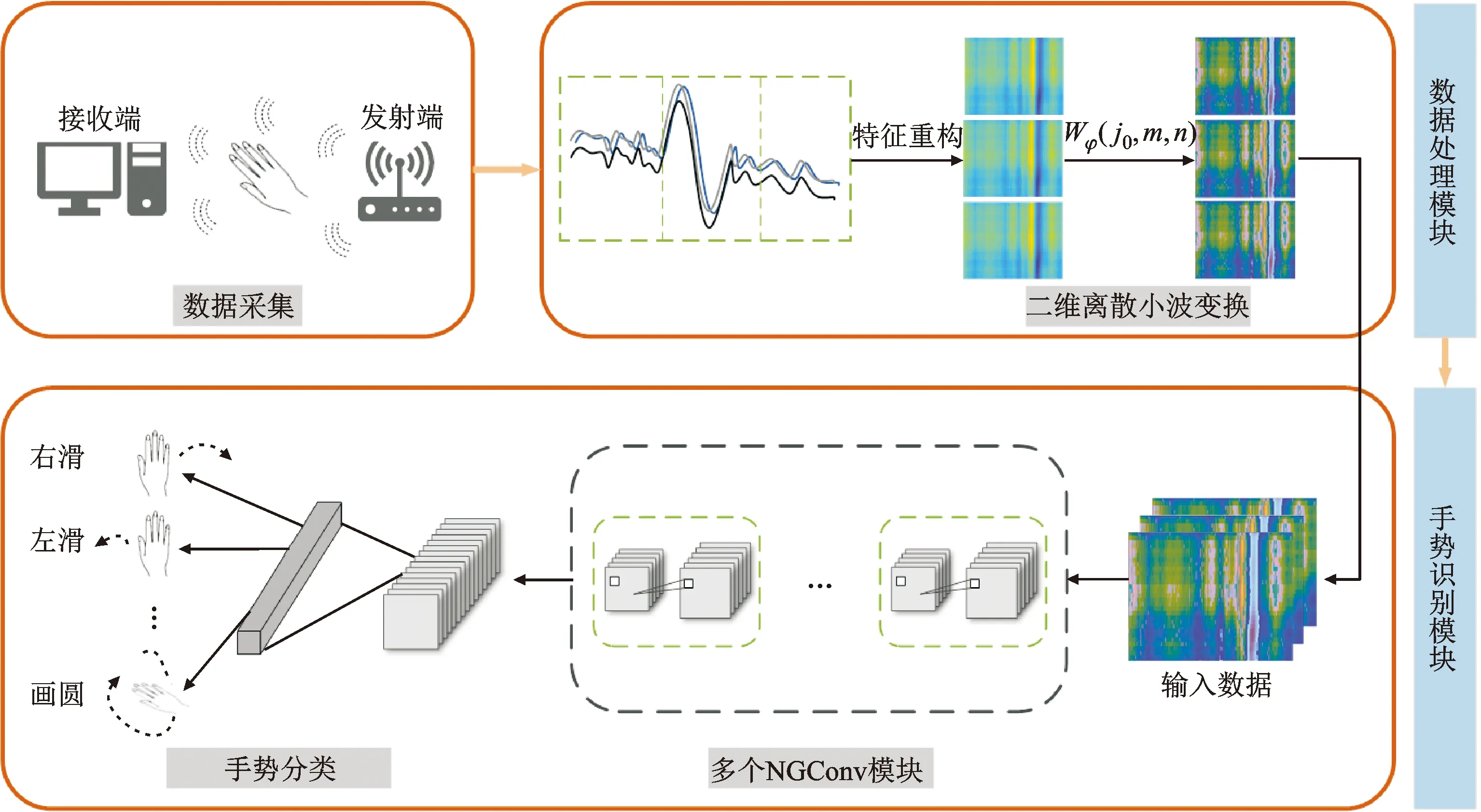
圖1 手勢識別總體流程圖

首先,使用收發設備獲取包含不同手勢特征的CSI數據;其次,將采集得到的CSI數據重構為tensor格式的二維矩陣形式,并對重構數據進行2D-DWT變換等達到降噪和平滑的目的;最后,將處理后的數據放入設計好的深度神經網絡WiGNet中,提取手勢特征信息,并對不同手勢特征進行分類,實現手勢識別功能。

2.1 二維離散小波變換

在采集CSI手勢數據的過程中,Wi-Fi無線信號會受到墻壁、桌椅以及身體其他部位微小動作的影響,這些多徑效應會讓CSI信號產生細微波動。時間精度和頻率精度是小波變換在高頻和低頻時具有的特性,這使其可以聚焦到無線信號變化的所有細節,對時頻信號分析有很高的契合度。基于這些特點,本文對重構的CSI數據采用2D-DWT方法進行降噪和降維處理。

在對無線信號的處理中,需要將連續的小波及其小波變換離散化。假設f(x)表示無線信號,則其可以在子空間中用小波函數ψ(x)和尺度函數φ(x)的展開形式來表示,如式(6)所示

(6)

式中:x表示單個子載波的值;j0是任意的開始尺度;cj0,k為近似系數;dj(k)為小波系數。將式(6)展開即可得到正向的離散小波變換(DWT),如式(7)和式(8)所示

(7)

(8)

有些背景噪聲在一維信號中體現的是隨機性,但可能在二維信號中就顯示出很強的區域性或較明顯的特征性。由于DWT只能在無線信號的時間維度上運作,為更好地利用不同頻率子載波之間的空間特征差異,本文引入了2D-DWT。對于重構數據,2D-DWT不僅能在無線信號的時間維度上運作,還能對不同子載波間的CSI信號進行平滑降噪處理。

在二維的情況下,給定尺度函數φ(x)和小波函數ψ(x),可以組合出1個二維尺度函數和3個二維小波函數,分別如式(9)～(12)所示

φ(x,y)=φ(x)φ(y)

(9)

ψT(x,y)=ψ(x)φ(y)

(10)

ψV(x,y)=φ(x)ψ(y)

(11)

ψD(x,y)=ψ(x)ψ(y)

(12)

式中T、V、D分別表示列方向、行方向、對角線方向。

于是,對于大小為M×N的二維矩陣f(x,y),其離散小波變換如式(13)和式(14)所示

(13)

i={T,V,D}

(14)

如同一維的情況,j0是一個任意開始的尺度,尺度j0處的近似由式(13)定義。圖2直觀地表示了2D-DWT如何對矩陣從水平和豎直兩個方向進行處理。其中a是原始矩陣,b是經過一階2D-DWT處理后的矩陣,c是經過2階2D-DWT處理后的矩陣,以此類推。

圖2 矩陣的2D-DWT處理過程

本文所使用的小波函數為多貝西(Daubechies, db)小波函數。在使用2D-DWT對數據處理時使用tensor數據格式,此格式已被證明能加快數據處理速度[17]。頻率能量圖[16]是CSI數據的可視化表示,圖3所示分別為經過2D-DWT處理前和處理后的2種手勢動作(上滑、畫圓)的頻率能量圖,其中橫軸表示采樣時間,豎軸表示子載波數量,顏色表示CSI數據的大小。可以直觀地看出,經過2D-DWT處理后,數據的尺寸變小,頻率能量圖信號的變化情況更加突出。3.2節的實驗也證明了經過2D-DWT處理后的數據提高了手勢識別的準確率,降低了系統整體運算時間。

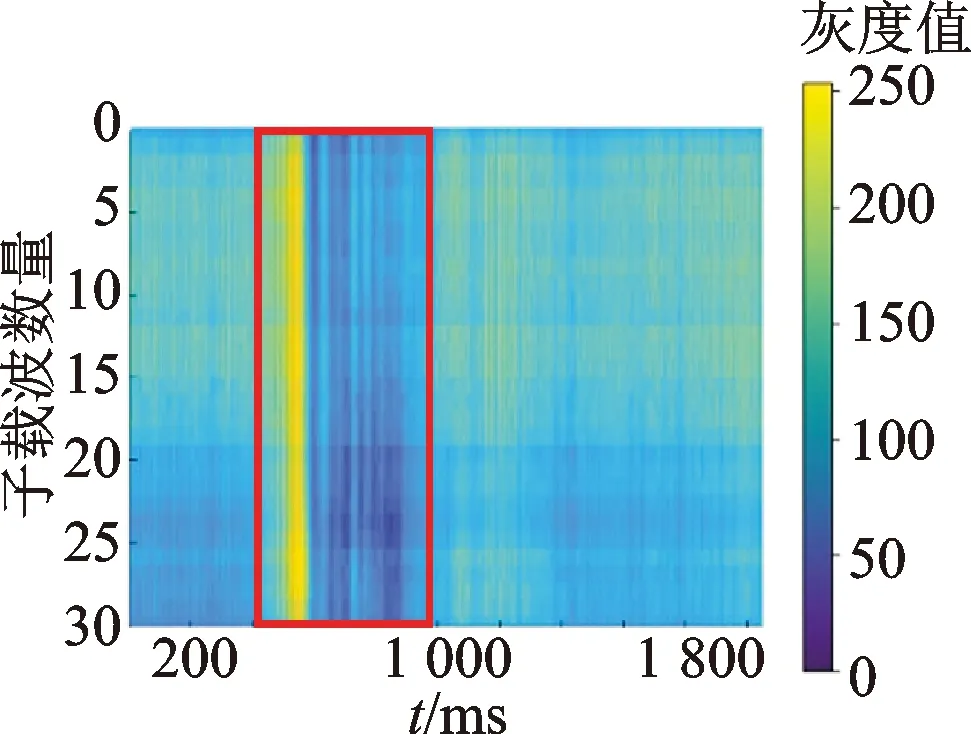
(a)上滑,處理前

2.2 WiGNet模型

對原始CSI數據重構后,考慮到卷積神經網絡在多維矩陣特征提取方面的巨大優勢,本文使用神經架構搜索技術(NAS)[18-19]搜索網絡深度以及卷積核個數的合理化配置,使用搜索得到的網絡提取數據特征,進行手勢分類。

2.2.1 神經架構搜索技術

NAS指一系列搜索神經網絡架構的算法,其思想為:首先定義一組可能用于網絡的“構建塊”(如卷積核、池化層等)。在NAS算法中,控制器遞歸神經網絡對這些構建塊進行采樣,將它們放在一起創建某種端到端架構。這種架構的風格通常與經典的網絡設計相似,如ResNet[20]或DenseNet[21],塊之間的組合和配置是它們之間的主要差別。然后,小規模訓練這種新的網絡體系結構,在獲得一定的精度后通過生成更好地體系結構更新控制器。

在搜索過程中,增加網絡的深度能夠得到更加豐富、復雜的特征,但網絡深度過深往往會產生過擬合、梯度消失等問題。增加網絡的寬度(卷積核的個數)能夠獲得更高細粒度的特征并且也更容易訓練,但對于寬度很大而深度較淺的網絡往往很難學習到更深層次的特征。結合重構后CSI數據的特點,本文使用NAS技術得到了更加適合重構后CSI數據的網絡結構。

2.2.2 注意力機制結構

本文加入了注意力機制結構以聚焦無線信號的關鍵信息。當手勢做出動作時,無線信號會發生特定的波動,注意力機制的引入能更好地提取波動變化信息。

如圖4所示,本文設計的注意力機制由一個全局平均池化層和兩個卷積層組成,第一個卷積層使用SiLU激活函數結構,第二個卷積層使用Sigmoid激活函數,其輸出和注意力機制結構的輸入在深度上堆疊以保留聚焦得到的特征。

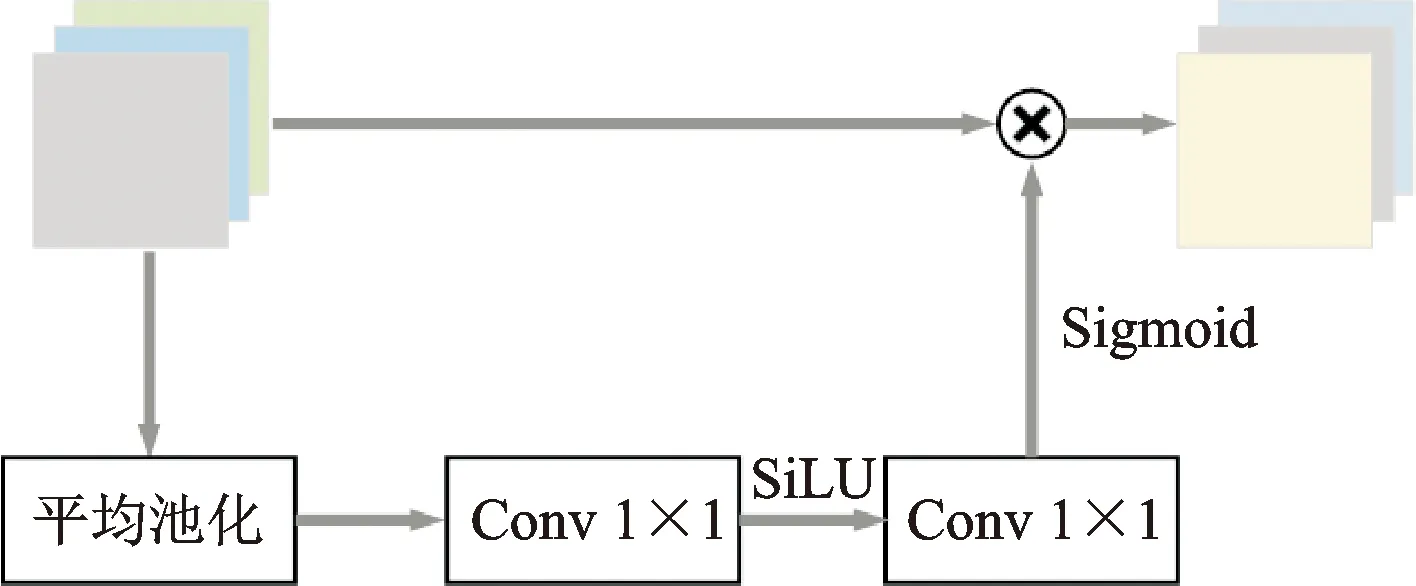
圖4 注意力機制結構

2.2.3 NGConv模塊

本文使用的網絡結構由8個NGConv模塊組合而成。如圖5所示,首先,數據經過一個卷積核大小為1×1的卷積層達到數據升維作用。之后,進行正則化和激活處理。正則化可以防止模型過擬合和加速模型收斂,激活函數選用SiLU激活函數,如式(15)所示,SiLU激活函數具有平滑、非單調、無上界有下界的特性。

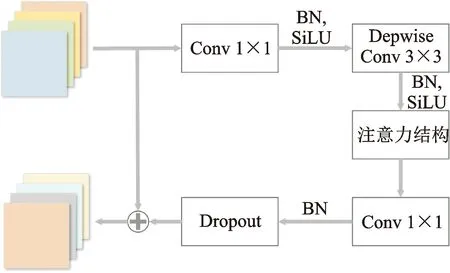
圖5 NGConv模塊示意圖

SilU(x)=x*Sigmoid(x)

(15)

然后,數據進入一個卷積核大小為3×3的深度可分離卷積層中[22],同樣經過正則化和SiLU激活函數處理后輸入注意力結構塊中。

最后,數據經過注意力機制塊處理后經過一個卷積核大小為1×1的卷積層以降低矩陣維度,經過正則化層之后使用Dropout操作防止模型過擬合,其中Drouout率設置為0.2。

NGConv模塊還使用了殘差連接操作[20],如式(16)所示

xl+1=h(xl)+F(xl,Wl)

(16)

在輸入下一個模塊之前,每次經過NGConv模塊處理的數據都會和輸入數據相加,殘差連接能很好地解決梯度消失和網絡退化的問題[20]。

數據在輸入WiGNet模型后,先進入一個卷積核大小為3×3的卷積層,之后由8個以線性結構連接的NGConv模塊進行特征提取,最后經由卷積核大小為1×1的卷積層展開為各個手勢動作的預測值。

3 實驗與分析

3.1 實驗設置

3.1.1 數據集描述

本文分別使用自建采集的數據集和公共數據集評估模型的性能。

由于無線信號的傳播會受到多徑效應的顯著影響,因此不同多徑效應下無線信號的效果有一定區別。考慮模型在不同多徑效應環境下的運行效果,弱多徑效應環境遮擋物少,環境開闊,信號傳播路徑相對簡單;強多徑效應環境物品較多,信號傳播路徑較為復雜。為保證實驗數據的多樣性和客觀性,在采集數據時選擇了弱多徑效應的數據采集室和強多徑效應的學生實驗室兩種環境,如圖6所示。

(a)數據采集室

發射器選擇具有一個發射天線的TP_LINK AC1750無線路由器,接收器為一臺具有 3個接收天線安裝有開源CSI Tool工具的計算機。采樣頻率為1 kHz,Wi-Fi工作頻率為5 GHz。如圖6所示,發射器和接收器相距2 m,考慮到視距路徑和非視距路徑對無線信號傳播的影響,消除位置誤差并結合現實情況,在發射器和接收器中間選擇3個不同位置進行CSI數據的采集,采集過程中受測者始終面向接收器。每次接收含90(1×3×30)個子載波的CSI數據。本文在每種環境下分別安排2個受測者,兩種環境下每個受測者分別采集9種手勢動作,分別為左滑、右滑、上滑、下滑、畫O、畫十、畫Z、畫W、畫S,每次采集時間間隔為2 s,每種動作在每個采集位置處采集20條數據,處理后得到2 160條數據。

公共數據集[23]在教室、大廳、辦公室3個實驗地點采集。使用的接收設備是配有Intel 5300無線網卡的筆記本計算機。每個采集環境的設備和實驗布置相同,有一個發射器(每個發射器1條發射天線)、6個接收器(每個接收器3條接收天線),每個接收器每次接收含90(1×3×30)個子載波的CSI數據。本文選取數據集中的6種手勢進行實驗,分別為拍手、橫掃、畫O、推拉、擺動、畫Z。每個實驗地點分別選取4個受測者的手勢數據。對于每個實驗地點,每種手勢動作各整理了1 500個數據,每個地點分別整理9 000個數據進行實驗。

自建數據集和公共數據集主要參數設置如表1所示。

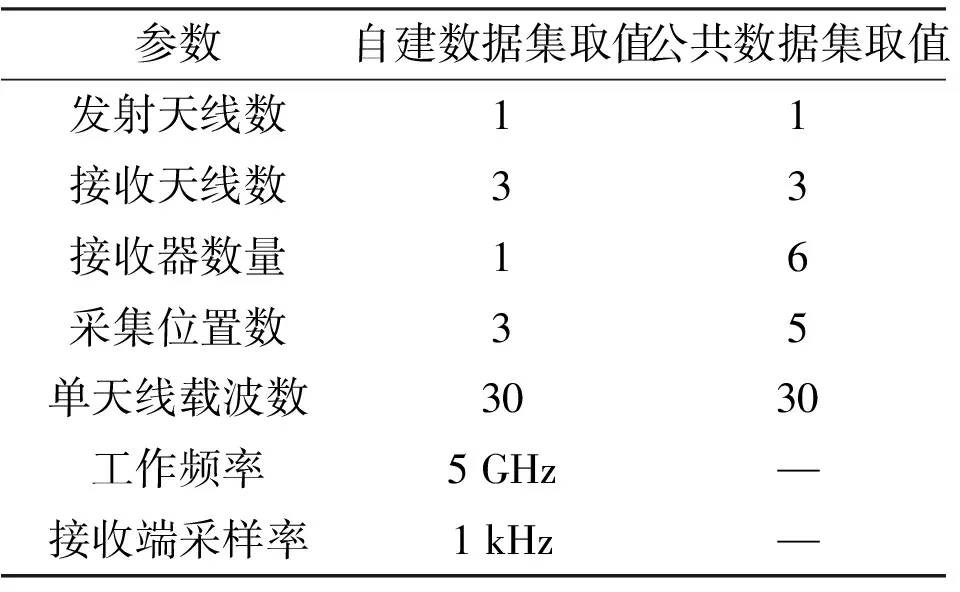
表1 數據集主要參數設置

3.1.2 模型超參數

本文實驗基于深度學習框架PyTorch實現。優化器使用隨機梯度下降算法(SGD),其動量因子設置為0.9,L2正則化參數設置為0.000 5以防止過擬合。Batch_size設置為16。初始學習率設置為0.01,并使用余弦學習率衰減策略優化學習速度[24],最終學習率下降為0.000 1。將每個環境的數據劃分為80%訓練集和20%測試集,使用測試集評估識別效果。

3.1.3 評估指標

本文采用準確率(A)、精確率(P)、召回率(R)、特異度(SP)、方差評估模型效果。模型最終需要判斷樣本的結果是正確(positive)還是錯誤(negative)。以FN表示真實值是positive,預測值是negative的數量;TP表示真實值是positive,預測值是positive的數量;TN表示真實值是negative,預測值是negative的數量;FN表示真實值是negative,預測值是positive的數量;S2為總體方差,Y表示預測值,N為數據總數。準確率指正確分類樣本數占總體樣本數比例;精確率指預測的所有positive中,預測正確的比例;召回率指預測正確的positive占所有真實positive的比例;特異度指預測正確的negative占所有真實negative的比例。方差描述的是訓練模型中每個預測值與預測均值差的平方和的平均數。評估指標的公式如下

(17)

(18)

(19)

(20)

(21)

3.2 實驗結果

為了評估所提出方法的性能:首先,本文驗證了所提出的2D-DWT方法的有效性;然后,給出了模型的最終分類結果并和現有模型的性能進行對比;最后,給出所提方法在公共數據集上的表現。

3.2.1 2D-DWT的有效性實驗

圖7為使用2D-DWT和不使用2D-DWT的準確率,分別在自建數據集中數據采集室和學生實驗室進行實驗。結果顯示:在數據采集室環境下,不使用2D-DWT的分類準確率為97.3%,使用2D-DWT的分類準確率為98.2%;在學生實驗室環境下,不使用2D-DWT的分類準確率為97.2%,使用2D-DWT的分類準確率為98.1%。

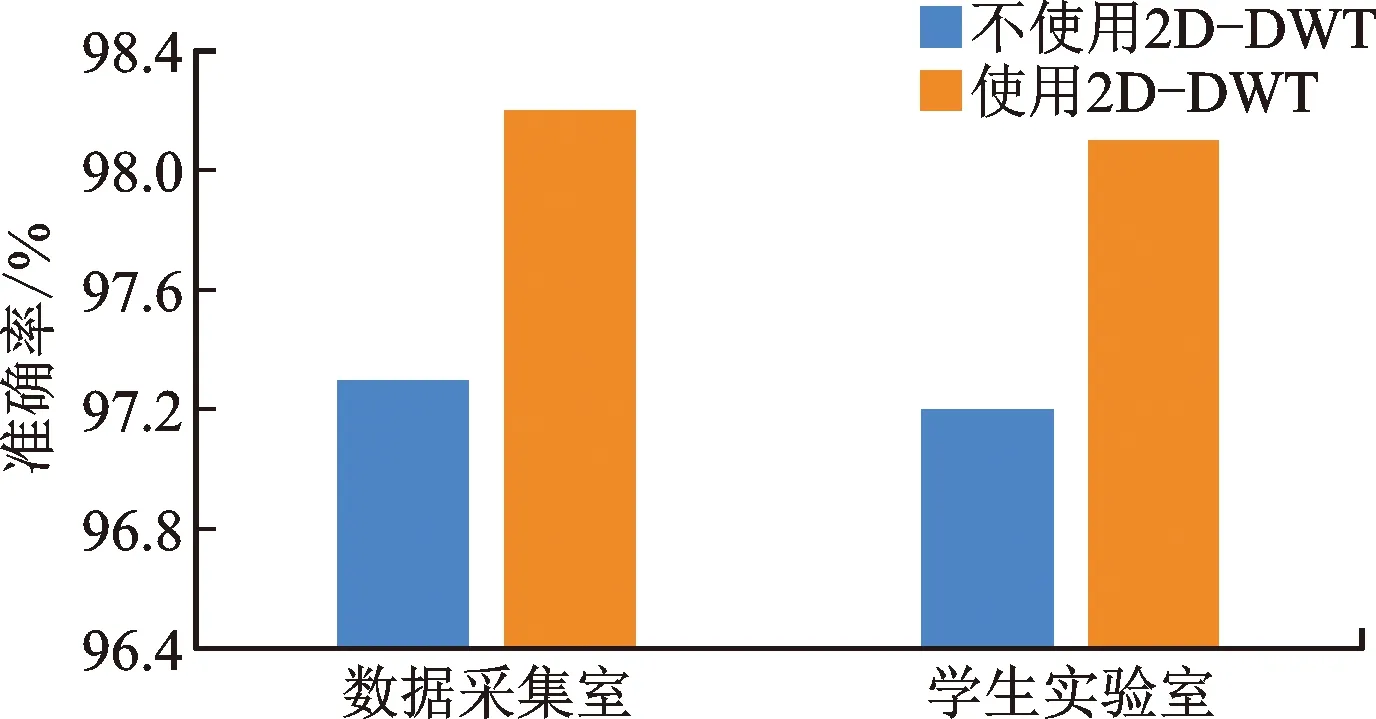
圖7 是否使用2D-DWT的準確率對比

圖8為不使用和使用2D-DWT情況下在數據采集室下訓練集損失隨時間變化圖。盡管對數據進行2D-DWT時會消耗一定的運行時間,但先進的處理方式[17]與處理后更小的數據尺寸使整體的運行時間更短。從圖中可以看出,使用2D-DWT訓練時損失值能夠更快地收斂。實驗結果充分說明,使用2D-DWT對數據進行降噪后,不僅提高了分類結果的準確率,還降低了訓練所需時間,證明了2D-DWT的有效性。

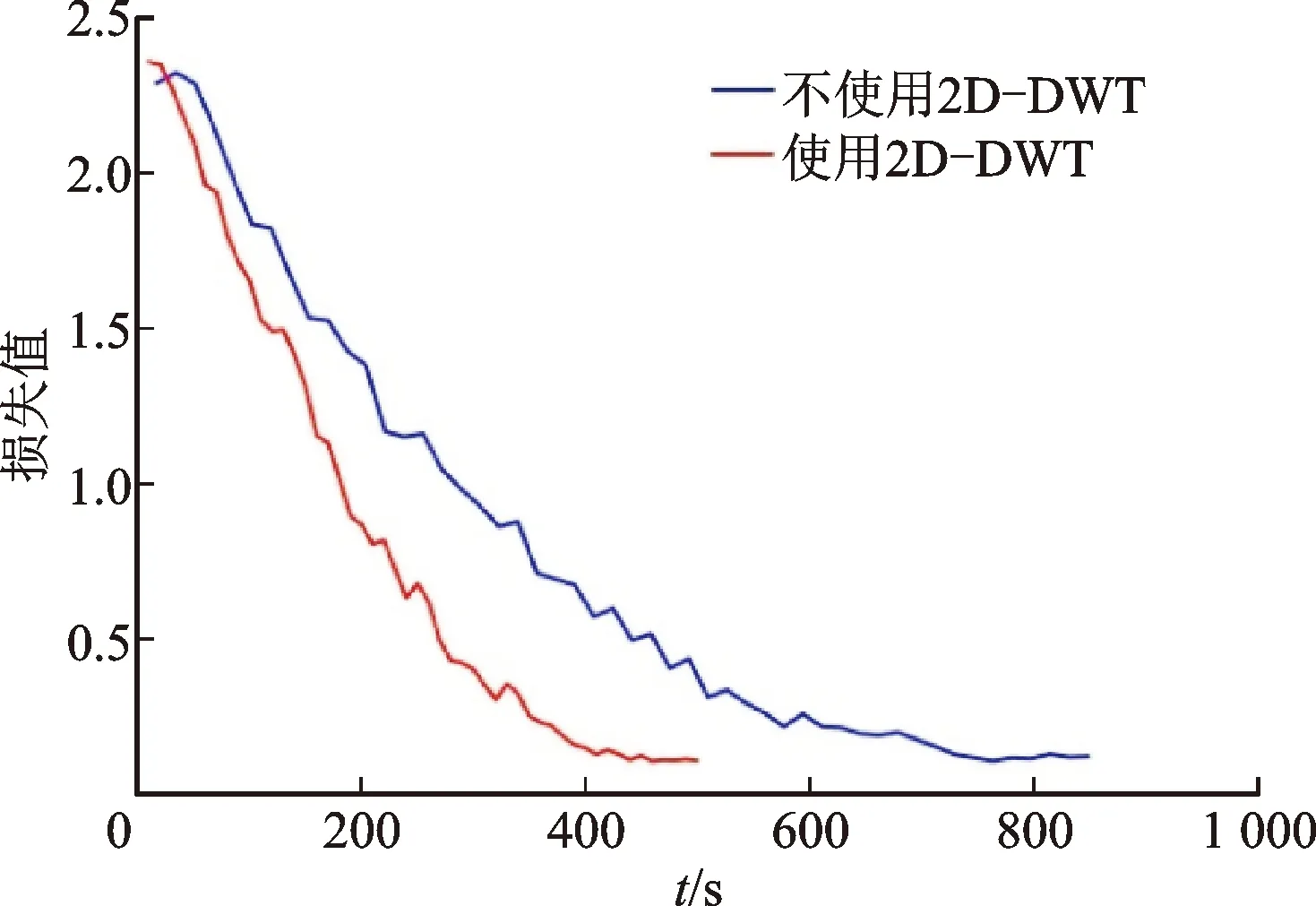
圖8 是否使用2D-DWT的loss變化曲線

3.2.2 系統整體性能

混淆矩陣可以觀察模型在各個類別上的表現。圖9為使用本文提出的基于WiGNet的方法對9種手勢動作的最終分類結果的混淆矩陣,其中橫軸表示實際的手勢動作,豎軸表示預測的手勢動作,對角矩陣表示每一種手勢動作的識別準確率。可以看出對于所采集的9種手勢動作,WiGNet對于每一種動作都有很好的分類效果,對于左滑、畫圓、畫S等區分度高的動作的分類最準確。兩種環境下識別準確率分別達到了98.2%和98.1%,表明WiGNet能實現高精度手勢識別,且具有一定的魯棒性。

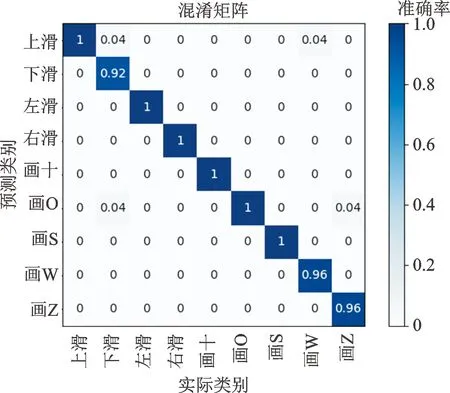
(a)標準數據采集實驗室

為了評估WiGNet的性能,將WiGNet和當前流行的手勢識別方法對比。本文使用在標準數據采集實驗室下的數據分別與經典分類模型ResNet50[20]、經過神經架構搜索技術改良的適用于本文數據集的最佳深度ResNet網絡ResNet36、手勢識別最新模型FaSee[13]進行對比,結果如表2所示。

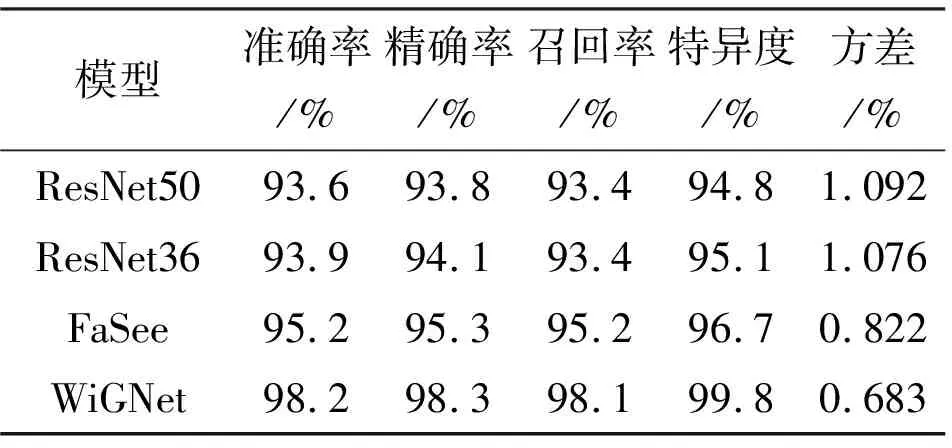
表2 不同手勢識別方法的結果對比

在訓練過程中發現,當ResNet50達到了一定的效果后,隨著輪次的不斷增加,訓練集和測試集的準確率相差變大,出現過擬合,具體表現為結果的方差較大;盡管ResNet36使用神經架構搜索技術得到了適合于本文數據集的網絡深度,但其表現和ResNet50相差不大,仍出現過擬合問題;本文提出的WiGNet采用更加輕量級的網絡,網絡深度更淺,并且在每個NGConv模塊中加入了dropout層用以防止過擬合,結果顯示WiGNet訓練結果的方差最小,模型穩定性更高,訓練效果更好;FaSee方法的效果雖然好于ResNet,但動態時間規整算法和k-最鄰近分類算法的時間復雜度高,開銷大,且其并沒有考慮各個子載波之間的空間特征,最終效果差于本文提出的WiGNet。從表2可以看出,不管是在識別準確率還是其他評估指標下,WiGNet相較于其他方法的效果都更好。

3.2.3 公共數據集結果

為了突出本文方法的高性能,本節將和使用相同公共數據集的方法對比,分別是Widar3.0[23]、CGRU-ELM[25],對比結果如表3所示,可以看出,WiGNet相較于其他方法具有更好的分類性能。

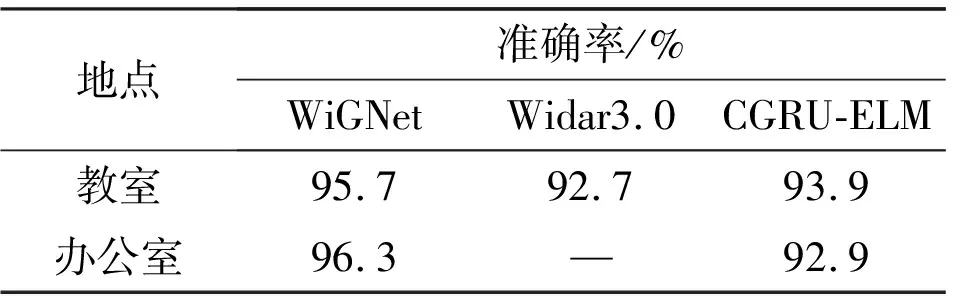
表3 公共數據集準確率對比

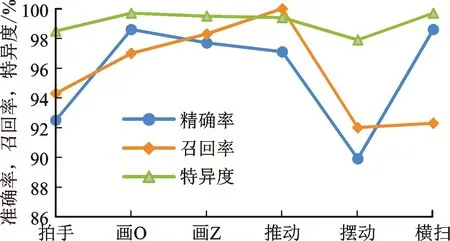
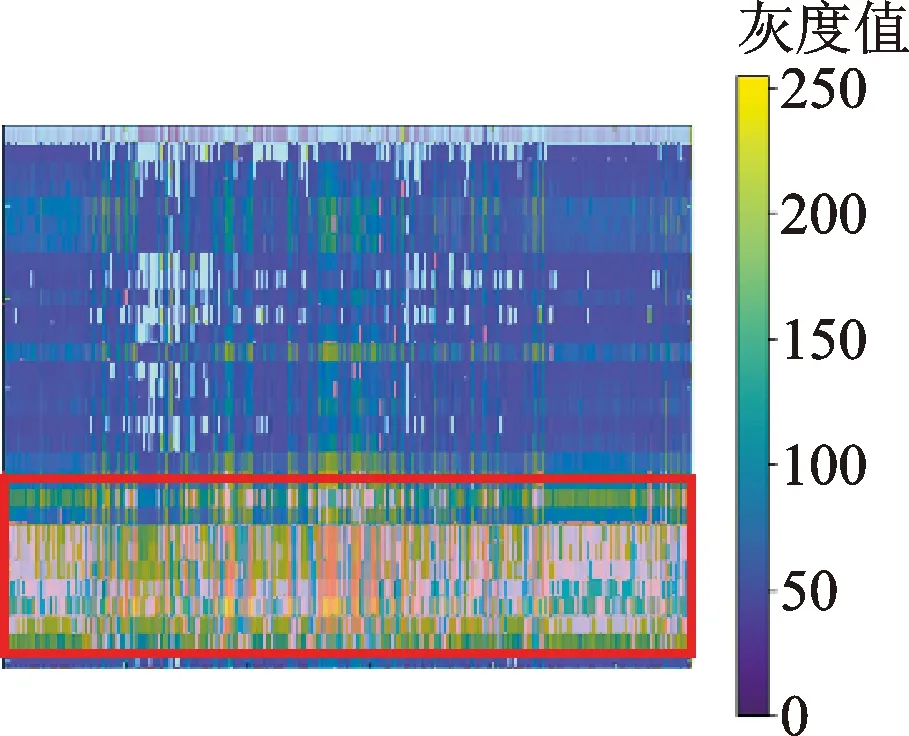
圖10展示了使用WiGNet在公共數據集上的評估結果。通過對兩個環境下的每個動作進行評估可以看出,對于畫Z、畫O等區分度高的動作的分類最準確,對于擺動、橫掃等動作的識別準確率相對較低。圖11所示為經過2D-DWT處理過后的擺動和橫掃動作的頻率能量圖,可以看出兩種動作的特征重合度較高,模型對于不同特征的提取相對困難。總體來說,對于兩個環境下的6種手勢動作,WiGNet對于每一種手勢動作都實現了較好的分類效果,兩種環境下的高準確率分類效果表明WiGNet具有較好的魯棒性。

(a)教室環境下評估結果

(a)拍手

4 結 論

傳統基于Wi-Fi的手勢動作識別模型,大多數研究者采用從CSI信息中選擇特定子載波,并基于一維時序數據流進行特征識別,這造成大量的數據浪費,未能很好利用不同頻率子載波之間的空間特征差異,存在因感知特征辨識度較低及難以提取而導致識別準確率不高的問題。本文首次將二維離散小波變換引入感知特征的重構流程中,實現了在時間和空間層面上的數據降噪和平滑。在此基礎上,本文還提出了基于深度學習的高精度手勢識別模型WiGNet。WiGNet以2D-DWT處理后的多維矩陣為輸入,能準確地提取手勢動作的特征。實驗結果表明,使用二維離散小波變換對數據處理能提高識別準確率和運算速度,提出的WiGNet在自建數據集和公共數據集上均有良好的識別分類性能,并且相比同類模型表現更好。

CSI含有豐富的無線信號信息,如振幅、相位、多普勒頻移、功率分布信息以及人體坐標系下的速度譜等,如何將這些信息結合起來,提高整體識別性能與適應能力可以作為未來的研究方向。