追求自然的數學教學
——蘇科版數學教材八（下）第五章“平面直角坐標系”教學過程分析

■陳磊

本節課是蘇科版數學教材八年級下冊第五章第二節的第一課時。平面直角坐標系是初中教材中的基礎性知識，是串聯“數”與“形”的重要載體，旨在構建點與有序實數對的對應關系，實現一維向二維的轉變。本課主要從學生的生活、數學學習經驗出發，建立新舊知識的聯系，關注學生概念自然生成的過程，培養學生的數學思維。

一、問題引導，激活舊知

問題1：有關七年級所學的數軸，同學們還記得哪些內容？

新課伊始，教師設計開放性的問題，讓學生各抒己見，在調動學生積極性的同時，指引學生深度回顧，為后續知識的自然生長打下基礎。

問題2：（教師給出一個數軸，如圖1）請同學們思考：（1）數-2、0、3 在數軸上是如何表示的？（2）數軸上的點P又如何表示？

圖1

學生舊知被激活后，教師從問題出發，讓學生回顧實數與數軸上的點一一對應，激活實數與點之間的聯系，讓學生重溫數形結合的思想。

二、情境引入，生活感知

問題3：2023 年春節檔國產電影好評如潮，同學們都看了嗎？小麗也買了一張電影票，她如何在電影院快速地找到座位？

對國產電影的肯定，能激發學生的自豪感和愛國情懷，起到學科育人目的；從學生實際生活出發，設置問題情境，讓學生初步感悟描述位置的關鍵點，為后面數學問題的研究創造條件。

三、經歷過程，生成概念

問題4：數學中，如何確定一個點在平面內的位置？（教師在黑板右上角放一個小磁力貼，記為點A）請同學們描述黑板平面內點A的大致位置。

大多數學生很快能根據生活經驗，不經思索“蹦”出答案：“右上角。”這說明對于八年級學生而言，他們通過生活經驗的積累，腦子里已經有了“隱形的平面直角坐標系”。“右”的描述，其實說明在其腦海里已經有了豎直的一條線；“上”的描述，其實說明在其腦海里也已經有了水平的一條線。這樣通過對學生生活經驗的喚醒，引出接下來要研究的數學內容，自然生成，而不是教師強拉硬拽。

在學生回答后，教師在黑板上畫出兩條相互垂直的直線。

問題5：剛才回答“右上角”很對，請小組交流如何更準確地描述該點在黑板平面的位置。

學生上黑板度量，量出該點到兩直線的距離，得出用兩個實數來表示的初步結論。

問題6：能將這兩個數據換個位置嗎？作點A關于豎直的直線的對稱點，那該對稱點又該如何描述呢？

通過問題串鋪設，讓學生結合生活經驗，先感悟有序，然后，面對“點A與所對應的有序實數對一樣”這個實際困難，學生自然想到用正、負來區別，順理成章地將已學數軸遷移到新知識的建構中來，自然地將兩條垂直的直線“生長”為兩條具有公共原點的相互垂直的數軸，生成平面直角坐標系、x軸、y軸、坐標原點等概念。

四、回顧歷史，感受文化

弗賴登塔爾曾強調對歷史的運用要體現“再創造”的過程，平面直角坐標系的發展最初起源于圓錐曲線研究的桎梏。對于八年級學生來說，這樣的歷史背景雖不能完全理解，但在教師解讀后，學生也能感受在歷史長河中平面直角坐標系產生的“自然”。另外，為激起學生的學習興趣，增加學習的趣味性，教師滲透笛卡爾觀察蜘蛛網從而發明了坐標系的故事，鼓勵學生在生活中多觀察，多思考，多感悟。

五、問題探究，深入理解

問題7：如何在平面直角坐標系中表示點A、B、C的位置？

如圖2，學生動手操作，由A點向x軸、y軸作垂線，垂足M在x軸上的坐標是3，垂足N在y軸上的坐標是4，我們說點A的橫坐標是3，縱坐標是4，有序數對（3，4）就叫作點A的坐標，記作A（3，4）。以此類推，點B的坐標為（-2，1），點C的坐標為（-3，-3）。

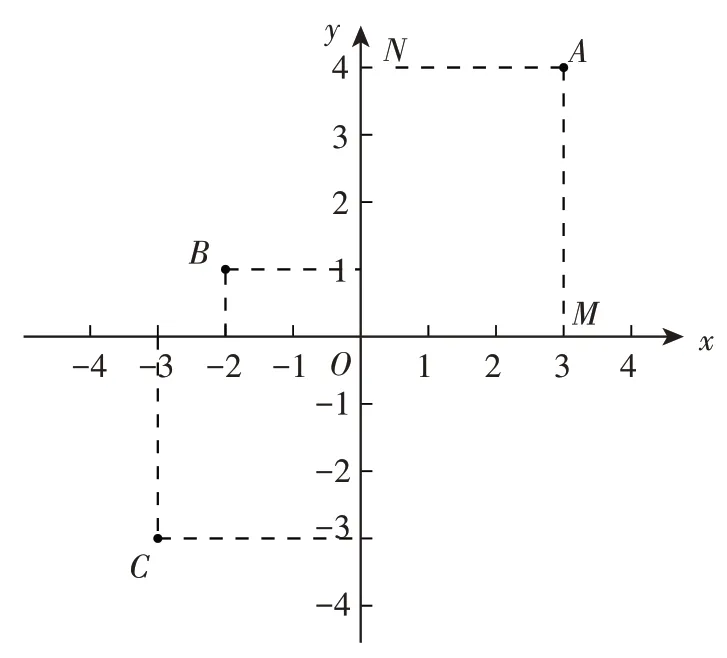
圖2

問題8：怎樣在平面直角坐標系中描出點（2，3）、點（-1，3）、點（2，-2）？

學生畫出圖形，歸納作圖方法：先在x軸上找到表示2 的點，再在y軸上找到表示3的點，過這兩個點分別作x軸、y軸的垂線，兩條垂線的交點就是點（2，3）。

問題9：數軸上的點與實數一一對應。通過剛才的研究，平面直角坐標系中的點跟什么存在對應關系呢？

教師引導學生從問題7 感悟平面內任意一點對應唯一一個有序實數對，反過來，通過問題8 感悟任意一個有序數對也對應唯一的一點。學生在動手動腦的同時自然感悟坐標平面內的點與有序實數對一一對應的關系。

問題10：觀察平面內不同位置的點，說出它們的坐標，并歸納出這些點的坐標分別具有什么特征。

學生在探究中，通過觀察、操作、歸納，最后得出結論，既是對數學概念的深入理解和掌握，也培養了分類的意識。

六、反思歸納，遷移延伸

問題11：請同學們帶著問題，回顧和總結本節課所學：

（1）什么是平面直角坐標系？

（2）數軸與平面直角坐標系的異同點有哪些？

（3）平面直角坐標系內的點與坐標之間有什么關系？

（4）平面直角坐標系將平面分成了幾個部分？每個部分的點的坐標有什么特點？

通過幾個問題，讓學生對本節課的知識進行梳理、歸納，并與之前所學的數軸知識建立聯系，通過對比，形成理性認識，將新知轉化為自己的認知。

問題12：大家觀察我們的教室空間，在我們這個教室空間里，對于講臺上的這個小粉筆頭（看成一個點），又該如何描述它的位置呢？

本節課學生通過探究，由一維走向了二維，自然會思考：三維位置又該如何表述？作為本節課的延伸，筆者讓學生課后查閱資料，自主探究，豐富學生的課后學習，也讓學生對未來的學習充滿期待。

夸美紐斯曾強調，我們的教學應遵循自然規律。數學概念的教學，是數學的邏輯起點，其產生與發展存在著自然性。我們的課堂在情境設置、問題串的設計等方面要立足學生的“最近發展區”，圍繞知識和能力的本質，以提升學生學科素養為目的，合情合理，追求自然。