談為什么要反對套路訓練
——以一道幾何最值題為例
劉春書
(江蘇省南京市板橋中學 210039)
學數學離不開解題,但許多人將其片面理解為學數學就是要大量刷題,導致數學教學中應試式的題型教學盛行,套路訓練泛濫,學生作業負擔沉重,創新意識和能力嚴重削弱.為糾正上述不良傾向、深化新時代教育評價改革,當前數學學科中高考命題出現了反題型、反套路趨勢,追求通法和大道.特別是當前立德樹人教育背景下,數學教學要關注學生數學核心素養的養成,解題教學更要反對套路化.下面以一道幾何最值問題為例來闡述當前解題教學如何尋求大道和通法,培養學生數學核心素養,兼談為什么要反對套路化的解題訓練.
例題如圖1,在四邊形ABCD中,AB=2,BC=BD,∠ADC=150°,∠DCB=60°,則AC的最大值是.
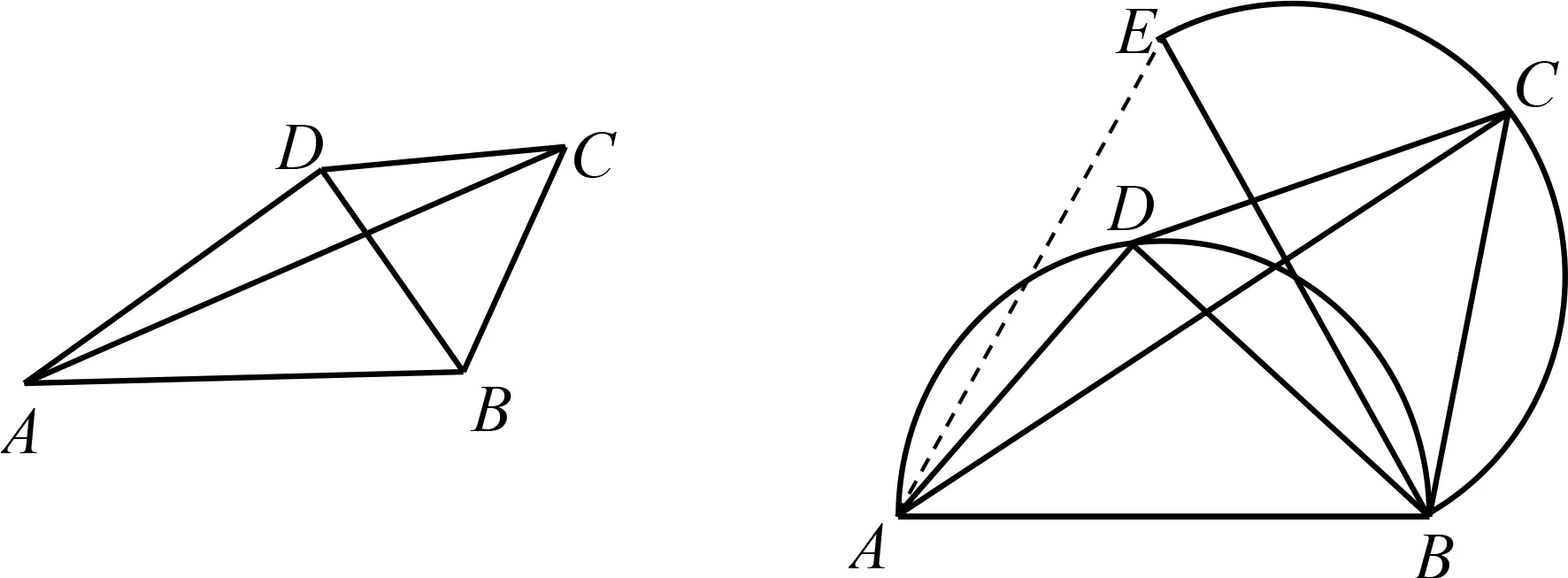
圖1 圖2
1 套路化的解題思路

2 套路化解題的反思
應用套路解決本題,只需根據“兩動點(點D,C)到定點(點B)的距離之比是定值(定值為1),夾角是定角(定角為60°)”特征,迅速觸發、啟用瓜豆原理“主動點在圓上——角+圓”的套路解決問題,實質上就是解題中的“條件反射”.至于怎么想到點C的運動路徑是半圓、為什么是半圓等本原性問題,即解題思路如何想到的問題,根本無需考慮.正因為缺少對本原性問題的探索、思考,“題目稍有變化,學生就會無從下手”的現象常常發生,而我們教師卻還在責怪學生靈活性不夠.
3 指向本原性問題解決的解題思路
解每一道題,肯定都是從這一道題的條件和結論出發進行思考.基于本題條件和結論的特點,指向本原性問題解決的思考有以下三個方向.
3.1 本原性思考方向一:基于運動路徑
基于運動路徑的本原性思考按以下三步走.
步驟一是分析條件定主從,明晰結論找關鍵.解題都需先分析條件、明晰問題.通過前面的分析,本題已知A,B為定點,D,C為動點,且點D的運動路徑是以AB為直徑的半圓,點C隨著點D的運動而運動.現在欲求AC的最大值,關鍵是找出點C的運動路徑.
步驟二是先猜想后驗證,確定運動路徑.動態圖形運動路徑的問題,我們可以先嘗試畫出動點的一些位置,一般包括起始位置、終止位置和運動過程中的幾個一般位置,然后再由這些位置猜測動點的運動路徑.圖3畫出了點C的三個位置,當點D在半圓上與點A重合時,點C在以AB為邊的等邊三角形的頂點(C1)上,當點D在半圓上與點B重合時,點C與點B重合.串聯起始位置、一般位置、終止位置,進而可以猜想點C的運動路徑是以起始狀態的BC1為直徑的半圓.通過圖3,發現點D與點C的運動路徑是全等的半圓,每對對應點之間是旋轉對稱的關系,基于對應連結AD,C1C2,易證△ABD≌△C1BC2,所以∠C1C2B=∠ADB=90°,所以點C的運動路徑是以C1B為半徑的半圓.

圖3 圖4

3.2 本原性思考方向二:基于函數模型
基于函數模型的本原性思考按以下三步走.
步驟一是自主發現函數關系.世界是普遍聯系的,運動圖形中某個元素的運動變化必然帶來其他相關量的變化,函數關系是運動圖形研究的重要方向之一.通過分析本題題意、想象運動過程發現,點C隨著點D的運動而運動,即我們要研究的線段AC的長度隨著線段BD的長度變化而變化,其中蘊含著初中函數概念宏觀變量說的三個基本要素:①這是一個運動變化過程;②在這個運動變化過程中有兩個變量(線段AC與BD的長度);③一個變量(AC)隨著另一個變量(BD)的變化而變化.因此,回歸函數概念就自然聯想到問題情境中蘊含著函數關系,即線段AC與BD的長度之間存在著函數關系.
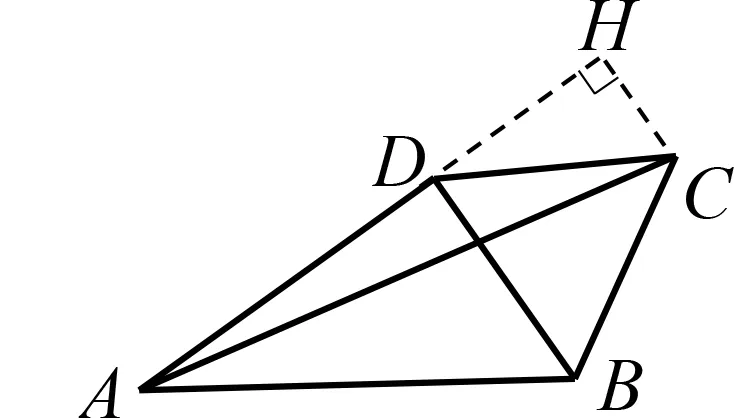
圖5
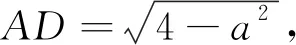
3.3 本原性思考方向三:基于圖形變換

圖6

4 本原性思考的反思
4.1 思考本原問題,引導學生學會如何想到
數學學習有三個遞進的層次:第一層次是知其然,知道是什么;第二層次是知其所以然,知道為什么;第三層次是知何由以知其所以然,知道怎么想到的[1].平時解題教學中經常會遇到這樣一種現象:學生練習時冥思苦想而不得其解,但經老師稍加提示或點撥就恍然大悟,這種“不是做不到,而是想不到”的現象問題到底出在哪里?根子出在教師在“如何想”上缺少示范和引導.套路化解題訓練將解題思考的過程濃縮成了解題套路,不利于學生感悟、學會如何想到.解題教學應重視多讓學生思考“思路是怎么想到的”這一本原性問題,教會學生學會自主尋求解決問題的思路,發展學生的創新意識和能力.
本題點A是定點,點C是動點,欲求AC的最大值一般會想到要把點C的運動路徑弄清楚,自然形成基于運動路徑的解題思路;本題分析圖形運動元素,發現點C隨著點D的運動而運動,即線段AC隨著線段BD的變化而變化,回歸函數概念自然聯想到問題情境中蘊含著函數關系,從而形成基于函數模型的解題思路;本題由線段BD與BC是共端點的相等線段的特征,引發學生自主聯系旋轉變換的特征,自然形成基于圖形變換的解題思路.這些思路是基于圖形條件和特征自然形成的,學生不僅“做得到”,而且“想得到”.
4.2 經歷思考過程,發展學生數學核心素養
《普通高中數學課程標準(2017年版)》指出:數學學科核心素養是數學課程目標的集中體現,是具有數學基本特征的思維品質、關鍵能力以及情感、態度與價值觀的綜合體現,是在數學學習和應用的過程中逐步形成和發展的.解題是數學應用的一個過程,應把解題思考的過程還給學生,讓學生在思路形成的過程中發展數學核心素養.套路化解題訓練剝奪了學生思考的過程,不利于數學核心素養的形成[2].
基于運動路徑的解題思路需要學生把握運動全過程,嘗試勾勒一些特殊位置并猜想動點運動路徑;基于函數模型的解題思路需要學生充分感受點C與點D、線段AC與BD之間的運動變化關系;基于圖形變換的解題思路需要學生根據圖形特征用圖形變換的眼光審視圖形.這些思考過程有利于學生直觀想象素養的形成.基于運動路徑的解題思路中,動點C的運動路徑需要先猜想再證明,合情推理與演繹推理有機結合,有利于學生邏輯推理素養的形成;基于函數模型的解題思路需要學生自主發現線段AC與BD之間的函數依賴關系,然后再自主構造函數模型,應用函數模型解決問題,有利于學生數學建模和數學抽象素養的形成.
4.3 反思思考過程,感悟解題通法思維大道
題型歸類和套路技巧掩蓋了解題思維的暴露和展示.解題思路的自然生成分析不夠,讓學生產生解法的獲得是“天才的靈機一動”、可遇而不可求的錯覺,不利于學生形成解題通法、感悟思維大道[2].解題通法普適性強,可遷移應用的范圍廣.思維大道是數學探究的基本思想方法,不僅適用于數學學科的學習和研究,同樣也適用于其他學科.
反思基于運動路徑的解題思路,學生容易感悟到:解題要力戒“望而生畏”,敢于從特殊到一般進行嘗試,敢于“大膽猜想,小心求證”;反思基于函數模型的解題思路,學生容易感悟到:點C與點D、線段AC與BD之間的運動變化關系蘊含著函數概念的基本屬性,回歸基本概念是解題的重要手段;反思基于圖形變換的解題思路,學生容易感悟到:圖形變換是研究幾何問題的重要視角.
5 反對套路訓練,提倡本原性思考
解題套路確實可以減少學生的思維量,提升學生的解題速度,但解題套路縮略了思考過程,放棄了思考過程所承載的育人價值,無法幫助學生解決“解題思路如何想到”的本原性困惑,數學核心素養的培育缺少土壤[3].套路往往立足于某一類題的特殊解題技巧,普適性差,題目稍有變化,學生可能就會無從下手,在反套路的評價命題趨勢下,套路訓練的收效越來越差.同時套路繁多,就比如前面提到的“瓜豆原理”,初中階段常見的類型有主動點在直線上和主動點在圓(或圓弧)上兩大類,主動點在直線上又分“線段+直線”
“角+直線”,主動點在圓上又分“線段+圓”“角+圓”,學生每掌握一種套路類型都需要大量刷題,通過大量刷題形成“條件反射”,加重了學生的課后作業負擔.因此,我們反對套路訓練.
本原性思考還原思考過程,能充分發揮思考過程所承載的育人價值,有利于解決學生“解題思路如何想到”的本原性困惑,發展學生的數學核心素養,幫助學生感悟解題通法和思維大道,從而真正提升學生的解題能力,減輕學生的課后作業負擔.因此,我們提倡給學生提供更多的本原性思考的機會.

