一道高中數學聯賽試題的多解探究及推廣

徐鳳旺 成 敏

(貴州師范大學數學科學學院 550025)

1 試題呈現

分析 這是2021年全國高中數學聯賽廣西賽區預賽的一道根式函數求值問題,此題結構簡單,形式上具有數學的美感.文[1]對此題給出了不同的解法及試題引申,筆者讀后深受啟發,于是對該題做進一步的探索,得到另外四種解法和試題變式的幾個推廣,與大家一起分享.

2 試題解析

評注 此解法在換元后借助不等式,求出函數的最大值.

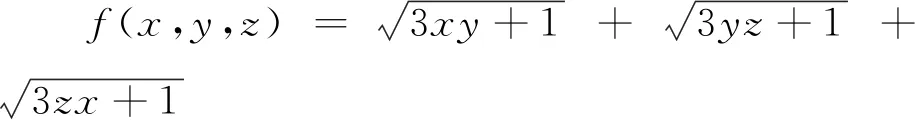
評注 此解法通過“先設后求”的思想,將問題轉化為不等式問題,再利用算術平均數和冪平均數的關系,求出函數的最大值.

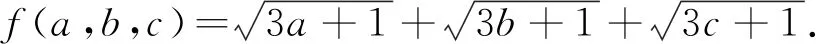
評注 此解法通過換元法將問題進行轉化,利用函數的切線性質,求得函數的最大值.

數學中的一題多解是從不同的視角出發、按照不同的思路以及不同的方法給出同一道題的解答.本文中給出四種不同的解題視角,體現了一題多解的數學解題思維,將根式函數的求值問題與不等式、切線性質等知識點結合起來,體現了轉化與化歸數學思想的重要性.

3 試題推廣

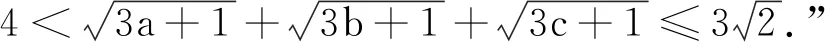
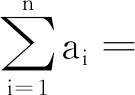
分析 將試題中的三元推廣到n元.

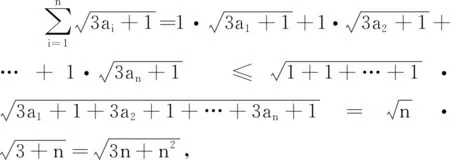
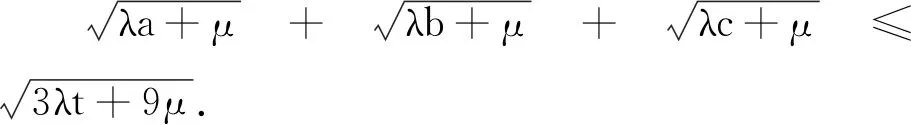
評注 將試題中的系數進行了一般化.

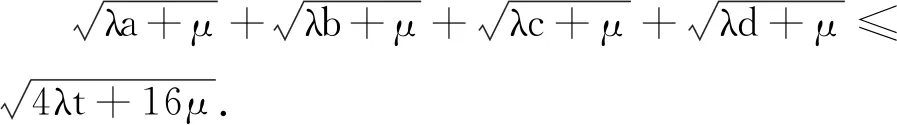
評注 將試題中的三元推廣到四元,同時將試題中的系數一般化.

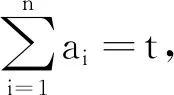
分析 將試題中的三元推廣到n元,同時將其系數一般化,求得最大值.推廣2、推廣3、推廣4均可由柯西不等式證明.下面證明推廣4,推廣2和推廣3的證明不再敘述.

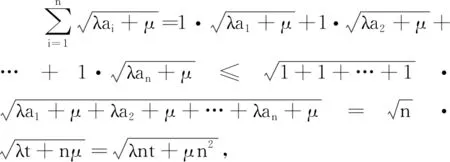
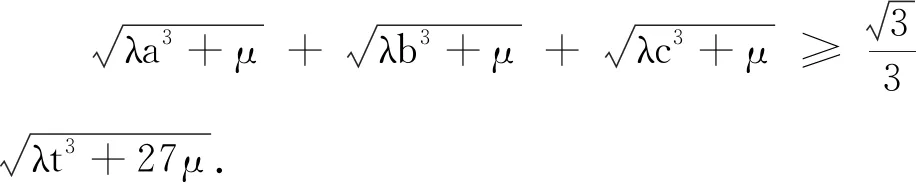
分析 通過改變試題中未知數的冪,求得不等式的最小值,可借助琴生不等式證明.

一題多解可以促進學生數學思維的發展,使得他們從不同的角度看待問題,形成發散思維;推廣是數學學習和數學研究的一種途徑,它能夠加深學生對問題的理解,使學生認清問題的本質,掌握其解題的思想方法,有效地提高解決問題的 能力.