黏土中爆炸成坑地沖擊耦合效應實驗研究*

時本軍，李 杰，郭 緯，徐天涵，徐小輝，李 干，蔣海明

（陸軍工程大學爆炸沖擊防災減災國家重點實驗室，江蘇 南京 210007）

隨著重要軍事目標的堅固化和地下化，世界各國加速發展鉆地武器，使其打擊更加精確、侵徹更深、破壞力更大，對地下防護工程帶來極大威脅。與空中爆炸或觸地爆炸相比，鉆入地下的武器再爆炸能使絕大多數爆炸能量耦合至巖土中，使地沖擊威力大大增強。同時，鉆地爆炸對地下工程產生的破壞效應與其地沖擊能量特征密切相關。大當量地下爆炸現場實測數據均表明[1-5]，地下爆炸耦合至巖土中的地沖擊能量隨裝藥埋深增加而迅速增大，在某一臨界深度時增速減緩，而后隨埋深增大逐漸趨近于地下封閉爆炸。深埋封閉爆炸的耦合地沖擊能量可達同當量觸地爆炸的10 倍以上，因此對于防護工程設計來講，必須要建立爆炸深度和耦合地沖擊能量間的定量關系。

近幾十年來，對于巖土介質中的封閉爆炸和觸地爆炸的研究已經較為完善，可獲得較豐富試驗數據和較為成熟的計算方法。梁霍夫等[6]在土壤(包括飽和土和非飽和土)、砂(包括飽和砂和非飽和砂)、巖石中進行了平面波、球面波和柱面波的地沖擊效應研究，綜合考慮現場的地質特征和實驗所用介質的物理力學參數建立了較為簡練的地沖擊效應計算方法。在不同巖土介質中地沖擊衰減規律方面，學者們也做了大量的研究工作。Yankelevsky 等[7]通過對已有實驗數據的分析和數值模擬，得到沖擊波峰值壓力衰減的特點。穆朝民等[8-9]在黃土和砂土中進行了一系列爆炸成坑試驗，并結合爆炸宏觀特征，確定了黃土及飽和砂土中發生封閉爆炸的臨界比例埋深，得到了變埋深條件下應力波在土中傳播規律。施鵬等[10]通過模擬手段計算了不同裝藥比例埋深下土中爆炸能量耦合問題，通過實驗得到了耦合系數數據，并給出了公式使用范圍和對象。葉亞齊等[11]在砂質黏土中進行了不同裝藥比例埋深爆炸自由場試驗，給出了砂質黏土中不同深度爆炸自由場地沖擊參數的衰減規律，建立了砂質黏土中不同深度爆炸自由場地沖擊參數的預計公式。趙紅玲等[12]研究了石灰巖中常規裝藥不同埋深爆炸自由場地沖擊參數的傳播規律，得到了石灰巖介質中變埋深爆炸地沖擊參數隨比例距離的預計公式。何翔等[13]基于試驗手段研究了常規裝藥爆炸不同深度對自由場直接地沖擊參數的影響，建立了石灰巖中爆炸成坑經驗公式和地沖擊傳播特性。但由于土中淺埋爆炸是復雜的耦合效應問題，其理論和實驗研究均存在諸多困難，目前尚無可靠的計算方法。目前對于淺埋爆炸地沖擊效應的計算，通常采用由美國陸軍工程兵水道試驗站給出的地沖擊耦合系數，將淺埋爆炸轉變成等效的封閉或者觸地爆炸[14-15]。然而，為驗證此方法的有效性，在飽和砂土中共進行了58 次爆炸試驗[16]，發現該計算與試驗結果存在較大偏差，特別是在爆炸遠區，預測公式不能準確求得地沖擊參數，只能定性分析。關于地沖擊耦合系數的計算，目前尚無準確的計算方法，給出的實驗數據誤差較大，難以適應鉆地爆炸等效當量及耦合地沖擊參數的準確計算。同時，現有文獻[17-18]中存在多種“地沖擊耦合系數”，如能量耦合系數、等效當量系數、地沖擊應力耦合系數等，相互間未建立準確的換算方法，若不仔細區分其物理本質而加以混淆使用，容易造成計算錯誤。

為了研究黏土中爆炸成坑體積與耦合地沖擊能量的關系，本文在已有研究成果的基礎上，系統開展不同埋深下成坑地沖擊耦合效應實驗研究，探索彈坑體積以及地沖擊壓力隨裝藥埋深增加的變化規律，尋找不同耦合系數間的換算關系以及等效封閉當量計算方法，以期為地下工程的抗爆防護提供設計依據。

1 實驗介紹

1.1 黏土試樣

本實驗所用的黏土取自南京孟墓地區，首先清除地表覆土，然后將黏土平攤放置地表撿去里面大塊雜質，之后倒入爆炸試驗容器中，分層夯實。該黏土中主要化學組成及質量分數分別為：SiO2(61.16 %)、Al2O3(23.10 %)、Fe2O3(8.94 %)、K2O (2.65 %)、MgO (1.56 %)，等。黏土試樣的密度是2.242×103kg/m3，含水率12.8 %，縱波速度1832 m/s，其波阻抗近似為0.4×107N?s/m3。根據國家標準[19]采用篩析法計算繪出黏土的粒徑級配曲線如圖1 所示。

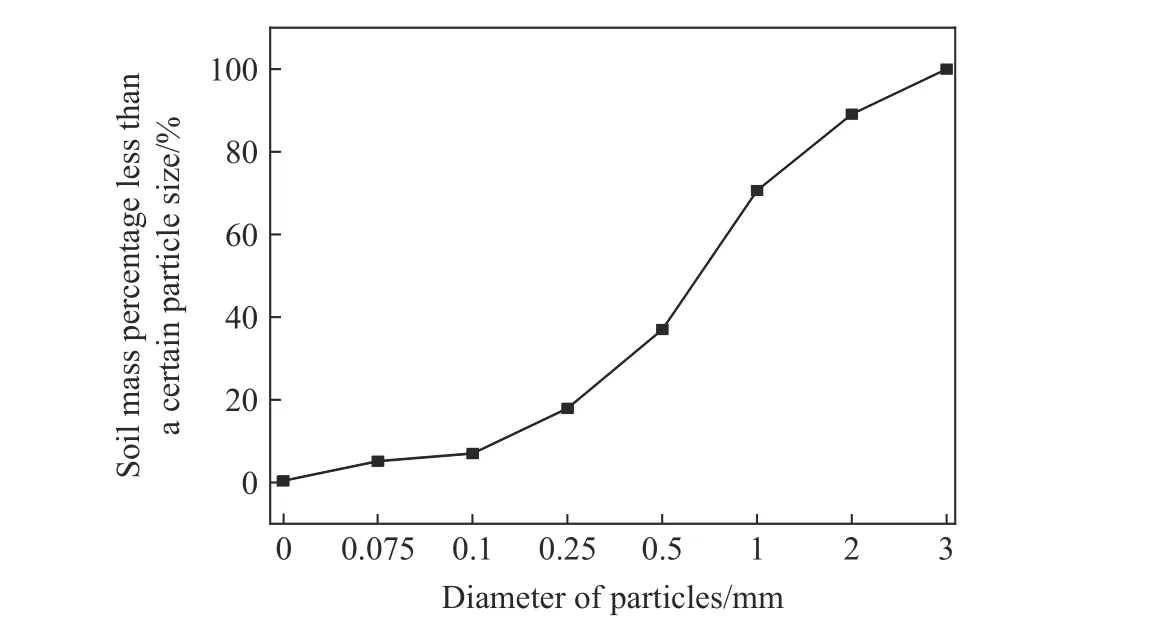
圖1 黏土的粒徑級配曲線Fig.1 Particle size gradation curve of clay

1.2 爆炸容器及球形爆源

采用一種分層可拼裝的筒體結構作為爆炸容器，如圖2 所示。該裝置高度是1 490 mm，容器內徑1 500 mm，鋼板厚度為15 mm，由7 個子單元自下而上垂直拼裝而成。子單元由Q345 鋼板經彎、卷、焊等工序加工而成，包括上下兩片寬75 mm、厚16 mm 的法蘭盤，起到提高容器半徑法向剛度和連接拼裝單元的作用。法蘭盤上均勻加工24 個內徑16 mm 的通孔，為增強法蘭和圓環之間的強度，在圓環外側鋪設12 個肋板。子單元之間通過強度等級為8.8 級的高強度M14 螺栓連接。按照薄壁圓筒公式計算，容器可承受內壁上強度為5.2 MPa 的均勻荷載。

圖2 分層式爆炸容器Fig.2 Layered explosion vessel

在黏土介質爆炸實驗研究中，大多使用塊狀TNT、雷管和乳化炸藥，當測點距離爆心較遠時，可以把爆源近似當作點源，但是測點距離爆心較近時，炸藥的形狀、密度和種類均會給試驗結果產生顯著的影響，Krauthammer[20]指出在爆炸試驗中采用球形裝藥所采集的試驗數據更加科學。為獲取爆心距較近范圍內黏土中的爆炸應力波衰減規律，本實驗選用球形裝藥作為爆源，如圖3 所示。藥球由三硝基甲苯（TNT）采用一體成型技術壓裝而成，藥球質量為10.5 g，直徑為24.4 mm，裝藥密度1.5 g/cm3。藥球頂部預留直徑8 mm、深度12 mm 的雷管安裝孔，其尺寸和標準雷管中猛炸藥尺寸相近，安裝孔的體積占比約為7.93 %。采用電雷管起爆，實驗前將雷管插入裝藥安裝孔中，并使用絕緣膠帶固定。

圖3 球形爆源Fig.3 Spherical explosion source

1.3 測點布置

為獲取裝藥埋深對地沖擊壓力傳播衰減的影響規律，共設計7 組不同埋深的爆炸實驗，每組實驗中布置5 組測點（記為1#、2#、3#、4#、5#），各實驗裝藥埋深（h）和地沖擊壓力測點比例爆心距（R）見表1。

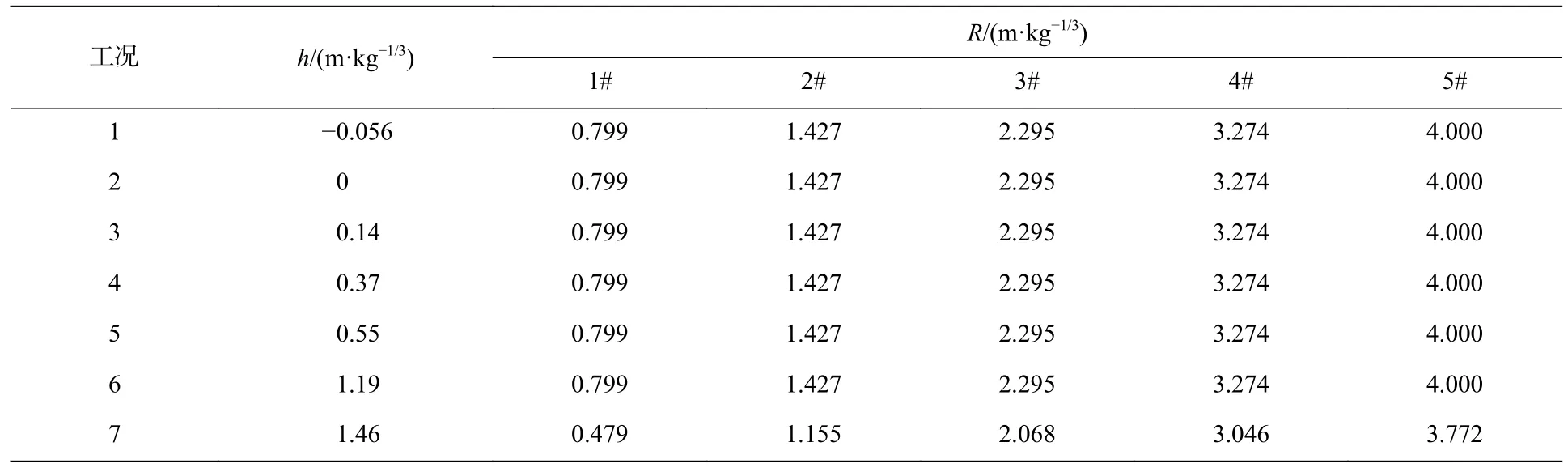
表1 裝藥埋深（ h ）及爆心距（ R ）設計Table 1 Design of burial depth of charge ( h ) and burst core distance ( R )

藥球位于筒體容器的中軸線上，在試樣制備過程中預留裝藥孔，然后將藥球放入裝藥孔后回填。爆心下方共鋪設5 層土壓力傳感器，每層鋪設2 個，于中軸線兩側對稱布置，距離容器軸線50 mm，具體如圖4(a)所示。采用DNS123 型土壓力傳感器獲取不同測點處爆炸波法向應力的時程曲線，其尺寸為?50 mm×10 mm，如圖4(b)所示。為了減少傳感器本身對地沖擊傳播的干擾，采用上下層交叉鋪設的方式使傳感器位于不同方位，交叉角度約36°，如圖4(c)所示（圖中編號表示傳感器鋪設所在的層數）。采用東華DH8302 高性能動態信號測試系統進行地沖擊壓力數據采集，采樣頻率為100 kHz，如圖5所示。

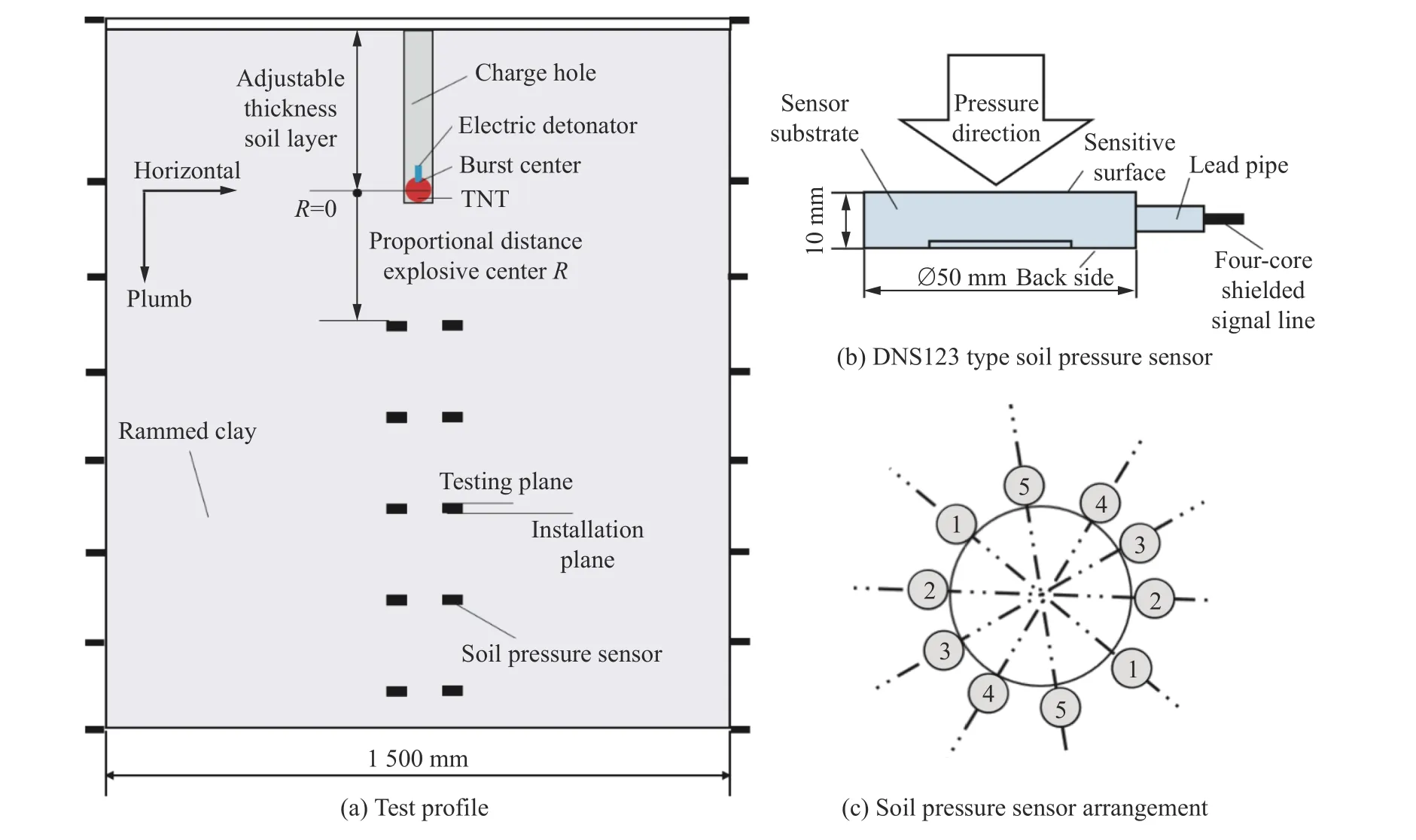
圖4 藥球位置及傳感器布置Fig.4 Drug package location and sensor arrangement

圖5 測量采集記錄圖Fig.5 Measurement acquisition record diagram

為方便對比不同裝藥埋深對地沖擊傳播的影響，7 次實驗中保持各組傳感器距離爆心的比例距離不變。每做完一次實驗后首先利用3D 掃描儀對彈坑進行掃描，然后沿彈坑中軸面將彈坑剖開，觀察彈坑周圍介質的壓縮破壞情況，分析完成后將破壞的黏土鏟除而后重新鋪設新的黏土層并進行重新夯實。

2 實驗結果分析

2.1 成坑特征

2.1.1 可視彈坑分析

黏土中爆炸時，爆炸沖擊波和爆生氣體壓縮爆炸中心周圍黏土介質，并形成沖擊波向四周傳播，隨著傳播距離增加，沖擊波逐漸衰減為塑性波、彈性波，同時在黏土介質中形成爆炸空腔區、破壞區等區域。當沖擊波遇到自由面時，在自由面反射作用下形成反向傳播的拉伸波，對黏土介質產生層裂或者剝離。如果爆炸埋深較淺，爆轟產物和爆炸應力波激發近地表土層土顆粒發生飛散形成拋擲彈坑；而隨著埋深進一步增大，彈坑體積也進一步增大，直至在某一最佳臨界深度處體積達到最大；而后隨著埋深進一步增加，地表可視彈坑逐漸消失，地下逐漸形成完整的爆炸空腔，但由于空腔膨脹作用，在地面處形成鼓包和破裂；最后，當埋深超出封閉爆炸臨界深度時，地下爆炸破壞效應完全被封閉在地下，地表無反應，一般將地表面上無明顯可見變化的深度稱為封閉爆炸臨界深度。圖6 和圖7 給出了不同埋深情況下爆炸彈坑的宏觀破壞情況，相關彈坑尺寸數據見表2。從結果可知：可視彈坑，在裝藥埋深達到0.55 m/kg1/3時，彈坑體積達到最大，在裝藥比例埋深到1.19 m/kg1/3時，地表彈坑幾乎將近消失，同時地表發生明顯隆起鼓包(圖6(c)和圖7(c) )，當比例埋深達到1.46 m/kg1/3時，地表鼓包幾近消失，但在土層表面形成不規則裂紋(圖6(d)和圖7(d) )。對于封閉爆炸臨界深度，目前公開文獻的外觀點基本一致，穆朝民等[8]所做的土中爆炸試驗指出在比例埋深到達1.96 m/kg1/3時，地表面接近沒有明顯可見變化，梁霍夫[6]在歸納整理的資料中，也得出土中集團裝藥封閉爆炸臨界深度為2.0 m/kg1/3。

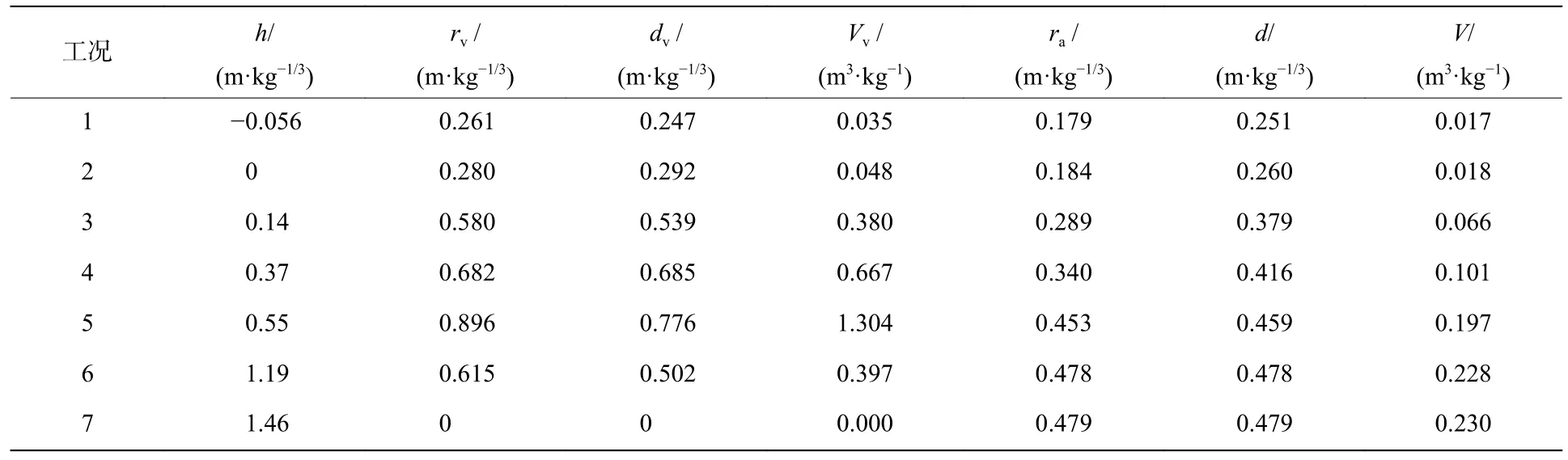
表2 不同埋深條件下彈坑尺寸數據Table 2 Size data of craters under different burial depths

圖6 成坑的俯視與剖面圖Fig.6 Overhead view and profile of the crater

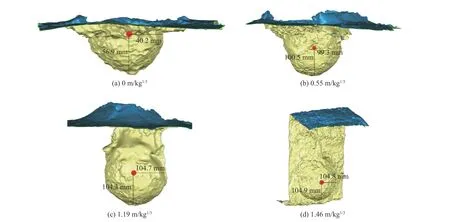
圖7 3D 掃描成坑形貌Fig.7 3D scanning into crater morphology

圖8 為ConWep 爆炸荷載計算程序[21]預測的質量為10.5 g TNT 藥球在黏土中可視爆坑的深度和直徑隨裝藥比例埋深變化曲線，及其與本文實測結果的對比。在裝藥比例埋深h≤0.55 m/kg1/3時，可視爆坑深度實測值和ConWep 計算程序預測的值偏差最高可達20.6 %，而實測的可視爆坑直徑與ConWep 預測值具有很好的一致性，可視爆坑深度產生的偏差可能由于夯實的黏土起炸后，飛散的黏土粘連并帶出爆坑里面黏土，回填變少，現場實測的可視爆坑比ConWep 中預測的可視爆坑要大。

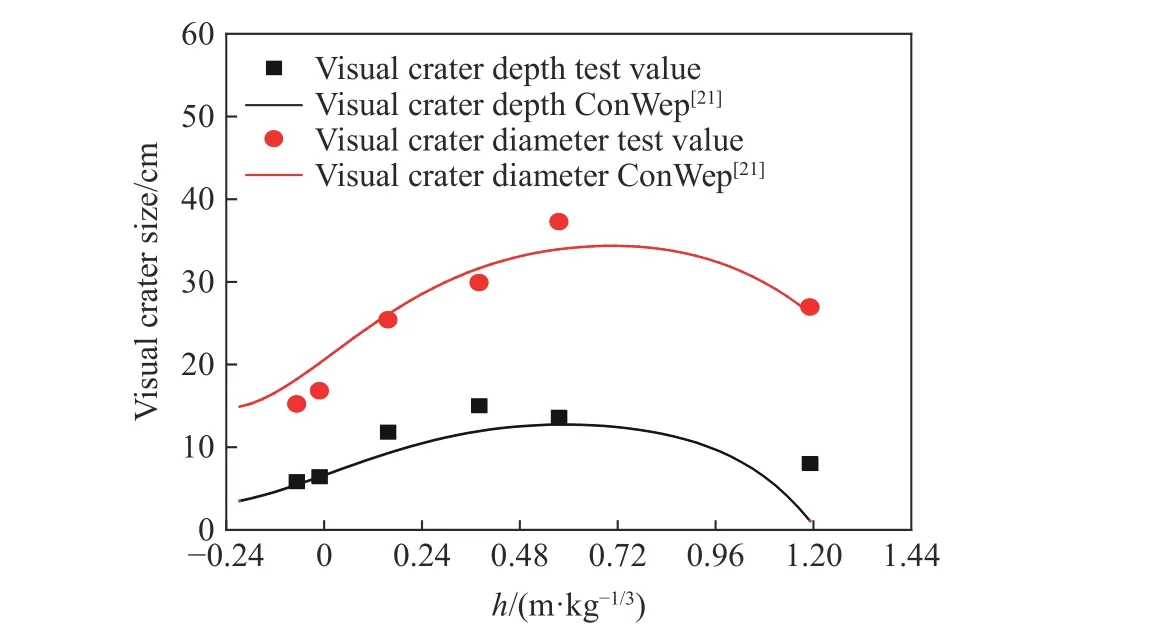
圖8 可視彈坑實測值與ConWep 計算值的對比Fig.8 Comparison of the measured values of the visible burst crater with those computed by ConWep

2.1.2 有效彈坑分析

裝藥爆炸過程中，裝藥爆生產物通過壓縮周圍介質形成地沖擊波，裝藥中心下方的壓縮彈坑對于應力波的形成具有重要作用，將裝藥中心下方的壓縮彈坑稱為有效彈坑。理論分析表明[22]：耦合至巖土中的地沖擊能量與有效彈坑體積呈正比例關系，在以往歷史試驗數據中，往往只關注可視彈坑，而忽略了有效彈坑體積的統計。為了便于描述有效彈坑的演化過程，不妨引入球形度和有效彈坑體積比兩個量；其中，球形度是有效彈坑半徑ra與彈坑深度d的比值。有效彈坑體積比是不同裝藥比例埋深下的有效彈坑體積V與工況7 有效彈坑體積V7的比值，其比值記為V/V7。可通過表2 數據計算得到有效彈坑的球形度和有效彈坑體積比。圖9 給出了隨裝藥埋深增加有效彈坑球形度和有效彈坑體積比值的變化規律。當裝藥比例埋深為h=0 時，有效彈坑輪廓呈拋物線型（圖6(a)），裝藥中心所在的球形度約為0.708；隨裝藥埋深增大，有效彈坑的球形度和體積比均在增加（圖9），同時爆心下方彈坑輪廓線逐漸由拋物線型演化為半球形（圖6(b)～(d)）；當裝藥比例埋深h≥0.55 m/kg1/3時，裝藥中心下方有效彈坑體積達到趨近于極限，其形狀也接近于完全封閉爆炸。

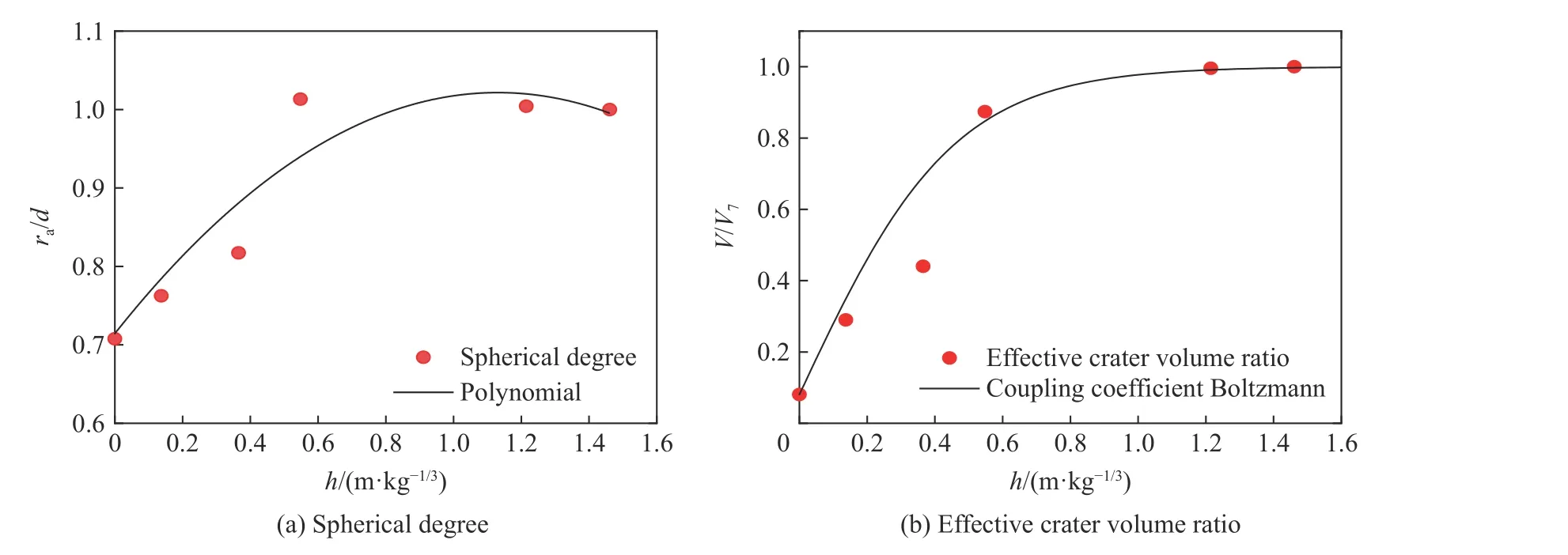
圖9 隨裝藥埋深增加有效彈坑的變化規律Fig.9 The change rule of effective crater with the increase of charge depth

2.2 地沖擊傳播規律特征

圖10 分別給出了裝藥比例埋深為0.55 m/kg1/3（工況5）和1.19 m/kg1/3（工況6）時，不同測點處的地沖擊應力實測波形，從圖10 中可以看出，隨距離裝藥比例距離的增加，地沖擊應力峰值呈指數衰減特征。

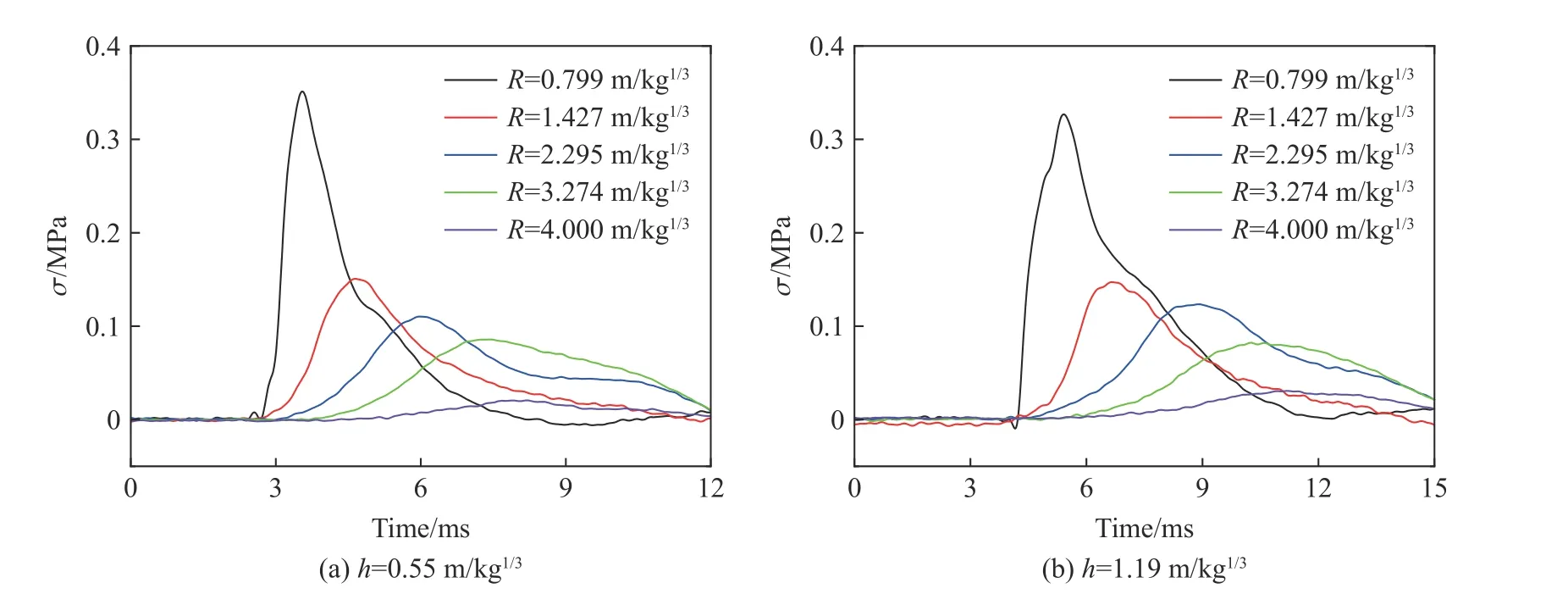
圖10 不同裝藥比例埋深時實測地沖擊應力波形Fig.10 Measured stress waveform of clay at different scaled buried depths

表3 給出了不同裝藥埋深情況下地沖擊應力峰值統計數據，圖11 給出了不同比例爆心距離處地沖擊應力峰值比值隨裝藥比例埋深增加的變化情況，地沖擊應力峰值比值是不同裝藥比例埋深下爆炸應力峰值σpk與工況7 下爆炸應力峰值σpk7的比值。從表3 和圖11 中可以看出，在相同比例爆心距離處，當裝藥比例埋深h≤0.55 m/kg1/3時，隨裝藥埋深增加，耦合至黏土中的地沖擊壓力峰值也急劇增大，而當裝藥比例埋深h≥0.55 m/kg1/3時，耦合至黏土中的地沖擊壓力峰值增勢趨近平緩，接近于完全封閉爆炸，這一變化趨勢與有效彈坑體積隨裝藥埋深的變化趨勢(圖9(b) )基本一致。

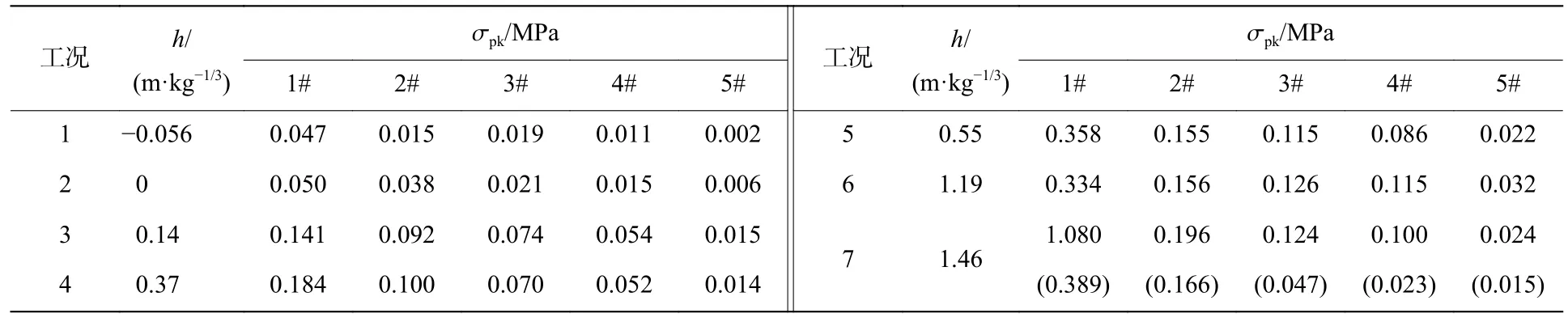
表3 黏土中各比例埋深下地沖擊應力峰值數據Table 3 Subsurface impact stress peak data of each proportion buried depth in clay

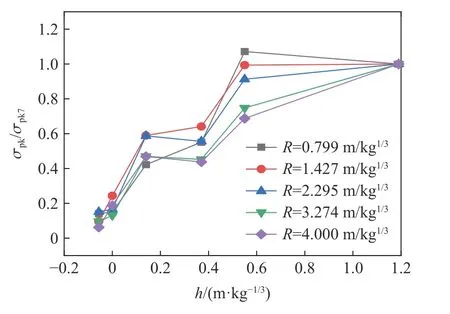
圖11 不同比例爆心距離處地沖擊應力峰值比值隨裝藥比例埋深增加的變化情況Fig.11 Peak of the ground impact stress varied with scaled butied depth charge at different scaled blast center distances

將爆炸地沖擊應力峰值接近于封閉爆炸時的爆炸比例埋深稱為等效封閉爆炸臨界埋深，可知等效封閉爆炸臨界埋深與封閉爆炸臨界埋深為兩個不同概念：對于土中化學爆炸，當裝藥埋深與封閉爆炸空腔半徑相當時，漏斗坑位于裝藥中心以下的部分呈半球型，半徑與封閉爆炸半徑基本相同，此時地下爆炸輻射至地下的地沖擊參數基本不受來自地表的影響，介質中爆炸壓縮波的幅值與完全封閉爆炸產生的幅值幾乎接近，因此可以將封閉爆炸空腔半徑作為等效封閉爆炸臨界埋深。

對于巖土體介質中爆炸，目前一致認為可以利用公式σ=A(r/Q1/3)?n描述地沖擊應力傳播的衰減規律；其中：A和n分別為應力經驗表達式的衰減系數和衰減指數；r為爆心距，單位m；Q為炸藥質量，單位kg。圖12 給出了不同裝藥比例埋深條件下，地沖擊壓力傳播衰減曲線，表4 給出了對于的A、n值。衰減指數n反映了隨爆心比例距離的增加地沖擊傳播的衰減規律，只與巖土體介質的物理力學性質相關，與裝藥埋深無關。為了上述公式簡潔性，對不同裝藥比例埋深條件下衰減指數n求平均值，其平均值記為，可得實驗所用黏土的地沖擊傳播平均衰減指數為1.14。衰減系數A則反映了隨裝藥埋深增加耦合至巖土中的地沖擊應力的變化規律；將平均衰減指數為1.14 條件下的不同比例埋深的衰減系數記為A′，從表4 可以看出，當裝藥比例埋深h≥0.55 m/kg1/3時，隨裝藥埋深增加，A和A′值變化均趨近平緩，進一步說明對于黏土，可將h≈0.55 m/kg1/3作為等效封閉爆炸臨界埋深。

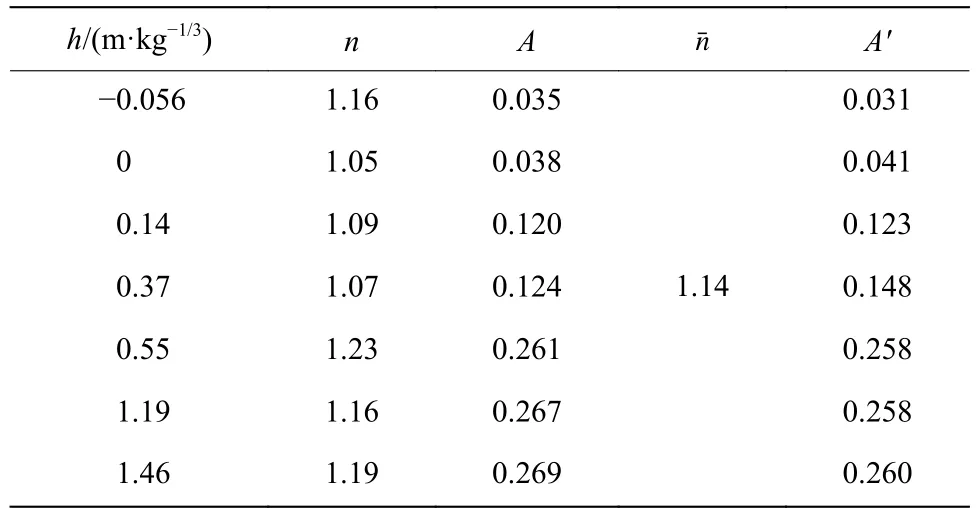
表4 不同裝藥比例埋深條件下擬合參數Table 4 Fitting parameters with different scaled buried depths of charge

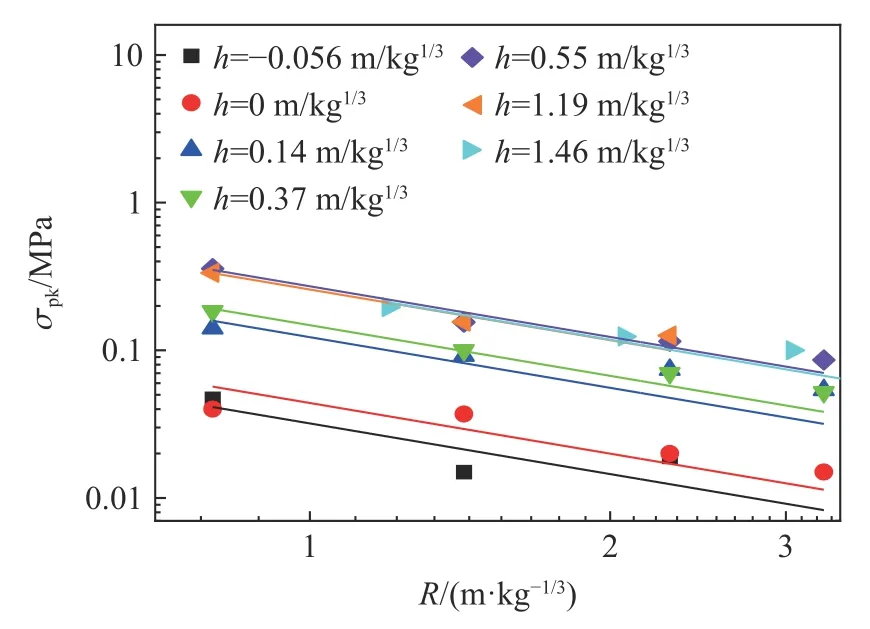
圖12 不同裝藥比例埋深時地沖擊應力峰值衰減曲線Fig.12 Peak groud impact stress attenuation with scaled blast center distance at different scaled buried depths of charge

3 成坑地沖擊耦合規律分析與等效當量計算

3.1 成坑與地沖擊耦合規律理論分析

巖土介質中發生爆炸時，爆炸空腔中的爆轟產物擠壓四周的巖土介質擴張，并形成沖擊波向外傳播，耦合進介質中的能量可以通過壓縮邊界（非彈性變形區邊界）徑向力沿邊界位移所做的功進行計算，有約一半的能量變為動能[23]：

式中：Sr為半徑為r的球形表面積，ur為r處巖土的徑向位移，ur(∞)時間趨于無窮的最終位移大小，σr為r處的徑向應力。

文獻[24-25]給出了封閉爆炸和觸地爆炸時從彈性邊界傳播出的能量，推導發現對于淺埋爆炸而言，彈性區邊界處傳播出的能量Wfailure依然由彈性邊界所包圍的破壞區巖體體積V*所控制，即Wfailure與V*呈線性關系：

式中：cp為介質中縱波速度，cs為介質中剪切波速，τs為剪切強度，G為剪切模量，B=[5+3(1+24υ)2]/64取決于爆源周圍巖石介質的性質，υ為巖土介質的泊松比。

圖13 給出了依據爆炸成坑最終形態巖土介質中爆坑常見的三種形式。對于地下爆炸，從裝藥中心傳播出的地沖擊能量向四周傳播，但對防護工程而言一般均處于裝藥中心下方。對于有效的地沖擊能量，通常只考慮裝藥中心以下的半空間范圍，因此在本文中所述的地沖擊能量均指有效地沖擊能量。

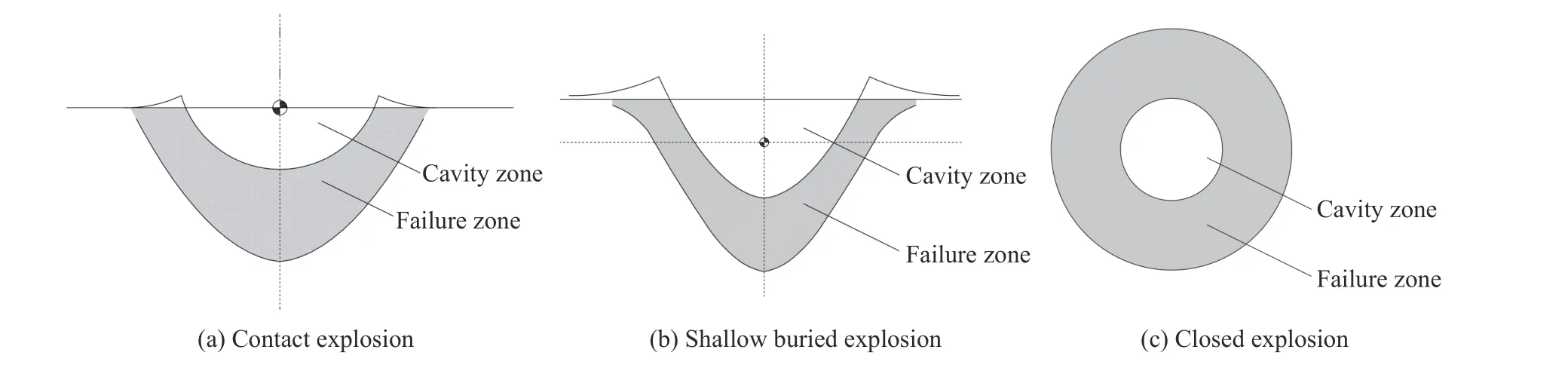
圖13 地下爆炸的三種形式Fig.13 Three types of underground explosion

耦合入巖土介質中的地沖擊能量源自于爆炸空腔擴張壓縮做功，當爆炸空腔擴張停止后，爆炸產生的能量耦合入介質的過程基本結束。根據已有的數據發現，可以用Boltzmann 函數來表達爆炸地沖擊能量耦合系數ηe(h) 變化規律，結合函數的特點，只要分別求出觸地爆炸和封閉爆炸的能量耦合系數（ηe(0)和ηe(∞)），即可描繪能量耦合系數的發展規律：

式中：D1為觸地爆炸時的能量耦合系數，即 ηe(0)=D1；理論上，埋深為無限大時，h→∞，ηe→1，通過本實驗發現，存在著最小封閉爆炸的最小比例埋深，該值與D2相關聯，決定著曲線的發展軌跡，可取ηe=0.99時，當作封閉爆炸能量完全耦合。當裝藥比例埋深大于等效封閉爆炸臨界埋深時，傳入巖土介質中下方的有效地沖擊能量已達到飽和，本文中選取h= 1.19 m/kg1/3作為參考點，代入式(3)中可得：

根據表2 數據得：

代入式(3)，得到地沖擊能量耦合系數 ηe(h) 曲線如圖14 所示。

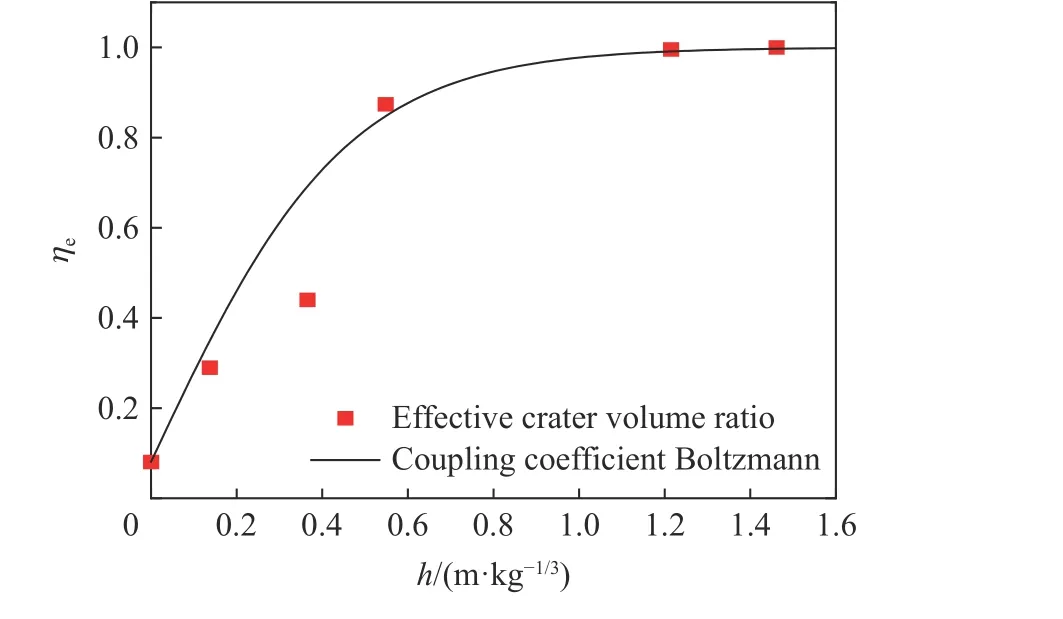
圖14 地沖擊能量耦合系數隨比例埋深的變化Fig.14 Variation of ground impact energy coupling coefficient with scaled burial depth

對于相等的爆炸當量地下爆炸，在裝藥比例埋深h=1.19 m/kg1/3，爆炸地沖擊能量W超出觸地爆炸地沖擊能量W0的倍數為：

3.2 淺埋爆炸等效當量耦合系數與地沖擊參數應力/粒子速度耦合系數

對于封閉爆炸，質點峰值速度計算公式為：

式中：Kv為地沖擊質點峰值速度經驗表達式的衰減系數，Kv與n均可由實驗得到；vpk為質點峰值速度；σpk為峰值應力；ρ 為介質密度；Q為藥球當量；cp為縱波波速。

對于淺埋爆炸，實際計算時采用當量耦合系數或地沖擊應力耦合系數將淺埋爆炸變為等效的封閉爆炸或者觸地爆炸，即利用式(8)和(9)進行求解。

當量耦合系數 ηQ為在同種介質中，比例爆心距相等時產生相同地沖擊參數(應力、速度、加速度等)大小的封閉爆炸與淺埋爆炸的當量比值，即為：

式中：Q為裝藥比例埋深為h的爆炸當量；Qeff為等效的封閉爆炸當量。

地沖擊參數應力耦合系數 ησ為在同種介質中，爆炸當量和比例爆心距均相等時淺埋爆炸地沖擊參數與封閉爆炸地沖擊參數比值，即為：

式中：σ、v、a、u分別為地沖擊應力、粒子速度、加速度以以及介質位移，下標close 表示封閉爆炸。

由此，對于淺埋爆炸，地沖擊質點峰值速度可表達為

于是得到 ησ與 ηQ的對應關系：

為準確計算淺埋爆炸等效封閉當量，還需要建立當量耦合系數與能量耦合系數間的關系。對于地下爆炸，距離裝藥中心為r處介質最大質點徑向速度的表達式為：

式中：v?為 破壞邊界處粒子速度，r?為破壞邊界與裝藥中心距離。

對于封閉爆炸，裝藥中心下方破壞區呈半球形，且有r?=kQ1/3，式(12)可改寫為：

式中：Kv=v?kn，k為 破壞區半徑比例系數，和巖土介質的力學性質有關。

就巖土介質中的淺埋爆炸，裝藥中心下方破壞區截面邊界為拋物線型，如圖13(a)和圖13(b)所示，可定義裝藥中心下方破壞區豎直高度為破壞區水平半徑的 λ (h) 倍，隨著h變大，λ (h)接近于1，即隨著裝藥比例埋深的變大，裝藥中心下方破壞區的輪廓由拋物線形漸變為半球形，如圖13(c)。如果按破壞區體積進行等效，即將淺埋爆炸破壞區體積等效為封閉爆炸破壞區體積：利用式(13)，進行地沖擊粒子速度計算，則對于裝藥中心正下方：

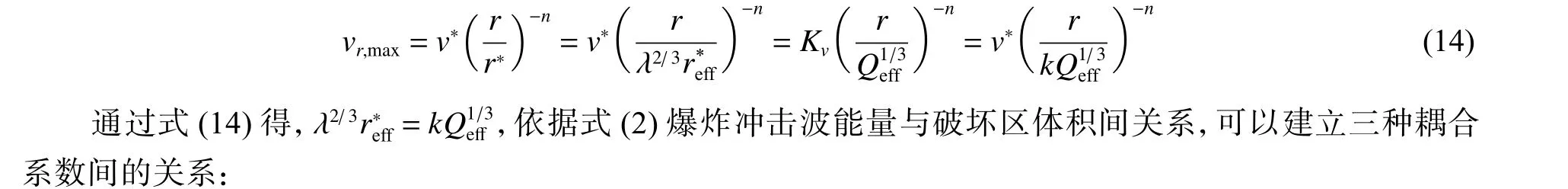
3.3 黏土中化學爆炸地沖擊應力參數耦合系數和當量耦合系數

由計算而來的 ηe，依據式(15) 計算地沖擊參數應力耦合系數ησ，結果如圖15(a) 所示，其中n取1.14。計算得到 ησ并與實測值對比，如圖15(a)所示。從圖15(a)中可以看出，地沖擊參數應力耦合系數ησ計算值與地沖擊粒子速度實測值整體上吻合度較好。與TM5-855-1[2]地沖擊參數應力耦合曲線和施鵬[10]根據數值模擬得到的曲線進行比較，可以看出，本實驗黏土的地沖擊參數應力耦合系數 ησ起點較施鵬[10]數值計算的數據較相近，當裝藥比例埋深增加到0.40～0.60 m/kg1/3之間時，地沖擊參數應力耦合系數ησ和施鵬[10]數值計算曲線符合度高，之后隨著裝藥比例埋深的增加，地沖擊參數應力耦合系數 ησ逐漸趨近1，從而也驗證了利用有效彈坑體積計算地沖擊耦合系數的可行性與可信性，在工程方面偏向安全。

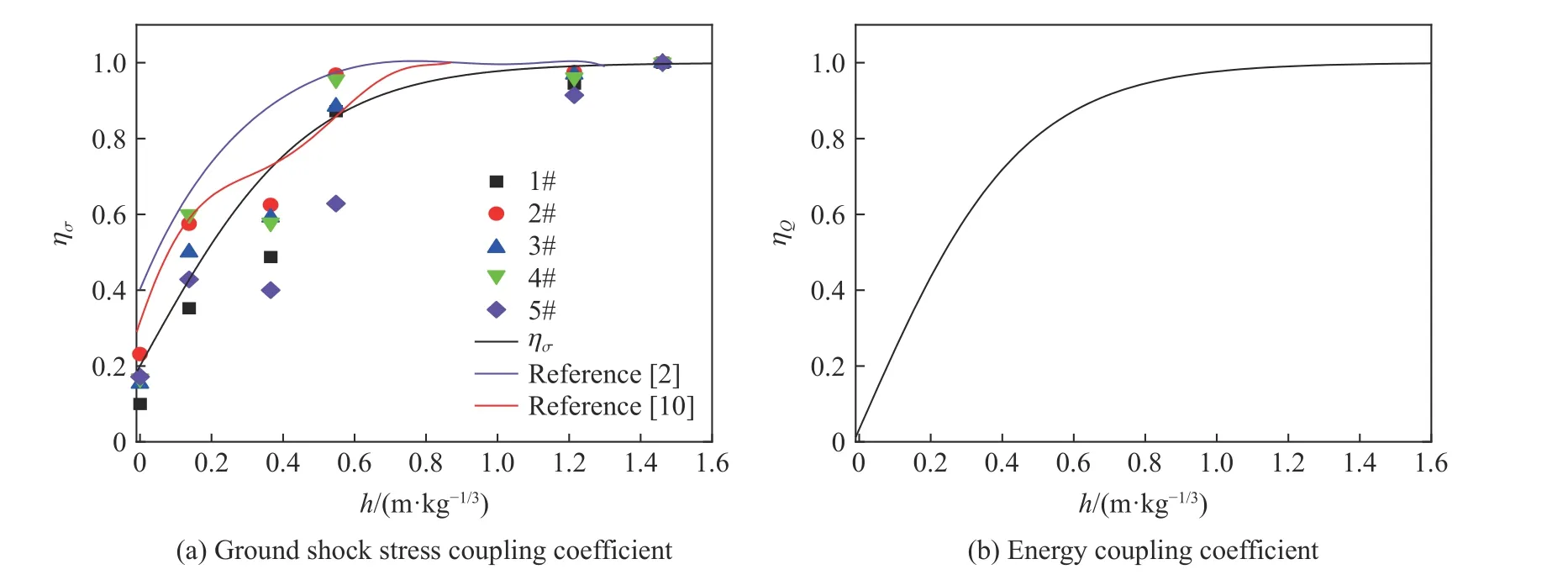
圖15 黏土中耦合系數隨裝藥比例埋深變化關系Fig.15 Relationship between coupling coefficient and scaled burial depth in clay

圖15(b)中當量耦合系數 ηQ同樣是由式(15)換算而得，隨著裝藥比例埋深的增加，當量耦合系數ηQ先快速增加，裝藥比例埋深增加到0.55 m/kg1/3后，當量耦合系數 ηQ增加變得緩慢，最后逐漸趨近于1。為便于實際工程應用，將圖15(b)中黏土當量耦合系數表達成如下關系：

4 結 論

通過在 ? 1500 mm×1490 mm 分層式爆炸裝置開展了變埋深黏土中爆炸實驗，利用3D 掃描儀和預埋土壓力傳感器分別測得不同埋深的彈坑尺寸和爆炸沖擊應力，從現場實驗和理論分析給出了彈坑壓縮體積與耦合地沖擊能量之間關系，得到如下結論：

(1) 地下爆炸發生后，隨著埋深增加，有效彈坑輪廓逐漸由拋物線型發展為半球型，其形狀演化過程與地沖擊耦合過程同步；黏土的等效封閉爆炸臨界埋深約為0.55 m/kg1/3，數值上略大于地下封閉爆炸空腔半徑，與Conwep 計算程序預測的值基本一致；通過黏土中可視彈坑演化過程可知，黏土的封閉爆炸臨界埋深約為1.46 m/kg1/3；

(2) 對于本實驗中的黏土，當?0.056 m/kg1/3≤h≤0.37 m/kg1/3，埋深增加對爆炸效應有加強的作用；在h≥0.55 m/kg1/3時，埋深增加，衰減系數處于穩定狀態，爆炸地沖擊基本完全耦合，埋深再增加爆炸耦合地沖擊能量此時可忽略；

(3) 爆炸耦合進介質中能量正比于有效彈坑的體積，此結論適用于淺埋爆炸和封閉爆炸；對于淺埋爆炸，可以把不規則輪廓通過等效面積轉化為規則的球體進行計算；黏土爆炸實驗證實了通過有效彈坑體積方式計算地沖擊耦合系數的可行性與可信性；

(4) 建立了三種地沖擊耦合系數的關系，最終都可與有效彈坑體積建立聯系，引入Boltzmann 函數給出了黏土耦合系數與比例埋深的關系；為了便于實際工程應用，文中直接給出了黏土的當量耦合系數與比例埋深的函數關系，此公式具有較好的預估精度。