變工況下半主動懸置系統滑模控制特性分析
張明亮,李 祥,李 嵐,潘道遠
(1.安徽工程大學 機械工程學院,安徽 蕪湖 241000;2.亞新科噪聲與振動技術(安徽)有限公司,安徽 寧國 242300)
0 引言
隨著生活水平的不斷提高,人們對車輛的NVH性能有了更高要求。發動機半主動懸置系統具有結構簡單,成本低、能耗少等優點,得到學術界越來越多的關注[1-3]。鄧召學等[4]設計了一種基于流動模式的磁流變懸置,并在啟停工況下進行了隔振性能試驗,改善了車輛的平順性。針對混合動力汽車啟停時產生的扭矩突變,王道勇等[5]基于懸置系統的設計方法開發了一種半主動阻尼拉桿用于減小發動機啟停時的振動。為了提高發動機半主動懸置系統的隔振性能,申玉瑞等[6]提出了一種PID控制方法,并利用改進果蠅優化算法對控制參數進行優化。潘道遠等[7]提出了一種SOA優化PID控制方法,結果表明系統采用該方法后具有良好的隔振效果。但以上控制方法均存在應用工況單一、抗干擾能力較差等問題。
滑模控制在受到參數攝動和外部干擾時具有不變性,在工程領域應用較為廣泛[8]。支敬德等[9]提出了一種模糊滑模控制用于撓性航天器姿態機動控制,仿真結果表明該控制方法能夠有效抑制附件的抖振。呂振鵬等[10]設計了一種滑模控制器用于汽車半主動座椅懸架控制,仿真結果表明該控制方法具有良好的隔振效果。為了精確控制空氣懸架的高度,尹航等[11]提出了一種基于雙死區設計的滑模控制方法,并通過仿真驗證了控制策略的有效性。滑模控制在車輛懸架系統中的應用日趨成熟[12-14],而在發動機懸置系統中的應用鮮有研究報道,這是因為發動機懸置系統的激勵頻率高、振幅小,且設計空間較小等因素造成。汽車芯片的飛速發展,為滑模控制在發動機懸置系統中的應用提供了可能性。
基于此,本文建立1/4半主動懸置系統力學模型,引入誤差動力學模型進行滑模控制器的設計。考慮車輛在行駛過程中切換擋位以及加減速等變工況的影響,建立半主動懸置系統仿真模型驗證滑模控制的有效性,為滑模控制在半主動懸置系統中的應用提供理論基礎。
1 半主動懸置系統建模
1.1 懸置系統力學模型
由于半主動懸置系統是一個非線性時變的復雜系統,為了簡化求解過程和降低計算量,建立1/4半主動懸置系統力學模型用于控制研究,如圖1所示。圖1中:me和mb分別為發動機等效質量和車身等效質量,k1和k2分別為半主動懸置等效剛度和懸架等效剛度,ce和cb分別為半主動懸置等效阻尼和懸架等效阻尼,z1和z2分別為發動機位移和車身位移,fe為發動機激勵,fc為半主動懸置的可控阻尼力。
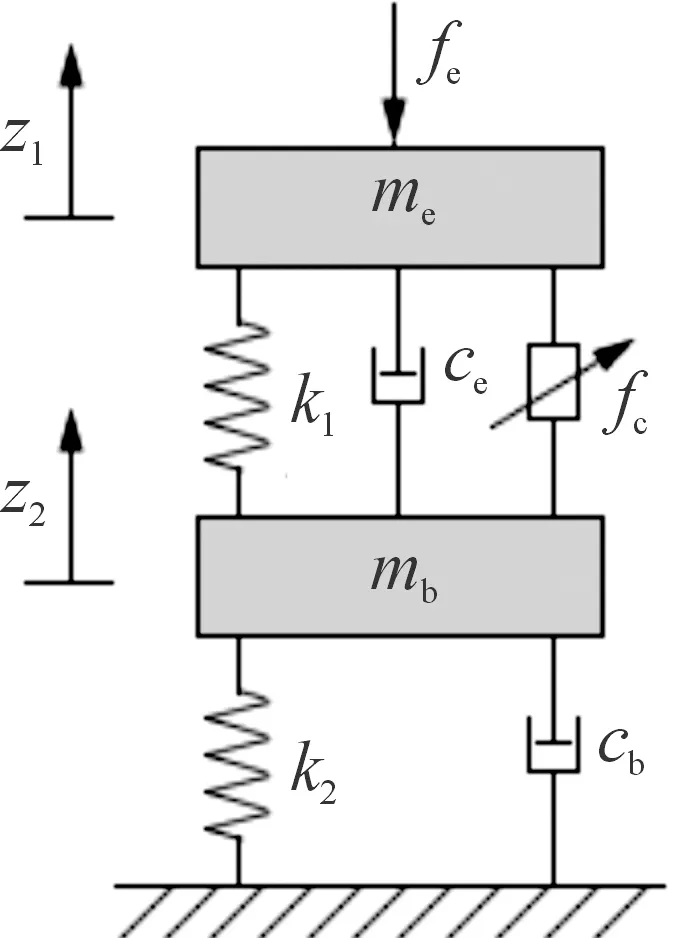
圖1 半主動懸置系統力學模型
根據牛頓第二定律對圖1中me和mb進行受力分析,定義垂直向上方向為正方向,得到系統動力學方程為
(1)
(2)
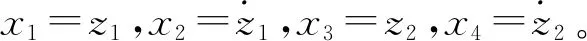
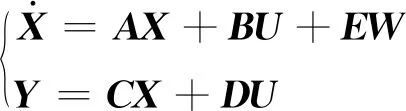
(3)
式中:X為狀態變量;A為狀態矩陣;B為輸入矩陣;U為控制矩陣;E為擾動輸出矩陣;W為擾動輸入矩陣;C為輸出矩陣;D為狀態反饋矩陣。
整理得到各矩陣分別為
W=[fe],U=[fc]
1.2 天棚阻尼參考模型
Karnopp教授于20世紀70年代初提出天棚控制理論。天棚控制是一種主動控制策略,其控制性能優越,具有良好的魯棒性。為獲取理想的輸出響應,采用一種改進的天棚阻尼懸置系統作為參考模型,如圖2所示。圖2中:csr和ctr分別是天棚阻尼參考模型的阻尼系數,z1r和z2r分別是天棚阻尼參考模型中發動機和車身的位移。
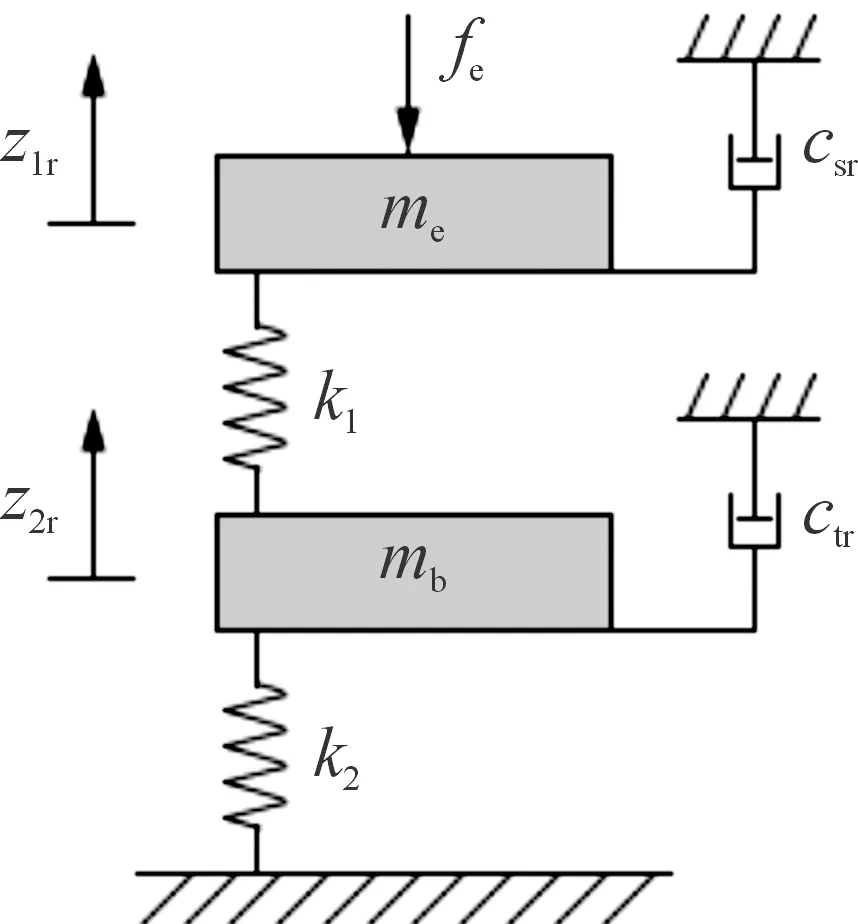
圖2 天棚阻尼參考模型
根據牛頓第二定律,得到天棚阻尼參考模型的動力學方程為
(4)
(5)
Xr=ArXr+BrW
(6)
其中,
W=[fe]
2 滑模控制器設計
基于天棚阻尼參考模型的滑模控制器設計的主要思路是:以理想天棚阻尼控制系統作為參考模型,在實際被控系統與參考模型系統之間建立誤差動力學模型,然后設計相應的切換函數和變結構控制律,使系統狀態軌跡在有限時間內到達所設計的切換面,實現系統滑動模態運動和漸近穩定性。
2.1 誤差動力學模型
根據建立的半主動懸置系統力學模型和天棚阻尼參考模型,定義發動機速度誤差、位移誤差和位移誤差的積分為廣義誤差矢量,即
(7)
(8)
由式(3)、式(6)和式(8)整理,得到誤差動力學方程為
(9)
其中,
2.2 滑模輸出阻尼力
滑模運動必須漸近穩定,并且所有控制點在進入滑模切換平面的過程中應具有良好的動態品質。實現對誤差矢量進行滑模變結構控制,通過建立的誤差動力學方程,采用極點配置方法設計的滑模面為
s=Ce
(10)
式中:s為滑模面;C=[1c1c2]為系數矩陣;e為狀態變量矩陣。則滑模面導數為
(11)
滑動模態的運動微分方程為
C(s)=c2+c1s+s2
(12)
式中:c1和c2采用極點配置方法求得。
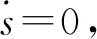
u=-(CGe)-1(CAee+CBeX+CHeXr)
(13)
根據式(3)、式(6)和式(13)整理可得
u=c2mek1(z1-z1r)+k1(z2-z2r)·
(14)
滑模控制的存在性和可達性條件為
(15)
在滿足式(15)的條件下,為改善滑模運動的品質問題,可采用等速趨近律
s=-φsgn(s),φ>0
(16)
其中,趨近律中的代表系統運動點趨近切換面的速率。選取合理的值可以加速趨近的過程,降低系統抖振。因此,得到的滑模控制器可控制阻尼力為
fc=u+φsgn(s)
(17)
對于半主動懸置系統,具有被動約束條件的可控阻尼力為
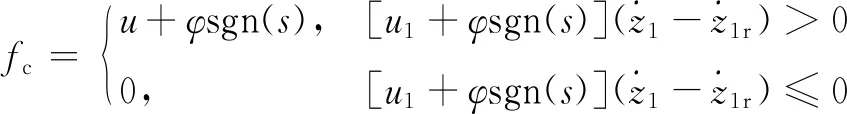
(18)
3 半主動懸置系統仿真模型
3.1 仿真模型建立
根據滑模控制理論,建立的基于天棚阻尼參考模型的半主動懸置系統滑模控制結構如圖3所示。
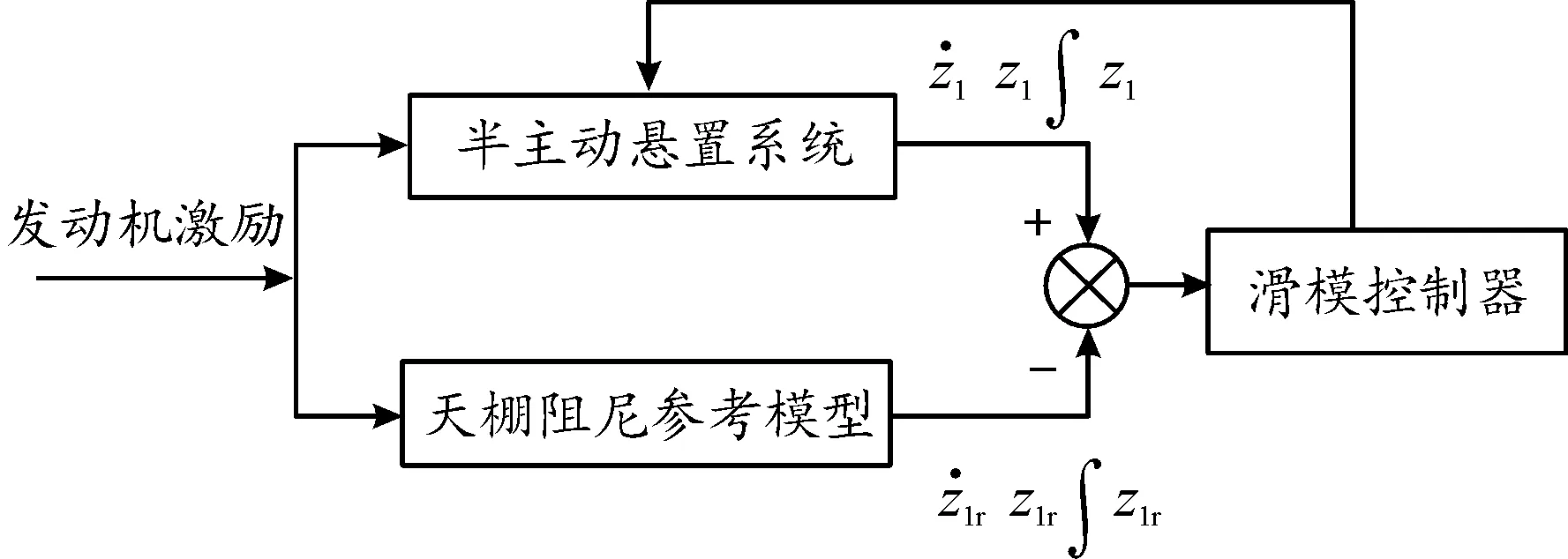
圖3 滑模控制結構示意圖
天棚阻尼參考模型是在理想固定端分別與發動機和車身之間添加天棚阻尼系數。天棚阻尼系數的選取對滑模控制器的控制性能有著非常重要的影響。以懸置系統二自由度力學模型為研究對象,在發動機激勵作用下計算出天棚阻尼參考模型中發動機加速度和懸置動撓度的峰值擬合曲線如圖4所示。天棚阻尼系數選取初始值為2 000 N·s/m、終止值為3 500 N·s/m、步長為250 N·s/m。由圖4可知,天棚阻尼系數小于3 000 N·s/m時,發動機加速度和懸置動撓度的峰值均隨天棚阻尼系數的增加而減小;而大于3 000 N·s/m時,發動機加速度和懸置動撓度的峰值變化不大。考慮發動機加速度和懸置動撓度峰值擬合曲線的變化規律,天棚阻尼系數ctr和csr均選擇為 3 000 N·s/m。
圖4 峰值擬合曲線
滑模控制是一種變結構控制,具有對外部的干擾不敏感性,適用于有擾動的非線性系統,具有良好的魯棒性。滑模控制存在抖振,對系統的切換控制項選取等速趨近律式(16),其中的切換系數對懸置系統的動態特性和抖振產生影響,可以通過試湊法,合理選擇控制參數為0.01,實現改善懸置系統的動態特性和降低抖振的目的。仿真模型參數值如表1所示。
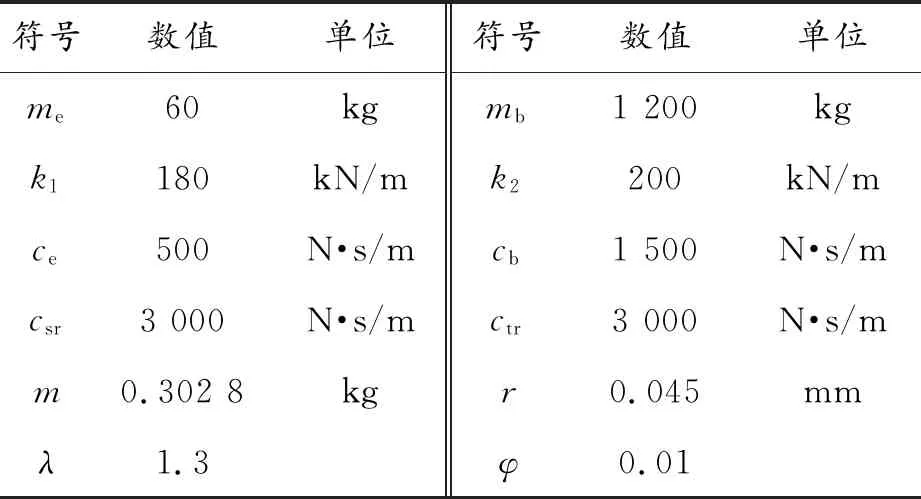
表1 仿真模型參數值
為了驗證基于天棚阻尼參考模型的滑模控制器的控制性能,在Matlab/Simulink平臺建立1/4半主動懸置系統仿真模型,如圖5所示。圖5中:fe為發動機激勵,fc為可控阻尼力,z1和z2分別為半主動懸置系統中發動機和車身位移,z1r和z2r分別為天棚阻尼參考模型中發動機和車身位移,ea為發動機加速度,mdd為懸置動撓度。
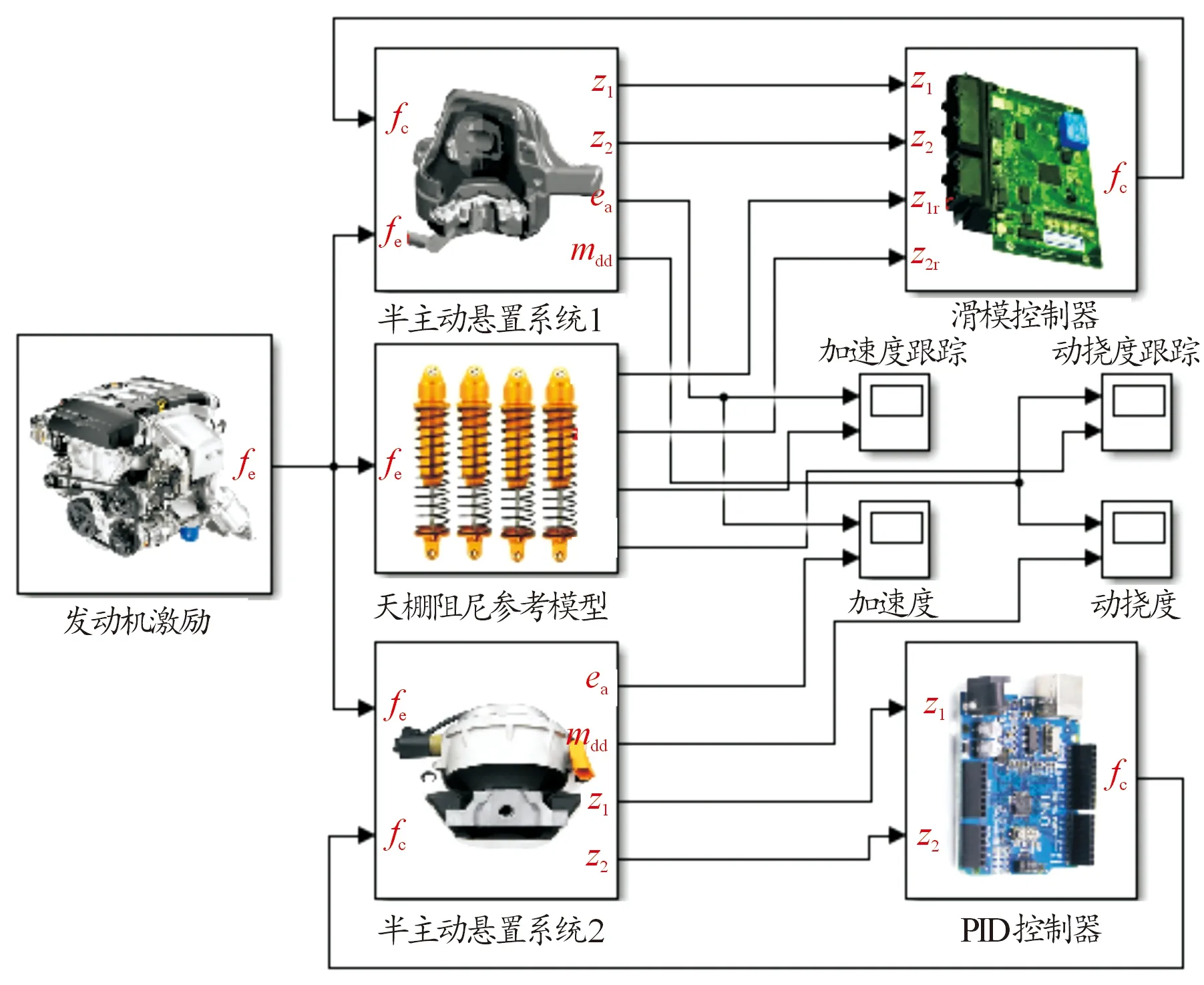
圖5 半主動懸置系統仿真模型
3.2 仿真結果分析
在發動機半主動懸置系統中,振動激勵分為內部激勵和外部激勵。內部激勵主要來自發動機,而外部激勵主要來自路面。由于懸架的減振作用,外部激勵對半主動懸置系統影響相對較小。內部激勵主要由發動機氣缸內的燃氣壓力和活塞往復運動產生的不平衡慣性力與扭矩等造成,然后通過懸置元件傳遞到車身,激勵著車輛不斷的產生振動。多缸發動機激勵一般可以等效為幾個單缸發動機激勵疊加而成。常用直列四缸發動機在垂直方向激勵為:
fe=-4mrλω2cos2ωt
(19)
式中:m為往復運動活塞的質量;r為曲柄回轉半徑;λ為曲柄回轉半徑與連桿長度的比值;ω為發動機曲柄角速度;t為時間。直列四缸發動機為偶數缸發動機,各缸的一階往復慣性力和旋轉慣性力因相互平衡而抵消。圖6為發動機在變工況下輸出的垂直方向激勵,(a)和(b)分別為汽車升降擋時發動機輸出的激勵,(c)和(d)分別為汽車加減速時發動機輸出的激勵。
基于天棚阻尼參考模型的滑模控制,需要適當調節半主動懸置輸出的可控阻尼力,使控制模型中的車身的運動特征和天棚阻尼參考模型中的等效質量運動特征一致。發動機加速度和懸置動撓度分別在滑模控制和天棚阻尼控制下的對比如圖7和圖8所示。由圖7和圖8可以看出,設計的滑模控制器具有很好的跟蹤效果,驗證了基于天棚阻尼參考模型的滑模控制在半主動懸置系統中的可靠性。
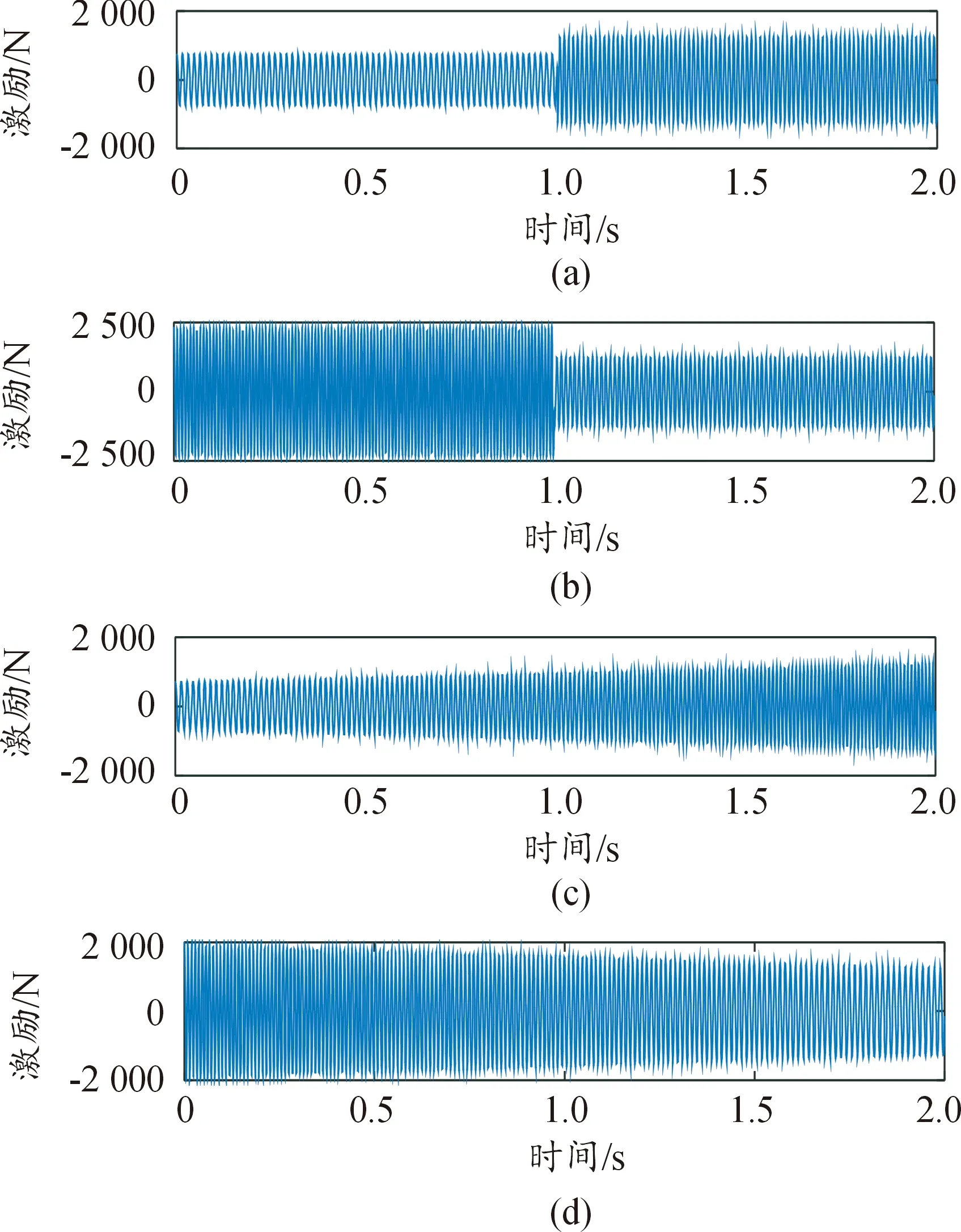
圖6 發動機變工況下激勵
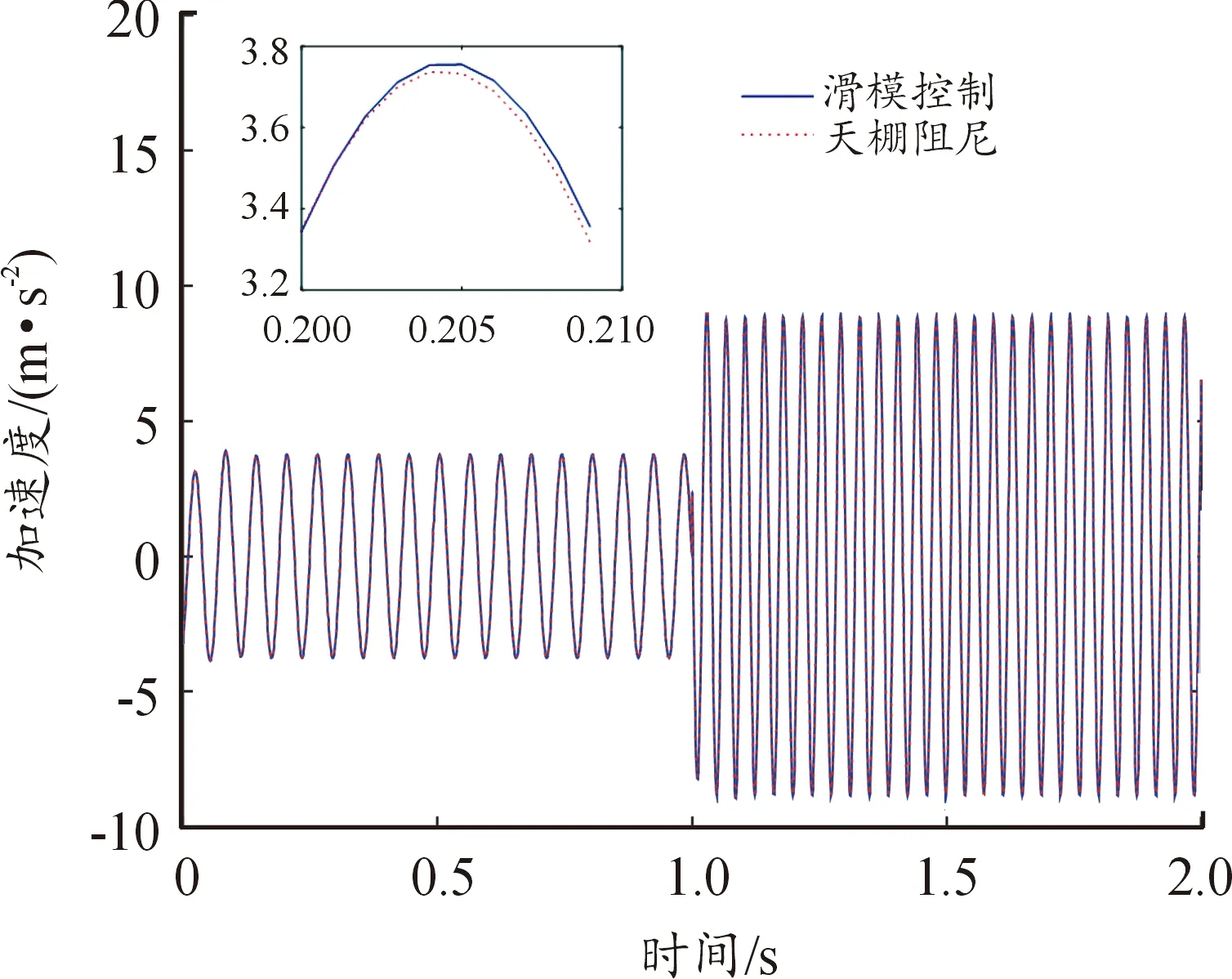
圖7 發動機加速度

圖8 懸置動撓度
汽車換擋時,發動機加速度和懸置動撓度分別在PID控制和基于天棚阻尼參考模型的滑模控制系統作用下的對比如圖9所示。由圖9(a)可知,發動機加速度峰值在減擋前為69.9 m/s2,采用滑模控制后為58.73 m/s2,降幅為15.98%,在減擋穩定后為34.82 m/s2,采用滑模控制后為20.24 m/s2,降幅為41.87%。由圖9(b)可知,懸置動撓度峰值在減擋前為0.249 5 mm,采用滑模控制后為0.237 3 mm,降幅為4.89%;在減擋后為0.246 3 mm,采用滑模控制后為0.187 8 mm,降幅為23.75%;懸置動撓度峰值采用PID控制時穩定時間為1.58 s,而采用滑模控制后為1.14 s。半主動懸置系統在采用基于天棚阻尼參考模型的滑模控制后,發動機加速度和懸置動撓度在不同擋位切換工況下能得到更好的抑制,系統趨于穩定的時間更短。
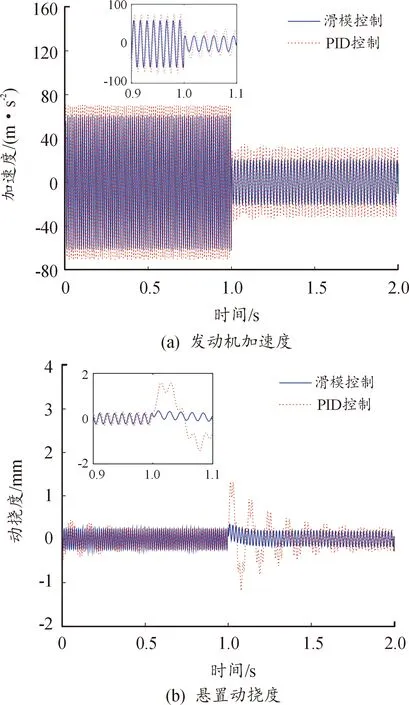
圖9 汽車升擋時系統動態特性
汽車改變車速時,發動機加速度和懸置動撓度分別在PID控制和基于天棚阻尼參考模型的滑模控制系統作用下的對比如圖10所示。由圖10(a)可知,發動機加速度峰值在車速100 km/h時為77.05 m/s2,采用滑模控制后為74.4 m/s2,降幅為3.44%;在車速80 km/h為48.08 m/s2,采用滑模控制后為29.78 m/s2,降幅為38.06%。由圖10(b)可知,懸置動撓度峰值在車速100 km/h時為0.291 3 mm,采用滑模控制后為0.251 1 mm,降幅為13.8%;在車速80 km/h為0.480 5 mm,采用滑模控制后為0.301 2 mm,降幅為37.32%。隨著車速的逐漸降低,滑模控制下的半主動懸置系統的減振性能逐漸上升,而懸置動撓度有所增加,這是因為車輛性能指標之間存在矛盾。半主動懸置系統在采用基于天棚阻尼參考模型的滑模控制后,發動機加速度和懸置動撓度在車速切換工況下能得到更好的抑制。
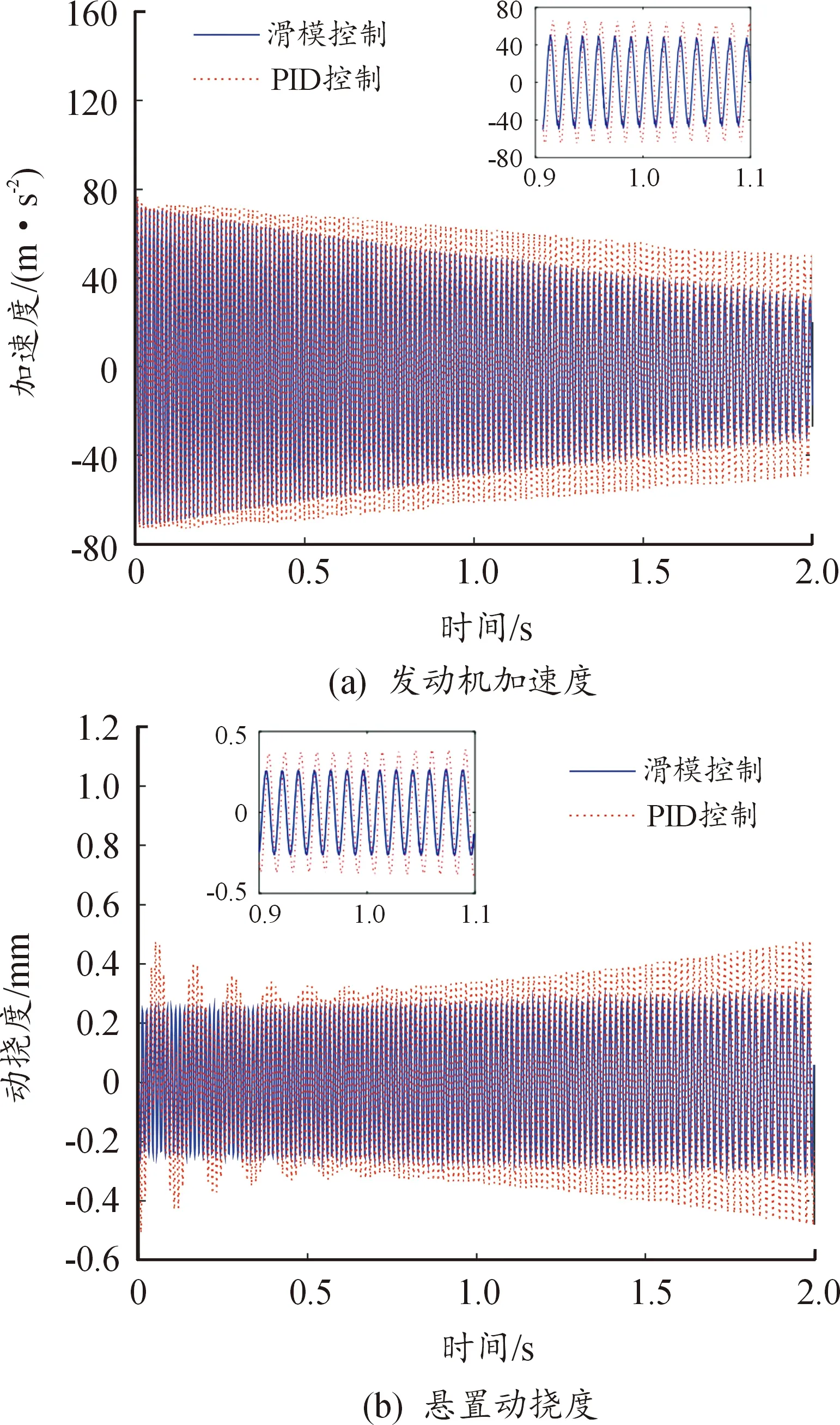
圖10 汽車減速時系統動態特性
為了深入探討變工況下滑模控制器的控制性能,結合表2中的各擋位車速與發動機轉速的對應關系[16],改變半主動懸置系統仿真模型的系統參數進行仿真研究。
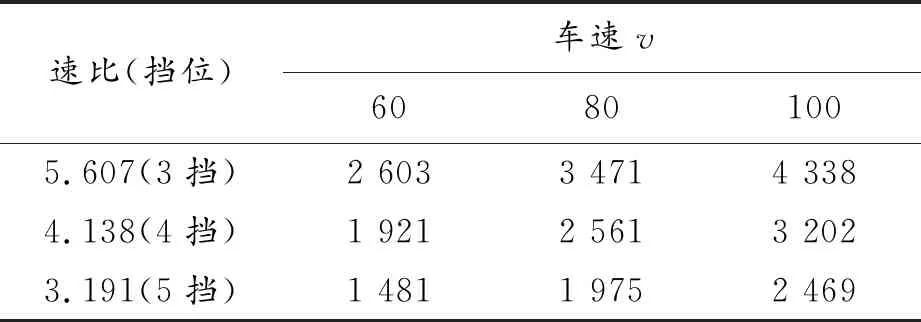
表2 各擋位車速與發動機轉速的對應關系 km/h
為了更直觀地反映半主動懸置系統在應用滑模控制器后隔振性能的改善程度,以發動機加速度的均方根值為其評價指標,其計算結果如表3和表4所示。
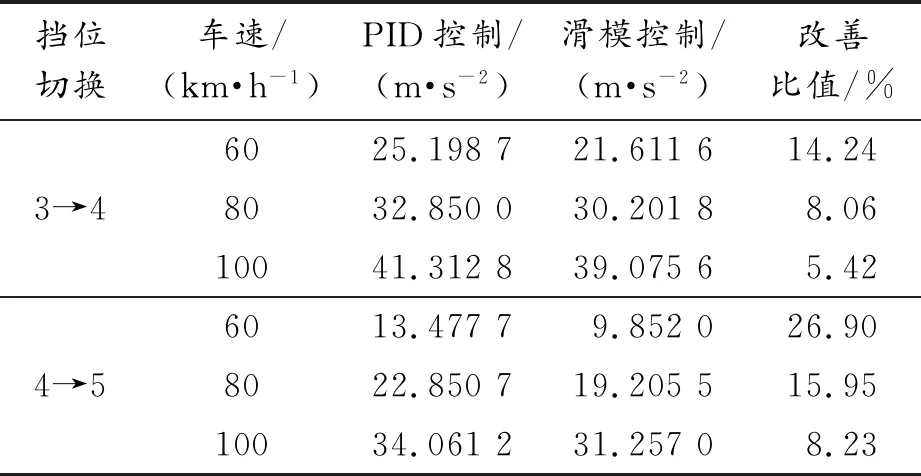
表3 擋位改變時滑模控制對發動機振動的影響
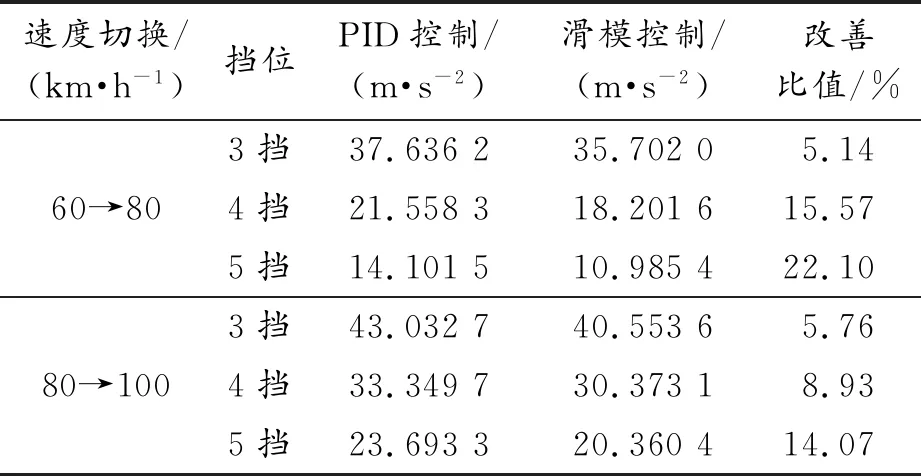
表4 車速改變時滑模控制對發動機振動的影響
由表3可知,擋位由3擋切換到4擋時,隨著車速上升,PID控制的發動機加速度由25.198 7 m/s2增加到41.312 8 m/s2,半主動懸置系統應用滑模控制后,發動機加速度由21.611 6 m/s2增加到39.075 6 m/s2,隔振性能改善比值由14.24%降低到5.42%。擋位由4擋切換到5擋時,隨著車速上升,PID控制的發動機加速度由13.477 7 m/s2增加到34.061 2 m/s2,半主動懸置系統應用滑模控制后,其發動機加速度由9.852 m/s2增加到31.257 m/s2,隔振性能改善比值由26.9%降低到8.23%。在相同擋位切換工況下,隨著車速上升,滑模控制改善半主動懸置系統隔振性能的效果隨之下降。
由表4可知,車速由60 km/h切換到80 km/h時,隨著擋位上升,PID控制的發動機加速度由37.636 2 m/s2下降到14.101 5 m/s2,半主動懸置系統應用滑模控制后,其發動機加速度由35.702 m/s2下降到10.985 4 m/s2,隔振性能改善比值由5.14%上升到22.1%。車速由80 km/h切換到100 km/h時,隨著擋位上升,PID控制的發動機加速度由43.032 7 m/s2下降到23.693 3 m/s2,半主動懸置系統應用滑模控制后,其發動機加速度由40.553 6 m/s2下降到20.360 4 m/s2,隔振性能改善比值由5.76%上升到14.07%。在相同車速切換工況下,隨著擋位上升,滑模控制改善半主動懸置系統隔振性能的效果隨之上升。
4 結論
為研究變工況條件下滑模控制對半主動懸置系統隔振性能的影響,設計一種基于天棚阻尼參考模型的滑模控制器,并在Matlab/Simulink平臺建立其仿真模型。仿真結果表明:設計的滑模控制器具有很好的跟蹤效果,驗證了基于天棚阻尼參考模型的滑模控制在半主動懸置系統中的可靠性;半主動懸置系統在采用基于天棚阻尼參考模型的滑模控制后,發動機加速度和懸置動撓度在擋位、車速切換工況下都能得到更好的抑制,系統趨于穩定的時間更短。為了深入探討變工況下滑模控制器的控制性能,結合各擋位車速與發動機轉速的對應關系,對半主動懸置系統隔振性能的改善程度進行了研究。分析結果表明:在相同的擋位切換工況下,隨著車速上升,滑模控制改善發動機半主動懸置系統隔振性能隨之下降;在相同的車速切換工況下,隨著擋位上升,滑模控制改善發動機半主動懸置系統隔振性能隨之提高。

