高中數學教材與課程標準的一致性分析

劉一冬　李逸蕓　楊作東

摘 要：通過SEC一致性分析方法，人教A版教材（2019年版）和蘇教版教材（2020年版）必修一“不等式”部分與2017年版課程標準總體上一致性顯著.在認知水平上，兩版教材與課程標準之間仍存在一定差異，在理解水平和探究水平的側重高于課程標準，在識記水平和應用水平的側重低于課程標準.建議教師整合題目資源，充分利用習題素材；建議教材編寫者重視高水平認知，及時更新習題配置.

關鍵詞：高中數學教材；課程標準；一致性分析

課程標準為課程實施提供指導方向，教材是數學課程實施的重要物化載體.美國研究者采用SEC一致性分析工具對數學教材與“課程標準”的一致性分析做了全面系統的調查實踐，經過了基礎測評（檢測一致性程度）、系統深化（檢測不一致程度）和模式改進（簡化分析模式）三個層次階段，研發了評估和改進基礎教育教科書質量的一致性分析模式［1］.目前我國中學數學的一致性研究總體上處于借鑒國外經驗的階段，主要集中在評價學業考試與課程標準的一致性，并有學者嘗試基于數學學科核心素養對一致性分析框架做本土化改進；也有少數學者對教師和學生認知的一致性進行了研究；而關于高中教材與課程標準的一致性研究相對較少.2017年我國教育部對高中數學課程標準進行了修訂，因此考查新課標思想理念在新教材中的落實程度以及如何考查顯得愈加重要.“不等式”在此次修訂中被調整為預備內容，筆者嘗試采用SEC一致性分析方法，就不等式內容對人教A版和蘇教版教材與《普通高中數學課程標準（2017年版）》（以下簡稱為課程標準）的一致性進行研究，并根據SEC模式的局限補充針對性分析.期望為評價課程實施和推動一致性模式本土化提供一定的參考，為教師教學和教材編寫提供一定的啟示.

1 研究方法與工具

一致性分析模式是指判斷、分析課程系統各個要素之間吻合程度的理念、程序與方法的總和［1］.Webb模式、SEC模式和Achieve模式是目前一致性分析的三大主流模式.SEC（Surveys of Enacted Curriculum——課程實施調查）模式由Porter，Smithson等人提出，本質上是一種內容分析法，相較于另外兩種模式，SEC一致性分析的靈活性與實用性較強，能夠對一致性進行整體性判斷，能夠廣泛應用于評價課堂教學、學業考試、教材與課程標準的一致性程度.在對教材的研究中，SEC一致性分析從內容主題和認知水平兩個維度入手，統計不同主題下不同認知水平的內容數，據此計算Porter一致性指數（Porter，2002）［3］，再根據臨界值（Gavin，2011）［4］來判斷一致性程度.為了提高編碼工作效率，提升一致性工具的可行性與使用性，Morgan等人對八種簡化方法進行比較，發現與教科書整體的一致性系數最為接近的三種簡化方法是“教科書的主要部分”“僅問題”和“每5個問題”［1］.由于例題習題也是我國教材的重要組成部分，本文采用“僅問題”的簡化方法，研究“不等式”例題習題與課程標準的一致性.

具體操作步驟如下：

（1） 構建內容主題×認知水平二維矩陣.確定內容主題和認知水平，分別劃分為t個主題和k個水平，并對其內涵進行界定.

（2） 編碼與統計.對課程標準的內容和教材的例題習題進行編碼，統計不同主題下不同認知水平的內容數，得到t×k頻數矩陣.

（3） 計算一致性系數.先對頻數矩陣進行標準化處理，再運用Porter一致性計算公式得到一致性系數P. Porter一致性公式如下：

其中aij和bij分別是課程標準和教材頻數矩陣標準化后的對應元素.

（4） 確定雙側臨界值，判斷一致性程度.首先將s項課程標準內容和r項教材內容（例題習題總數）分別隨機分配到t×k矩陣中，對兩個矩陣分別標準化處理得到P.將這個隨機模擬過程重復20000次，得到一致性系數分布.依據中心極限定理，P近似服從于正態分布.對其進行雙側檢驗（α=0.05）得到雙側臨界值，從而判斷（3）中所求一致性系數P是否在統計意義上顯著.若一致性系數小于下側臨界值，則認為不一致；若落在兩臨界值之間，則認為具有一致性，但一致性程度不顯著；若一致性系數大于上側臨界值，則認為一致性程度顯著.

本文利用MATLAB和SPSS軟件進行數據處理，對人教A版和蘇教版教材“不等式”例題與習題進行一致性分析.

2 研究過程

2.1 概念界定

不同學者對一致性涵義的解讀不同，但共同點在于描述一個系統中不同要素之間的匹配與吻合程度.本文將一致性界定為教材例題習題與課程標準的匹配程度.

2.2 維度劃分與編碼統計

首先確定內容主題.根據課程標準必修“不等式”部分的內容要求，內容主題維度劃分為“等式與不等式的性質”“基本不等式”“從函數觀點看一元二次方程”和“從函數觀點看一元二次不等式”四個部分（分別記為T1，T2，T3，T4）.

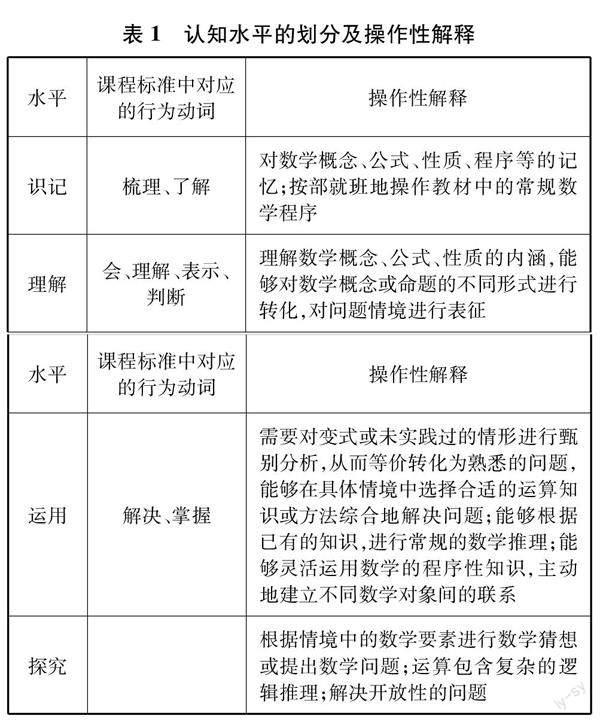
其次確定認知水平.我國課程標準中含有結果目標和過程目標，本文著眼于考查例題習題與課程標準的一致性，因此僅對課程標準中結果目標的認知層次進行劃分.參考青浦實驗以及李淑文等人的劃分對認知水平進行界定［5］，分為“識記”“理解”“應用”和“探究”四個層次（分別記為K1，K2，K3，K4）.

編碼以小題為單位，記錄其所屬的內容主題和認知水平.題目編碼舉例如下：

例1 計算下列兩個數的算數平均數與幾何平均數（其中p＞0）

（1） 2，8；（2） 3，12；（3） p，9p；（4） 2，2p2.

確定其內容主題，該題屬于“基本不等式”（T2）.確定其認知水平，該題目需要按照算數平均數和幾何平均數的定義計算即可.因此認知水平上屬于識記水平（K1）.

例2 已知不等式ax2+bx-1＞0的解集是{x|3＜x＜4}，求實數a，b的值.

確定其內容主題，該題屬于“從函數觀點看一元二次不等式”（K4）.確定其認知水平，解題需要聯系一元二次不等式、一元二次方程和二次函數之間的關系，得到a＞0，且3和4是對應一元二次方程的根，聯立方程可求得a，b.因此屬于理解水平（K2）.

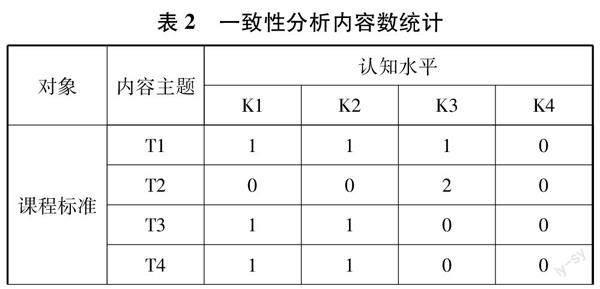
對課程標準和人教版、蘇教版兩版教材的內容數量進行統計，課程標準具體要求統計內容共9項，人教版教材統計內容共109項，蘇教版教材統計內容共164項.兩位碩士生各自獨立編碼，再對有分歧的題目進行討論.判斷編碼一致性，Cohens Kappa系數為0.718（p=0.000＜0.05），表明編碼一致性較強.取兩位編碼者的內容數統計的平均數作為統計結果.

3 兩版教材與課程標準一致性分析

3.1 總體情況分析

人教版教材例題習題與課程標準的一致性系數為0.6121，高于上側臨界值0.4407；蘇教版教材例題習題與課程標準的一致性系數為0.6081，高于上側臨界值0.4412.兩版教材“不等式”的例題習題與課程標準的一致性顯著.

3.2 局部情況分析

為了更直觀地呈現兩版教材“不等式”例題習題與課程標準的一致性情況，將教材數據統計矩陣（標準化后）與課程標準數據統計矩陣（標準化后）做差，并做出如圖1所示的等值線圖.

由上圖可知，兩版教材例題習題與課程標準發生偏離的分布大致相似，偏離以正偏離為主，在不同內容主題下對于認知水平的要求側重不同.

在內容主題維度，兩版教材的正偏離主要集中在“等式和不等式的性質”（T1）、“基本不等式”（T2）和“從函數觀點看一元二次不等式”（T4），負偏離主要集中在“從函數觀點看一元二次方程”（T3）.在人教版“不等式性質”部分，理解水平的題目占了不少比例，因此圖中（T1，K2）會出現較大的正偏離；兩版教材識記水平的題目幾乎沒有，因此（T1，K1）出現一定的負偏離.人教版“從函數觀點看一元二次方程”的例題和習題設置較少，因此T3會出現較大的負偏離；而蘇教版在這一方面更貼近課程標準.人教版和蘇教版對“從函數觀點看一元二次不等式”部分都設置了相當多的純計算題，因此兩版教材的T4都出現較大的正偏離.

在認知水平維度，兩版教材的正偏離主要集中在“理解水平”（K2）和“運用水平”（K3），其中正偏離較大的區域是（T2，K1）、（T2，K2）和（T4，K3）.此外，人教版的（T1，K2）和（T4，K1）也出現了較大的正偏離.人教版的較大負偏離主要集中在（T1，K1）、（T2，K3）和（T3，K2），蘇教版的較大負偏離重要集中在（T1，K1）、（T2，K3）和（T3，K1）.兩版教材對于“基本不等式”和“從函數觀點看一元二次方程”的認知側重不均衡.

為了具體地顯示兩版教材不等式例題習題在內容主題和認知水平上的差異，作權重柱狀圖如圖2所示.在內容主題上，兩版教材在“基本不等式”和“從函數觀點看一元二次不等式”部分的權重都高于課程標準，“從函數觀點看一元二次方程”的權重低

于課程標準，蘇教版教材在“不等式性質”部分的權重低于課程標準.在認知水平上，課程標準的要求在前三個水平較為均勻，未對“探究水平”作要求.而兩版教材在認知水平上的側重均是：理解＞運用＞識記＞探究.其中，人教版“運用水平”的權重低于課程標準，兩版教材“識記水平”的權重皆低于課程標準，但“理解水平”的權重皆高于課程標準，“探究水平”權重皆超出課程標準.

4 補充分析

SEC一致性分析方法在整體判斷上具有很大優勢，原有框架主要針對考查題目的認知水平，其他層面是否與課標相合，有待考查.另外，缺乏針對性的微觀分析也是SEC一致性模式的固有瑕疵［6］.下面筆者就題目的作答類型、情境類型，以及正文的引入展開作進一步探討.

筆者對作答類型進行統計，通過對例題習題的作答類型進行卡方檢驗，兩版教材不存在顯著性差異，說明作答類型結構相近.在新課標理念下、新高考導向下，開放性、探究性題目愈來愈成為命題趨勢，也將成為評價學生數學素養的有力工具.人教版設置了開放題和推廣題，蘇教版設置了閱讀題和猜想證明題，兩版教材都充分考慮了不等式一章的非常規型題目的設置，但它們的占比皆較少.對情境類型進行統計，兩版教材都設置了不同領域背景的題目，情境類型較為豐富，通過對例題習題的情境類型進行卡方檢驗，兩版教材不存在顯著差異，說明情境類型分布相近.通過情境化試題來評估學生的學業或素養已經成為國內外研究的共識［7］，復雜情境問題解決考查運用“整合的”邏輯、聯結知識點的能力，而非僅評估“量”的獲得.但是兩版教材中非純數學情境的題目占比相對較少，而以計算為主的“純數學情境”習題占據多數.

通過對兩版教材正文部分的引入與展開進行梳理，發現人教版教材采用的方式更為豐富，傾向于“問題情境”“圖表輔助”和“探究思考”，注重數學直觀，較多的運用類比、猜想等合情推理啟發學生思考知識之間的聯系，注重歸納思維的培養.蘇教版教材更多地采用“證明推導”，為學生展示了更多證明方法，更傾向于抽象、一般的陳述，更加注重培養演繹推理的思維品質和理性精神.根據喻平教授在《數學教學心理學》中提到的命題教學設計的三種模式［8］，對于“基本不等式”一節，人教版更傾向于發生型模式，蘇教版更傾向于發生型模式與問題解決模式相結合，兩者都十分注重命題的產生過程.

5 研究結論與啟示

5.1 研究結論

人教版和蘇教版教材不等式部分的例題習題與課程標準存在顯著的一致性.兩版教材與課程標準的偏離在內容主題和認知水平兩個維度上的分布大致相同，偏離以正偏離為主.從局部來看，兩版教材不等式的例題習題與課程標準仍有一定的出入，在理解水平和探究水平的側重高于課程標準，在識記水平和應用水平的側重低于課程標準.

5.2 研究啟示

課程標準和數學教材需要隨著社會經濟的發展、教育理念的進步而逐步優化.能夠從整體上對教材與課程標準的一致程度進行評估便是SEC一致性分析工具的價值所在，但一致性系數的高低并不能完全代表教材例題習題的水平，需要研究者辯證地分析看待.根據研究過程和研究結果，得到如下研究啟示.

5.2.1 認知水平界定與編碼主觀性影響研究結果

在研究過程中，需要在課程標準的結果目標認知水平和例題習題的認知水平之間找到一個界定的平衡點.但認知行為動詞實質上給出的是內部心理過程的劃分，難以嚴格判斷所屬認知水平.因此，一方面，編碼人員需要對課程標準和教材習題有深入的認識和理解；另一方面，研究者需根據研究內容對內容主題×認知水平的框架進行一定的改編.

5.2.2 整合題目資源，充分利用習題素材

研究結果發現兩版教材不等式例題習題與課程標準的一致性顯著，偏離以正偏離為主，體現了“下要保底，上不封頂”的課標落實理念.因此在實際教學中，教師應當首先把握課程標準，理解課程標準所提倡的多元要求，在此基礎上充分利用不同版本教材的習題素材，以最大程度地啟發學生的思維.另外，教師應當適當根據學生水平對習題進行改編和變式（比如蘇教版教材設置的解一元三次不等式的題目），以滿足不同層次學生的學習需求.

5.2.3 重視高水平認知，合理設置習題層次性

數學學科的六大核心素養都與高水平認知息息相關，而本文研究發現解一元二次不等式題目大量重復出現.筆者猜想這可能與“不等式”部分屬于“預備內容”以及“不等式”涉及數學運算的核心素養有關.但高水平認知要求的滲透是不可或缺的，數學運算包含了理解算理、運用邏輯推理、綜合解決問題等數學思維成分.建議教材編寫者及時更新習題配置，加大開發具有應用性、開放性和探究性題目的力度.在保證習題整體性的同時，重視習題的層次性和針對性，適當加大“運用水平”和“探究水平”題目的比重.讓學生更多地體會數學豐富的應用價值，認識數學深刻的思維品質，進而提升數學核心素養.

參考文獻：

［1］ 李秋實，劉學智.美國“課程實施調查”項目新進展：教科書與課程標準一致性分析模式研究［J］.外國教育研究，2019，46（7）：1528.

［2］ 劉學智，馬云鵬.美國“SEC”一致性分析范式的詮釋與啟示——基礎教育中評價與課程標準一致性的視角［J］.比較教育研究，2007（5）：6468.

［3］ Andrew C. Porter. Measuring the Content of Instruction： Uses in Research and Practice［J］. American Educational Research Association. 2002（7）： 314.

［4］ Gavin W. Fulmer. Estimating Critical Values for Strength of Alignment Among Curriculum， Assessments， and Instruction［J］. Journal of Educational and Behavioral Statistics，2011，36（3）： 381402.

［5］ 楊玉東，劉丹.教學目標測量的依據和工具——青浦實驗的新世紀行動之三［J］.上海教育科研，2007（10）：4346.

［6］ 段戴平.國外課程一致性研究范式述評及啟示［J］.高等理科教育，2016（6）：1419.

［7］ 王俊民，盧星辰，唐穎捷.國際大規模科學學業評估的試題情境比較研究——基于情境類型學的量化分析［J］.中國考試，2019（2）：3240.

［8］ 喻平.數學教學心理學［M］.北京：北京師范大學，2010：271273.

［9］ 武麗莎，朱立明，王久成.數學學科核心素養高考測評與課程標準一致性研究——以2019—2021年高考數學Ⅰ試卷為例［J］.數學教育學報，2022，31（3）：3944+83.

［10］ 朱立明.數學學科核心素養高考測評與課程標準一致分析框架的變證研究［J］.教育科學，2021，37（3）：5260.

［11］ 林釗，周瑩，路夢綺.不同版本教師用書與課程標準一致性分析——以蘇教版、北師版高中數學必修（教師用書）為例［J］.教學與管理，2019，769（12）：7477.

［12］ 龍正武，高存明，五旭剛.高中數學教材改革的創新與實踐［J］.課程.教材.教法，2020，40（7）：8691.

［13］ 徐小琴，張靜.人教A版高中數學教材若干問題的商榷［J］.教學與管理，2019，782（25）：3839.