突出建模過程　培養(yǎng)模型意識

洪靜

摘 要：在數(shù)學解題中發(fā)現(xiàn)，學生常因模型意識不強、對模型理解不深而出現(xiàn)“懂而不會”的情況.為了培養(yǎng)學生的模型意識，提高學生的建模能力，在教學中應帶領學生經(jīng)歷數(shù)學模型的“形成—建立—求解”的全過程，以此幫助學生認識數(shù)學的本質，提高學生解決實際問題的能力，提升學生數(shù)學素養(yǎng).

關鍵詞：模型意識；建模能力；數(shù)學素養(yǎng)

1 提出問題

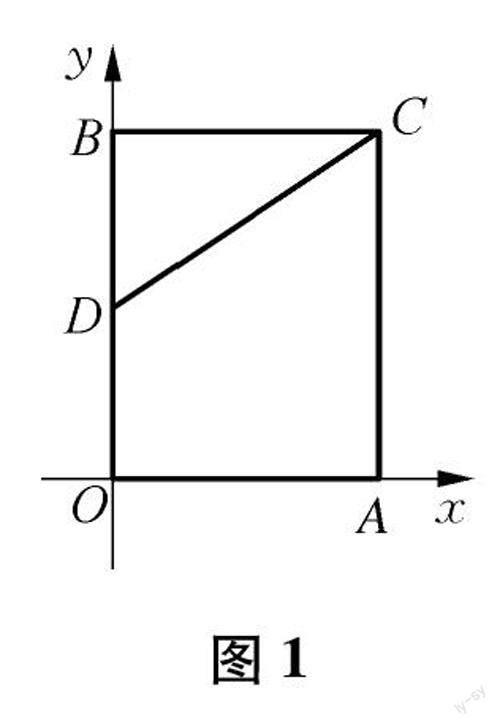
例1 如圖1，在平面直角坐標系xOy中，矩形OACB的頂點O在坐標原點，頂點A，B分別在x軸、y軸的正半軸上，OA=3，OB=4，D為邊OB的中點.

（1） 若E為邊OA邊上的動點，當△CDE的周長最小時，求點E的坐標；

（2） 若E、F為邊OA上的兩個動點，且EF=2，當四邊形CDEF的周長最小時，求點E、F的坐標.

例1為某校的模擬考試題，從得分上來看，問題（1）的正確率大約是60%，而問題（2）的正確率不到5%.問題（1）是一個典型的“將軍飲馬”的變式問題，此類問題在教學中重點講解并練習過，故得分率較高.而問題（2）其本質與問題（1）相同，但是因為問題的背景發(fā)生了變化，學生找不到原型可以模仿，為此正確率不高.

2 分析問題

那么造成問題（2）失分過高的根源到底是什么呢？通過調研發(fā)現(xiàn)，學生對于此類的“最短路徑”問題缺乏有效的方法，因此問題的背景略有變化，學生就表現(xiàn)得束手無策.

在實際教學中，受“講授式”教學模式的影響，學生對“兩點之間線段最短”這一模型并沒有理解透徹，所以在解題時未能通過有效的圖形變換構造“兩點之間線段最短”這一基本模型，故在解題時受阻.

3 改進策略

基于以上分析，為了幫助學生建構“兩點之間線段最短”這一基本模型，教師引導學生從不同背景“最短路徑問題”的解決中提煉出解決問題的通法，通過循序漸進的引導，幫助學生認識模型、理解模型、應用模型.在具體教學中，筆者以學生實際學情為出發(fā)點，通過專題教學引導學生運用圖形變換的觀點去審視圖形的構成，從而通過圖形的變換，將問題轉化為熟悉的模型，以此掌握模型的本質，提高學生應用模型解決問題的能力［1］.

3.1 明晰“兩點之間線段最短”模型

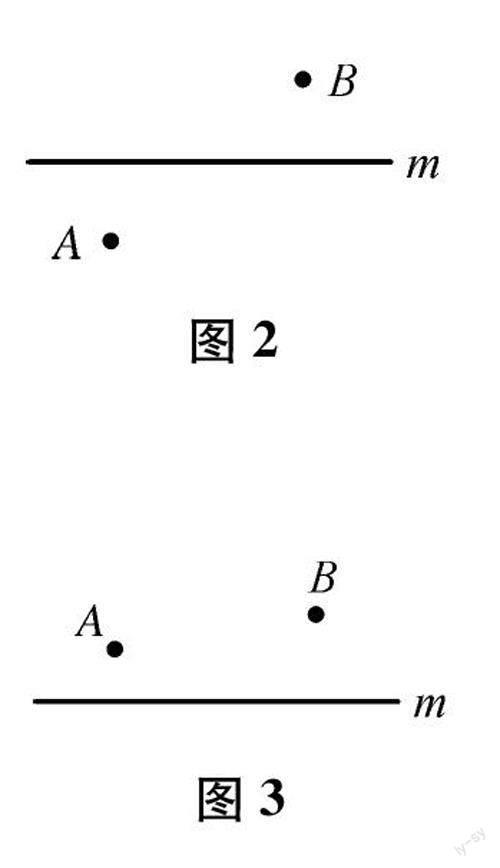
例2 如圖2，已知點A，B分別代表兩個村莊，直線m表示小河，現(xiàn)欲在河邊選一點P修個抽水站，向A，B兩個村莊修建水渠，問點P選在哪里可以使水渠的總長最短？

【設計意圖】讓學生明晰利用“兩點之間線段最短”這一基本模型是解決此類問題的基本方法，從而為接下來的問題解決做鋪墊.

3.2 利用軸對稱變換構造模型

例3 如圖3，已知點A，B分別代表兩個村莊，直線m表示小河，現(xiàn)欲在河邊選一點P修個抽水站，向A，B兩個村莊修建水渠，問點P選在哪里可以使水渠的總長最短？

問題1：請給出你的設計方案并說明理由；

問題2：根據(jù)例2，說一說為什么要用軸對稱的方法解決問題呢？

例4 如圖4，點A為某牧民家，他每天早上先要趕著牛羊去小河邊喝水（m表示小河），然后再將牛羊趕到草地吃草（n表示草地），請問他怎么走可以確保行駛的總路程最短？請畫出路線圖，并說明理由.

【設計意圖】在學習過程中發(fā)現(xiàn)，大多學生知道如何設計方案，但是卻不知道為什么這樣設計，可見學生在解決問題時還停留于簡單的模仿階段，并沒有認清問題的本質.基于此，在教學過程中，教師可以安排自主探究、互動交流等環(huán)節(jié)，從而通過交流掌握學生對這一模型的理解情況，以便教師通過有效地引導讓學生知道通過對稱軸來轉化的真正目的，從而讓學生真正理解、掌握并可以應用模型解決問題［2］.例3是這一教學模塊的核心，只有讓學生理解了、學會了，才能繼續(xù)后面模塊的探究，因此在此環(huán)節(jié)教師要給學生充足的時間進行互動交流，總結反思，確保每個學生都能真懂真會.例4實則例2的變形，是在原有基礎上的進一步拓展和延伸，其目的是通過巧妙的變化讓學生熟練掌握模型，并在變化中理解不變的數(shù)學模型.

3.3 利用平移變換構造模型

例5 如圖5，點A，B表示一條河兩邊的兩個村莊，現(xiàn)要在小河上修建一座垂直于河岸的橋CD，問橋CD修建在何處從B村到A村路程B-D-C-A最短？（假定河的兩岸是平行直線）

為了便于學生理解，在給出題目后，教師設計了如下問題鏈：

（1） 從B村到A村的路程由哪幾條線段組成？

（2） 決定路程長短的是哪些線段？

（3） 點D選在何處BD+CA的值最小？解決這個問題可以用軸對稱變換嗎？

（4） 你能用其他圖形變換將BD、CA轉化為首尾相接的形式嗎？

（5） 請給出你的詳解解題思路，并說明理由.

【設計意圖】借助問題鏈逐漸尋找解決問題的突破口.根據(jù)已知可知CD為定值，為此影響路徑長短的線段為BD、CA，因此問題就轉化為點D在何處使BD+CA取最小值.基于此，教師專門設計了問題（4），引導學生通過平移構造基本模型.從點D出發(fā)，每走1m，兩河岸就靠近1m，當從D走到C時，相當于兩河岸重合，這樣問題逐漸轉化為學生熟悉的模型.不過，根據(jù)平移的性質，此時B地也向河岸a平移了DC的距離到達點B′的位置.這樣問題可以轉化為：如圖6，在直線a上找一點C，使得AC+B′C最小.連接AB′交直線a與點C，過點C作CD⊥直線b于點D，則CD就是橋的位置.

3.4 利用旋轉變換構造模型

例6 如圖7，四邊形ABCD是正方形，△ABE是等邊三角形，M為對角線BD（不含B點）上任意一點，將BM繞點B逆時針旋轉60°得到BN，連接EN，AM，CM.

（1） 求證：△AMB≌△ENB；

（2） 當M點在何處時，AM+BM+CM的值最小？請說明理由.

問題（1）證明過程略，在解決問題（2）時需要思考這樣幾個問題：

問題1：若想AM+BM+CM的最小值，如何把AM、BM、CM這三條線段連接成一條線段呢？

問題2：根據(jù)△AMB≌△ENB，可以得到哪些有價值的信息呢？

（引導學生將AM轉化為EN）

問題3：由“將BM繞點B逆時針旋轉60°得到BN”這一條件能夠得到什么呢？

（連接MN，易證△BMN是等邊三角形，由此可以將BM轉化為線段MN）

【設計意圖】前面已經(jīng)學習了利用軸對稱變換和平移變換構造基本模型，在此基礎上引導學生進一步探究基本模型，通過旋轉來構造基本模型，以此通過不同變換解決同一問題（線段之和最短的問題），讓學生進一步領悟基本模型在解決問題的價值，深化對基本模型的理解.

3.5 利用多種變換構造模型

有了前面的探究和鋪墊，現(xiàn)在回歸至原始問題，即回歸例1.再次解題時，教師先讓學生獨立思考，嘗試通過圖形變換尋找解決問題的突破.從學生反饋來看，經(jīng)歷了前面的深層探究，現(xiàn)在已經(jīng)有一大半的學生可以獨立完成.不過因為本題第（2）問中涉及到兩種變換，即平移和翻折，所以對于一些基本較弱的學生來講仍具有一定的挑戰(zhàn)性，為此在此階段教師可以引導學生進行互動交流，通過分組討論的方式尋找有效的解題路徑.在互動交流中，教師了解了學生的實際困難，創(chuàng)設如下問題幫助學生突破難點：

問題1：在四邊形CDEF中，哪幾條線段定值呢？問題可以如何轉化呢？

問題2：問題（2）中線段DE和CF的位置與問題（1）中線段DE和CE的位置有何不同呢？

問題3：通過何種圖形變換可以將線段DE和CF的端點E和F重合呢？

【設計意圖】對比問題（1），引導學生通過觀察發(fā)現(xiàn)兩者的區(qū)別在于端點是否重合，由此引導學生通過平移變換構造基本模型，即將問題（2）逐漸轉化為問題（1），根據(jù)軸對稱變換順利解決問題.在解題時，既有教師的耐心引導，又有同學們的激烈爭論，讓學生進一步領悟數(shù)學的本質，深化對模型的理解.同時通過兩種圖形的變換，提高了學生分析和解決問題的能力.

4 教學反思

在初中數(shù)學教學中滲透模型思想能幫助學生認識數(shù)學的本質，提高學生解決實際問題的能力，對發(fā)展學生的思維能力等方面有著重要的價值.因此，在數(shù)學教學中，教師應帶領學生經(jīng)歷模型建構、模型深化的過程，并通過具體應用提高學生的模型意識，提高學生建模能力，以此提高學生數(shù)學綜合應用能力.

本節(jié)教學中，通過解題反饋發(fā)現(xiàn)問題（2）之所以得分低下，其主要原因就是學生沒有將“兩點之間線段最短”這一模型學懂、學透，這樣在解決簡單的問題時，學生可以通過模仿來解決，但是在面對復雜問題時就顯得束手無策.因此，為了幫助學生突破這一難關，教師借助具體案例引導學生清晰地認識模型，并通過圖形變換逐漸認清數(shù)學的本質，讓學生體會不同變換方法解決問題中的相同之處，從而在變中領悟不變的原理，激發(fā)學生學習熱情，提高學生數(shù)學素養(yǎng).

總之，在教學中，不要急于就題論題式的講解，要重視錯因的分析，善于通過循序漸進地引導讓學生將知識學懂學會.另外，在解題教學中，教師應重視模型思想的教學，突出建模過程，引導學生運用數(shù)學模型解決問題，以此提高學生解決實際問題的能力.

參考文獻：

［1］ 陳德前.培養(yǎng)學生模型思想的實踐與思考［J］.中學數(shù)學教學參考：中旬，2014（1）：124127.

［2］ 閆如明，呂吉華.對初中數(shù)學建模教學的幾點思考——以解直角三角形為例［J］.山東教育，2021（3）：5152.

［3］ 周靜君.課堂教學中培養(yǎng)學生主動會學策略探究［J］.數(shù)理化學習：教研版，2018（2）：2728.