兩道條件概率題的辨析*

廣州大學附屬中學 (510006) 朱驚濤

新人教A版教材使用以來,對條件概率的考查成為熱點,然而在一些地方命制的高三模擬試題中,出現了試題命制不嚴謹或者答案有誤的情況,分析這類題目,有助于增進我們對于條件概率問題的理解,試舉以下兩例進行分析:

例1 (2022年某市高三模擬題)高壓鈉燈使用時發出金白色光,具有發光率高、耗電少、壽命長、透霧能力強和不銹蝕等特點,廣泛應用于機場、碼頭、船塢、車站、廣場、街道交匯處等地方. 現在某公園中心樹立有一燈桿,桿上裝有6盞高壓鈉燈,每盞燈各使用燈泡一只,且型號相同. 假定每盞燈能否正常照明只與燈泡的壽命有關,該型號的燈泡壽命為1年以上的概率為p1,壽命為2年以上的概率為p2,從使用之日起每滿1年進行一次燈泡更換工作,只更換已壞的燈泡,平時不換.

(1)在第一次燈泡更換工作中,求①不需要更換燈泡的概率;②更換2只燈泡的概率;

(2)當p1=0.8,p2=0.3時,求在第二次燈泡更換工作中,至少需要更換5只燈泡的概率(結果保留兩個有效數字).

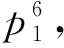
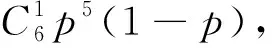
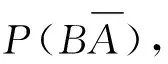
例2 (2022年某市高三模擬題) 某學校食堂開設一樓、二樓、三樓三個學生餐廳,A同學一天午餐隨機地選擇一個餐廳就餐．如果中午去一樓餐廳就餐,那么當天晚上不去一樓就餐的概率等于0.9;如果中午去二樓餐廳就餐,那么當晚去二樓就餐的概率等于0.7;如果中午去三樓餐廳就餐,那么當晚不去三樓就餐的概率等于0.8．還知道A同學晚上選擇在一樓與三樓就餐的概率相等．那么,A同學晚上選擇在一樓、二樓、三樓就餐的概率分別等于( ).

該題參考答案:

答案辨析:按題目條件給出的是“A同學晚上選擇在一樓與三樓就餐的概率相等”,應該解讀為P(B1)=P(B3),但是在該標準答案中,將這一條件理解為“P(B1|A2)=P(B3|A2)、P(B1|A3)=P(B3|A3)、P(B1|A1)=P(B3|A1)”,那么這兩者是否等價呢?答案是否定的.分析如下:

詳細可整理如下表:

P(B1A1)=0.1P(B2A1)=0.6P(B3A1)=0.3符合“中午去一樓,當天晚上不去一樓概率等于0.9”P(B1A2)=0.2P(B2A2)=0.7P(B3A2)=0.1符合“中午去二樓,當天晚上去二樓概率等于0.7”P(B1A3)=0.3P(B2A3)=0.5P(B3A3)=0.2符合“中午去三樓,當天晚上不去三樓概率等于0.8”