例析平移坐標系法求解函數問題

浙江省杭州第十四中學 (310006) 樓思遠

文[1]研究了平移坐標系法在圓錐曲線中的應用,實際上,平移坐標系法對處理部分函數問題也有立竿見影的效果.我們知道,在平面內對直角坐標系任意進行平移后,函數圖象的形狀、直線的斜率、線段的長度,多邊形的面積等均保持不變,特別的,只對直角坐標系左右平移時,函數的零點個數也保持不變,我們把這些不變的量統稱為“運動不變量”,基于這些不變量以及函數本身的性質,通過適當的平移坐標系來對解題思路作出調整,可起到化繁為簡的效果,并揭示出問題的本質.

一、實例分析

例1 若對任意的a,b∈R,不等式|x2+ax+b|≤1在區間[m,n]上恒成立,則n-m的最大值為________.

分析：原函數含有兩個參數,比較復雜,現將直角坐標系平移使得原點O與二次函數y=x2+ax+b的頂點重合,則二次函數解析式變為y=x2,如圖1所示,注意到平移過程中函數的形狀保持不變,因此可以將原問題轉化為在圖1的基礎上求解.

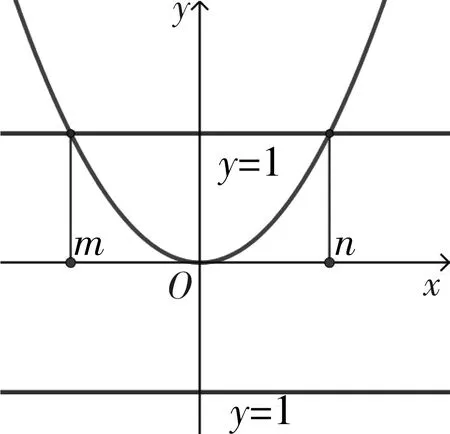
圖1

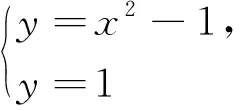
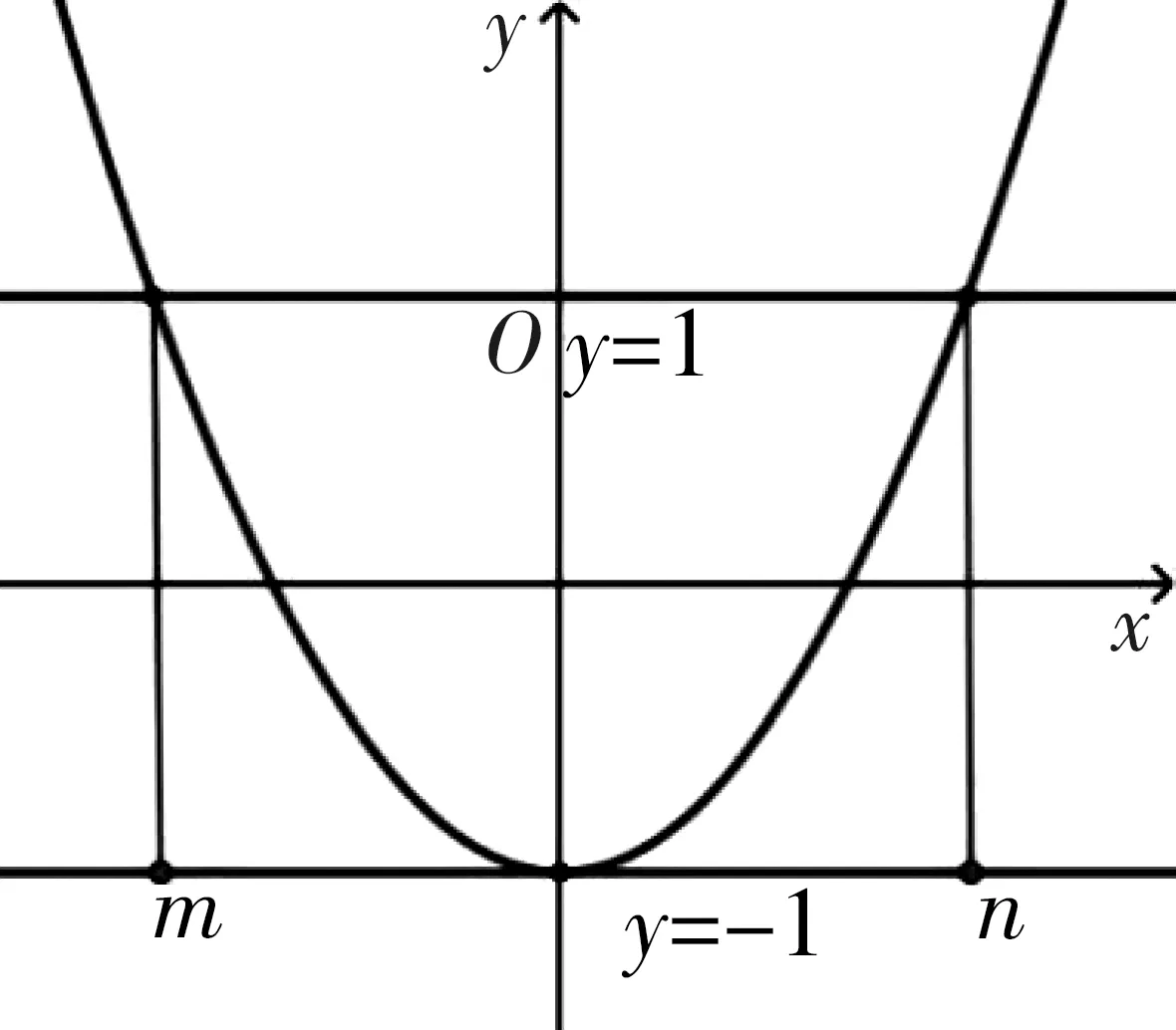
圖2

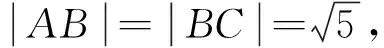
圖3

分析：在圖3中,函數過點(0,1),現將直角坐標系往上平移使得原點O與(0,1)重合,如圖4所示,此時函數解析式變為y=x3+x,是一個奇函數,由于平移過程中直線l的斜率與線段AB與BC的長度均保持不變,故根據對稱性知點B必然與原點O重合,在這種情況下,利用奇函數的性質可對問題快速求解.

圖4

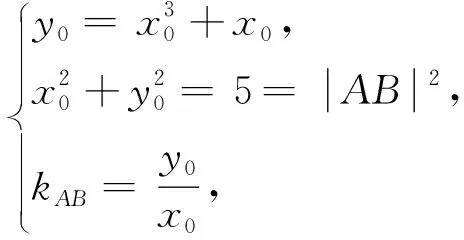
例3 如圖5所示,已知A,B,C,D為三次函數y=x3+ax2+bx+c圖象上不同的四點,A,C為兩個極值點且CD//AB,若A,B,C,D四點構成一個菱形,試求SABCD的值.

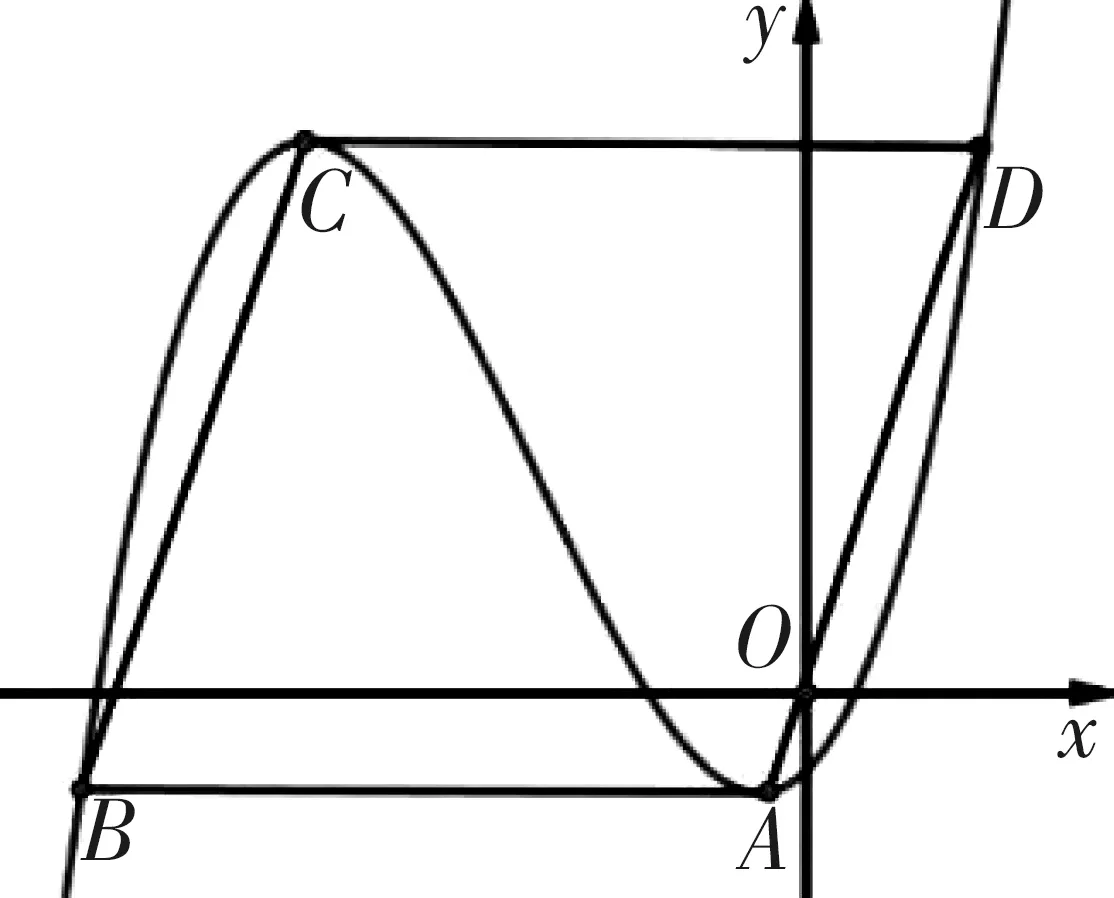
圖5

分析：原函數含有三個參數,比較復雜,現將直角坐標系平移使得原點O與點C重合,如圖6所示,根據零點位置可設三次函數解析式為y=(x-0)2(x-t),注意到平移過程中函數的形狀與SABCD面積大小均保持不變,因此可以在圖6情形下求解.

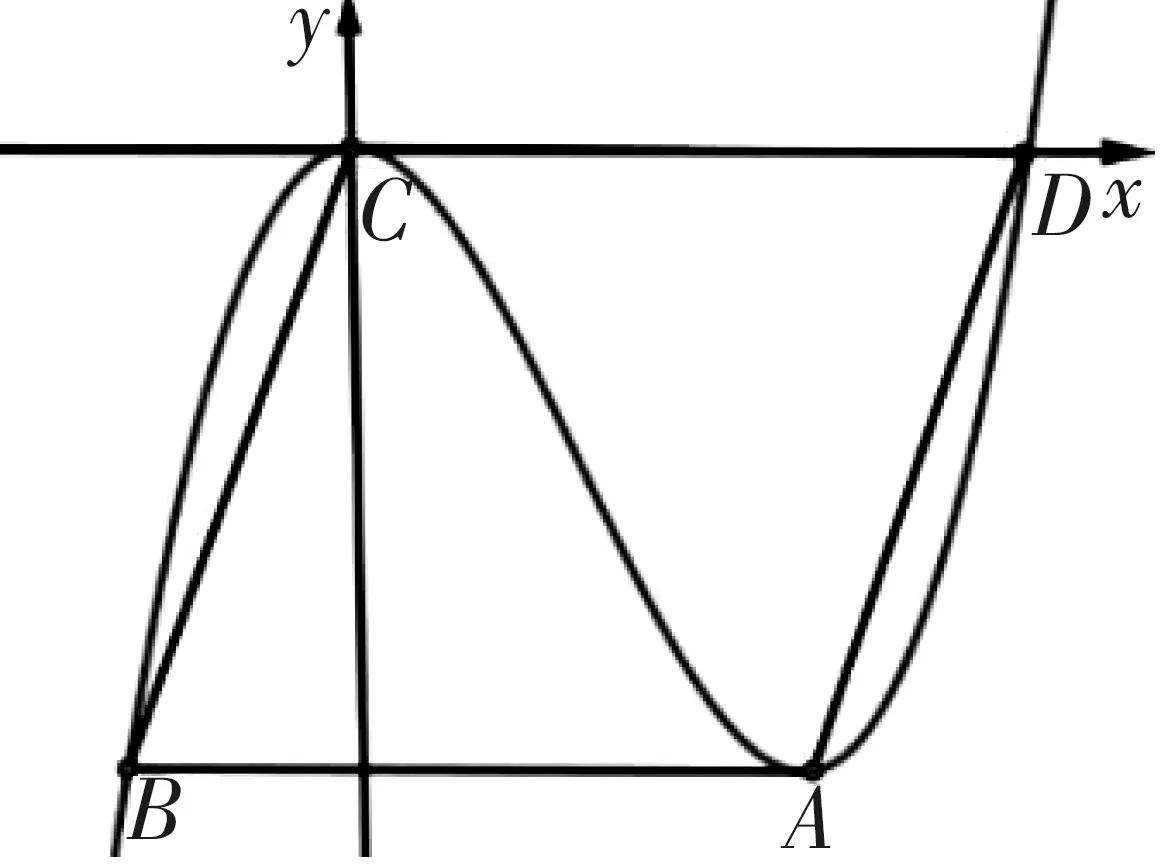
圖6

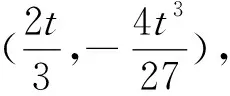
分析：將函數圖象左右平移不改變函數零點的個數,通過觀察和嘗試,發現將直角坐標系向右平移一個單位,可以使函數y=f(x-1)+f(1-x)變為y=f(x)+f(-x),為一個偶函數,根據對稱性,題目等價于y=f(x)+f(-x)=0當x>0時有兩個解.

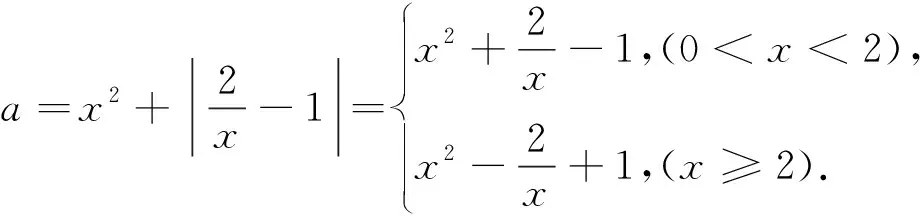
通過求導求得到函數的極值,并作出大致圖象如圖7所示,易知a>2時有兩個交點.故實數a的取值范圍是a>2.

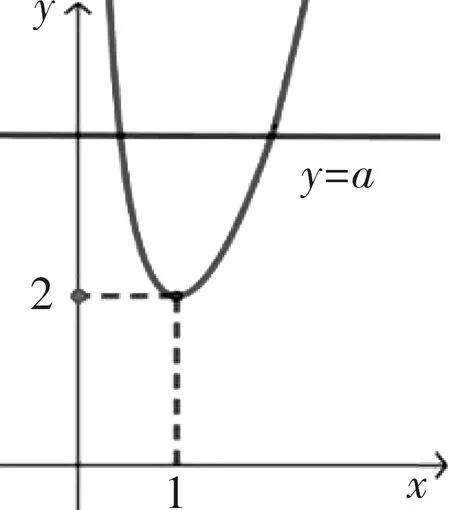
圖7

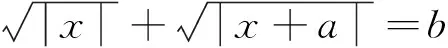
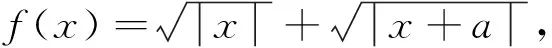
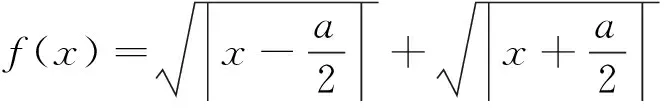
二．幾點思考

對上述幾個問題而言,直接求解將十分繁瑣,作為對照,通過平移坐標系這一操作,可以直指問題的本質,以簡馭繁快速解答.這其中,結合題意進行觀察與嘗試,發現并抽象出“運動不變量”是解題思路(平移直角坐標系)的關鍵,因此,數學抽象能力是根本所在.文[2]指出:“數學抽象是數學核心素養的重要構成內容,在新的教學改革中,數學抽象位于核心素養首位,意在通過對學生抽象素養的培養引導學生利用推理、運算、建模等數學活動方式揭示世界中蘊含的數學規律”.在平時的教學過程中,教師應重視學生抽象思維能力的培養,及時調整教學手段和教學方法,從情境與問題、知識與技能、思維與表達等維度開展數學抽象能力培養的教學,另外,可以引導學生結合直觀想象與數據分析等思維方式,從相似問題中抽象出一般性的數學規律與解題技巧.

本文僅就平面直角坐標系的平移展開了討論.實際上,從橫向角度而言,對空間直角坐標系進行平移,可以簡化立體幾何問題的坐標運算;從縱向角度而言,除了平移外,對直角坐標系進行旋轉與伸縮等變換,可以解決其各種類型的問題,例如通過旋轉坐標系可以將等軸雙曲線轉化為反比例函數的圖象,從而簡化運算過程,等等,此類問題待讀者進一步研究.