定積分視角例析幾道不等式問題的證明
2023-07-19 02:43:52廣東省深圳市鹽田高級中學518081陳一君
中學數學研究(江西) 2023年8期
關鍵詞:性質
廣東省深圳市鹽田高級中學 (518081) 陳一君
眾所周知,定積分有其直觀明了的幾何意義以及簡明性質.在教學中發現,以定積分的視角,借助定積分的幾何意義與相關性質來審視某些不等式的證明,可以得到這些不等式簡潔明快的證明過程,且具別開生面之感.本文對一些不等式通過定積分視角予以證明,以供教學參考.
例1 若a,b>1,證明ea-1+blnb≥ab.
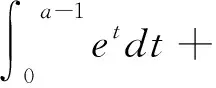

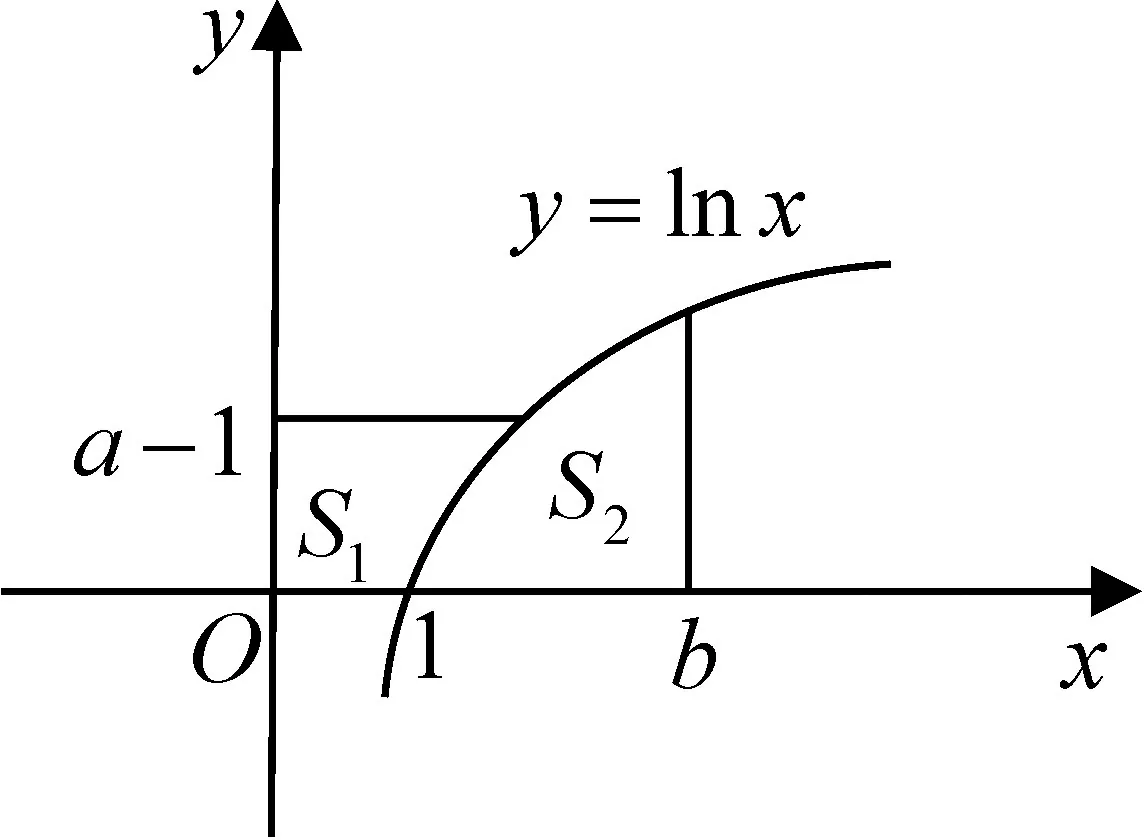
圖1
評析:上述證法的關鍵在于,以定積分視角審視不等式,揭示不等式結構中隱含的定積分元素,從而借助直觀的面積不等關系證得不等式.
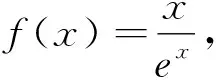
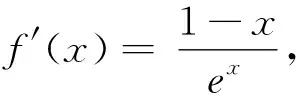
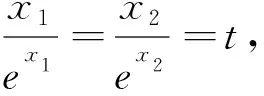
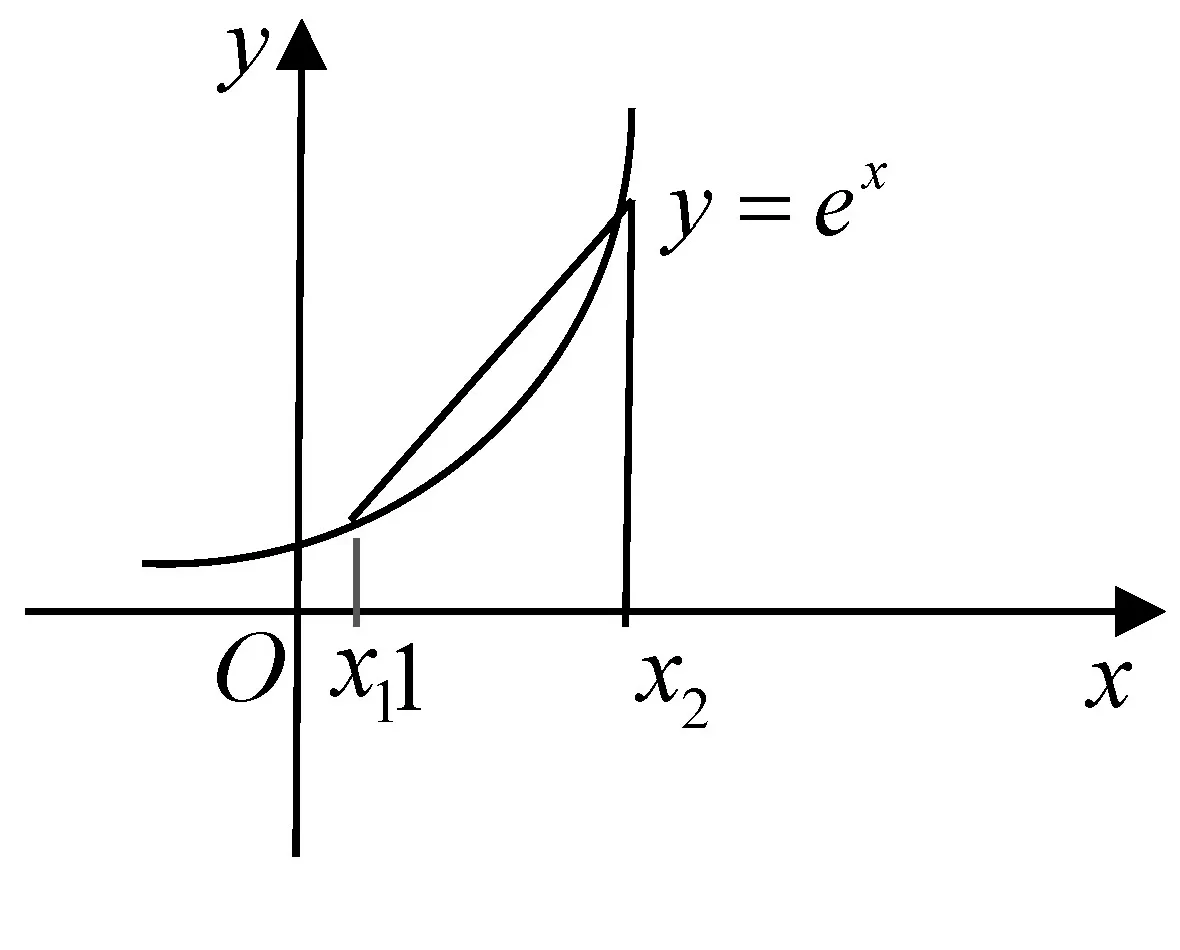
圖2
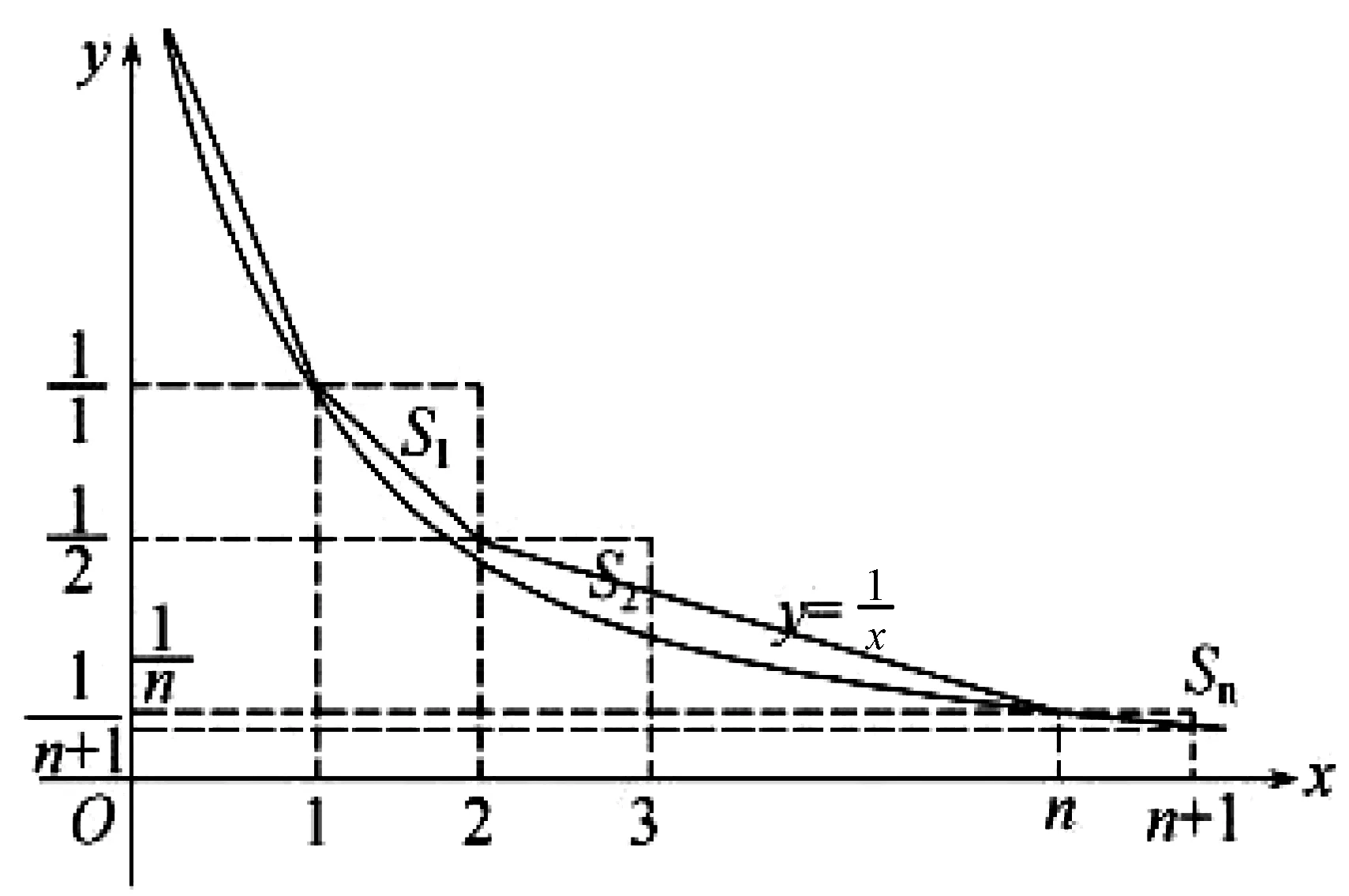
評析:上述證法,首先需要借助導數,明確f(x)單調性,從而得到隱含條件0 圖3 評析:上述證明的關鍵在于從定積分視角,仔細審視不等式結構,由圖形中析取蘊含其中的不等關系. 評析:上述證明的關鍵是通過兩種不同情形,得到不等式后,利用定積分性質,得到其證法. 評析:本例是熟知的對數均值不等式,其證明依托定積分性質,給人耳目一新之感. 簡析:(1)因為f(0)=1-a<0,f(2)=e2-2-a≥e2-4>0,所以y=f(x)在(0,+∞)上存在零點.因為f′(x)=ex-1,所以當x>0時,f′(x)>0,故函數f(x)在[0,+∞)上單調遞增,所以函數以y=f(x)在(0,+∞)上有唯一零點. 圖4 評析:本題為浙江省2020年的高考壓軸題,上述證明是基于定積分性質給出的,顯見其證明更簡便快捷.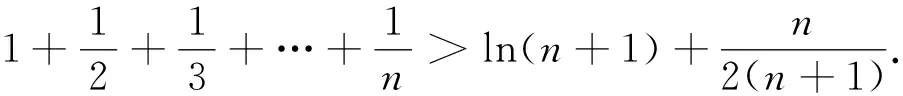
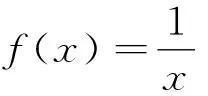
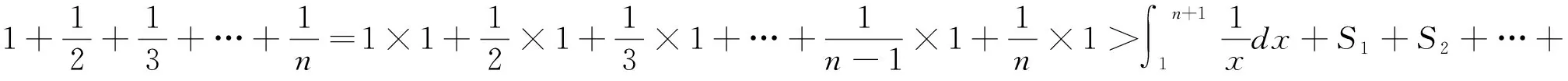
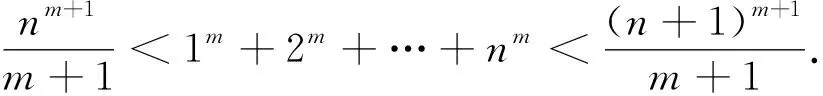
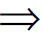
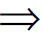
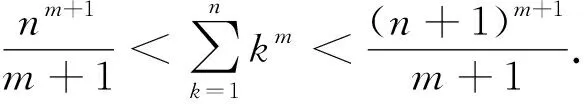
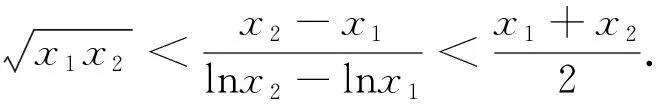
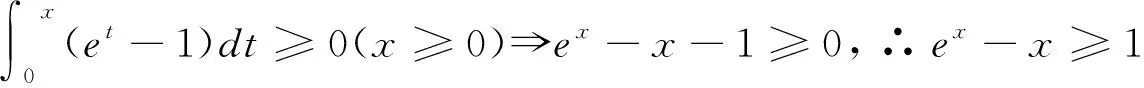

猜你喜歡
中學生數理化·高三版(2023年6期)2023-07-19 11:17:53
數學物理學報(2022年6期)2022-12-15 08:45:02
上海師范大學學報·自然科學版(2022年3期)2022-07-11 03:05:59
數學雜志(2021年6期)2021-11-24 11:12:00
中學生數理化(高中版.高二數學)(2021年5期)2021-07-21 02:14:46
數學年刊A輯(中文版)(2021年1期)2021-06-09 09:31:56
中等數學(2020年6期)2020-09-21 09:32:38
山東農業工程學院學報(2019年11期)2020-01-19 02:49:10
數學物理學報(2019年6期)2020-01-13 06:07:52
中等數學(2019年6期)2019-08-30 03:41:46

