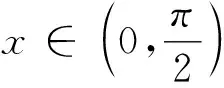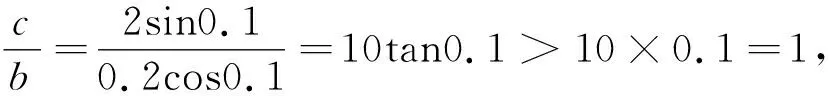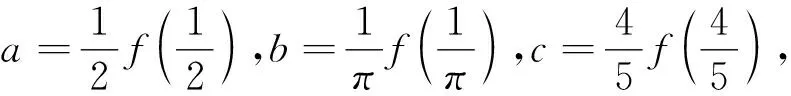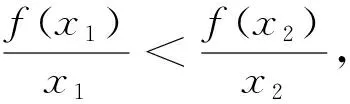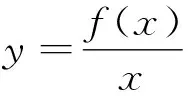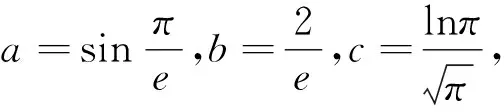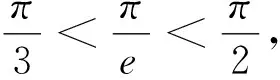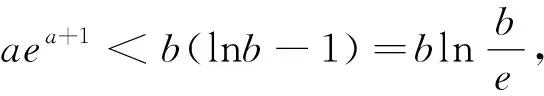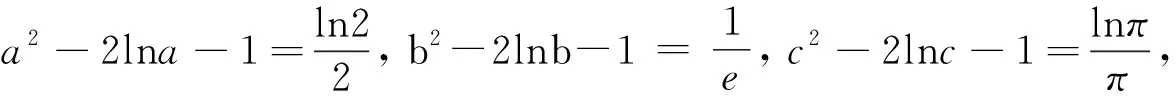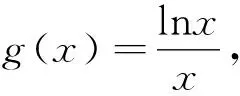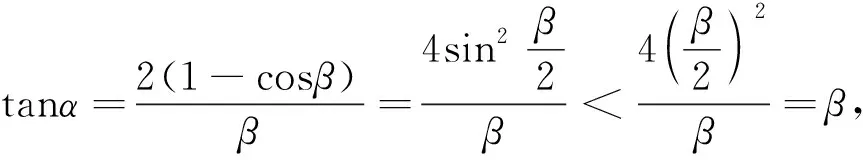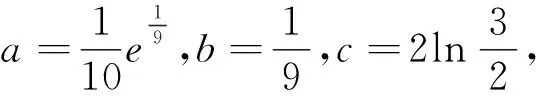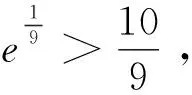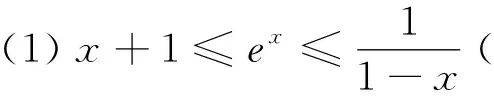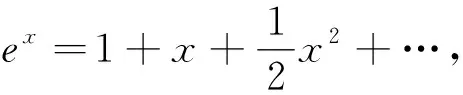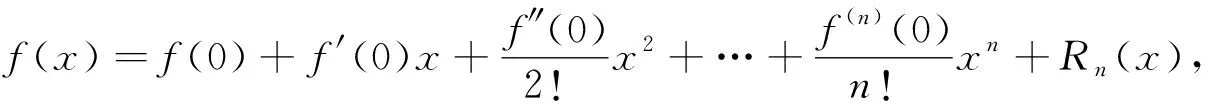觀察結構特征 思悟內在本質
——以破解比較大小問題為例

江蘇省西亭高級中學 (226300) 瞿春波

江蘇省南通市通州區教師發展中心 (226300) 瞿國華

從2023年2月的四省聯考到各地模考,甚至近幾年的高考中,時常在小題中看到比較大小的“影子”,它往往將冪(指數及對數)函數和三角函數、導數等聯系在一起,這類問題交匯性強,難度較大.本文通過實例總結破解該問題的幾種優化方法,供參考.

例1 (2023屆四省2月聯考)已知a,b,c滿足a=log5(2b+3b),c=log3(5b-2b),則( ).

A．|a-c|≥|b-c|,|a-b|≥|b-c|

B. |a-c|≥|b-c|,|a-b|≤|b-c|

C. |a-c|≤|b-c|,|a-b|≥|b-c|

D. |a-c|≤|b-c|,|a-b|≤|b-c|

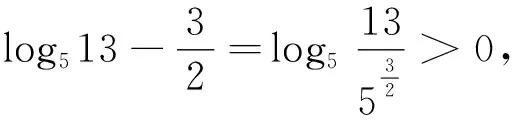
點評：由b的范圍,從特殊情況入手,得a,b,c大小關系,再用二分法精確a,c的大致范圍,從而去掉絕對值比大小.另外,用數形結合、極限、構造函數等方法也能破解此題.

例2 (2023屆齊魯名校高三二聯)設a=sin0.2,b=0.2cos0.1,c=2sin0.1,則( ).

A.a

C．b

點評：作商后,三角化簡,再利用三角函數線放縮為冪函數的值,從而比較大小.

A.a

C.b

A.a>b>cB.b>c>a

C.c>a>bD.b>a>c

例5 (2020屆濟南高三二模)已知實數x,y,z滿足z·lnx=z·ey=1.則下列關系式中不成立的是( ).

A.x>y>zB.x>z>y

C.z>x>yD.z>y>x

點評：通過構造關于k(k>0)的三個函數,結合圖象,比較函數值x,y,z的大小.

例6 (2022屆T8高三一聯)設a,b都為正數,aea+1+b

A．ab>eB.b>ea+1C．ab

點評：對條件變形,觀察結構特征,構造函數f(x)=xlnx并確定單調性,從而得到自變量值的大小關系.

A．b>a>cB．b>c>a

C．a>b>cD．c>a>b

點評：通過兩次構造函數,先比較g(x)函數值大小,再比較f(x)自變量值大小.

A.a

C.c

例10 (2023屆綿陽高三二診理科卷)設x=e0.03,y=1.032,z=ln(e0.6+e0.4),則( ).

A.z>y>xB.y>x>z

C.x>z>yD.z>x>y

總之,比較大小問題,形式多樣,方法靈活,但離不開基本知識和方法,掌握此類問題的通性通法,熟練變形技巧與破解策略,從而讓數學核心素養落地生根.