例談利用齊次化求一類分式遞歸數列的通項

山西省太原市第三實驗中學校 (030031) 董立偉

人教A版《普通高中教科書數學選擇性必修第二冊》(2020年5月第1版)(以下簡稱“選修二”)第四章《數列》部分出現了許多由一次分式形式的遞推關系猜想通項公式的數列問題. 這類問題本身并不難解,但學生們更想知道的是如何通過嚴格的推理得到這類數列的通項公式. 對分式遞歸數列,我們熟知的求通項的解法是不動點法. 這種方法確實巧妙,但是學生們也只能套用,很難理解其深刻的數學內涵. 事實上,利用齊次化的方法可以得到求解此類數列通項公式的一種初等解法.

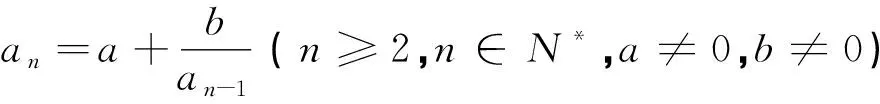
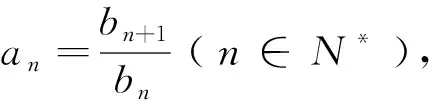
第三步(構造).利用待定系數法構造新的等差或等比數列求數列{bn}的通項公式;

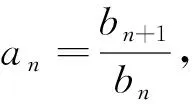
以下用兩個例子來闡述該類型問題的解法.

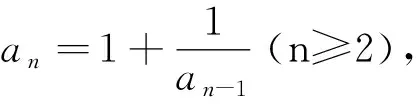
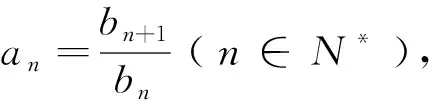
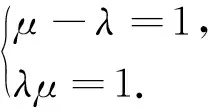
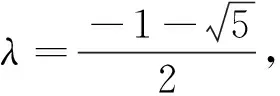
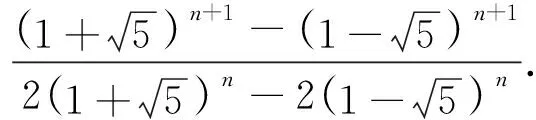
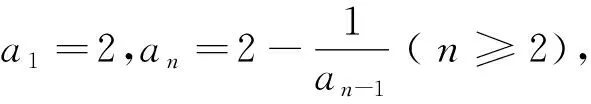
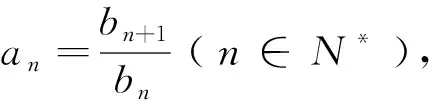
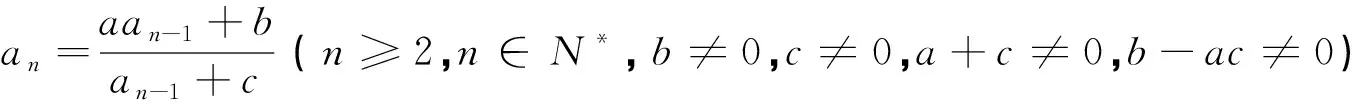
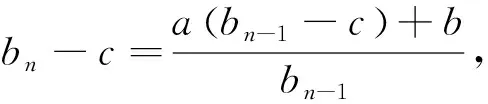
以下用兩個例子描述該類型問題求解過程.

例3 (選修二第48頁例3改編)已知數列{an}滿足a1=0,2an+1-anan+1=1(n∈N*),求數列{an}的通項公式.

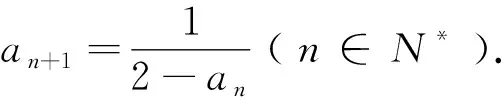
例4 (選修二第51頁習題4.4第3題改編)已知數列{an}滿足a1=1,4an+1-anan+1+2an=9(n∈N*),求數列{an}的通項公式.

結語：利用齊次化,我們將一次分式形式的遞推關系轉化為二階線性遞推關系,進而可以利用待定系數法構造新的等差或等比數列,求得其通項公式,從而得到此類問題的一種更易為高中生接受的初等解法.