泵站空管啟動充水過渡過程的波追蹤計算方法

曾宗耀，陰鑫月，秦 豪，王玉川，楊建國

（1. 西北農林科技大學，陜西 楊凌 712100； 2. 渭南市東雷抽黃工程管理中心，陜西 合陽 715300）

0 引 言

空管啟動充水過程是泵站輸水系統和管網中重要的水力過渡過程之一，期間易出現電動機過載和管道壓力波動等危害泵站安全穩定運行的現象［1-3］。計算分析泵站空管啟動充水過渡過程可以指導工作閥門的開啟規律和管路防護措施的布置［4，5］。

泵站空管啟動充水過程作為有壓管道充水過程，目前的水力過渡過程計算模型有剛性水柱模型和彈性水柱模型［6］。彈性水柱模型是基于特征線法和界面追蹤法相結合的模型，即假設在整個充水過程中水氣交界面與管軸線垂直，在水柱長度不斷變化的過程中追蹤水氣交界面的位置，其中交界面一側的有壓流采用特征線法求解，另一側的氣體流按照慣性氣體的狀態方程求解［7，8］。相比較而言，剛性水柱模型計算效率高但計算精度較低，而彈性水柱模型雖然計算精度高，但特征線網格內部節點的求解增加了計算量。

雖然特征線法與界面追蹤法可以模擬泵站輸水管路空管啟動充水的水力過渡過程，但特征線網格的特點決定了特征線法難以實現節點之間水氣交界面邊界條件的準確描述。波追蹤法的理論基礎與特征線法一致，但通過對空間量x而非時間量t的微分與轉化，使得過渡過程計算的物理意義更加明確、計算量更小，且能更精確地對交界面進行追蹤［9］。計算結果和實驗結果對比發現［10］，波追蹤法在計算精度和計算效率的博弈中顯得更為靈活，基于其建立的計算模型分類介于剛性模型與彈性模型之間。

利用波追蹤法與界面追蹤法建立了泵站空管啟動充水過渡過程計算的剛性模型和彈性模型；計算了某泵站空管啟動充水的水力過渡過程特性，通過對比計算結果與實驗結果驗證了計算模型的可靠性。研究對泵站空管啟動充水過程水泵工作參數和水錘波的變化規律及其計算提供了理論指導。

1 數學模型

1.1 泵閥模型

泵站輸水系統示意圖如圖1 所示，由于進水池-水泵-閥門之間的管道較短，且進水池水位變化很小，故忽略進水管道的影響，將進水池視為水泵進口處的恒壓邊界。同時，為了簡化水泵和泵后閥門之間的關系，把兩者當成一個整體作為統一的邊界。

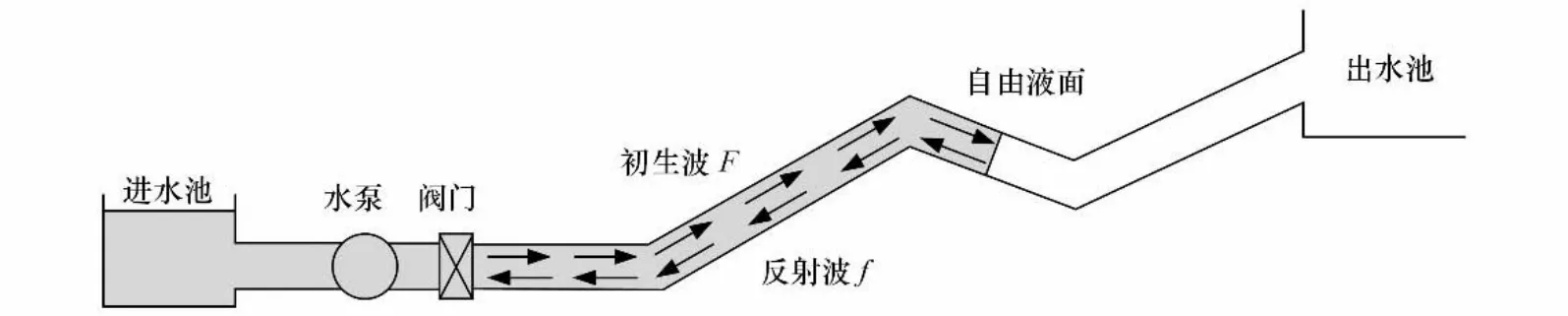
圖1 泵站輸水系統示意圖Fig.1 Water conveyance system of pump station

閥門流量與壓降關系有：

式中：Q為通過閥門的流量；hr為水泵吸水側水頭，即進水池水位；Δhpu為水泵揚程；hv為閥后水頭；τ為閥門相對開度；Cv為閥門全開水頭損失系數。

在泵站空管啟動充水過程中，閥門動作將在閥處產生升壓波向出水池方向傳播，同時受到充水水柱自由液面處反射回來的降壓波影響，故閥后水頭、流量及降壓波的關系有：

式中：f為反射返回閥門處的降壓波；hv為閥后水頭；hv0為閥后初始狀態的水頭；a為水錘波波速；g為重力加速度；A為閥后管道面積；Q為通過閥門的流量；Q0為閥后初始狀態的流量。

由于在空管啟動充水過程中，泵后閥門在水泵轉速達到額定轉速后才開啟，故泵閥模型可以分為兩階段，第一階段，水泵啟動，泵后閥門不開啟；第二階段，水泵保持額定轉速轉動，閥門按啟動規律動作。對于第一階段，閥后輸水管道并未充水、流量為零，而在水泵處，隨著水泵轉速持續增加，水泵揚程亦持續增大，可由全特性曲線插值計算得到。第二階段，泵閥作為一個典型的邊界，此時水泵轉速保持額定轉速，故聯立方程（1）、（2）并對水泵全特性曲線中額定轉速下的Q-Δhpu曲線進行插值，即可求得泵閥模型的Q、Δhpu與hv。

1.2 彈性模型

為了確定泵站空管啟動充水過程中輸水管道內水氣交界面的位置，假設水氣交界面垂直于管軸線，這是因為水氣交界面在整個充水水柱中所占比例較小，水氣交界面的形態對充水瞬變流的整體影響并不十分明顯。

如圖1 所示，對于t時刻已充滿的管道，可建立波追蹤方程［11］：

式中：F（x-a t）為管道任一點x處的初生波；F（x0-a（t-x/a））為Δt1時間間隔前閥門處產生的初生波，Δt1=x/a；Rx為衰減系數，Rx=λ x/2g d A2；Q為Δt1時間間隔前通過閥門的流量；Q0為閥后初始狀態的流量；f（x+a t）為x處的反射波；f（xl+a（t-（l-x）/a））為Δt2時間間隔前水氣交界面處反射產生的反射波，Δt2=（l-x）/a；Rl-x為衰減系數，Rl-x=λ（l-x）/2g d A2。

需要說明的是，在波追蹤方程的損失項中，考慮水力系統是低摩阻系統［12］且管道波速值大，用Δt1時間間隔前通過閥門的流量代替了流量平均值，當計算的時間間隔取得足夠小時，誤差可忽略。長距離輸水管道計算中，可采用在充水水柱內部增設計算邊界點的方式來保證計算的精度，內部計算邊界點處水錘波的反射和傳播由波守恒定律［11］計算。

水氣交界面作為已充滿段的邊界，在此邊界上由波追蹤方程有：

式中：f為水氣交界面處產生的反射波；F為傳播到此處的初生波；h為交界面壓力水頭；h0為交界面位置水頭，其值為基準高程的相對負值，即當位置高程高于基準高程時取負值，低于基準高程時取正值。當輸水管道隨地勢起伏時，交界面位置水頭將反映管道高程的變化，并將此變化以反射波的形式傳播回泵處。

水氣交界面壓力水頭由管中氣體壓強決定：

式中：p（t）為此時刻的管中氣體絕對壓強；pa為大氣壓強；ρw為水的密度；g為重力加速度。

氣體壓強由氣體狀態方程有：

式中：ρ（t）為此時刻的管中氣體密度；Rg為空氣氣體常數；T為空氣溫度。

氣體密度由質量守恒定律有：

式中：ρ（t-Δt）為前一時刻的管中氣體密度；lg為前一時刻末的管內氣柱長；A為管道橫截面積；Qm，air為氣體出流質量流量；Qw為交界面處充水體積流量；Δt為計算時間步長。

由氣體孔口出流公式［13］，氣體出流質量流量為：

式中：C為孔口出流流量系數；Aout為孔口面積；γ為空氣絕熱指數；p（t-Δt）為前一時刻管中氣體絕對壓強；ρa為大氣密度。

聯立式（5）～（9），可得：

在實際工程中，存在以下兩種典型的特例：

（1）當為短管敞開式排氣時，則p(t) =pa，故有：

（2）當為封閉式管道時，則Aout= 0，故有：

式（10）中，除交界面充水流量Qw外，其余參數皆為已知參數。

水氣交界面處充水流量由波追蹤方程可得：

式中：Qw為水氣交界面處流量；Qw0為水氣交界面處初始狀態的流量。

聯立式（10）、（13），即可求解此時刻水氣交界面處各狀態參數。

同時，輸水管道快速充水，已充水管道長度持續變化，故在整個計算過程中需不斷計算已充水管道長度，由體積法可得：

式中：l0為前一時刻的已充水管道長度；Δt為時間步長。

至此，通過泵閥模型和彈性模型的聯立即可求解泵站空管啟動充水過程，計算流程圖如圖2 所示。水泵轉速未到達額定轉速之前，僅通過插值水泵特性曲線求得機組揚程。當水泵轉速到達額定轉速時，首先由閥門開啟規律求解閥門開度；其次求解泵閥模型得到閥后的流量及水頭，從而可得閥門處的初生波；再次通過式（3）算得一定時間間隔后傳播至水氣交界面處的初生波，然后由式（10）與式（13）聯立求解反射波，再按式（4）計算得到某時刻后重新傳播至閥門處的反射波，用以求解后續時刻的泵閥模型方程。各個時刻管道水柱長度可通過式（14）更新。

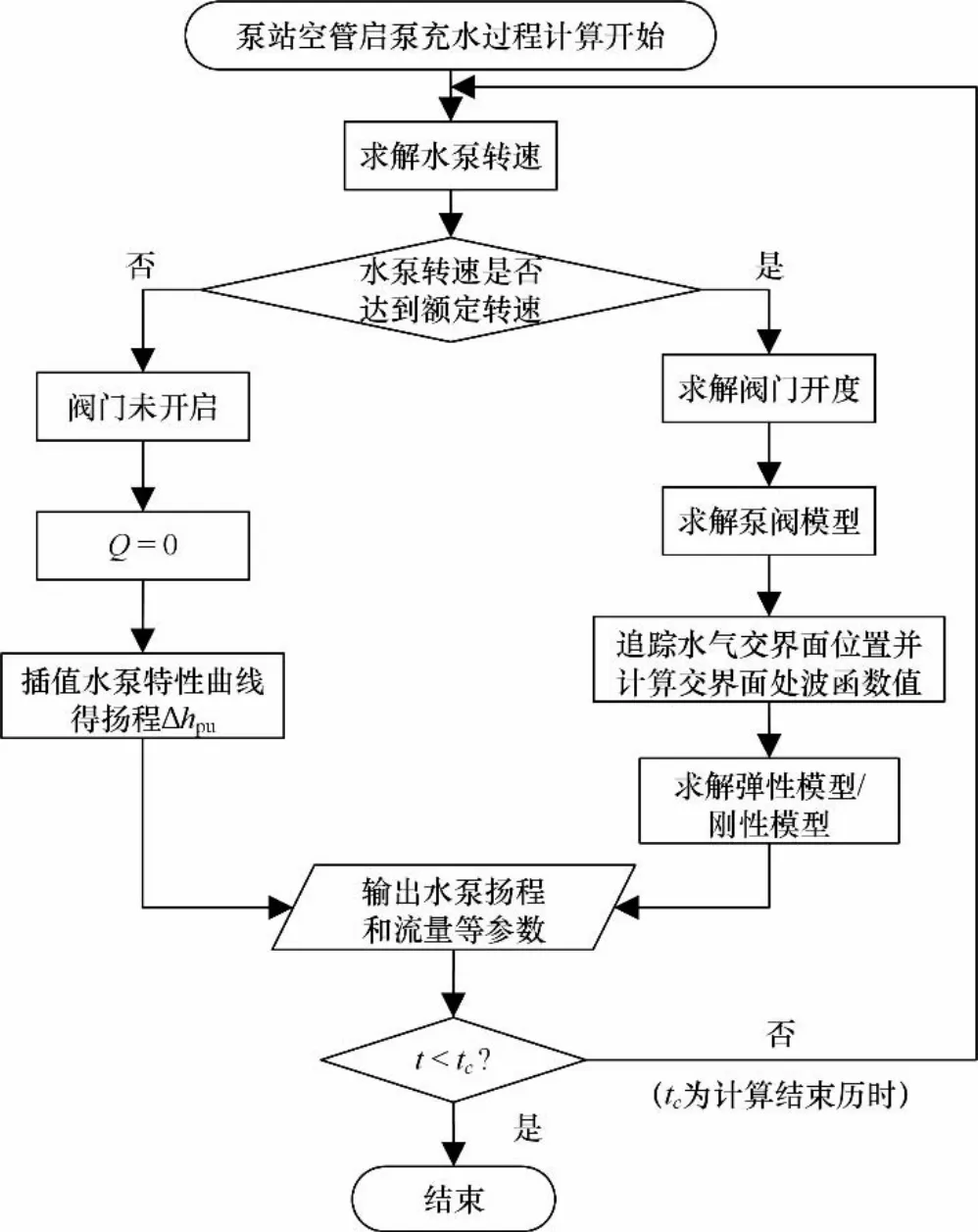
圖2 彈性模型和剛性模型求解計算流程圖Fig.2 Flowchart of the rigid column model and elastic column model

1.3 剛性模型

剛性水錘理論忽略了管壁的彈性并假設計算管路中的水是不可壓縮的，簡便了計算。通常認為剛性水柱模型在閥門開啟歷時Ts＞L∕1 000（L為計算管道長度）時精度是可以接受的［14］，這表明對于較短的空管而言，其計算結果是有意義的。

如圖3 所示，短空管中的水體狀態由連續性方程和動量方程進行描述。

圖3 剛性模型管道主要參數示意圖Fig.3 Pipeline main parameters in the rigid column model

連續性方程：

式中：A為管道截面積；θ為管道傾斜角；hs為自由液面測壓管水頭；Qp為流量。

動量方程：

式中：l為水體長度；hp為1-1 斷面測壓管水頭；f為摩阻系數；D為管道直徑。

對連續性方程及動量方程求積分并取相應近似［12］，有：

與

由波追蹤法的基本方程，可得與短空管串聯的壓力管道連接處1-1的流量、水頭及波參數關系如下：

聯立（17）、（18）、（19）、（20）四式，則得：

同理，hs、hp、fp皆可求得。

由剛性水錘理論，已充水段長度lt與hs有關系式如下：

通過泵閥模型和剛性模型的聯立亦可求解泵站空管啟動過程，計算流程圖如圖2所示。

2 實驗測試

為驗證本文提出的計算模型的準確性，對東雷抽黃工程的南烏牛二級泵站空管啟動充水過程進行現場實驗。南烏牛二級站為單機單管出水的提灌泵站，輸水系統示意圖如圖4所示，主要包括一個進水池和一個出水池，出水池與水泵安裝高程的高程差為107.1 m；一臺水泵機組，其額定揚程為113 m，額定流量為4.57 m3∕s；水泵出水口后設置蓄能罐式液控止回蝶閥和偏心電動半球閥，考慮蝶閥全開時仍將帶來水頭損失，故在計算中將兩個閥門作為一個整體考慮，兩閥門皆全開時水頭損失系數取為0.016；出水管道由直徑為1.2 m、長12 m 的直管及直徑為1.6 m、長365 m 的埋設直管+傾斜管道組成，糙率為0.011，水錘波速為1 000 m∕s。

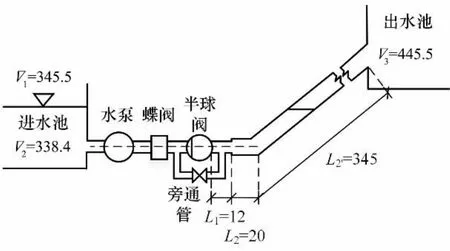
圖4 南烏牛泵站輸水系統Fig.4 Water conveyance system of Nanwuniu pump station

南烏牛二級站半球閥兩側管道用旁通管連接，故在初始時刻，出水管道內水柱自由水面高程與進水池水面高程相等，此高程以下的管道為滿管狀態。在水泵開啟過程中，蓄能罐式液控止回蝶閥全部打開，而偏心電動半球閥先是關閉，當4.5 s 時水泵轉速達到額定轉速后開啟，在30 s 內勻速開至最大開度，閥門開啟過程中的流量特性為直線-等百分比型。當半球閥開啟后，在水泵揚程的作用下，管線開始充水，充水水柱的長度、流速及閥門開度變化如圖5 所示，整個過渡過程中水泵參數的變化見圖6，整個充水過程中，閥門處水錘波函數變化如圖7所示。

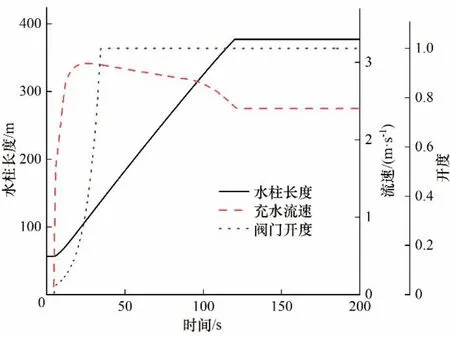
圖5 充水水柱的長度、流速和閥門開度變化過程Fig.5 Change process of water column and valve opening

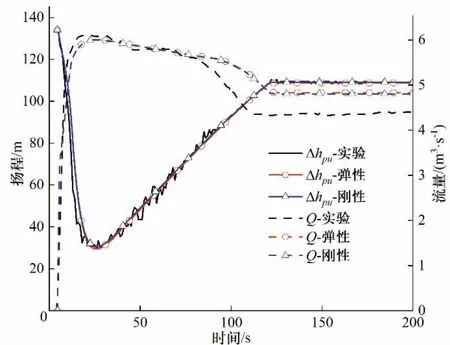
圖6 水泵參數變化過程Fig.6 Change process of the pump parameters

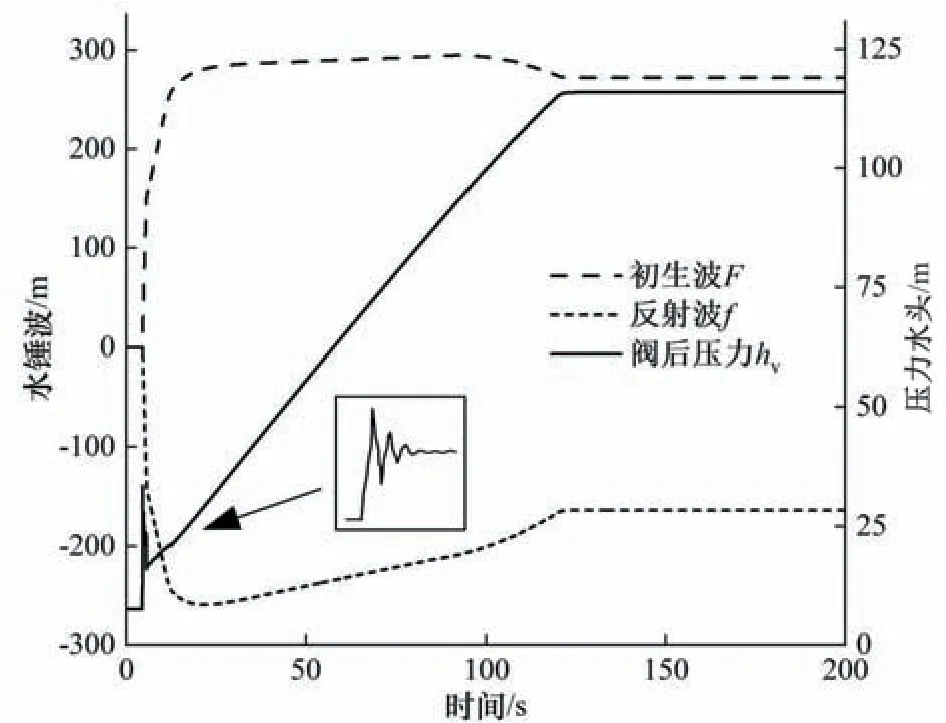
圖7 水擊波參數變化過程Fig.7 Change process of the wave parameters

3 計算和實驗結果分析

從圖5 可知，管內初始水柱長為56.5 m，這是因為南烏牛泵站輸水系統的半球閥前后由旁通管連接，充水開始時在進水池水位相同高程以下的管道皆為滿管。閥門開啟后，管道充水流速先快速上升，在25 s 到達最大值3 m∕s，之后緩慢下降，在90 s左右下降變快，直到122 s 充水過程結束達到穩定的管道出流速度2.4 m∕s。這個過程是水泵的特性導致的，在閥門開啟伊始，閥門兩側壓力差可以視為額定轉速時的關閥揚程，其值約134 m，在此大壓差下，稍一開閥，充水流速就開始迅速上升。

由圖6可以看到，隨著水泵流量迅速增大，水泵揚程快速下降，水泵工況快速變化，電動機功率不斷增大，這一過程在水泵特性曲線上的表現即為工況點快速掃掠形成過渡過程線。隨著流量的不斷增大與水泵揚程的不斷下降且充水水柱自由液面高程逐漸爬升，在25 s 時閥門前后壓差恰好等于閥門局損，流量不再增加，此時水泵流量到達最大值6 m3∕s，水泵揚程亦到達最小值29.5 m，功率達到最大值，若此時充水過程恰好結束，充水水柱自由液面不再上升，那么輸水系統各項參數將就此達到穩定。但從圖5 看到，此時充水水柱長度剛剛到達109.5 m，充水過程遠未結束，故隨著自由液面不斷升高，閥后壓力水頭增大，閥門前后壓差減小，管道充水流速、水泵流量下降，水泵揚程不斷回升以保持流量趨向穩定。在這種水面高程、水泵流量與揚程的共同作用下，管道充水不斷進行，充水過程在122 s時完成。此后水泵揚程與流量保持穩定，穩定工況水泵揚程為108.6 m，水泵流量為4.84 m3∕s。

由圖6 可知，兩種模型計算得到的結果與實驗測得的物理過程一致，彈性模型和剛性模型的計算結果相差很小，這是因為南烏牛泵站出水管道為低摩阻短管，且波速較大，整個過渡過程剛性模型計算的精度是可行的，因考慮管道和流體彈性而計入的損失是有限的。在空管充水過渡過程中，水泵揚程變化曲線基本重合，表明基于波追蹤法建立的數學模型計算結果能準確地反映整個水力過渡過程。然而，計算與實驗得到的水泵流量變化不完全重合，其原因是計算時采用的是水泵出廠時的特性曲線，而實際上南烏牛泵站的水泵機組已運行多年，水泵特性不可避免地發生一定的變化，正是這種水泵機組特性差異導致了計算結果與實驗結果的差異。從圖6 差異段可以分析，在高效區附近，相同的水泵揚程下，水泵的輸水流量變小，即水泵效率下降，這是符合泵站運行規律的。

圖7 為波追蹤法計算得到的閥后波參數變化過程，從中可以看出，在閥門開啟后，由于流量的增大，輸水管道中產生一個升壓波F，由于管內水柱短且波速大，此升壓波經傳播-反射-傳播后又以降壓波f的形式到達閥門處，中間時間間隔很短。在整個充水過程中，閥后壓力水頭體現了初生升壓波F與反射降壓波f的共同作用，閥門甫一開啟，由于反射波尚未產生，在閥后產生一個明顯的壓力上升，當反射波不斷傳播回閥門處，壓力上升即得到抑制；隨著管道充水的進行，閥后壓力水頭不斷上升，當充水過程結束，初生波、反射波及壓力水頭也到達穩定。從壓力的角度分析，初生波與反射波的共同作用是以靜壓形式存在的。

4 結 論

（1）建立了基于波追蹤法的計算泵站空管啟動充水過渡過程的彈性和剛性計算模型，通過實驗驗證了模型的可靠性，計算結果表明運用兩種模型均能準確地求解泵站短空管啟動充水的水力過渡過程。

（2）閥門開啟后出現流量急劇上升、揚程減小、功率增大的情況，泵站空管啟動充水應優化工作閥門開啟規律，避免電動機過載。

（3）管道充水過渡過程中，工作閥門后的壓強水頭為初生波和反射波共同作用的結果。