追鉤防搖原理模型及算法
王君雄,段盼盼
(三一海洋重工有限公司,廣東 珠海 519000)
0 引言
防搖控制主要有開環防搖與閉環防搖兩大類型。開環防搖往往采用前饋控制方法進行控制,這種方案實現簡單,價格便宜,可操作性強,但是防搖精度低,抗干擾能力差,不可變擺長,初始條件必須為0 等限制,因此只適合于車間、小擺長的情況。而對于類似于場橋、岸橋這種大型場外設備,擺長相對較長,且外場干擾因素多,因此,此類場景的方案均主要為閉環防搖,控制模型均基于單擺模型[1-4]。
然而,針對實際的場橋、岸橋吊裝作業過程中,有經驗的操作手大部分采用追鉤的方式來防止吊具搖擺。從實踐效果看,使用該方式不僅能很好地減搖,熟練的操作手還能做到較高精度地控制吊具位置。
1 追鉤防搖的原理
追鉤防搖原理[5]可概括如下:
計算吊具的擺動幅度和方向:通過對傳感器數據的處理和分析,可以計算出吊具的擺動幅度和方向。采用控制算法對吊具進行控制,根據吊具當前的狀態和期望狀態之間的差異,計算出小車需要移動的距離和方向。
控制小車移動:將計算出的移動距離和方向通過電機控制器,控制小車沿軌道移動,從而使吊具保持在垂直狀態。
反饋控制:通過反饋控制,不斷地檢測吊具的狀態,并根據吊具當前的狀態和期望狀態之間的差異,對小車進行調整,保持吊具穩定。
2 追鉤防搖的模型及算法
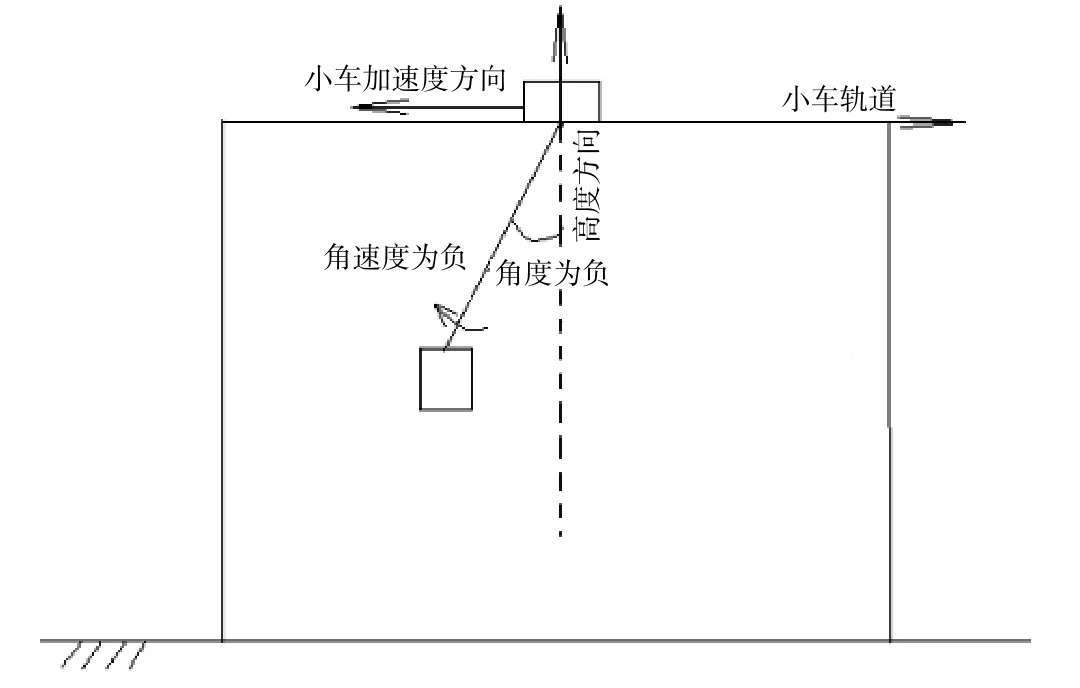
分析場橋、岸橋這類門式集裝箱起重機,小車帶動吊具平移的作業場景,當小車在軌道上行走,鋼絲繩連接吊具帶著吊重,此時吊具及吊重發生擺動,即載荷擺動。可以簡化為如圖1 所示模型。
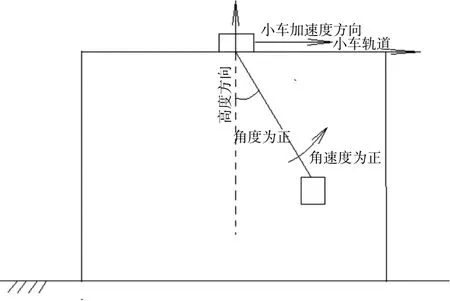
圖1 吊具擺動模型
如圖1,可得對于定擺長防搖控制其控制方程為:
式中,l為單擺的擺長為角加速度;y為擺動角度;g為重量加速度;f(t)為小車加速度
令其齊次方程解為:r = u + vi
可得[5]
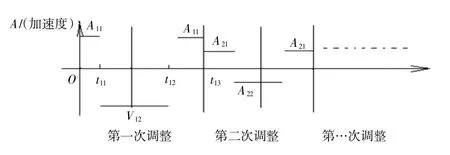
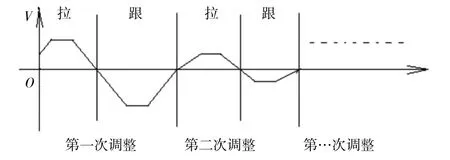
令:f(x)=,即在0 分段擺動方程為: 取t= 0 時,擺動角度為θ0,角速度為ω0,可得: 若要使得T≤t時擺動為0,即 f1(x)滿足以下條件: S為當前位置與目標位置的距離。 在防搖控制中f1(x)為加速度,由于實際項目中一般為速度控制,因此可以通過規劃速度控制率反推加速度控制率。可選擇的速度控制曲線較多,我們選擇較方便可鋸齒形調節方式進行減搖,如圖2 所示(橫軸為時間軸): 圖2 鋸齒型調節速度及加速度變化 式中:Aij為第i次調整的第j個加速度;i?N+為第i次調整;j?N+為某次調整中的第j個加速度;Vij為第i次調整的第j個速度;i?N+為第i 次調整;j?N+為某次調整中的第j個速度;tij表示第i次調整的第j個時間點;i?N+,表示第i次調整;j?N+,表示某次調整中的第j時間點。 (8)式代入(6)(7)式可得: 參數滿足如下條件: 選擇倒U 型調節方式減搖,則如圖3 所示(橫軸為時間軸): 圖3 倒U 型調節速度變化 參數滿足如下條件: 對于追鉤防搖控制,一般不對目標位置做特殊要求,因此在不考慮調整距離的情況下,可考慮2 種特殊條件下的控制。 由條件1 可得: 即可得: 若要使得則t13> 0,ω0θ0> 0:可分為兩種情況: 情況一,ω0> 0 時,θ0> 0,此時:A11> 0,如圖4所示。 圖4 條件1 下擺動角度為正時跟吊具示意圖 情況二,ω0< 0 時,θ0< 0,此時A11< 0,如圖5 所示。 圖5 條件1 下擺動角度為負時跟吊具示意圖 由條件2 可得: 即: 若令:vt2= π,則: 若要使得t13> 0 則:ω0θ0> 0,可分為兩種情況: 情況一,ω0> 0 時,θ0> 0,此時A11> 0,如圖6、圖7 所示。 圖6 條件2 下擺動角度為正時拉吊具示意圖 圖7 條件2 下擺動角度為正時跟吊具示意圖 情況二,ω0< 0 時,θ0< 0,此時:A11< 0,如圖8、圖9 所示。 圖8 條件2 下擺動角度為負時拉吊具示意圖 圖9 條件2 下擺動角度為負時跟吊具示意圖 集裝箱起重機實驗設備實際應用,驗證上述追鉤防搖控制算法,可以觀察到看到采用此方式,可以有效地抑制吊具及吊重的搖晃效果呈現,如圖10 所示。 圖10 吊具追鉤防搖效果 本研究旨在探究門式集裝箱起重機司機追鉤的原理,并驗證追鉤防搖的效果,為起重機操作手的培訓及吊具吊重的防搖控制提供新思路。通過仿真和實驗觀察,揭示了司機追鉤的原理,并通過仿真計算和實際設備驗證了追鉤防搖的效果。3 控制器設計
3.1 鋸齒型防搖控制率

3.2 倒U 型運動控制率
4 控制參數優化
4.1 條件1:t11=0,A11=A12

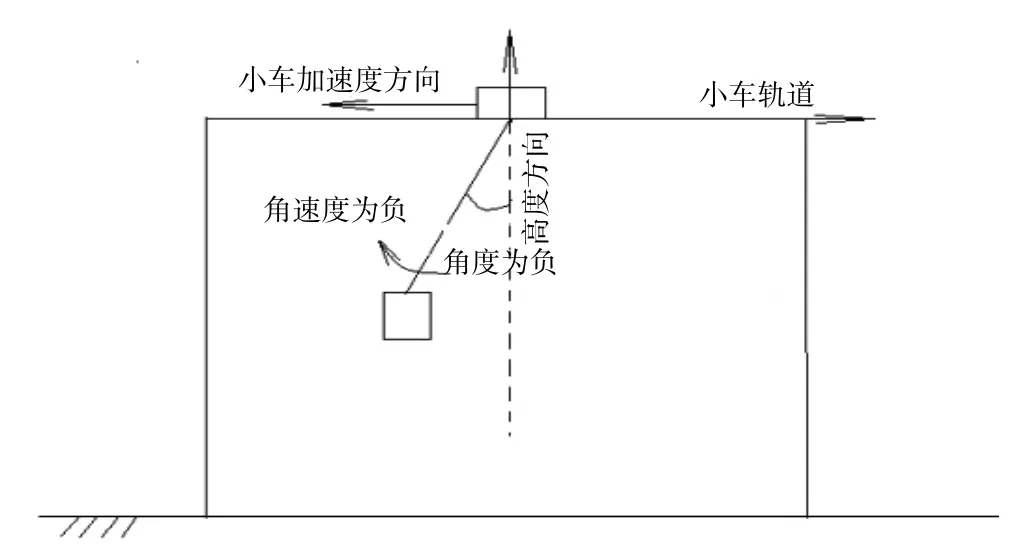
4.2 條件2:t11=0,A11=-A12



5 算法驗證

6 結語

