基于改進人工水母搜索算法的電液伺服系統控制研究
付榮赫,秦泰,張奇,邢吉生
(北華大學電氣與信息工程學院,吉林吉林 132021)
0 前言
電液伺服系統因高度可控性和高效性已被廣泛應用于工業制造、航空航天等領域[1],系統能否穩定運行取決于其傳動部分是否穩定,進而直接影響到其實際應用。因此,運用自動化技術、智能算法等實現電液伺服系統精確、穩定控制,對提升系統的運行效率以及產品的質量等具有非常重要的意義。
電液伺服系統主要由動力部分和電信號處理部分組成,可用小功率電信號來控制大功率傳動元件[2]。但它是一個復雜的非線性系統,含有時變不確定性和擾動性,PID傳統控制方法受自身局限性約束,很難在復雜系統中整定出理想的最優值,使得其控制效果不佳,已不能滿足系統所需的控制要求[3]。
現如今,隨著學者們對智能算法的深入研究,眾多群智能算法被引入到PID參數整定優化問題中[4],但算法中的問題也逐步顯現出來。比如人工水母搜索[5](Artificial Jellyfish Search,AJS)算法存在易陷入局部最優等問題,為了解決這些問題,本文作者提出將蝴蝶優化算法(Butterfly Optimization Algorithm,BOA)中的隨機移動概念引入AJS算法中優化PID參數,在保留算法簡單、易實現的基礎上,通過增強個體位置多樣性提高算法的精度、全局搜索能力等。
1 電液伺服系統數學模型
在工業制造領域,電液伺服系統具有反應速度快、靈敏性高等優點,在注塑機運行時提供較準確的控制。系統主要由指令裝置、液壓缸、傳感器、伺服電磁閥和動力裝置組成[6],結構如圖1所示。
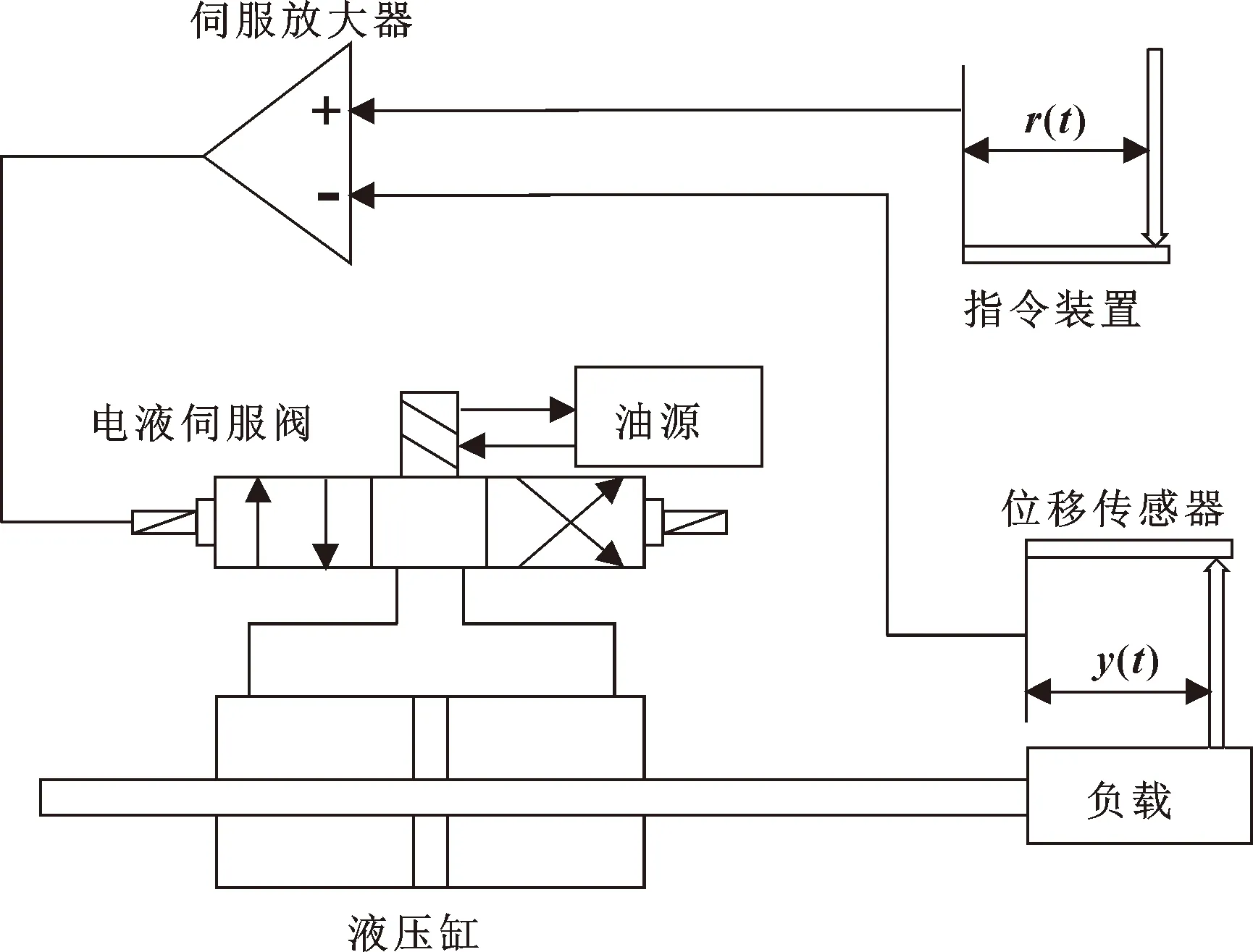
圖1 電液伺服系統結構
該系統由指令裝置給定指令電位,輸入位置信號經控制器、伺服放大器等到達電液伺服閥,位置反饋將輸出位置信號反饋回比較元件,產生誤差信號后輸入控制器,進而控制液壓缸的位移[7]。其控制原理如圖2所示。
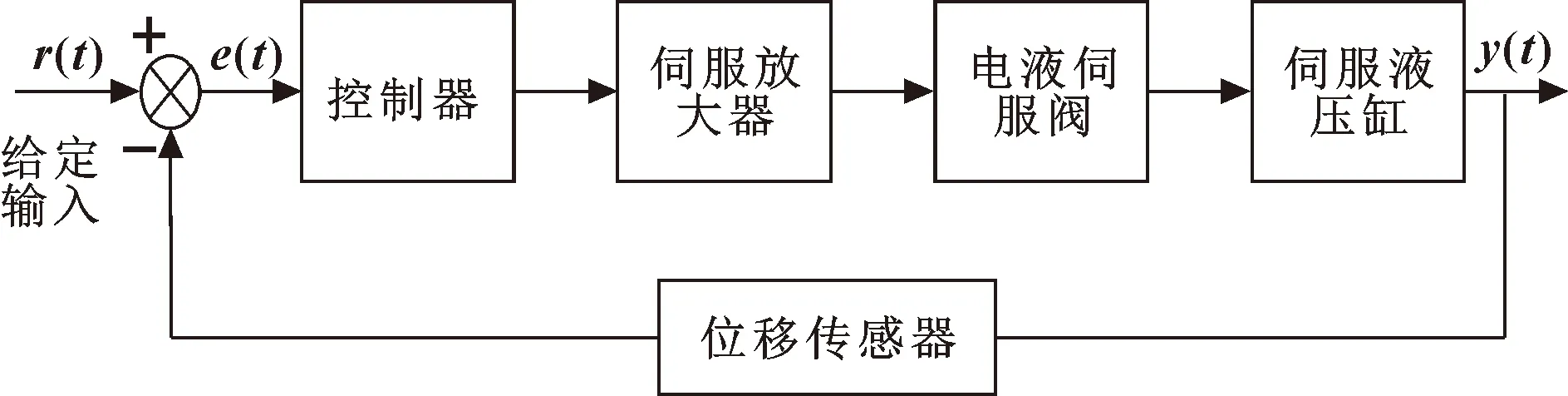
圖2 系統控制原理
電液伺服系統的運動微分方程[2]為
(1)
(2)
xv=KvKSu
(3)
式中:Ap為活塞面積;xp為活塞位移;Ct為總泄漏系數;p1為負載壓差;Vt為總壓縮容積;KQ為流量增益;xv為閥芯位移;Kc為壓力系數;βe為彈性模量;mt為活塞上總質量;cp為黏性阻尼系數;FL為負載力;k為彈簧剛度;Kv為控制器增益;KS為伺服閥增益;u為控制電壓信號。
在控制電壓u的作用下,其動態方程[1]為
(4)
式中:ξ為閥門阻尼比;ωn為閥門固有角頻率;η為閥門增益。
創建良好的系統數學模型,是獲得傳遞函數的關鍵[8]。對系統的輸入以及輸出的數學模型進行分析,得出伺服閥的傳遞函數為
(5)
2 人工水母搜索算法
人工水母搜索算法(AJS)是模擬自然界水母覓食搜尋行動的一種隨機搜索算法。在水母覓食過程中,涉及到水母與洋流、水母在水母群中的運動(主動運動和被動運動),這些運動之間通過時間控制機制進行切換,以及匯聚成水母群的過程[9]。
在AJS算法中,存在以下2種假設:水母可以跟隨洋流,也可以在群體內部移動,而時間控制機制管理著這些移動類型之間的轉換;水母在海洋中移動尋找食物,它們更容易被吸引到食物供應量更大的地方。
2.1 洋流對水母位置的影響
洋流中含有大量的營養物質,因此水母才被吸引過來。洋流的方向由海洋中每只水母到目前位于最佳位置的水母的所有向量平均值決定,公式如下:
(6)
t=X*-df
(7)
df=ecu0
(8)
其中:npop為水母數量;X*為當前水母種群的最優位置;ec為控制吸引力的因子,由式(9)確定;u0為所有水母的平均位置;df為目前水母最佳位置和所有水母的平均位置之間的差異,由式(10)確定。
ec=β·rand(0,1)
(9)
df=β·rand(0,1)·u
(10)
每只水母的新位置:
Xi(t+1)=Xi(t)+rand(0,1)·t
(11)
將式(7)、式(10)代入式(11)中,即:
Xi(t+1)=Xi(t)+rand(0,1)·(X*-β·
rand(0,1)·u)
(12)
式中:β為分配系數,取值為3。
2.2 水母群對水母位置的影響
類型A運動是水母圍繞其位置的運動,每個水母的相應更新位置:
Xi(t+1)=Xi(t)+γ·rand(0,1)·(Ub-Lb)
(13)
式中:Ub和Lb是搜索空間的上限和下限;γ為運動系數,取值為0.1。
為了模擬B型水母的運動,隨機選取一只水母j作為感興趣的水母,水母i至選定的水母j的矢量確定其運動方向。當選定的水母j所在地點的食物數量超過水母i所在地點的食物數量時,則后者朝前者移動;反之,則后者遠離前者。因此,每只水母都朝著更好的方向移動,尋找群體中的食物。水母的運動方向和更新的位置公式如下:
S=Xi(t+1)-Xi(t)
(14)
whereS=rand(0,1)·D
(15)
Xi(t+1)=Xi(t)+S
(16)
(17)
時間控制公式如式(18)所示:
(18)
式中:t為迭代次數;nmax為最大迭代次數。
2.3 種群初始化
水母位置初始化如式(19)所示:
Xi(t+1)=ηXi(1-Xi) 0≤X0≤1
(19)
式中:Xi為第i類水母的Logistic邏輯混沌值;X0∈[0,1]為水母初始位置范圍,但X0≠0,0.25,0.75,0.5,1.0,η=4.0。
2.4 邊界條件
海洋分布在全球各地,因此當水母移出有界的搜索區域時,它會回到相反的界限:
X′i,d=(Xi,d-Ub,d)+Lb(d) ifXi,d>Ub,d
(20)
X′i,d=(Xi,d-Lb,d)+Ub(d) ifXi,d (21) 式中:X′i,d為更新后的水母位置;Xi,d為第i只水母在d維的位置;Ub,d和Lb,d為搜索空間的上下限。 針對AJS算法存在易陷入局部最優等問題,提出改進策略,將蝴蝶算法[10]融入到AJS算法中,來增強全局搜索能力和收斂精度,形成改進人工水母(Improved Artificial Jellyfish Search,IAJS)算法。此次改進策略是將蝴蝶算法里蝴蝶全局搜索階段的思想引入到AJS算法中,對其個體位置進行更新。此方法可增強類型A運動水母位置的多樣性。位置更新公式如式(22)所示: Xi(t+1)=Xi(t)+γ·rand(0,1)·(Ub-Lb)+ (22) 式中:g*為目前為止的最優解;fi為水母的發光點;r∈[0,1],為隨機數[11]。 算法的詳細步驟為:(1)初始化水母種群;(2)評估適應度值確定初始最優位置;(3)更新時間控制參數c(t);(4)根據洋流更新水母位置;(5)更新運動類型,分別更新類型A和B的水母位置;(6)重新評估適應度值及更新水母最優位置;(7)判斷是否滿足最大迭代次數,若滿足,則輸出最優位置和全局最優解,否則,返回步驟(3)重新迭代計算。 PID控制由PID控制器和被控對象所構成,而PID控制器由三部分構成,分別為比例、積分和微分等,其應用格外廣泛,控制規律如式(23)所示: (23) 式中:e(t)是系統誤差;Kp、Ki、Kd分別對應PID控制器中3個部分的系數,通過調整這3個系數,找到其最優值,就能得到較好的控制成果,達到改善控制性能的目的[12-15]。將IAJS算法用于PID參數整定原理如圖3所示。 此次以某型號注塑機為例,將系統主要參數代入式(5)所示的傳遞函數中,得到系統仿真模型為 (24) 此系統為典型的二階系統,在MATLAB軟件中仿真控制系統的傳遞函數,它在Simulink環境下仿真圖如圖4所示。 圖4 Simulink環境下PID仿真圖 為驗證文中所提出算法的優劣性,分別選用IAJS、AJS和PSO算法對系統進行PID控制器的參數優化。為了方便比較3種算法,設置其輸入為單位階躍信號,仿真時長設為15 s,采樣時長為0.001 s,迭代次數為100次。 采用不同算法進行多次迭代后輸出其適應值收斂曲線如圖5所示。可知:隨著迭代次數的增加,IAJS算法在迭代次數為23次時,適應值收斂并精度較高,而AJS和PSO算法分別迭代到26次和28次時適應值收斂,因此IAJS展現出了精度高等優勢。 圖5 算法收斂曲線 輸出IAJS算法優化PID參數變化曲線如圖6所示。Kp、Ki、Kd這3個參數大約經23次迭代后輸出最優值,IAJS算法在前期表現出卓越的全局收斂能力,并且于迭代次數較少的情況下能得到較高的精度。 圖6 IAJS優化PID參數曲線 將3種算法優化所得的參數值依次代入控制系統的PID控制器中,并在MATLAB中運行,得出響應曲線如圖7所示。可知:標準PSO的上升時間短,進而導致PSO的響應速度快于IAJS算法,但在超調量、穩態誤差等方面IAJS明顯更少。 圖7 階躍響應輸出曲線 此外,IAJS算法到達穩定所用的調節時間為2.12 s,優于AJS和PSO算法穩定的調節時間2.45 s,因此系統的調節速度更快,能很快達到穩定狀態。經過IAJS優化的PID最佳參數,選出的3個K值恰當,將調節時間和超調量等優化到盡可能小,使系統得到良好的控制效果,因而證明此方法的可行性。 在t=10 s時引入一個單位的階躍擾動,輸出響應曲線如圖8所示。可知:系統受到階躍擾動后都會產生短暫的震蕩,擾動消除后系統逐步恢復穩定,文中所提出的IAJS算法相比于其他2種算法有較出色的抗干擾能力,同時也展現出更優越的控制效果。 圖8 加入階躍擾動后響應曲線 文中以電液伺服系統為研究對象,針對常規PID控制存在參數調節時間長等問題,提出了運用IAJS優化PID參數的方法,并驗證了引入蝴蝶隨機移動概念后的IAJS算法通過增強位置多樣性后能有效改善AJS算法易陷入局部最優等缺點的可行性。通過對比3種算法參數整定優化的結果,在控制效果、調節時間、性能指標和穩定性等方面,IAJS算法比其他2種方法效果更好,顯著提高了系統的穩定狀態,有效地提升了系統的性能和運行穩定性。這就使得其在航空航天、機床控制以及振動環境模擬系統等領域應用更為廣泛,對于減少設備的過載損壞、提升設備的使用壽命以及節能減排等方面有著廣闊的應用前景。3 改進人工水母算法
3.1 改進策略
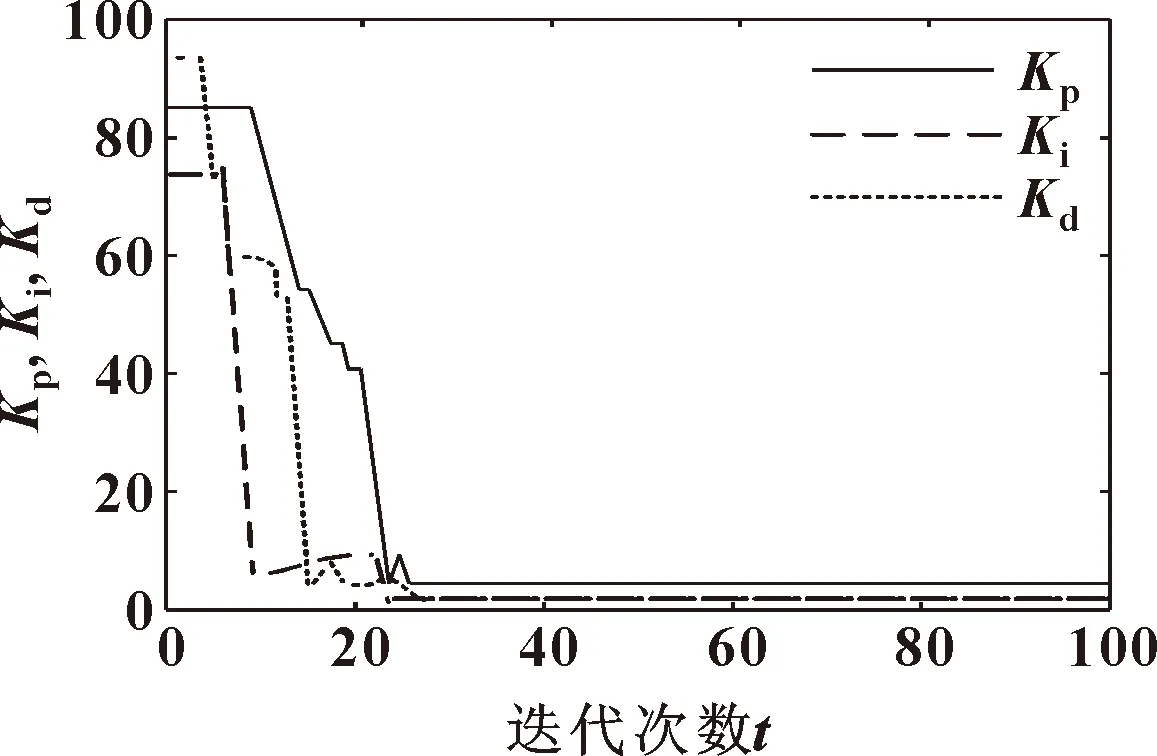
3.2 改進人工水母算法PID設計
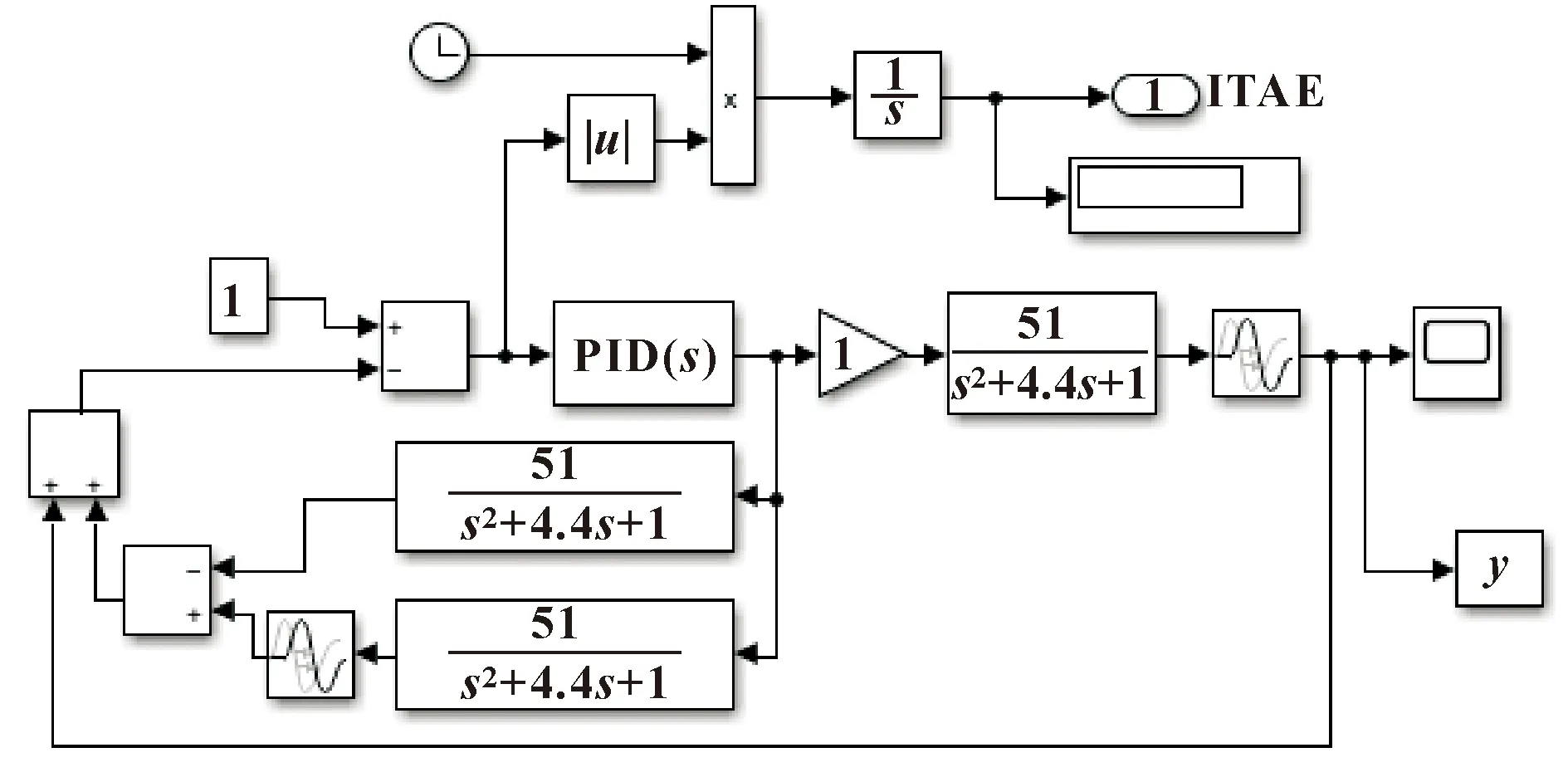
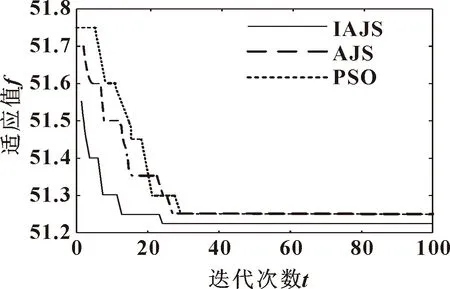
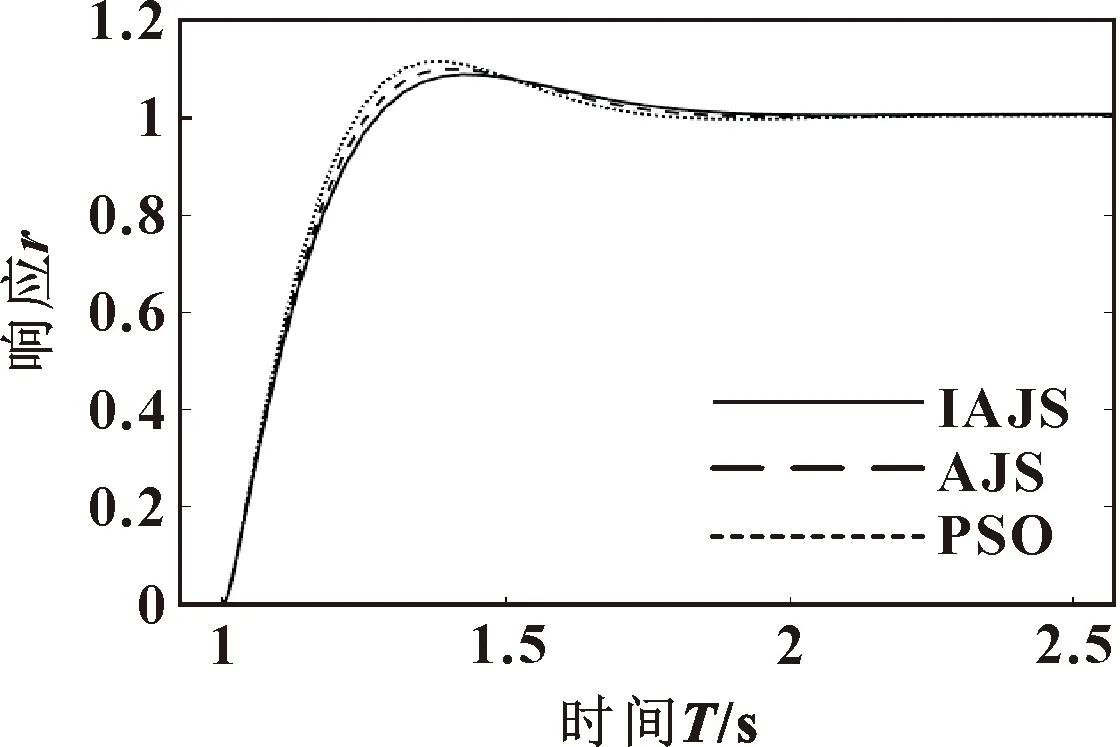
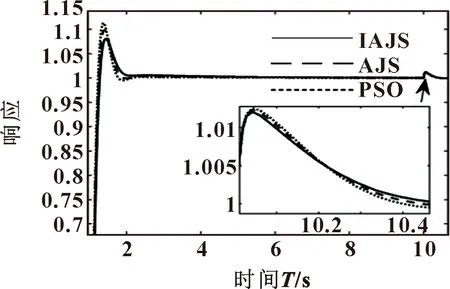
4 仿真結果與對比分析
5 結論

