基于齒形鏈銷軸-鏈板接觸副的熱混合潤滑分析*
周亞林 劉曉玲 朱鵬娟 何文卓 劉國梁
(青島理工大學機械與汽車工程學院 山東青島 266520)
隨著工業的不斷發展,齒形鏈的工程應用越來越廣泛,齒形鏈銷軸-鏈板副工作在純滑動條件下,摩擦產生的熱效應不可忽略。同時銷軸-鏈板接觸副表面并非是理想光滑的,尤其在惡劣的環境中,難免由于灰塵等微小顆粒的影響,導致接觸表面出現磨痕甚至劃痕,故應考慮表面粗糙度。李海玲和魏引煥[1]分析了齒形鏈輪的嚙合機制,研究了齒形鏈與鏈輪嚙合參數的設計并計算了嚙合時的沖擊速度。金麗君和付振明[2]采用不同的熱處理方法對齒形鏈中的銷軸和鏈板進行熱處理,在含介質油潤滑條件下,研究了新型齒形鏈的耐磨性。ZHANG等[3]建立了有限長線接觸穩態熱彈流潤滑模型,對齒形鏈中的銷軸-鏈板接觸副進行了有限長線接觸熱彈流潤滑分析。然而,上述文獻未涉及混合潤滑條件。針對混合潤滑的研究,JOHNSON等[4]首先引入了載荷分享的概念,即負載由流體和粗糙峰共同承擔。基于載荷分享機制考慮粗糙表面接觸變形的統計學模型,王志堅等[5]建立了耦合粗糙峰接觸彈塑性變形與邊界膜摩擦化學效應的有限長線接觸熱彈流混合潤滑模型,探討了表面粗糙度和潤滑油性質對接觸副潤滑性能的影響。周江敏等[6]基于平均流量模型,建立了線接觸非牛頓混合潤滑模型,研究了表面粗糙度和熱效應的影響。由于齒形鏈常用于重載工作環境中,且銷軸-鏈板副接觸副處的接觸面并不是理想光滑的,為使研究更貼近齒形鏈實際工況,有必要考慮混合潤滑條件[7]。
綜上所述,目前關于齒形鏈摩擦磨損的理論和實驗研究較多,并且大多是探討從其幾何結構上進行優化,然而針對重載工況下齒形鏈的混合潤滑性能研究尚不多見。為此,本文作者結合齒形鏈中銷軸-鏈板接觸副的幾何關系及其運動特性,建立了銷軸-鏈板副的熱混合潤滑模型,分析了齒形鏈銷軸-鏈板副的綜合曲率半徑、表面粗糙度和載荷對非牛頓熱混合潤滑性能的影響。
1 幾何模型
1.1 鏈板相對銷軸滑動速度分析
齒形鏈的嚙合原理見圖1,p為鏈節節距;n1為鏈輪的轉速;θ為相鄰鏈板之間的轉角,θ=2π/z[1];r為鏈輪分度圓半徑。

圖1 齒形鏈的嚙合原理
圖2表示的是齒形鏈工作時的速度分析。圖中,α為鏈節在鏈輪上的相位角;U為鏈節的分度圓速度,U=ω1r;U1、U2分別為水平速度和豎直速度。

圖2 齒形鏈的速度分析
設齒形鏈鏈輪齒數為z,則分度圓半徑為
設一節鏈板嚙合區域長度為一個節距p,則其嚙合的時間為
銷軸-鏈板副的運動關系如圖3所示,ra為鏈板孔半徑;rb為銷軸半徑;ω2為鏈板繞銷軸轉動的角速度。

圖3 銷軸-鏈板接觸副示意
設銷軸固定,其線速度ub=0,由于齒形鏈經過一節鏈板嚙合區域長度p所用的時間,與相鄰鏈板之間的轉角θ所用的時間Δt相同,則在齒形鏈工作時的嚙合或脫合區,鏈節繞某一銷軸轉動的角速度為
則鏈板繞銷軸轉動的線速度為
ua=ω2ra
(4)
銷軸-鏈板副的卷吸速度為
1.2 銷軸和鏈板接觸副綜合曲率半徑
由于銷軸柱面和鏈板內孔的接觸為共形面,故銷軸和鏈板接觸副的綜合曲率[8]可表示為
1.3 銷軸和鏈板接觸副載荷的計算
假設銷軸單位長度上的載荷為w,但由于鏈板與導板的寬度不同,故銷軸兩側單位長度上的載荷分別用w1和w2表示,見式(7)。這里w1、w2均取為平均值。如圖4所示,L1為鏈板寬度,L2為導板寬度,F為齒形鏈的單邊張緊力。
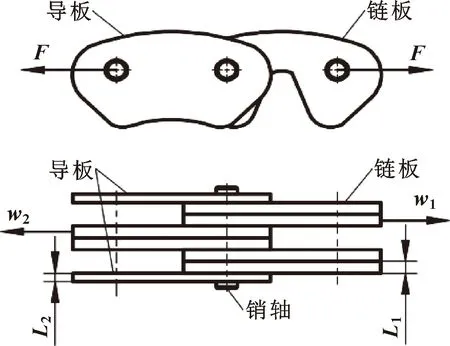
圖4 銷軸的載荷分析
2 數學模型
2.1 混合潤滑模型
設潤滑油為Ree-Eyring非牛頓流體,其等效黏度為
式中:η*表示等效黏度;η表示Ree-Eyring非牛頓流體表觀黏度;τ0表示Ree-Eyring流體特征剪應力;τ表示流體剪切應力[8]。
根據混合潤滑的壓力分享制機制得,總壓力pt可由油膜壓力ph和粗糙峰壓力pa兩部分組成:
pt=ph+pa
(9)
粗糙峰接觸時的油膜分布如圖5所示。對于粗糙度符合高斯分布的表面,hT的表達式[9]為

圖5 粗糙峰接觸時的油膜分布
式中:hT為銷軸-鏈板鉸鏈副兩表面間的平均間隙;h為油膜名義厚度,可由式(11)求得。
式中:h00為銷軸柱面、鏈板孔表面的彈性趨近量。
2.1.1 Reynolds方程
考慮表面粗糙度時的無限長線接觸非牛頓流體Reynolds方程為
式中:φx為壓力流量因子。
在粗糙度符合高斯分布的各向同性的表面上,由PATIR和CHENG[10]推導出的壓力流量因子φx的表達式為
φx=1-0.9e-0.56(h/σ)
(13)

式中:η為流體的表觀黏度;ρ為流體密度。
Reynolds方程的邊界條件為
式中:xin、xout分別表示油膜入口、出口區的計算域邊界。
2.1.2 黏度、密度分別與壓力-溫度之間的關系
表觀黏度η可由Roelands黏壓-黏溫關系[11]求解,其表達式為
η=η0exp{A1[-1+(1+A2ph)α(A3t-A4)-β]}
(16)
式中:η0表示環境條件下的黏度;α表示黏壓系數;β表示黏溫系數;A1=lnη0+9.67,A2=5.1×10-9Pa-1,A3=1/(t0-138) K-1,A4=138/(t0-138)。
密度ρ可由Dowson-Higginson密壓-密溫關系式[12]求解,其表達式為
式中:ρ0表示環境密度;C1=0.6×10-9Pa-1,C2=1.7×10-9Pa-1,C3=6.5×10-4K-1。
2.1.3 潤滑油及兩固體的能量方程
潤滑油的能量方程為
式中:c、k分別為潤滑油的比熱容、熱傳導系數;u為油膜的平均流速;Qa為由粗糙峰接觸所產生的單位體積的熱量。
式中:粗糙峰接觸時的滑動速度us=ub-ua;fa為兩表面粗糙峰相接觸時的滑動摩擦因數。
兩固體的能量方程為
式中:ca,b、ρa,b和ka,b分別為鏈板和銷軸的比熱容、密度和熱傳導系數。
固體a、b與油膜界面的溫度應滿足界面熱流量連續條件:
2.1.4 載荷平衡方程
由載荷分享機制,載荷的平衡方程可寫為

(22)
式中:w為銷軸-鏈板接觸副所承受的載荷。
2.2 粗糙峰模型
2.2.1 粗糙峰接觸壓力
由ZHAO等[13]提出的彈塑性模型,表面粗糙峰接觸壓力可表示為
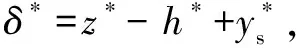
根據MCCOOL[14]的研究,σs和ys的計算表達式為
2.2.2 銷軸-鏈板接觸副處摩擦因數的計算
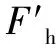
因此,在混合潤滑計算域內的平均摩擦因數可表示為
fc=F′/w
(27)
3 數值方法

油膜壓力的求解與膜厚方程中彈性變形的求解分別采用多重網格法與多重網格積分法,溫度場的求解采用逐列掃描法。網格層數為6,其中最高一層網格節點數為961個節點,計算域的起點與終點坐標分別為Xin=-4.6,Xout=-2.4。
數值計算流程如圖6所示。

圖6 計算流程
首先,輸入速度、滑滾比等參數,然后,計算總壓力和溫度的初值,計算彈性變形、油膜厚度、粗糙峰接觸壓力,求解Reynolds中的參數,進而求解油膜壓力及總壓力,計算總壓力相對誤差、載荷相對誤差及溫度相對誤差。當壓力相對誤差εPt與溫度相對誤差εT<1×10-4,載荷相對誤差εW<1×10-3時達到收斂精度,跳出循環,最后,計算平均摩擦因數,并輸出結果。
4 計算結果及分析

輸入必要參數:銷軸-鏈板是鋼-鋼接觸,材料參數G=5 000,設銷軸-鏈板副的滑滾比S=1.5;βT=σ/0.01,t0=303 K(30 ℃),hd=0.01E′,fa=0.15。對于潤滑油:η0=0.08 Pa·s,c=0.14 J/(kg·K),β=4.76×10-2K-1,τ0=10 MPa,ρ0=870 kg/m3,α=2.19×10-8m2/N,k=2 000 W/(m·K)。對于銷軸a和鏈板b:ca,b=470 J/(kg·K),ρa,b=7 850 kg/m3,ka,b=46 W/(m·K)。
4.1 算法驗證
為了驗證文中鏈銷軸-鏈板接觸副的熱混合潤滑模型的正確性,與文獻[6]輸入參數相同,即滑滾比S=0.5,載荷參數W=1×10-4,速度參數Ue=1×10-11,將文中與文獻[6]模型的計算結果進行了比較,如圖7所示。可見,對于表面粗糙度對總壓力、油膜壓力和粗糙峰接觸壓力的影響,文中模型與文獻[6]模型中的結果一致,驗證了文中模型的正確性。

圖7 算法的驗證
4.2 綜合曲率半徑對潤滑特性的影響
在表面粗糙度σ=0.4 μm、載荷參數W=5.19×10-6(pH=0.21 GPa)時,膜厚比λ(λ=hmin/σ)隨綜合曲率半徑r0的變化趨勢如圖8所示。隨著綜合曲率半徑的增加,膜厚比λ不斷增加。當0<λ<1時處于邊界潤滑狀態,當1<λ<2.5時處于混合潤滑狀態,當膜厚比λ>2.5時處于全膜潤滑狀態。由圖8可知,當綜合曲率半徑r0約100 mm時,銷軸-鏈板副由混合潤滑狀態向全膜潤滑狀態過渡。

圖8 膜厚比λ隨綜合曲率半徑r0的變化趨勢
與圖8工況下一致,圖9給出了混合潤滑條件下的總壓力pt、油膜壓力ph和粗糙峰接觸壓力pa隨綜合曲率半徑r0變化。可見,隨著綜合曲率半徑的增加,總壓力與油膜壓力均增加,而粗糙峰接觸壓力減小。這是因為對應圖8,當綜合曲率半徑增加時,銷軸-鏈板副由混合潤滑狀態轉為全膜潤滑狀態。當r0=70 mm<100 mm時處于混合潤滑狀態,接觸壓力較高;而當r0=130 mm>100 mm時處于全膜潤滑狀態,粗糙峰接觸壓力較低,如圖9(c)所示,總壓力與油膜壓力受r0的影響不大,且壓力峰向油膜出口區發生了偏移,見圖9(a)、(b)。

圖9 壓力隨綜合曲率半徑r0的變化趨勢
圖10(a)、(b)分別給出了混合潤滑條件下,油膜厚度和中層油膜溫度隨綜合曲率半徑r0的變化。由圖10(a)可見,隨著綜合曲率半徑r0的增加,中層油膜溫度降低,這是因為隨著綜合曲率半徑的增大,潤滑狀態轉為全膜潤滑狀態,粗糙峰壓力pa不斷減小,導致粗糙峰接觸的摩擦力減小,油膜中層溫度降低,使得潤滑油黏度增加。由圖10(b)可見,在混合潤滑條件下,隨著綜合曲率半徑的增加,油膜厚度增加,油膜頸縮現象越明顯。這是因為隨著綜合曲率半徑的增大,油膜中層溫度降低,使得潤滑油黏度增加,因此膜厚增加,這與膜厚比λ隨著綜合曲率半徑的增加而增加的結論一致(見圖8 )。

圖10 油膜溫度t、油膜厚度h隨綜合曲率半徑r0的變化
圖11表示平均摩擦因數fc、油膜最大溫度tmax隨r0的變化。可知,隨著r0的增加,tmax與fc均減小,這是因為隨著綜合曲率半徑的增大,粗糙峰接觸壓力不斷減小,使粗糙峰之間的摩擦力減小,雖然油膜溫度的降低使潤滑油的黏度增大而導致油膜內部摩擦力增大,但總的摩擦力是不斷降低的,又因載荷不變,故由公式(27)可知,fc減小。
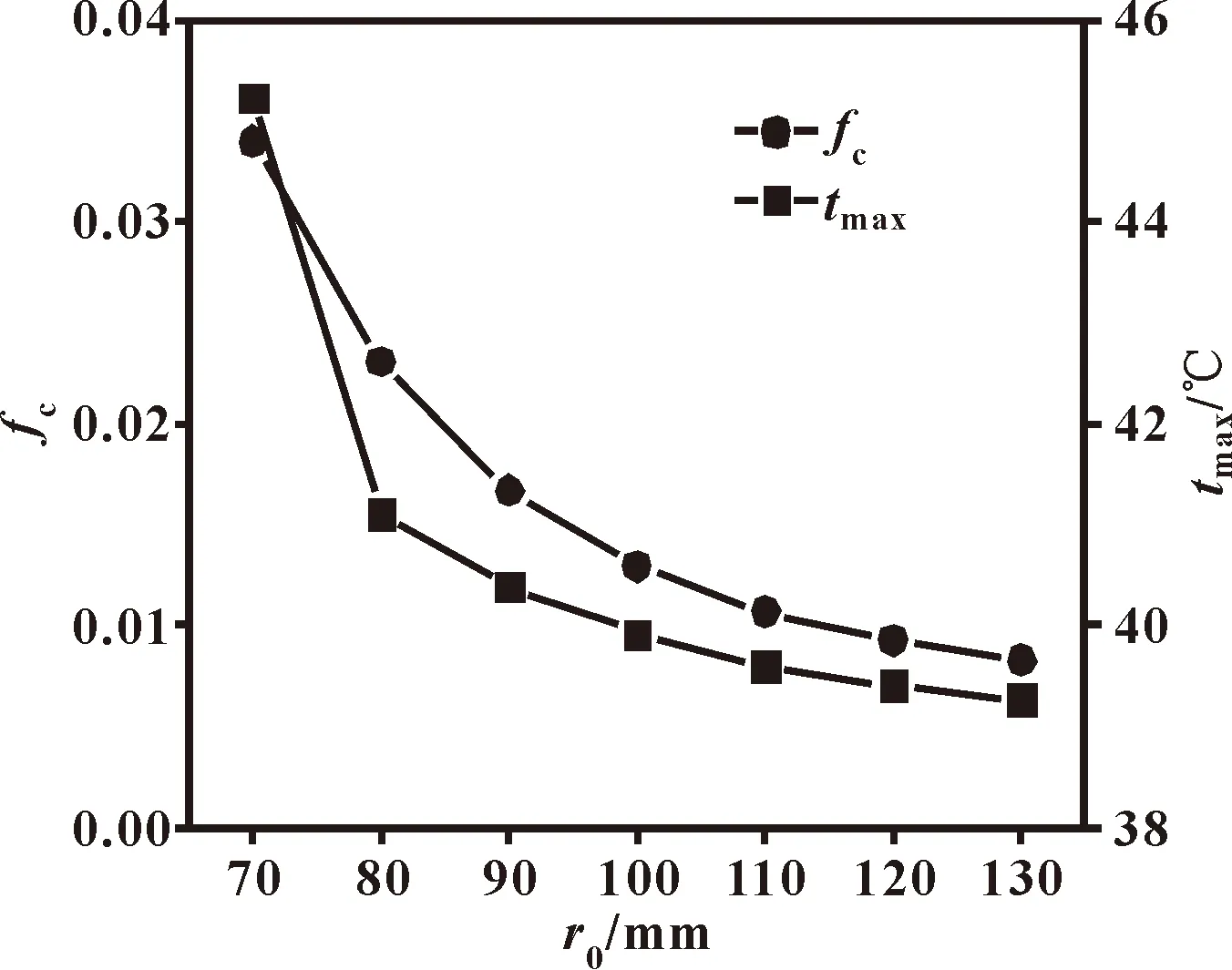
圖11 平均摩擦因數fc、油膜最大溫度tmax 隨綜合曲率半徑r0的變化趨勢
綜上所述,增大銷軸-鏈板副的綜合曲率半徑有利于改善其潤滑性能,但受銷軸、鏈板孔尺寸偏差的影響,導致綜合曲率半徑在一定范圍變化,因此,同一規格的齒形鏈在相同工況下,銷軸-鏈板副的潤滑性能存在一定差異。
4.3 表面粗糙度對潤滑特性的影響
為了分析銷軸鏈板孔表面的粗糙度對混合潤滑性能的影響,在綜合曲率半徑r0=100 mm、載荷參數W=5.19×10-6(pH=0.21 GPa)時,分析了表面粗糙度對膜厚比、最小膜厚、平均摩擦因數和最大油膜溫度的影響,如圖12所示。由圖12(a)可知,隨著表面粗糙度的增加,最小膜厚hmin增加,膜厚比λ不斷減小。當表面粗糙度較小時,表面粗糙度的變化對最小膜厚hmin的影響不大,但膜厚比λ呈現急劇減小的現象,這是因為在表面粗糙度較小時產生的動壓效應較小,最小膜厚增加的幅度小于表面粗糙度增加的幅度;當表面粗糙度增大至σ=0.4 μm時,接觸副由全膜潤滑狀態開始轉向混合潤滑狀態。

圖12 表面粗糙度σ對摩擦性能的影響
由圖12(b)可知,隨著表面粗糙度的增加,最大油膜溫度和平均摩擦因數均增加。這是因為隨著表面粗糙度的增加,粗糙峰接觸壓力不斷增大,使粗糙峰之間的摩擦增大,產生較多的摩擦熱,導致油膜溫度升高。當σ>0.4 μm時,平均摩擦因數與最大油膜溫度明顯增加,這是由于當表面粗糙度σ=0.4 μm時,潤滑狀態開始轉為混合潤滑所致。
圖13進一步給出了不同表面粗糙度σ下,總壓力pt、油膜壓力ph和粗糙峰接觸壓力pa的分布。可見,隨著表面粗糙度的增加,總壓力與油膜壓力減小,粗糙峰接觸壓力增加。原因在于,隨著表面粗糙度的增加,有更多的表面粗糙峰接觸,粗糙峰承擔更多的載荷,導致粗糙峰接觸壓力變大,油膜壓力變小。

圖13 壓力隨表面粗糙度σ的變化
4.4 載荷對潤滑特性的影響
圖14給出了在表面粗糙度σ=0.4 μm、綜合曲率半徑r0=100 mm時,膜厚比λ隨載荷的變化趨勢。可知,隨著載荷的增加,膜厚比不斷減小。根據膜厚比對潤滑狀態的影響,當1<λ<2.5時處于混合潤滑狀態,當λ>2.5時接觸區處于全膜潤滑狀態,可知對應載荷W=3×10-6~7×10-6時,接觸副處于混合潤滑狀態。

圖14 膜厚比λ隨載荷的變化趨勢
圖15表示平均摩擦因數fc、油膜最大溫升tmax隨載荷的變化趨勢。如圖所示,隨著載荷的增加,平均摩擦因數增大,油膜最大溫升不斷升高。這是因為隨著載荷的增加,粗糙峰接觸壓力不斷增大,使粗糙峰之間的摩擦力增大,產生較多的摩擦熱,導致油膜溫度升高。
在混合潤滑狀態下,總壓力pt、油膜壓力ph、粗糙峰接觸壓力pa隨載荷增加的變化如圖16所示。可見,隨著載荷的增加,油膜壓力ph、粗糙峰接觸壓力pa和總壓力pt均增加。
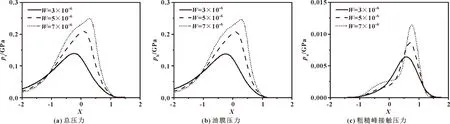
圖16 不同載荷下的壓力分布
圖17給出了不同載荷下,油膜厚度與中層油膜溫度的分布。由圖17(a)可見,隨著載荷的增加,油膜厚度不斷減小。這是因為載荷增加,使得在接觸區有更多的粗糙峰參與接觸,產生更多的摩擦熱,使油膜溫度升高,且油膜出口處溫升要大于油膜入口處溫升,這是由于粗糙峰的二次壓力峰引起的(見圖16(c))。溫度升高使得潤滑油黏度降低,導致油膜變薄,這也是銷軸-鏈板副出現磨損失效的原因之一。

圖17 不同載荷下膜厚h與中層油膜溫度t的分布
5 結論
(1)在混合潤滑條件下,隨著綜合曲率半徑的增加,油膜厚度增加,油膜溫度降低,可有效地改善銷軸-鏈板副的潤滑性能。但由于綜合曲率半徑受銷軸與鏈板孔徑尺寸偏差的不確定性影響,即使同一型號的齒形鏈在相同工況下,銷軸-鏈板副的潤滑性能也存在一定的差異。
(2)在混合潤滑條件下,隨著表面粗糙度或載荷的增加,油膜變薄,膜厚比減小,粗糙峰接觸壓力增大,油膜溫度也增大,潤滑狀態由全膜潤滑轉變為混合潤滑,增加了銷軸-鏈板副的磨損風險。

