橋梁基樁聲波透射法三維層析成像的空間插值技術研究

胡德輝

(佛山市公路橋梁工程監測站有限公司,廣東 佛山 528000)

1 橋梁基樁聲波透射法檢測技術概述

基樁檢測技術規范中要求采用聲波透射法檢測基樁質量時,樁徑大于或等于2 500 mm需要在內部埋設不少于4根聲測管,樁徑大于1 600 mm小于2 500 mm的基樁內部需要埋設4根聲測管,樁徑介于1 000 mm與1 600 mm之間的需要埋設3根,樁徑小于等于1 000 mm的基樁內部需要埋設不少于2根聲測管。實際工程中由于樁徑和成本的限制,單樁一般埋設2～3根聲測管,檢測1～3個剖面的混凝土波速分布,大直徑的橋梁樁等重要樁基礎最多埋設4根聲測管,得到6個剖面的混凝土波速分布[1]。

基樁檢測技術規范中要求超聲波發射和接受換能器的諧振頻率為30～60 kHz,混凝土的超聲波波速一般為4 500 m/s,則檢測用超聲波在混凝土中的波長約為7～15 cm,所以利用超聲波探測缺陷的尺寸范圍在分米級別。規范中要求兩根聲測線之間距離不大于25 cm。以兩根聲測線之間距離10 cm為例,取一對聲測管檢測混凝土剖面的寬度為10 cm,則基樁內部埋設兩根聲測管時,聲測管檢測混凝土剖面約占基樁橫截面的15%,基樁內部埋設三根聲測管時,聲測管檢測混凝土剖面約占基樁橫截面的30%,基樁內部埋設四根聲測管時,聲測管檢測混凝土剖面約占基樁橫截面的50%。即使埋設四根聲測管,使用聲波透射法檢測的范圍仍只有基樁橫截面的一半,如果埋設五根聲測管,檢測面積比會有所增大,但需要檢測9對聲測管的測面,工作量十分巨大。

傳統聲波透射法的結果分析采用概率法等結合工程經驗,得到聲學參數異常的聲測線,從而判斷缺陷出現的大致深度和類型,即使使用混凝土層析成像技術也只能得到占據基樁橫截面部分面積的混凝土剖面的波速分布,依舊不能完整反映出基樁內部缺陷的形狀大小和位置,不利于為下一步樁基礎承載能力評估和維護加固提供精確的數據。因此,相關單位有必要在多個二維超聲波層析成像剖面的基礎上,使用空間插值法計算得到剖面外離散單元的波速,從而獲得基樁整體詳細精確的質量情況。

2 空間插值技術分析

2.1 全局多項式插值法

全局多項式插值法通過將樣本點的測量值擬合成一個連續光滑的面,反映觀測區整體的變化趨勢,也稱趨勢面插值法。全局多項式插值法通過擬合而成的多項式方程生成反映變化趨勢的曲面,其特點是能通過趨勢面直觀的看出全局的趨勢,但由于多項式生成的曲面變化較為緩慢,面對變化劇烈的空間結構時擬合效果會差強人意,同時難以適應突變點尤其是位于邊界附近的突變點的影響,這些突變點極易給趨勢面帶來較大的擾動[2]。

2.2 三角測量插值法

三角測量插值法起源于三角定位法,又叫重心坐標插值法,首先將所有相鄰的三個樣本點兩兩相連構成一個三角形平面,保證三角形平面內部不包含任意樣本點,此時在坐標-值的三維空間中構成了一個傾斜的三角形,而整個觀測區域變成該三維空間中由多個三角形構成的多面體。三角測量插值法原理簡單,計算方便,但只能使用三個樣本點的測量值對未知點進行預測,無法靈活調整參考樣本點的數量,剩余樣本點全部被浪費,相比于其他方法,對未知點的預測效果較差。

2.3 反距離加權插值法

反距離加權插值法認為樣本點對未知點的影響與二者的距離相關,樣本點對未知點影響權重與二者之間的距離呈逆相關關系,因此被稱為“反距離加權”。樣本點在空間中的局部分布特征對反距離加權插值法的影響較大,反距離加權插值法適用于對樣本點數量多、分布均勻的空間數據[3]。

2.4 樣條插值法

樣條插值法的目的是計算得到一個通過所有樣本點同時曲率最小的光滑曲面,從而對未知點進行預測。樣條插值法理論上可以利用高次多項式來得到高階平滑的曲面,但實際中一般使用一階、二階、三階的低階多項式,其中三階樣條插值法最為常用。樣條插值法由于建立在獲得平滑曲面的基礎上,所以適用于變化緩慢的空間結構,例如氣溫、污染物濃度、信號強度等,對樣本點密度大、數量多的空間數據會有較好的插值效果,對于變化劇烈的空間結構,應用時要謹慎考慮[4]。

2.5 克里金插值法

克里金法基于變異函數理論,能夠在有限區域內的變量進行線性無偏最優估計,能較好地處理空間的隨機性,被廣泛應用在地質、氣象、信號、土壤等領域。

線性克里金插值法的目的在于求出權重系數λi(i=1,2,3……n),使得Z(x0)成為搜索區域內Z(x)最優無偏估計量。線性克里金插值法的回歸模型公式如下

普通克里金插值法假設區域化變量Z(x)在區域空間V中的數學期望存在但為未知常數,其無偏性條件為E[Z(x0)]=E[Z(x)],即

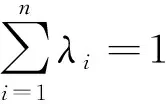
之后需要在滿足無偏性條件下,求得使估計方差值最小的權重系數λi(i=1,2,3……n),該過程一般使用拉格朗日乘數法,最終普通克里金插值法的計算步驟如下。

(1)選取合適的臨近點搜索模式,計算待預測的未知點x0周圍臨近點兩兩之間的半方差,其中n為距離為h的臨近點點對數量,得到離散半方差函數

(2)選取合適的變異函數模型,將離散半方差函數擬合為變異函數λ(h)。

(3)計算臨近點兩兩之間的半方差矩陣Γ,未知點x0和其臨近點兩兩之間的半方差向量Γ0,求解矩陣方程得到權重系數λi(i=1,2,3……n)。

(4)將權重系數λi(i=1,2,3……n)代入回歸模型公式中,求得未知點λ0的預測值。

3 克里金插值法改進

3.1 克里金空間插值法在基樁聲波透射成像中存在的缺陷分析

混凝土波速層析成像效果示意圖如圖1所示。該混凝土中心紅色框體區域為低強度的缺陷區,在混凝土波速界面中被設置低速異常區域,該區域混凝土波速設定為3 200 m/s,紅色框體外的區域是正常質量區域,在混凝土波速界面中被設置正常波速區域,該區域混凝土波速設定為4 000 m/s。從圖1中可以看出,混凝土波速層析成像能夠明確反映出界面上的波速分布,確定混凝土波速低速異常區域的位置和大小,同時在成像結果中能夠看出界面上的波速分布存在著一定規律,即從射線入射點經過低速異常區域再到射線接收點,網格單元的波速逐漸降低再增加。這證明了當質量正常的混凝土中存在低強度的缺陷區域時,這樣的混凝土的層析成像結果確實存在一定的空間結構性,為使用克里金插值法提供了基礎。

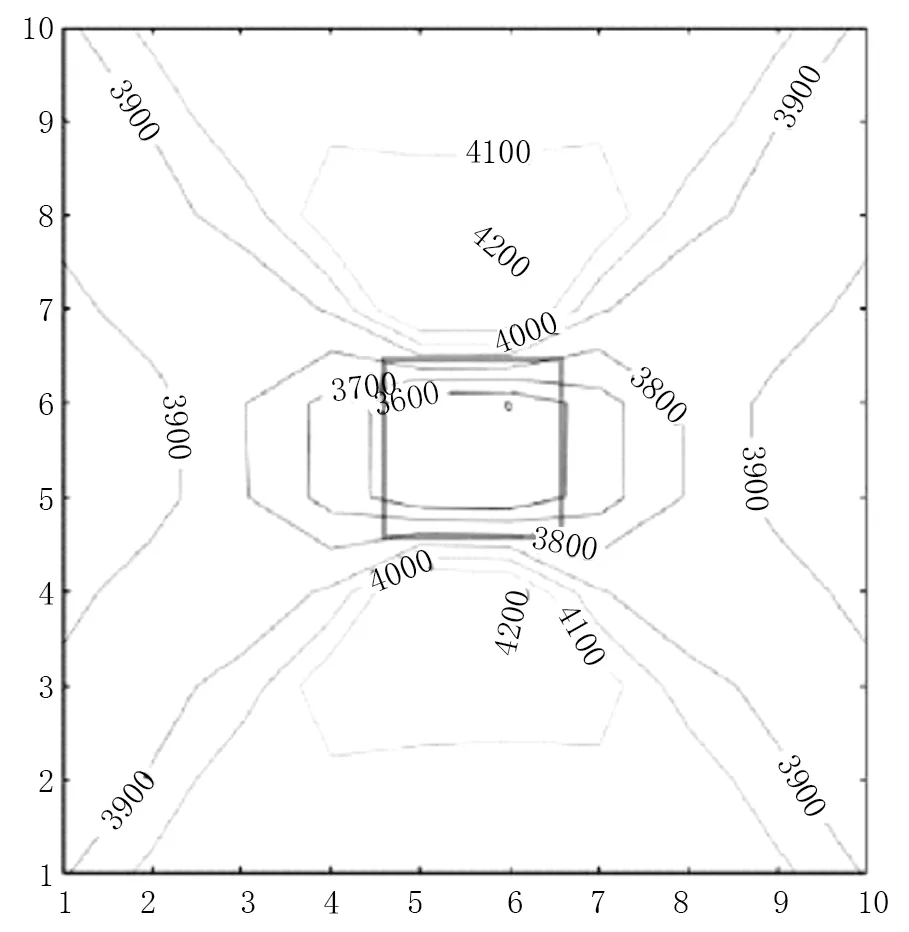
圖1 混凝土波速層析成像效果示意圖

混凝土灌注樁常出現的缺陷問題包括:樁底沉渣過厚、斷樁、夾泥和縮徑。樁底沉渣過厚和斷樁可通過低應變法和聲波透射法快速、準確的發現并確定,同時其對樁基礎承載能力的影響也較為明確。夾泥是由施工流程不規范和復雜地層共同影響造成,縮徑的原因一般是由于泥漿護壁塑性土膨脹導致孔徑縮小,夾泥和縮徑在基樁質量檢測過程中的共同點是發生的位置一般位于樁身的四周,基樁中心極少出現,這一特點有利于聲波透射法對這兩種缺陷位置的確定,但聲波透視法無法確定這兩種缺陷的具體信息,例如三維尺寸、缺陷區域樁體的質量等等,所以依舊需要基樁三維層析技術檢測夾泥和縮徑這兩種缺陷的信息。

基樁缺陷成像空間插值的樣本點來源于通過聲測管采用層析成像得到的聲測管連線沿深度方向剖面的樁身混凝土波速分布,該樣本點的采樣方法決定了基樁缺陷成像空間插值的特點。該基樁中埋設了4根聲測管,每對聲測管連線沿深度方向的剖面離散為10×10的網格進行層次成像,因此在基樁橫截面中形成以四根聲測管為頂點的10×10的網格,并認為網格中每個單元內的波速均勻分布并保持一致。借助4根聲測管兩兩進行測量并通過層次成像計算而得到6個沿深度方向的剖面的混凝土波速作為樣本點單元在基樁橫截面上呈正方形框體型和“X”型分布,需要進行波速空間插值的未知點單元集中分布于基樁橫截面上網格的中心,樣本點和未知點均按一定規律集中分布,極其不均勻。并且夾泥和縮徑這類缺陷不是在基樁橫截面中隨機存在,而是出現在基樁橫截面四周的概率比較大,這就導致基樁橫截面的波速分布大部分區域是平緩的波速正常區域,邊界這類特定位置可能存在具有空間結構性的低速異常區域。基樁橫截面上樣本點和未知點的分布特征和整體的空間結構性給克里金插值法鄰近點搜索方式的確定增加了困難,因此也就導致了由離散半方差函數擬合變異函數的精度降低。

克里金插值法的臨近點搜索有兩種模式,一是固定搜索數量,搜索并選取距離待預測未知點最近的n個樣本點,二是固定搜索距離,搜索并選取距離待預測未知點d以內所有樣本點。由于前文所訴的基樁橫截面上樣本點和未知點的分布特點,選擇固定搜索點數模式時,會出現最大搜索距離下搜索出多個樣本點,超出固定的搜索數量,無法在相同距離下從多個樣本點中選擇出滿足搜索數量和空間分布的有限樣本點。所以克里金插值法應用于基樁缺陷成像空間插值時采用固定搜索距離更為合適。

使用克里金插值法臨近點搜索距離確定為2倍網格單元邊長時,在克里金插值法應用于基樁缺陷成像空間插值時,使用常用的球狀模型等或是不常用的空洞效應模型這些已知的半方差模型,對未知點構造的離散半方差函數進行擬合會十分困難,均會產生較大的殘差,同時相關系數R2會更加接近0,無法擬合出精度較高的變異函數,從而導致最終的預測結果出現較大的誤差。

3.2 克里金空間插值法優化方法

基于上述提出的克里金空間插值法缺陷,本文對該方法的搜索模式進行了改進,提出一種針對基樁缺陷成像空間插值的區域化搜索克里金插值法。

區域化搜索克里金插值法在選取臨近點搜索模式時,放棄了傳統的固定搜索數量模式和固定搜索距離模式,而是根據前文所訴的基樁橫截面上樣本點和未知點的分布特點,將基樁橫截面的網格空間按照對稱的方式劃分為8個搜索區域,每個搜索區域內的樣本點共同構成該區域內未知點的臨近點空間,即該區域內所有未知點預測均以該臨近點空間構成的離散半方差函數的計算基礎。

該改進方法的優點在于考慮到了基樁橫截面上樣本點和未知點分布的集中性和對稱性,每個搜索區域內的樣本點和未知點的分布特征相同且固定,樣本點分布在三角形搜索區域的斜邊和外直角邊上,未知點分布在三角形搜索區域的中心,因為夾泥和縮頸導致的缺陷區域多分布于基樁橫截面四周,外直角邊上的樣本點可以較好反映缺陷的信息,而斜邊上的樣本點可以較好反映缺陷深入基樁內部程度的信息,該臨近點搜索模式綜合考慮了臨近點搜索的效率和對空間結構性的反映。

傳統克里金插值法將離散半方差函數擬合成離散函數的目的在于傳統克里金插值法需要找到一個反映任意距離下兩點之間空間結構關系的函數,而離散半方差函數只包括有限個距離的點對的空間結構關系,無法適用于后續確定待預測未知點與鄰近點之間的空間結構關系。而在該改進方法的臨近點搜索模式下,在一個搜索區域中,任意未知點到任意臨近點的距離均屬于該搜索區域中臨近點構成的離散半方差函數中的自變量,因此可以直接使用該搜索區域中臨近點構成的離散半方差函數確定該搜索區域中任意未知點與任意臨近點的空間結構關系,省去了離散半方差函數按照半方差模型擬合變異函數的步驟,該步驟中帶來的誤差直接消失,從而提高了最終的插值精度。

4 結 論

綜上所述,本文提出了一種針對基樁缺陷成像空間插值的區域化搜索克里金插值法,將基樁橫截面的網格空間按照對稱的方式劃分為8個搜索區域,每個搜索區域內的樣本點共同構成該區域內未知點的臨近點空間,假設每個搜索區域內的樣本點和未知點的分布特征相同且固定,則可以直接使用離散半方差函數確定任意未知點與任意臨近點的值的半方差,簡化了擬合變異函數的過程,從而提高克里金插值法的預測精度。