同一種思維方式“待”出不一樣的人生
——用待定系數法處理有通項的數列放縮問題
汪本旺
(浙江省湖州市安吉縣孝豐高級中學)
放縮法證明數列不等式歷來是高考數學的難點,在高考數列試題中經常扮演拉開差距的角色.由于放縮法靈活多變,技巧性要求較高,所謂“放大一點點則太大,縮小一點點則太小”,這就讓許多學生很茫然,找不到頭緒,摸不著規律,覺得高不可攀.如何找到放縮的“橋梁”,如何把握放縮的度,使得放縮“恰到好處”,是力求一步到位就能完成問題證明的關鍵.本文對三種類型的數列,用同一種思維——待定系數,巧妙地解決適度放縮問題.
一、問題背景
在2020年11月浙江省湖州市期末第一次聯考考試中,出現一題數列解答題,題目如下(節選):
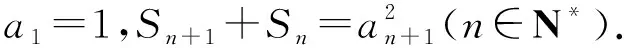
(Ⅰ)求a2,a3的值,并寫出數列{an}的通項公式;
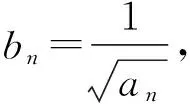
該題第(Ⅱ)問最終統計結果基本全軍覆沒,課后通過調查發現大部分學生花了很多時間但最終還是未能解決該題,本文先給出第(Ⅱ)問的官方解析:
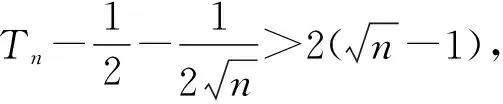
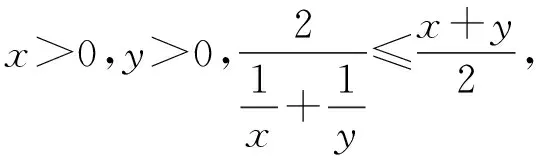
通過目標值或目標式的分析常常能得到放縮的路徑.本文就近年來高考中常考的三種有通項的數列不等式問題,談談粗淺的思考.
二、基本類型
1.分母為二次函數型
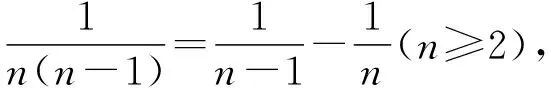
1.1 案例分析
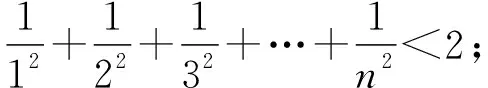
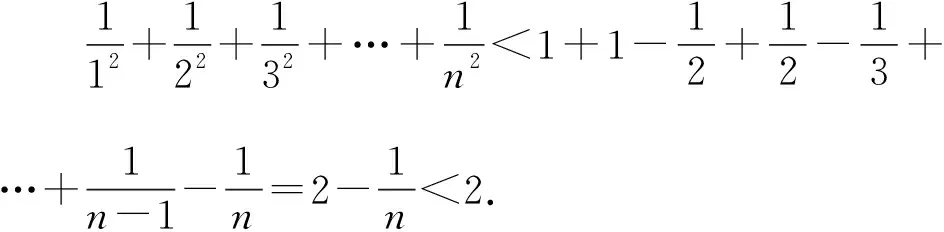
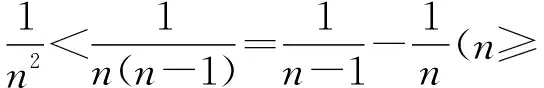
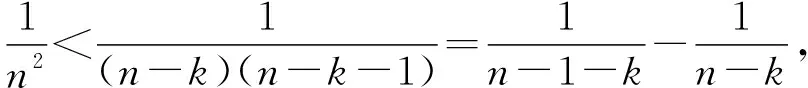
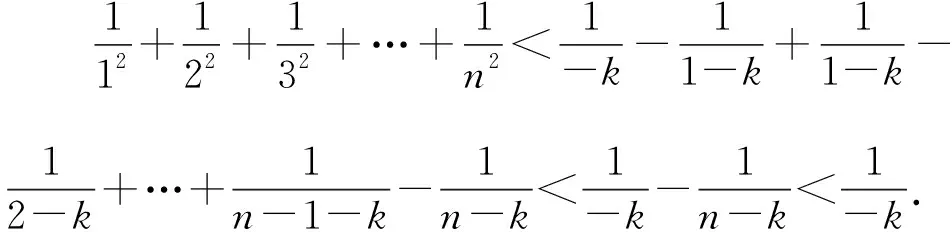
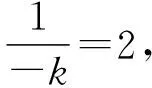
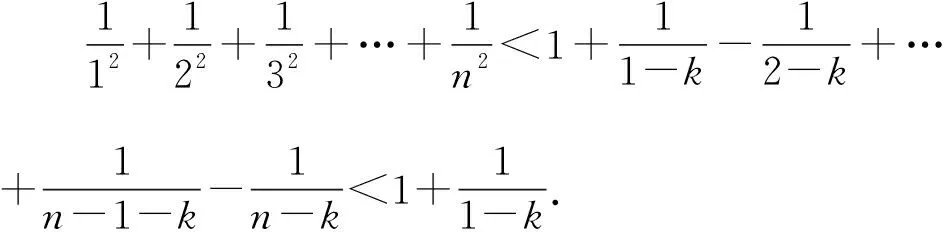
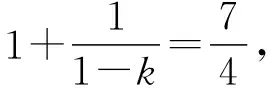
1.2 思維策略
1.2.2 目標值指引
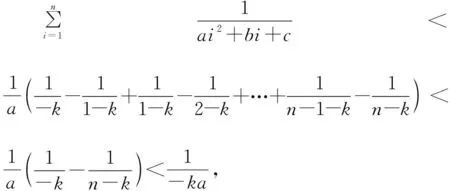
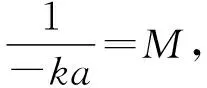
1.2.3 驗證不等式
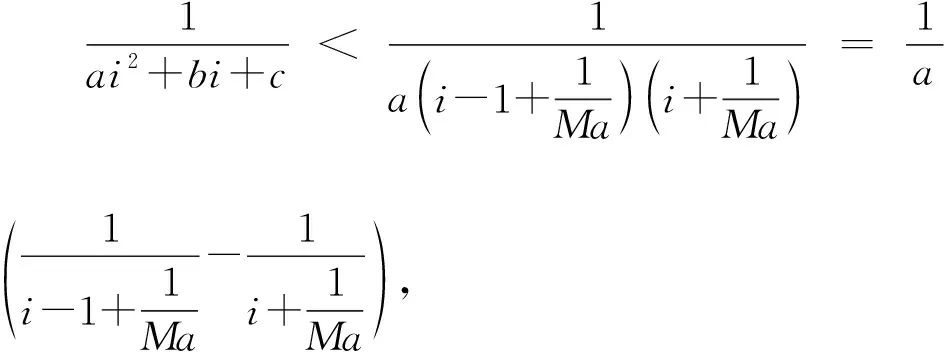
1.3 知識運用
(b)I borrowed the book from the libraryI can keep for a week.
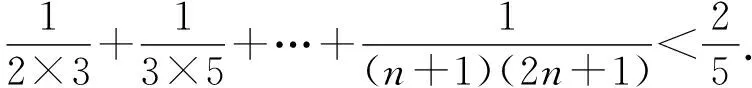
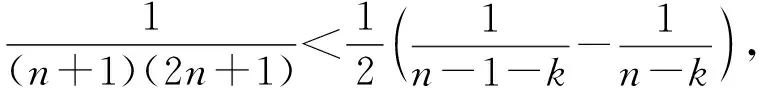
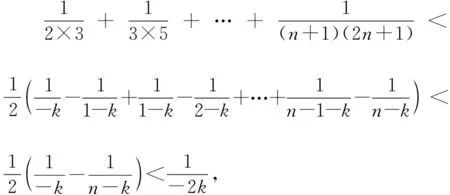

即證8(n+1)(2n+1)>(4n+1)(4n+5),
即證8n+5>0,該不等式顯然成立,命題得證.
【點評】普通學生初次接觸此類題,是很難做到精準放縮的.本文所述的“待定系數法”,突破了此類問題學生找不到思路的瓶頸.而更一般的放縮“通項公式”(*),引導學生將一項分裂為兩項,而且此兩項必為同一新數列的連續兩項,從而為后續的消項作好了準備.這對于學生深刻理解數列裂項求和的本質是非常有幫助的.
2.分母為指數型
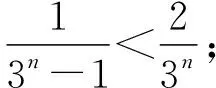
2.1 案例分析
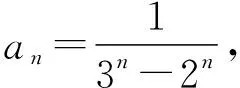
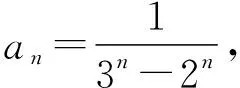
對于例2,可以嘗試上述所講的方法解決,但是能否有一種本質的方法一次性解決這兩個問題呢?由于通項為指數型,而指數型又與等比數列有密切聯系,那么是否可以嘗試放縮到等比數列呢?為了控制放縮的精度,引入待定正系數k,即構造如下放縮“通項公式”:
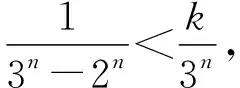
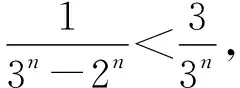
事實上,當n=1時,2n-1=3n-1,當n≥2時,2n-1<3n-1.
那么,對(Ⅰ)的證明可以稍作調整,如下:
當n=1時,不等式恒成立;
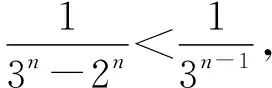
在(Ⅱ)中,作如下考慮,保留第一項,從第二項開始待定系數放縮,
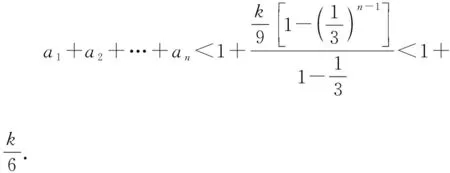
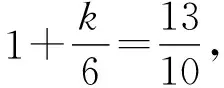
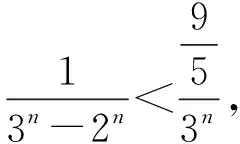
事實上,當n=2時,2n-2=3n-2,當n≥3時,2n-2<3n-2.
那么,對(Ⅱ)的證明可以稍作調整,
當n=1,2時,不等式恒成立;
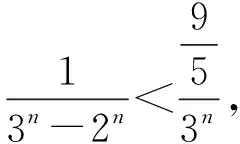
2.2 思維策略
2.2.1 算法式模式
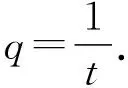
2.2.2 目標值指引
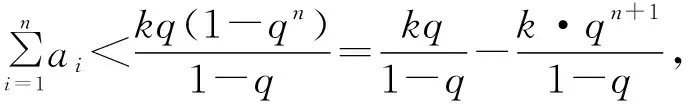
2.2.3 驗證不等式
把2.2.2中算出的k帶入不等式ai 2.3 知識運用 那么從第二項開始放縮: 證明:當n=1,2時,不等式顯然成立; 回歸問題背景,選擇調和不等式的確非常簡單,但是對學生來說,實在是技術含量較高,那么對于該類問題,能否找到一種直接明了,更加本質的方法呢? 3.1 案例分析 3.2 思維策略 3.2.1 算法式模式 3.2.2 目標值指引 3.2.3 驗證不等式 3.3 回歸背景 根據思維策略,對于問題背景中的問題,做如下分析: 證明:當n=1時,不等式恒成立; 在高中數學數列放縮問題上,巧妙的應用待定系數法優化解題思路,找到問題本質,將原本高不可攀的問題簡單化、程式化.在高中數學數列放縮問題教學中,有效地滲透此類方法,能夠有效地解決學生在解題中解題無思路、方法選用不當導致放大或放小、準確率低下等問題.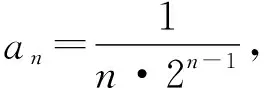
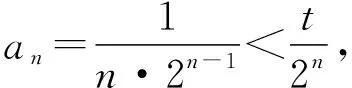
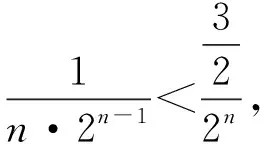
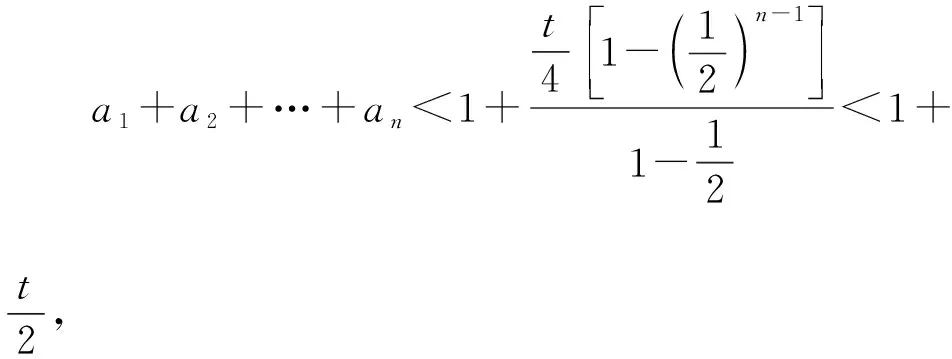
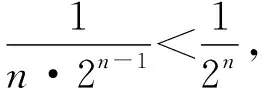
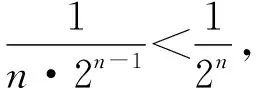
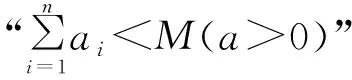
3.分母為根式型

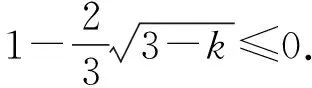
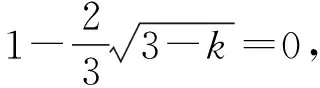

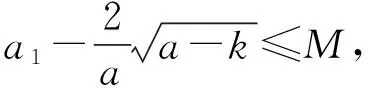
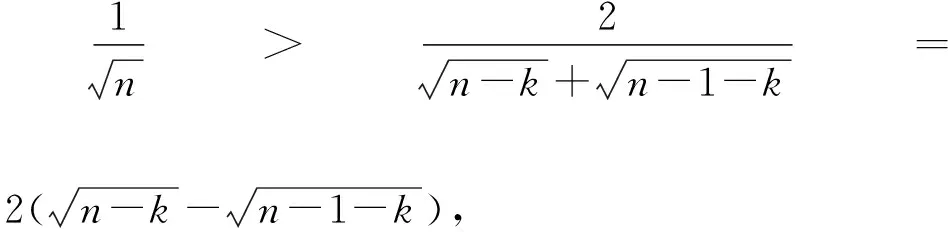
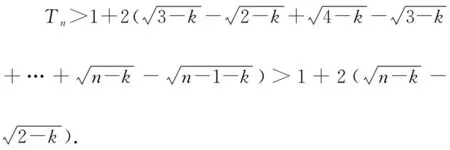
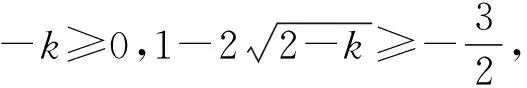

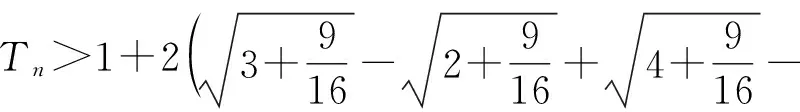
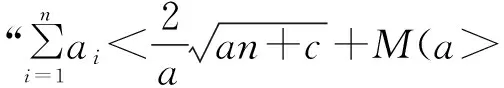
三、結束語


