平拋運動問題的歸類解法與技巧

胡道成

(貴州省畢節第三實驗高級中學)

平拋運動是一種重要的曲線運動,解決平拋運動問題是在“化曲為直”思想的指導下,將平拋運動分解為水平方向的勻速直線運動和豎直方向的自由落體運動,是“合成與分解法”這一重要物理方法的具體應用。平拋運動問題與生產生活和現代科技結合得非常緊密,能夠承載“情境問題”,內容還涉及牛頓運動定律及“等效思想”的應用,對考查學生的理解能力、推理論證能力、模型建構能力和“能量觀念”具有不可替代性,也就成了高考命題的熱點。做平拋運動的物體在運動過程中往往會受到幾何條件的約束,因此,解題策略上要按落點情況進行歸類,解題方法上要以“速度正交分解法或位移正交分解法”為突破口,解題技巧上要以求時間為橋梁,結合等時性、三角函數關系、勾股定理、相似三角形等知識來解決問題,形成結構化、程序化的知識結構體系至關重要。

一、物體落點在豎直面上,水平位移決定時間

【例1】如圖1所示,玩具射擊槍水平放置,槍與目標靶中心位于離地面足夠高的同一水平線上,槍口與目標靶之間的距離為x=100 m,子彈射出的水平速度v0=100 m/s,子彈從槍口射出的瞬間目標靶由靜止開始釋放,不計空氣阻力,重力加速度g=10 m/s2。

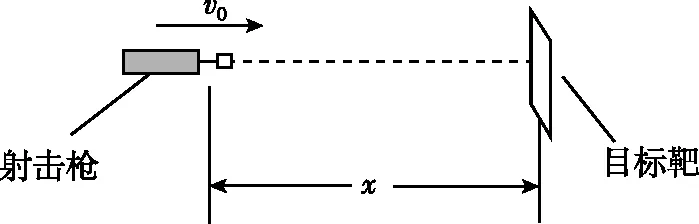
圖1

(1)求子彈從射出到擊中目標靶的時間t;

(2)求目標靶從釋放到被子彈擊中下落的高度h。

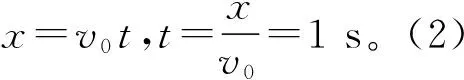
【點評】解題過程就是尋找等量關系的過程,本題中子彈恰好擊中目標靶,說明子彈和目標靶的運動時間上相等,空間上下落高度相等,據此列出等式即可求解。

二、物體落點在水平地面上,豎直位移決定時間

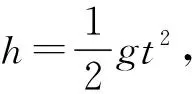
【例2】如圖2所示,x軸在水平地面上,y軸在豎直方向。圖中畫出了從y軸上不同位置沿x軸正向水平拋出的三個小球a、b和c的運動軌跡,小球a從(0,2L)拋出,落在(2L,0)處;小球b、c均從(0,L)拋出,分別落在(2L,0)和(L,0)處。不計空氣阻力,下列說法正確的是 ( )

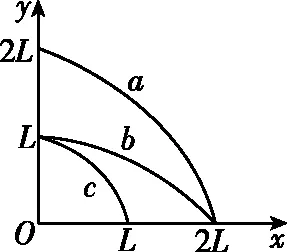
圖2

A.a和b的初速度相同

B.b和c的運動時間相同

C.b的初速度是c的2倍

D.a的運動時間是b的2倍

【答案】BC

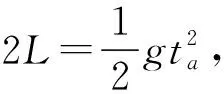
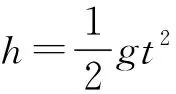
三、物體垂直打在斜面上,分解速度突破

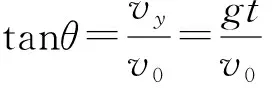
【例3】如圖3所示,長木板OA的傾角θ=30°,在O點正上方的P處水平拋出一個小球,結果小球恰好垂直打在板面上距離O點為L的B點。重力加速度大小為g,空氣阻力忽略不計。下列說法正確的是 ( )

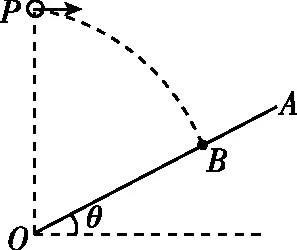
圖3

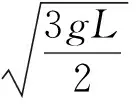
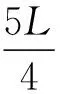
【答案】BD

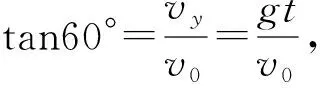
【點評】對于物體垂直打在斜面上的情形,分解末速度是解題突破口。本題未給出初速度,先由幾何關系找出小球水平位移和豎直位移,通過分解小球在B點的速度,根據幾何關系找出小球初速度與時間的關系即可求出時間,以此為橋梁又可求出小球打在B點的速度,再由幾何關系求出O、P兩點間的距離。

四、物體從斜面頂端拋出落到斜面上,分解位移突破

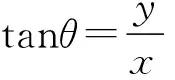
【例4】高山滑雪是2022年北京冬奧會的比賽項目之一。如圖4所示,假設兩名高山滑雪運動員a、b(均可視為質點)從雪道末端先后以初速度之比va∶vb=1∶3沿水平方向向左飛出,不計空氣阻力,兩名運動員從飛出至落到雪坡上的整個過程中,下列說法正確的是 ( )

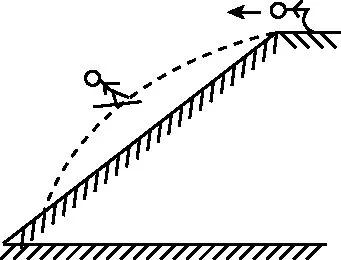
圖4

A.他們飛行的時間之比為3∶1

B.他們的水平位移之比為1∶3

C.他們落到雪坡上的瞬時速度方向不相同

D.他們在空中離雪坡的最大距離之比為1∶9

【答案】D

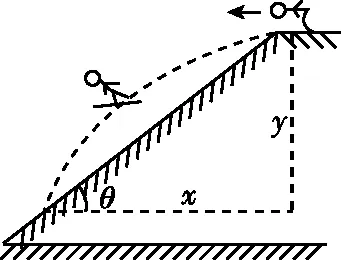
圖5

【點評】對于滑雪這類體育運動中的平拋運動問題,構建平拋運動模型往往是解決問題的基礎。本題中的運動員從雪坡上端水平飛出后落到雪坡上,識別出“斜面+平拋運動”模型后,通過分解位移就能找到求解時間的突破口,進而結合幾何關系和平拋運動規律進行解答;對于“求物體離斜面的最大距離”的問題,則用“物體垂直于斜面方向上的分速度為零時,物體離斜面的距離最大”來解決。

五、物體落點在曲面凹側或凸側,軌跡與曲面相切,通過“角度關系”來突破

物體落在曲面凹側或凸側,并與曲面相切的問題,解題的突破口在于充分利用末速度與曲面相切的特點,分解末速度,再用豎直速度求出運動時間,往往問題就能迎刃而解;對于末速度與曲面不相切的問題,則要用分解位移的方法來求解;對于物體平行于斜面方向進入斜面上的問題,也是根據瞬時速度方向與斜面方向平行的幾何關系,通過分解速度來進行求解。

【例5】如圖6所示,圓弧形凹槽固定在水平地面上,其中ABC是位于豎直平面內以O為圓心的一段圓弧,OA與豎直方向的夾角為α,一小球以速度v0從桌面邊緣P水平拋出,恰好從A點沿圓弧的切線方向進入凹槽。小球從P到A的運動時間為________,直線PA與豎直方向的夾角β為________。

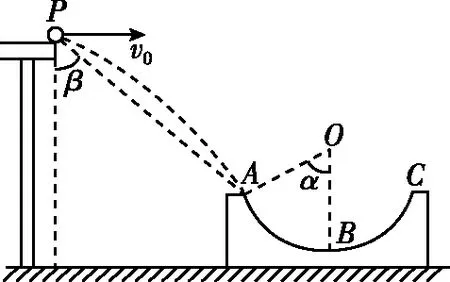
圖6

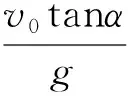
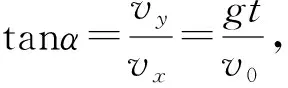
【點評】本題的解答過程中,抓住小球沿切線方向進入曲面這個條件,通過連接落點和圓心,由幾何關系找出分解速度所需的角度,利用三角函數關系求出運動時間,然后分解位移來尋找位移偏向角與速度偏向角之間的關系,從而使問題得以解決。對于小球做平拋運動與曲面不相切的問題,則需要分解位移,且落入曲面高度相同的情況下,可能會有兩個不同的水平位移,需要注意多解問題。

【例6】如圖7所示,ab為豎直平面內的半圓環acb的直徑,c為環上的最低點,環半徑為R。將一個小球從a點以初速度v0沿ab方向拋出,重力加速度為g,不計空氣阻力。則 ( )

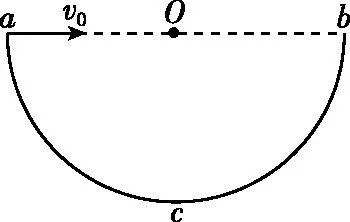
圖7

C.當小球的初速度v0取適當值時,小球可以垂直撞擊圓環

D.小球的初速度v0不同,撞擊到環上的運動時間可能相同

【答案】AD

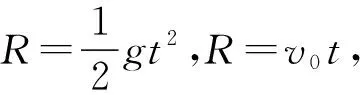
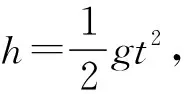
六、物體落在邊界范圍內的臨界問題,求時間突破

平拋運動的臨界問題主要是球類不觸網也不出界問題、小物體落入容器問題或穿越矩形孔問題之類的“受限”問題,解決問題的基本思路是將實際問題轉化為物理模型,利用平拋運動的軌跡,根據幾何關系尋找水平速度、豎直速度、水平位移、豎直位移等臨界條件,結合平拋運動的分解方法和基本規律進行求解。

【例7】乒乓球發球機是一個很好的輔助練習者練球的工具。如圖8所示的乒乓球桌面ABCD的AB邊長為L1,BC邊長為L2,球網GIJK豎直放置于桌面的正中間,網高為h;發球機簡化為EF,其中E點固定在AB邊的中點,F點為乒乓球發射點,EF始終保持豎直,高度為H(可調)。乒乓球看成質點,每次均從F點水平發射,發射方向可以在水平面內任意調整,不計空氣阻力和周圍環境對乒乓球運動的影響,也不考慮乒乓球旋轉,當球擦網而過時,則下列說法正確的是 ( )

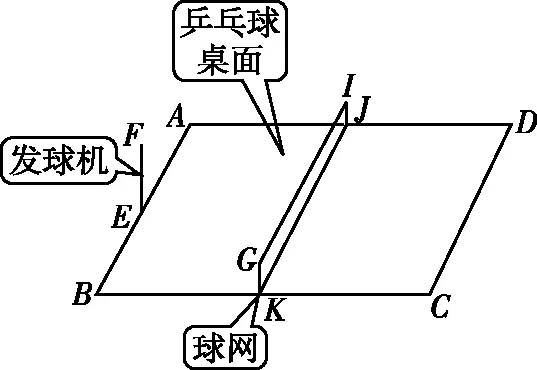
圖8

C.只要H大于h,就一定能設置合適的發球速率,使球落在JKCD區域內

D.若球以垂直于AB邊的方向發射能夠擦網而過后直接落到CD邊界上,則適當調整發射速度后,只要是落在CD邊界上的球一定是擦網而過的

【答案】D

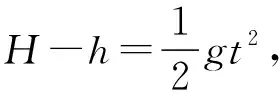
【點評】由于高度決定了時間,水平位移由初速度和高度決定,因而乒乓球可能會出現恰好過網或恰好不出界的臨界狀態。解決這類問題的關鍵是確定臨界狀態：一是發球速率較小時,乒乓球剛好沿中心線擦著球網上邊緣而落到球網右側桌面上;二是發球速率較大時,乒乓球剛能落在球網右側桌面上,且落點在桌角處。處理這類臨界問題需要認真觀察具體情境,充分發揮空間想象能力,學會換個視角看情境(側視、俯視),順利識別出情境中的物理模型至關重要。

七、物體落在圓盤上的組合問題,求時間突破

做平拋運動的物體落在做圓周運動的物體上這類組合問題,需要利用豎直位移決定時間,求出時間作為解題的紐帶,將水平位移與落點的半徑聯系起來,要注意的是圓周運動的周期性運動可能會導致出現多解。

【例8】如圖9所示,M是水平放置的半徑足夠大的圓盤,繞過其上表面圓心的豎直軸OO′勻速轉動,以經過圓心O水平向右的方向作為x軸的正方向。在O正上方距盤面h處有一個正在間斷滴水的容器,該容器從t=0時刻開始隨傳送帶沿與x軸平行的方向做勻速直線運動,速度大小為v。已知容器在t=0時滴下第一滴水,以后每當前一滴水剛好落到盤面上時再滴一滴水。

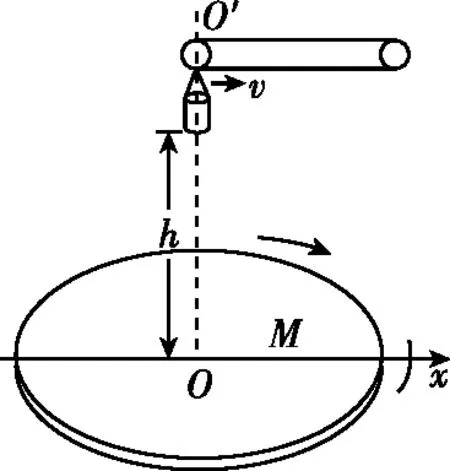
圖9

(1)每一滴水經過多長時間落到盤面上;

(2)要使每一滴水在盤面上的落點都位于一條直線上,求圓盤轉動的最小角速度ω;

(3)求第二滴水與第三滴水在盤面上的落點間的最大距離s。

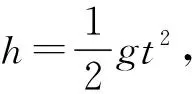
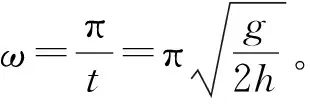
【點評】對于平拋運動與圓周運動的組合問題,解題突破口都是用時間作為橋梁,需要用“側視”和“俯視”來觀察兩個運動過程的具體情景,注意周期性導致的多解,尤其要弄清待求量是圓盤轉過nπ還是2nπ的情形,還要確定n的取值范圍;若涉及極值問題,則尋找極值條件是個難點,要善于畫出示意圖來分析。

八、物體落在“函數面”上,用曲線方程突破

平拋運動物體與圓面、橢圓面、拋物面等的“邂逅”問題,拋體運動的落點位置必然與這些曲面對應的函數產生聯系,落點的位置坐標一定滿足對應的曲線方程,且落點與拋出點之間的水平和豎直位移又滿足平拋運動基本規律,實現了物理規律與曲線方程、數學方法的完美組合。

【例9】如圖10所示,一個質量為0.4 kg的小物塊(可視為質點)以v0=1 m/s的初速度從水平臺上的O點水平飛出,擊中平臺右下側擋板上的P點。現以O為原點在豎直面內建立如圖所示的平面直角坐標系,擋板的形狀符合方程y=x2-6(單位：m)的曲線,不計一切摩擦和空氣阻力,重力加速度g=10 m/s2,則下列說法正確的是 ( )

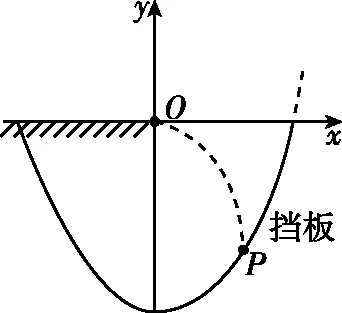
圖10

A.小物塊從O點運動到P點的時間為1 s

B.小物塊剛到P點時瞬時速度方向與水平方向夾角的正切值等于5

C.小物塊剛到P點時速度大小為10 m/s

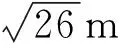
【答案】AD

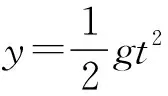
【點評】處理平拋運動物體與圓面、橢圓面、拋物面等“函數面”結合的問題,抓住拋體運動的落點位置坐標一定滿足對應的曲線方程,且拋體(質點)的運動過程也滿足平拋運動基本規律,結合起來就能找到解決問題的方法。值得一提的是有些問題里的“拋出點”與函數方程的“原點”并不重合,這時還要將落點的位置坐標進行適當變換才滿足曲線方程,代入數據計算時要倍加小心。