優質創新試題選登

1.2022年2月10日,日本花滑選手羽生結弦在第24屆北京冬奧會上挑戰4A遺憾失敗。4A全稱為阿克塞爾四周跳,是花樣滑冰所有跳躍動作中難度系數最高的,運動員需要在空中旋轉四周半,如圖1。如圖2,一花滑運動員跳起后離地高度可達0.8 m,落地屈膝的豎直作用距離為0.2 m,作用時間為0.1 s。已知該名運動員的體重是53 kg,重力加速度g取10 m/s2。則落地過程,該名運動員受到地面垂直方向的平均作用力約為其體重的 ( )

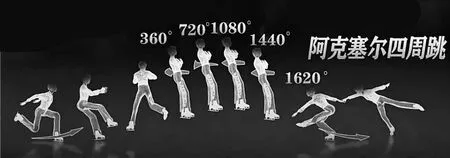
圖1

圖2

A.2倍 B.3倍 C.5倍 D.7倍

【試題分析】本題與生活緊密聯系,主要考查學生模型建構能力。符合四翼中應用性的要求。以運動員的重心作為研究對象,利用自由落體運動規律求得運動員落地瞬間的速度。通過合理假設,落地屈膝可看作勻減速運動求得作用時間,通過動量定理求出這段時間地面對運動員的作用力。

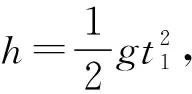
【解析二】由動量守恒定律得Ft-mg(t+t1)=0,解得F=5mg。

【答案】C

(作者姓名、單位：江賢聰 廣州市第五中學)

2.2022年春晚舞臺上的歌曲《時代感》唱出了對祖國日新月異發展的自豪和對未來的憧憬。在演唱的過程中,演員活力四射、跳出畫面的情景給我們留下了很深的印象。如圖3,關于演員雙腳剛要離開地面的過程中,不計空氣阻力,下列說法正確的是 ( )

圖3

A.地面對演員的支持力的沖量不為零,做功也不為零

B.演員的機械能守恒

C.演員處于超重狀態,且加速度的方向與其動量改變量的方向相同

D.地面對演員的支持力大于演員對地面的壓力

【試題分析】試題以春晚舞臺上的歌曲《時代感》為試題底色,激發學生熱愛祖國的情感、提升他們的民族自信心和自豪感。用演員在表演中跳離地面的過程為情境,考查學生由“實際問題”構建“物理模型”的能力及學生對牛頓運動定律、機械能守恒定律、動量定理、沖量以及功的理解;試題要求學生結合題目信息,考慮演員跳離地面的過程,應用質點模型對本題進行求解。試題突出物理學科的基礎性,既注重對核心物理概念和規律的考查,也注重對探究過程、研究方法等內容的考查,試題情境與內容的有機融合,考查學生靈活運用所形成的物理觀念、科學思維分析解決實際問題的能力,落實物理學科核心素養的培養。引導學生注重基礎,促進課堂回歸教材。

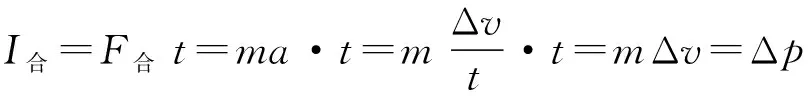
【答案】C

(作者姓名、單位：李曉青 邯鄲市第十中學)

3.斯諾克(Snooker)是臺球比賽的一種,如圖4,5,斯諾克臺球有時也被稱為障礙臺球。此項運動擊球次序為一個紅球、一個彩球直至紅球全部落袋,然后按彩球分值由低至高的順序也至全部離臺為止,最后以得分高者為勝,所有球的重量必須相同。在水平桌面上,對質量為m的白球以速度v0擊打一靜止的紅球的四個全過程進行了頻閃照相拍攝,如圖所示,據此可推斷,在誤差范圍內,以下說法正確的是 ( )

圖4

圖5

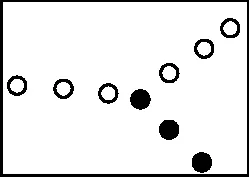
甲

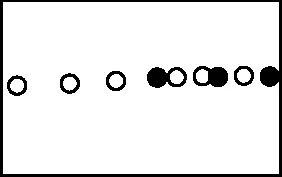
乙

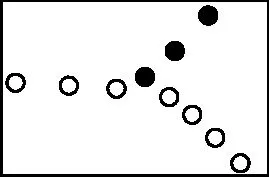
丙

丁

A.甲中系統動量不守恒

B.乙中系統機械能守恒

C.丙中系統損失的動能少于碰撞前總動能的50%

D.丁中對白球而言,碰撞前后受到的沖量大小為2mv0

【試題分析】本題考查動量守恒定律。要求學生基本概念要過關,落實物理觀念素養的培養,還需要能將情景與模型相結合,對其科學思維的考查要求較高,還要結合數學估算進行分析與處理,回憶相關的實驗情景,對動量相關知識點考查較全面,綜合性較強。通過斯諾克臺球的引入,將著重分析兩個等質量的小球間的碰撞情景。首先需要學生能將生活常見過程與碰撞模型相鏈接,然后能根據頻閃照相的簡化圖分析碰前碰后兩小球的運動情況。

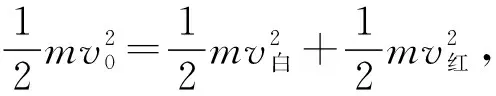
【答案】C

(作者姓名、單位：劉娟 武漢市第十二中學)

4.(多選)2022年2月18日,我國選手谷愛凌在女子U形場地技巧決賽中贏得冠軍。決賽中某時刻,谷愛凌從A點沖出場地,此時速度大小為v=12.5 m/s,與豎直方向夾角為θ=37°。在豎直平面運動后落到B點,同時完成左轉900°動作,如圖6。設C點為最高點,運動員質量為52 kg,重力加速度g=10 m/s2,忽略空氣阻力。下列說法正確的是 ( )

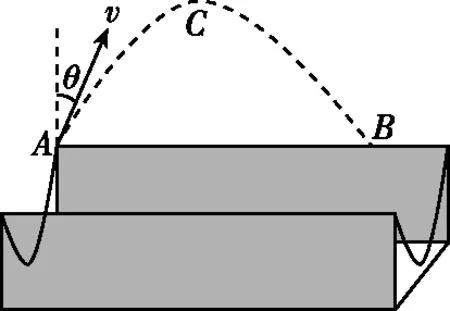
圖6

A.最高點C至A的豎直高度為5 m

B.若運動的同時自身做勻速圓周運動,則空中左轉的角速度為2π rad/s

C.A點至B點的距離為15 m

D.從A點至C點重力勢能增加了2 500 J

【試題分析】根據U形場地技巧決賽實際情境,觀察運動中的物理規律。飛出場地后做斜拋運動,同時左轉900°做勻速圓周運動,類似于地球的自轉。通過計算斜拋運動的豎直高度,讓學生對這種運動的高度有所了解,體會比賽的不易。計算左轉的角速度,讓學生體會是否感到暈眩。計算水平距離,有助于估算U形場地的長度。考查重力勢能的計算,體會到能量的轉化。豎直方向根據自由落體運動規律求得高度及運動總時間,水平方向根據勻速直線運動規律求得水平距離。由角速度的定義式可求得角速度大小。最后根據重力做負功,可求得重力勢能的增加量。

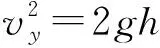
【答案】AC

(作者姓名、單位：劉永陽 陜西省旬邑縣中學)

圖7

圖8

解：流體在與巖石相互作用時,由于其動量發生變化,產生與巖石的相互作用力。

設在一段時間t內,有鉆井液噴射的體積為

V=Qt

噴射鉆井液的質量為m=ρV

鉆井液的動量變化大小Δp=mv1+mv2

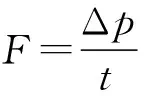
聯立解得F=660 N

(作者姓名、單位：郭明林 大理白族自治州民族中學)

6.2022年2月15日,在第24屆冬奧會男子單板滑雪大跳臺決賽中,中國選手蘇翊鳴獲得金牌,成為我國歷史上最年輕的冬奧冠軍。圖9為示意圖,賽道由出發區(PA段)、助滑區(AB段)、起跳臺(CD段)、著陸坡(EM段)、終點區(MN段)五部分組成。假設出發區PA與平面FE的落差h1=48 m,平面FE與終點區MN的落差為h2=36 m,水平滑道BC長度L=36 m,助滑區與著陸坡均為傾斜的坡面,且坡面傾角均為37°,起跳臺為一圓弧面,其左端C點與助滑區的底端B點在同一水平面上,圓弧所對應的圓的半徑為20 m,圓心角為37°。設在某一次訓練中,運動員由A點靜止出發,經起跳臺起跳后,騰空高度(重心距D點的豎直高度差)為Δh=8 m,最后落在著陸坡上,且落點離坡底M點的距離為30 m,設運動員與滑板的總質量為50 kg,運動員在比賽中可近似地看作質點,且經過賽道的各個連接處時不考慮能量損失,滑板與賽道AB、BC間的動摩擦因數相同,滑板與起跳臺CD間摩擦力不計,不計空氣阻力,取g=10 m/s2。(sin37°=0.6,cos37°=0.8)求：

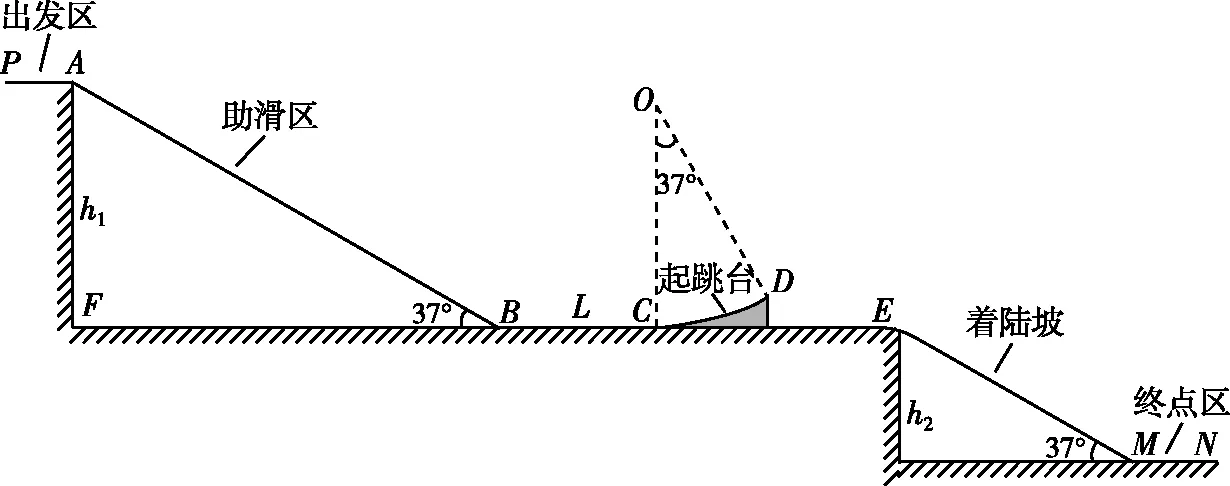
圖9

(1)運動員在離開起跳臺右端D點的速度大小;

(2)運動員在經過起跳臺左端C點時對賽道的壓力大小;

(3)滑板與賽道AB、BC間的動摩擦因數;

(4)運動員在空中能用于完成動作的時間。

解：(1)從D點到最高點,可看作逆向平拋運動,且vD與水平方向夾角為37°,設D點的豎直分速度為vy。

由平拋運動可得

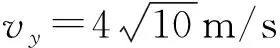
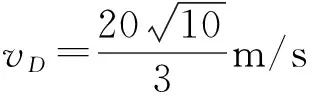
(2)由C到D根據機械能守恒得

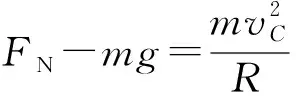
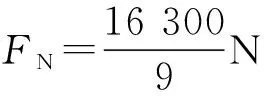
由牛頓第三定律可知,對賽道的壓力

(3)由A到C根據動能定理得

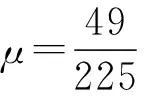
(4)運動員從D點上升至最高點所用的時間

從最高點下落至著落坡時,由圖10可知,總的落差為H=30 m

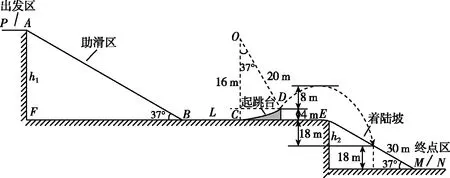
圖10