基于多元線性逐步回歸和BP 神經網絡建立鴨梨盛花期預測模型

王鵬飛，李濤*，于春亮，薛敏，張玉星，張海霞，權暢，許建鋒，馬輝

(1.河北農業大學園藝學院，河北 保定 071000；2.威縣農業農村局，河北 威縣 054700；3.邯鄲市氣象局，河北 邯鄲 056000；4.河北省氣象科學研究所，河北 石家莊 050000)

梨是河北省優質水果之一，截至2021 年底，種植面積達115 466.67 公頃、產量366.6 萬噸、產值140.3 億元，均居全國第1 位。 其中鴨梨作為河北省邯鄲市魏縣主栽品種之一，栽培面積大，歷史悠久，是當地農業的支柱產業之一，近年又通過舉辦“梨花節”等活動進一步助力當地鄉村振興[1]。魏縣鴨梨盛花期集中在早春氣溫變化幅度較大的3 月下旬—4 月上旬，期間若發生“倒春寒”，不僅會造成當年梨果大量減產，也會影響“梨花節”等活動的方案制定和開展。 近20 多年來全球氣候波動明顯，每年觀測到的氣象數據和盛花期時間已明確表明氣候變暖影響到了梨花期[2]，使梨花期提前，導致遭遇“倒春寒”的概率進一步增大[3，4]。 因此，利用多年連續觀測的鴨梨花期資料和氣象數據建立模型對鴨梨盛花期進行預測，是預防“倒春寒”和制定“梨花節”活動預告的重要前提[5]。

目前已有學者開展了花期預測模型相關研究，大多是基于氣象因子與花期的相關關系進行的。 如劉璐等[6]使用偏最小二乘回歸法分析明確平均氣溫和平均地溫是影響中國北方主產地蘋果始花期的最關鍵主導因子，進一步利用逐步回歸法建立預測模型，誤差小于5 天；柏秦鳳等[7]對0、3、5、10℃活動/有效積溫與始花期進行相關性分析，篩選出影響富士系蘋果花期的氣象因子，并建立了5 個主產區富士系蘋果始花期預測模型；譚靜[8]、馮敏玉[9]等也通過分析氣象因子與花期的相關性，選出顯著影響花期的氣象因子，通過建立多元回歸模型，分別對櫻花、油菜花的花期進行預測，取得了一定成效。

近年來，隨著計算機技術的快速發展，機器學習算法的使用越來越廣泛，已成為現代農業氣象科研和業務開展的重要工具[10]。 例如隨機森林[11]、神經網絡[12]、ARMA[13]等已經較好地應用于蘋果[14]、小麥[15]等的花期預測。 本研究以通過相關分析篩選出的氣象因子作為自變量(輸入層)、盛花期日序數作為因變量(輸出層)，分別利用BP 神經網絡算法、多元線性逐步回歸建立魏縣鴨梨盛花期預測模型，經評價篩選出預測精度較高的模型，以期為預防魏縣鴨梨花期“倒春寒”和保障“梨花節”等相關活動順利開展提供技術支持。

1 數據來源與研究方法

1.1 研究區概況

魏縣位于河北省邯鄲市，地處河北、山東、河南三省交界處，北緯36°03′6″～36°26′30″、東經114°43′42″～115°07′24″，衛河、漳河橫貫縣城。 地勢由西南向東北緩緩傾斜，開闊平緩，海拔45.8 ～58.5 m。 日照時數在1 855～2 373 h 之間，年平均氣溫為13.7℃，年降水量為333.8 ～746.2 mm。 鴨梨種植面積10 000 公頃，總產量達35 萬噸。

1.2 數據來源

2002—2020 年鴨梨逐年盛花期觀測資料和氣象數據，分別由河北省邯鄲市魏縣林果開發服務中心、河北省梨氣象服務中心提供。 其中，氣象數據為魏縣1—3 月氣溫、降水量、積溫、日照時數等氣象因子逐年數據，由河北省氣象局在魏縣建立的國家氣象站(東經114.95°，北緯36.33°)收集；盛花期為逐年觀測記錄資料，以梨樹植株50%以上花朵展開的日期作為盛花期標準[16]。本研究所預測的盛花期并不針對某一個梨園，而是根據魏縣林果開發服務中心提供的全縣鴨梨平均盛花期進行預測的。

1.3 數據處理與分析

將逐年盛花期時間轉化為日序數進行統計分析，即1 月1 日為起始日，日序數為1，以此類推，2 月1 日的日序數為32。 魏縣鴨梨盛花期多集中在3 月下旬—4 月上旬，為了展現預測的提前性，將選擇的各類氣象因子指標計算截止時間定為較歷年最早盛花期(3 月23 日)早13 天的3 月10日。 選用1 月1 日—3 月10 日的逐月與逐旬平均氣溫、平均最高氣溫、平均最低氣溫、平均降水量、平均日照時數及≥0℃活動積溫、≥3℃活動積溫、≥5℃活動積溫、≥10℃活動積溫、≥3℃有效積溫、≥5℃有效積溫、≥10℃有效積溫等氣象因子，通過Pearson 相關性分析選出與盛花期相關性較高的氣象因子用于預測模型建立，并用2021、2022 年預測結果與實際盛花期時間進行對比分析，以驗證模型的預測效果。

氣象因子及盛花期日序數采用Microsoft Excel 軟件進行統計，氣象因子與盛花期的相關性用SPSS 25 軟件、Pearson 法進行分析。

1.4 基于多元線性逐步回歸的建模方法

多元線性回歸(MLR)主要是研究一個因變量與多個自變量之間的線性回歸關系，由多個自變量的最佳組合來預測因變量，但由于自變量之間可能存在多重共線性，因此，本研究利用SPSS 25，采用逐步法，考察引入模型的自變量是否仍然具有統計學意義，以檢驗其是否有繼續保留在方程中的價值，并以P值最小且具有統計學意義為依據進行自變量的引入和剔除。 引入自變量的顯著性概率為P＜0.05，剔除自變量的顯著性概率為P＞0.10。 采用方差膨脹系數(VIF)診斷自變量之間是否存在多重共線性，VIF＞10 表示存在嚴重的多重共線性；對回歸方程進行F 檢驗，若F＞F0.01，則表示建立的回歸方程有效。

1.5 基于BP 神經網絡的建模方法

BP 神經網絡由輸入層、隱含層、輸出層及每層之間的結點連接組成，使用梯度搜索技術并利用反向傳播不斷調整網絡的權值和閾值，最終實現網絡實際值與預測值的誤差最小化[17]。 在網絡設計過程中，隱含層神經元個數的確定十分重要，若隱含層節點數過多，會加大計算量并容易產生訓練過度的問題；若節點數過少，則從樣本中獲取的信息較少，達不到較好的效果[18]。 因此，本研究根據經驗公式[18]確定隱含層節點數(式中k 為輸入層節點數，m 為輸出層節點數，α為[1，10]之間的常數)，以通過Pearson 相關系數篩選出的與鴨梨盛花期相關顯著(P＜0.01)的氣象因子作為輸入層節點，以盛花期作為輸出層，利用Matlab 2018a，建立了3 層前饋型單隱含層BP 神經網絡，用于鴨梨盛花期的預測。

1.6 模型精度評價

以實際鴨梨盛花期觀測資料作為最終的預測精度驗證數據，利用決定系數(R2)、均方根誤差(RMSE)、預測準確率/預測誤差率(Rd(1，2))對預測模型進行精度評價和誤差分析。

式中，n 為盛花期年份數量，y 為實際鴨梨盛花期日序數，y＾為預測鴨梨盛花期日序數，為鴨梨盛花期日序數的均值；Rw表示預測盛花期時間與實際盛花期時間誤差在±1 天和±2 天及在±3 天以上的年份數；Rz表示進行預測的總年份數；當誤差在±1 天和±2 天時，計算的Rd1表示預測準確率；當誤差在±3 天時，計算的Rd2表示預測誤差率。

2 結果與分析

2.1 鴨梨盛花期變化特征

2002—2020 年魏縣鴨梨平均盛花期日序數為90，與之對應的盛花期出現在3 月30 日(平年)或3 月31 日(閏年)。 盛花期最早出現在3月23 日(2002 年)，最晚出現在4 月8 日(2005、2012 年)，最早與最遲盛花期日序數相差16。 有12 年出現在3 月下旬，占總樣本的63.15%；有7年出現在4 月上旬，占總樣本的36.85%。 采用線性傾向估計法對鴨梨盛花期總體變化趨勢進行分析，結果(圖1)表明，2002—2020 年間，鴨梨盛花期日序數呈減少趨勢，即盛花期呈提前趨勢，其線性傾向率為-2.4 d/10 a。

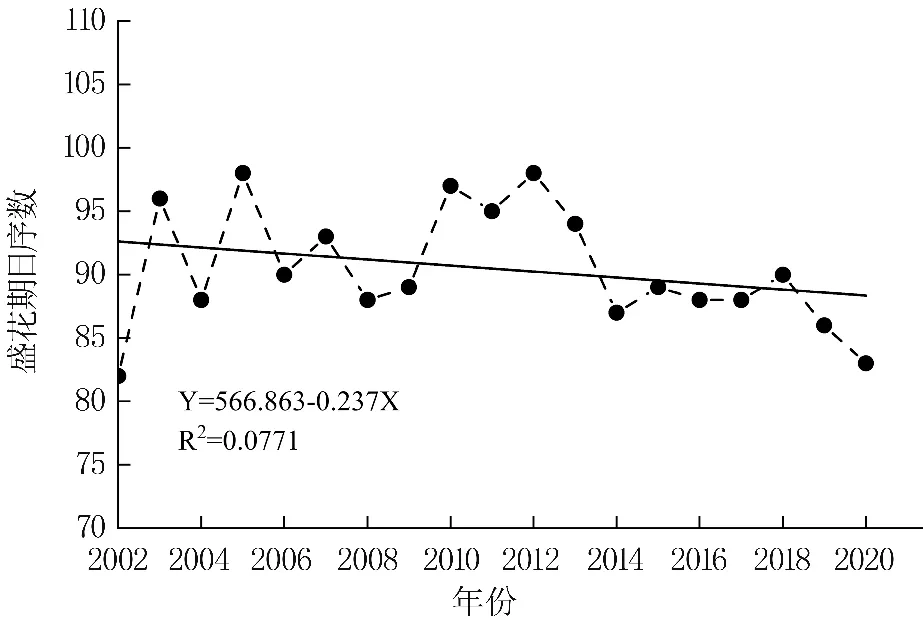
圖1 鴨梨盛花期變化趨勢

2.2 影響鴨梨盛花期的氣象因子篩選

2.2.1 平均氣溫、降水量及日照時數與盛花期的相關性 分別對1—3 月上旬逐月與逐旬的平均氣溫、平均最高氣溫、平均最低氣溫、平均降水量、平均日照時數等共計45 個因子進行分析，結果有16 個氣象因子與盛花期的相關性通過顯著檢驗(P＜0.05)，包括平均氣溫的5 個、最高氣溫的6個、最低氣溫的4 個、降水量的1 個，見表1。 其中，氣溫因子中，鴨梨盛花期與1 月、1 月上旬、3月上旬的平均氣溫和1 月上旬的平均最高氣溫以及1 月、1 月上旬、3 月上旬的平均最低氣溫呈極顯著(P＜0.01)負相關關系，相關系數在-0.626 ～-0.776 之間；1 月平均降水量與盛花期也呈現極顯著相關關系，相關系數為-0.575。 逐月及逐旬日照時數與盛花期未通過顯著性檢驗，1—3 月上旬的日照時數對魏縣鴨梨開花早晚無顯著影響。選擇通過極顯著(P＜0.01)水平的氣象因子作為后續建立預測模型的自變量，共8 個，分別為T1、T2、T5、T7、T12、T13、T15、T16。

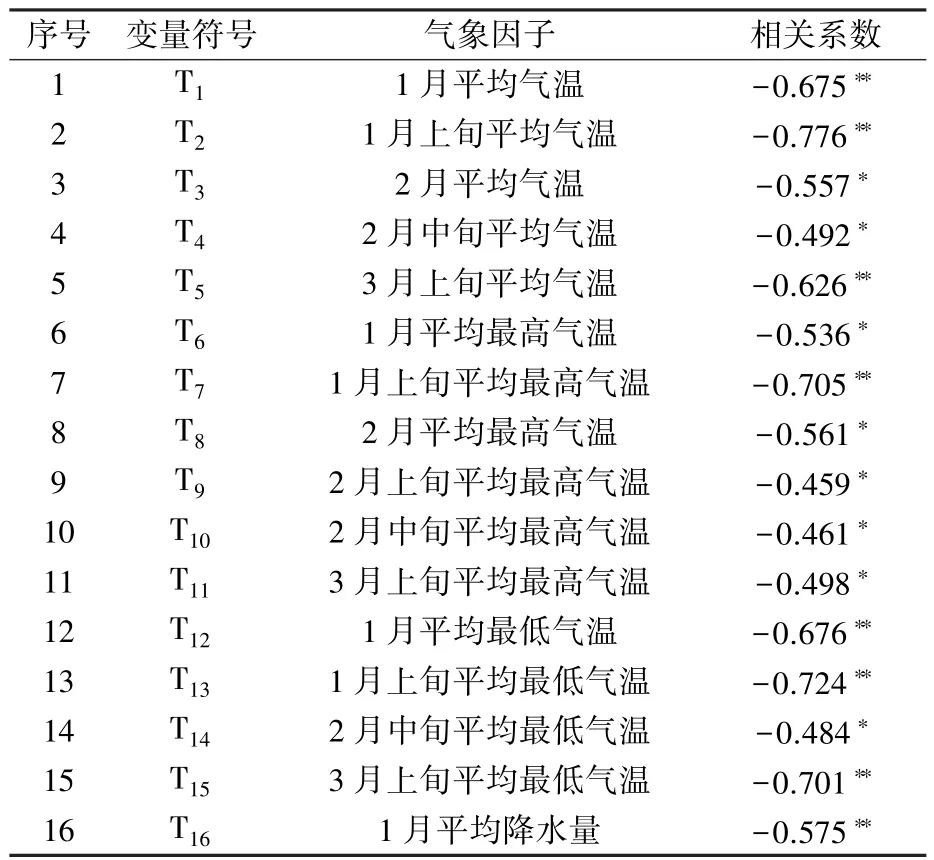
表1 2002—2020 年1—3 月逐月和逐旬氣象因子與盛花期的相關系數

2.2.2 積溫與盛花期的相關性 對1—3 月上旬7 個活動/有效積溫因子與盛花期的相關性進行Pearson 相關分析，結果(表2)表明，僅有5 個積溫因子與盛花期的相關性通過0.01 水平顯著檢驗，分別為≥0℃活動積溫、≥3℃活動積溫、≥5℃活動積溫、≥3℃有效積溫、≥5℃有效積溫，用于后續建立預測模型。 其中，活動積溫與盛花期之間呈現較強的負相關關系，相關系數為-0.820 ～-0.852，即≥0℃、≥3℃、≥5℃活動積溫值越大，盛花期越早，反之越遲。

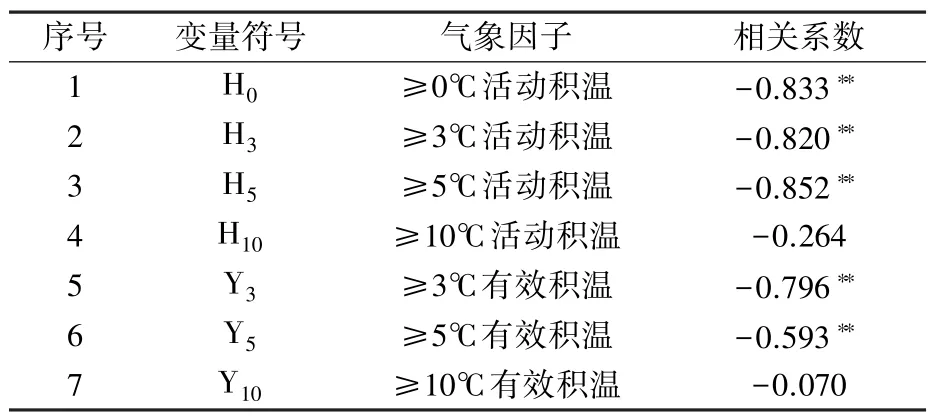
表2 積溫因子與盛花期相關系數

2.3 基于多元線性逐步回歸建立鴨梨盛花期預測模型

2.3.1 多元線性回歸模型的建立 選擇2002—2020 年鴨梨盛花期日序數作為因變量，以上文篩選出的13 個與盛花期極顯著相關的氣象因子作為自變量，利用逐步回歸法進行建模。 經過“逐步法”篩選出≥5℃活動積溫、≥5℃有效積溫、1月平均降水量、1 月上旬平均氣溫仍然存在嚴重的共線性，由于≥5℃活動積溫與盛花期的相關性極強，所以剔除掉≥5℃有效積溫，然后再進行逐步回歸，建立了多元線性逐步回歸(MLSR)模型，見式(4)。 表3、表4、表5 分別是對模型中各個系數檢驗和自變量多重共線性診斷結果。 結果表明，自變量VIF 小于10，條件指數在0 ～10 之間，R2＝0.905；模型通過了F 檢驗，F ＝47.631 ＞F0.010(3，15)＝5.42，P＜0.01，自變量通過了t檢驗，即模型回歸顯著，不存在多重共線性。

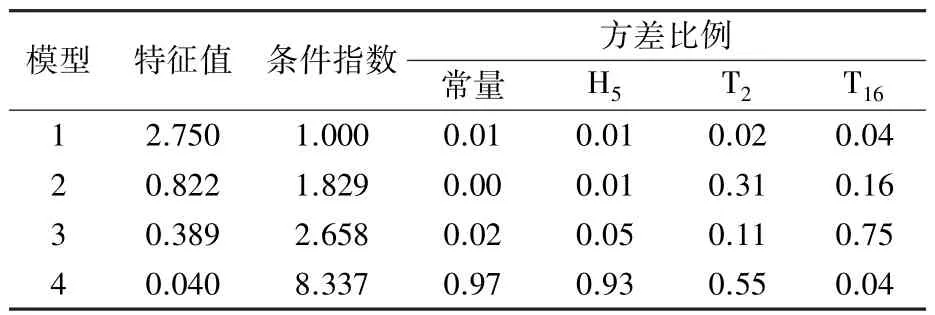
表3 自變量之間多重共線性診斷結果

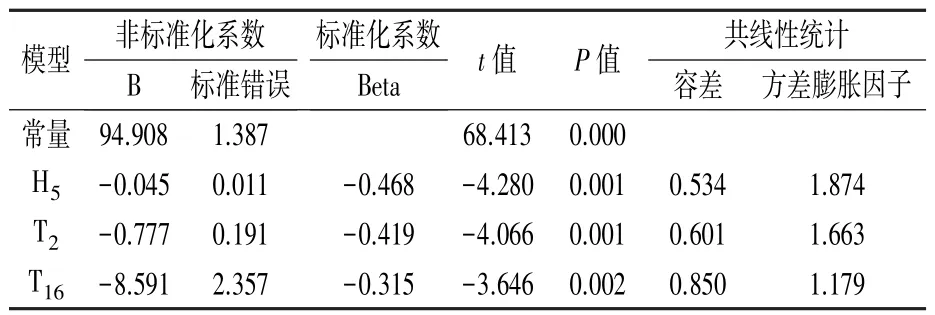
表4 模型系數檢驗結果

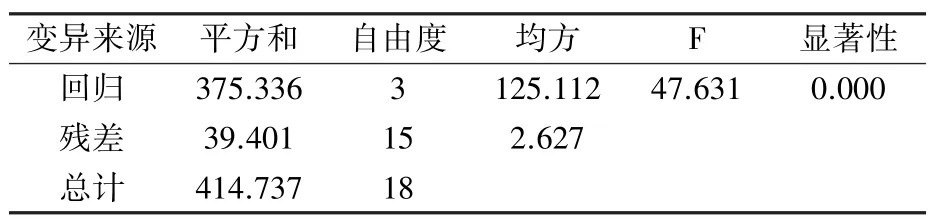
表5 模型方差分析檢驗結果

式中，Y 是盛花期日序數，H5是1—3 月上旬≥5℃活動積溫，T2是1 月上旬平均氣溫，T16是1 月平均降水量。

2.3.2 模型回代檢驗 利用建立的多元線性逐步回歸模型對2002—2020 年盛花期數據進行擬合，結果(表6)顯示，實際盛花期與預測盛花期完全一致年份為2003、2015、2020 年，占15.8%；擬合誤差在±1、±2 天的有15 年，占78.9%；擬合誤差為±3 的僅有2009 年，占5.3%。

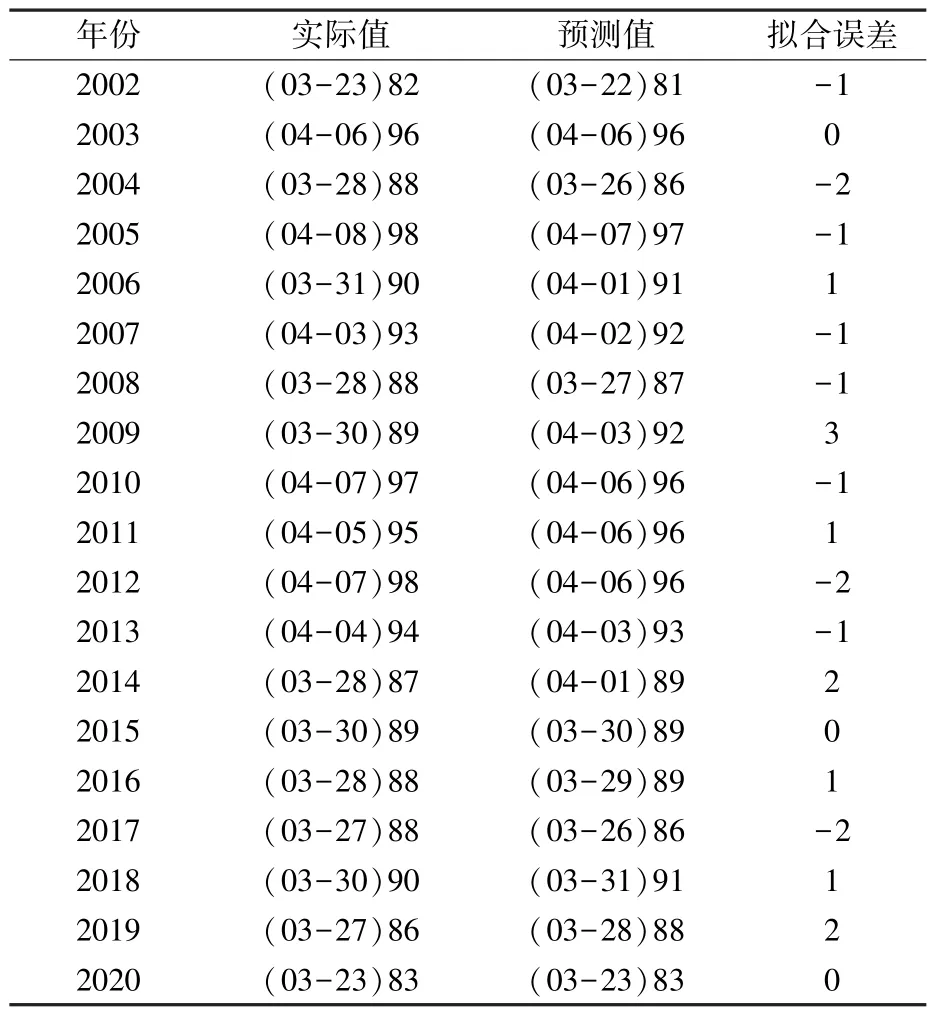
表6 鴨梨盛花期與氣象因子模型回代檢驗

2.4 基于BP 神經網絡建立鴨梨盛花期預測模型

首先將篩選出的極顯著影響盛花期的13 個氣象因子進行歸一化處理，作為輸入層，輸出層為盛花期日序數，然后對氣象因子數據集進行網絡訓練。 采用公式確定隱含層節點數，此處k ＝13，m ＝1，α為[1，10]之間的常數，確定隱含層節點數選取區間為[4，13]。 通過10 次試驗結果(表7)可見，當隱含層個數為10 時，訓練誤差最小，為0.0084，訓練結果最佳。

表7 不同隱含層節點數的訓練誤差

神經元傳遞函數采用非線性的激活函數tansig，其收斂速度快，可以有效減少迭代次數。 訓練算法采用Trainlm 函數，訓練次數1 000 次，學習速率設為0.01，訓練目標最小誤差設為0.001，輸出層神經元傳遞函數采用Purelin 函數。

選擇2002—2016 年數據為訓練集進行訓練，2017—2020 年數據進行測試。 通過計算盛花期預測值與實測值的相關系數，訓練集樣本兩者間的相關系數都在0.860 ～0.972 之間，因此，根據測試集相關系數高低來選擇模型，最終選出訓練集R2＝0.970、測試集R2＝0.700 的模型為最佳模型，訓練集、測試集預測誤差均在±2 天以內(圖2—5)，未出現誤差為±3 天的年份，預測精度較高，較好地模擬出2002—2020 年實際盛花期與預測盛花期的波動變化。

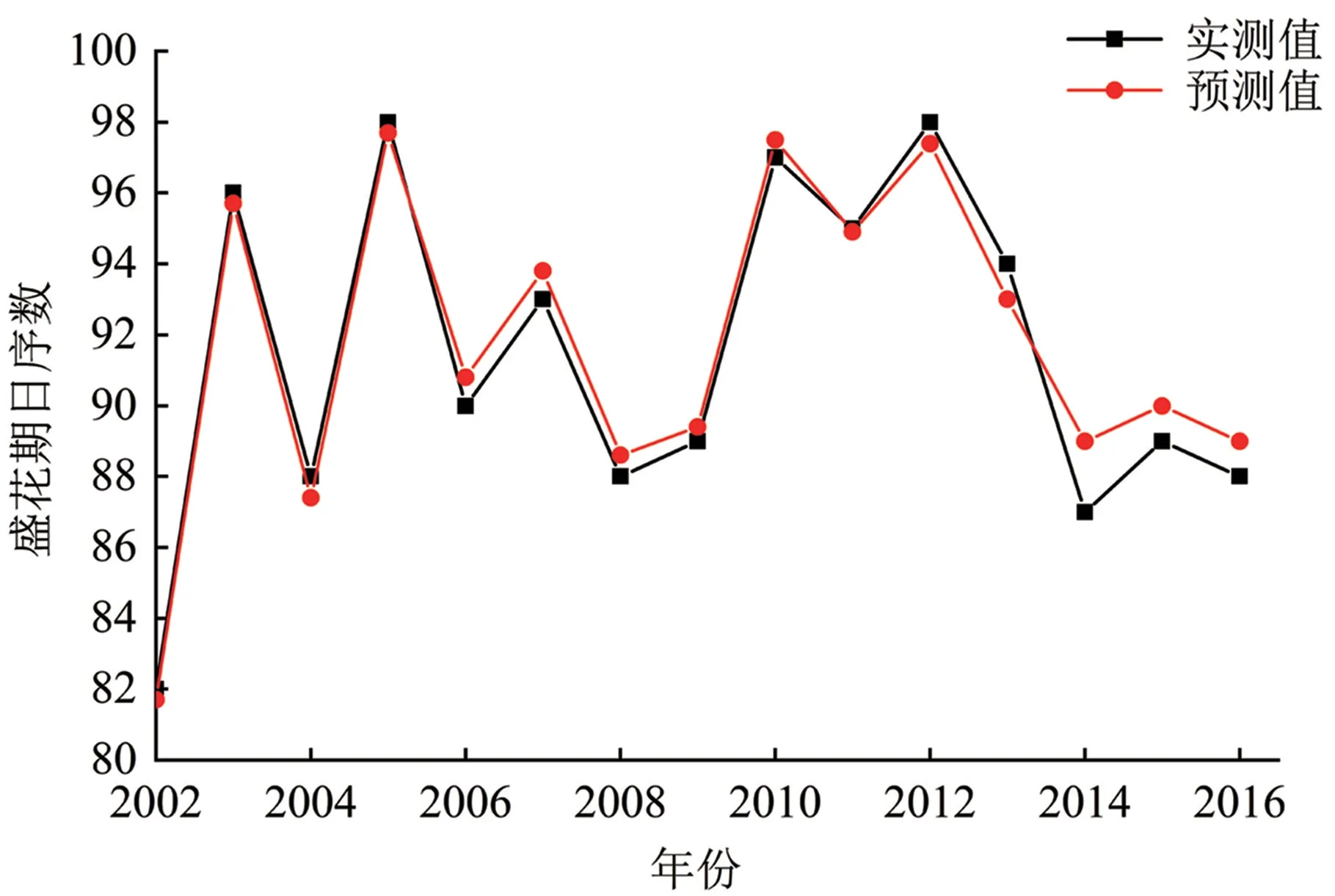
圖2 訓練樣本實測值與預測值

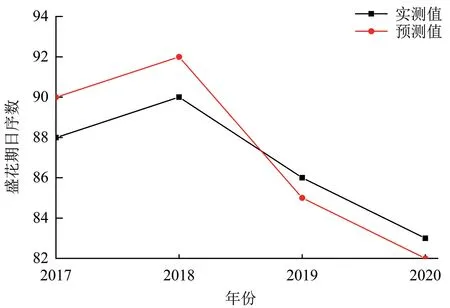
圖3 測試樣本實測值與預測值

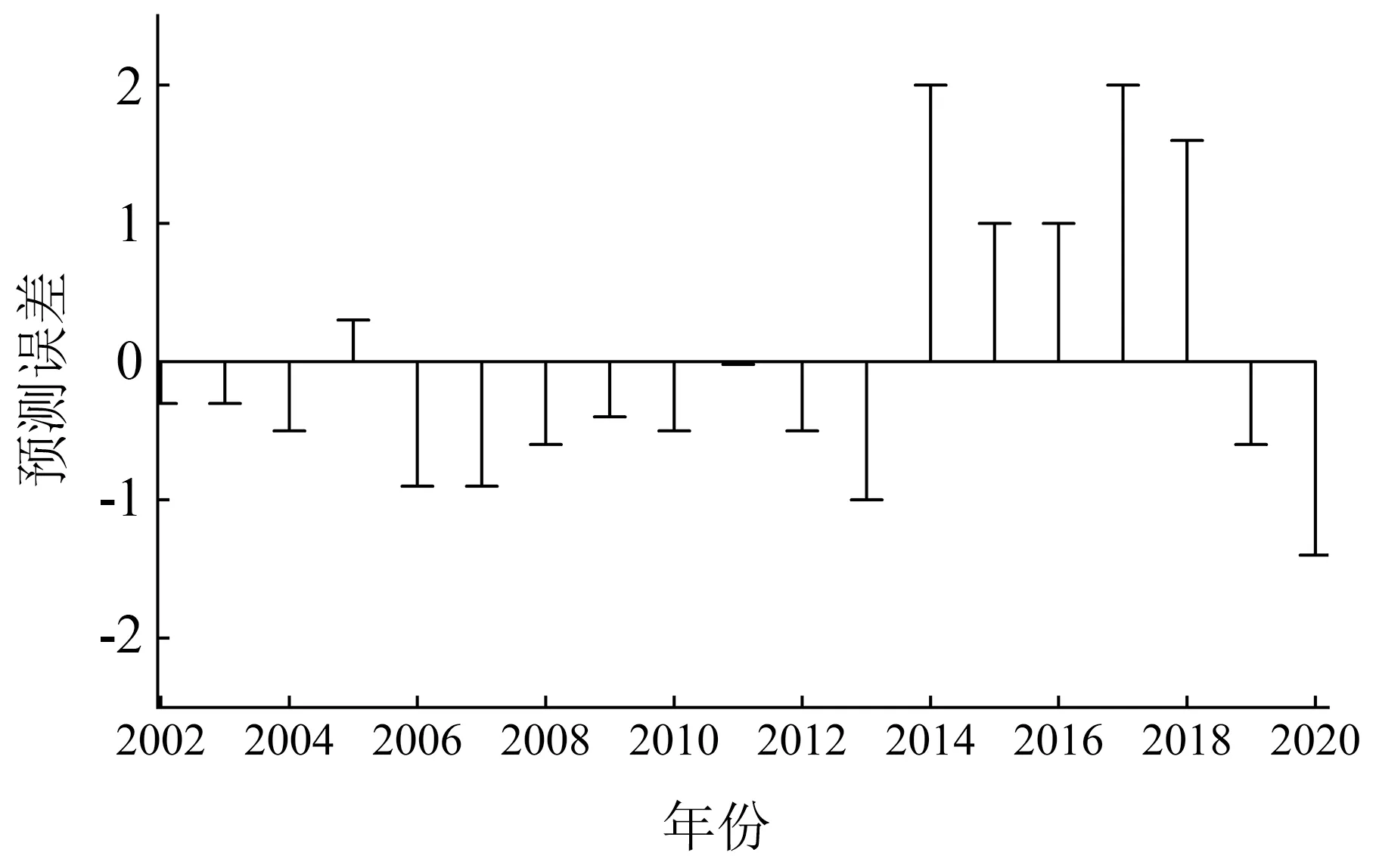
圖4 訓練集樣本誤差

2.5 兩種模型預測精度的比較評價

通過計算決定系數(R2)、 均方根誤差(RMSE)、預測準確率(Rd1)、預測誤差率(Rd2)，比較兩種鴨梨盛花期預測模型精度，R2越高，RMSE 越小，Rd1越高，預測效果越好。 由表8 可知，BP 神經網絡模型的R2為0.950，明顯高于多元線性逐步回歸模型的R2值(0.905)，說明BP 神經網絡模型對盛花期波動趨勢擬合度更高；進一步分析兩種模型的RMSE、Rd1、Rd2表明，基于多元線性逐步回歸的RMSE 為1.45，Rd1為94.7%，Rd2為5.3%。 BP 神經網絡RMSE 為1.05，Rd1為100%，Nd2為0。 對比發現，基于BP 神經網絡建立的預測模型對鴨梨盛花期的預測精度較高。

表8 兩種建立模型預測精度檢驗

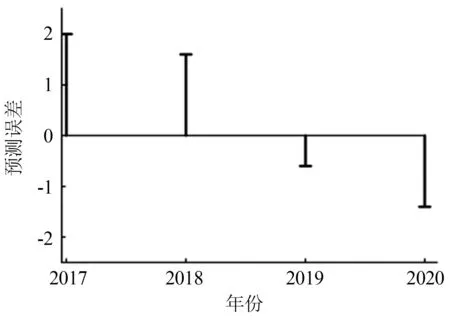
圖5 測試集樣本誤差

2.6 兩種建立模型對2021、2022 盛花期的預測效果

利用2021、2022 年的數據對建立的多元線性逐步回歸、BP 神經網絡模型的預測效果進行驗證，結果(表9)顯示，多元線性逐步回歸模型預測的2021 年盛花期在第84 天，與實際盛花期(2021年3 月23 日)日序數誤差為2 天；2022 年盛花期在第86 天，與實際盛花期(2022 年3 月27 日)相符。 BP 神經網絡模型預測的2021 年盛花期在第82 天，2022 年盛花期在第86 天，均與實際盛花期觀測值相符。 總體來看，兩種模型都能很好地預測出2021、2022 年的盛花期時間，且誤差較小，尤以BP 神經網絡模型的預測準確度更高。

表9 兩種建立模型預測效果的驗證結果

3 討論

篩選顯著影響花期的氣象因子是建立預測模型的基礎及提升預測精度的有效方法。 前人研究認為植物花期與其前期氣象因素顯著相關[19-25]，其中溫度是影響花期的重要因素。 因此，本研究通過分析鴨梨盛花期與前期的平均氣溫、平均最高氣溫、平均最低氣溫、活動/有效積溫、平均降水量、平均日照時數等氣象因子的相關性，篩選出13 個與鴨梨盛花期極顯著相關的氣象因子作為預報因子，用于預測模型構建。 這13 個因子中，1 月上旬的平均氣溫、平均最高氣溫、平均最低氣溫、1 月平均降水量與鴨梨盛花期負相關的程度最高，可能與當地的氣候條件及地理位置有關；1—3 月上旬的≥5℃活動積溫與盛花期相關關系最為緊密，這與郭連云[26]、郭睿[23]等的結論相符，即完成某一發育期需要一定數量的積溫。

建模方法是影響鴨梨盛花期預測精度的一個重要因素。 在多元線性回歸分析中，由于入選的自變量之間容易存在共線性，需要采用“逐步法”剔除冗余信息，以確保自變量之間不存在高度相關性，該算法不僅可以簡化計算過程，更能顯著提升花期預測模型精度和可靠性[27]；但隨著樣本數量和自變量的增多，入選的影響花期早晚的因素可能較少，從而導致預測精度不高。 BP 神經網絡作為一種按照誤差逆向傳播算法訓練的多次前饋網絡，不僅可以儲存和學習大量的數據輸入和輸出，而且不需對變量的映射關系進行表述，具有處理非線性能力；應用反向傳播途徑不斷調整網絡的閾值與權值，直到滿足誤差最小精度條件，輸出最優結果[18，28]。 傳統的回歸模型需要人為選擇被預測變量與預測變量之間的模型形式，尤其在數據量較大的情況下，更難選擇一個合適且具有代表性的預測模型，所以，在實際應用過程中往往選擇簡單的多元線性回歸模型，但預測精度降低；而BP 神經網絡只要建模數據有足夠的代表性，利用網絡自身的學習能力和速算能力，可以得到一個預測效果比較好的模型。 本試驗對魏縣鴨梨盛花期的預測結果表明，BP 神經網絡預測模型要優于多元線性逐步回歸模型。

本研究所建立的模型僅適用于魏縣整個區域的鴨梨盛花期預測，而每個梨園的管理水平、地勢、地溫、樹勢等條件存在差異，也會影響盛花期，后期有必要針對單個梨園開展更精準的花期預測。

4 結論

魏縣地區2002—2020 年的19 年間鴨梨盛花期總體呈現提前趨勢，每10 年平均提前2.4 天。1 月平均氣溫、1 月上旬平均氣溫、3 月上旬平均氣溫、1 月上旬平均最高氣溫、1 月平均最低氣溫、1 月上旬平均最低氣溫、3 月上旬平均最低氣溫、1 月平均降水量及1—3 月上旬的≥0℃、≥3℃、≥5℃活動積溫和≥3℃、≥5℃有效積溫與鴨梨盛花期極顯著負相關，相關系數在-0.575 ～-0.852。逐步多元線性回歸、BP 神經網絡兩種預測模型均可在3 月上旬提前預測盛花期，基于最早盛花期可以提前13 天預報，基于最晚盛花期可以提前29 天預報。 其中，BP 神經網絡模型的預測精度更高。