基于APOS理論的零點存在性定理教學要點

魏素云　易桂生

一、APOS理論要義

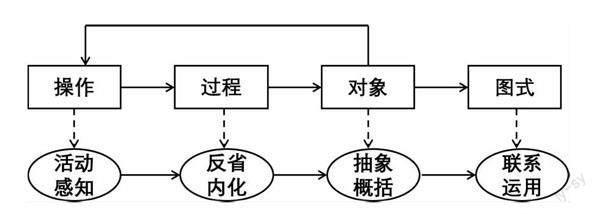
APOS理論是由美國的杜賓斯基等人在數學教育與研究實踐中發展形成的.該理論依據學生學習的心理建構過程，提倡教師在教學中，應以學生為主體，讓學生主動探究、理解和掌握知識.其教學流程如圖所示：

“操作”階段（Action），學生需要通過操作來感知事物，理解所學內容的意義.通過操作，學生對何為函數零點和零點存在的條件會有一定的感性認識，同時，教師應向學生提供符合函數零點存在性定理學習的材料或者情景動畫，并相應地設計出適合學生探究的學習活動，由此為歸納概括所學概念提供建構的固著點.

“過程”階段（Process），強調學習者應把“操作”階段中的感受進行反省內化.老師教學中，可以用問題串的形式，幫助學生從操作對象中跳出來，引發學生的思維逐步深入.

“對象”階段（Object），學生通過對數學活動的思考、分析、比較及抽象之后得到函數零點的概念和零點存在性定理的條件，并在教師的引導下能用較嚴謹的數學語言準確地表述出其定義及存在性定理.

“圖式”階段（Scheme），學習者頭腦中函數零點相關內容將以一種綜合的圖式呈現，并在其知識體系中占據獨特的位置.這一階段，學生對函數零點的概念有較為完整的認知結構或認知框架，教師在教學中相應地應可通過練習讓學生達到對函數零點存在性定理的理解，由此幫助學生形成零點概念的整體圖式.

二、教學目標及重、難點

1.教學目標

（1）能在結合具體的實例中，掌握函數零點的定義.

（2）能借助操作活動，歸納總結出“函數零點存在性定理”，并能理解該定理的條件.

（3）在辨析和操作的過程中感悟其數學思想方法，并養成嚴謹性的學習習慣、提高數學抽象和直觀想象素養.

2.重點：函數零點存在性定理.

3.難點：函數零點存在條件的探究.

三、定理的教學過程

1.新課引入

問題1 2x－y－6=0表示什么？x=3表示什么？

預設：2x－y－6=0表面上看是方程.同時x=3也是二元一次函數與x軸交點的橫坐標.

問題2 方程2x+2x－6=0是否有實根？

預設：部分學生會把該方程轉化為兩個函數y=2x與y=－2x+6，再數形結合判定出方程根所在的區間范圍，也有學生想通過作出y=2x+2x－6的圖像，但發現很困難.

設計意圖：問題1主要是為函數零點概念做鋪墊，更重要的是引導學生認識到方程與函數之間的特殊關系.問題2則是引發學生的認知沖突.

2.感知定理

方程和函數可以互相轉化，求方程的根就是求函數與x軸的交點的橫坐標.

讓我們在直角坐標系中畫一畫，以線條來代替函數曲線，怎樣畫曲線才能與x軸有交點？

預設：師生根據圖像，選擇有交點的情況，并引導學生進行分類討論.

問題3 什么條件下與x軸一定有交點呢？

預設：端點一上一下的時候.

問題4 在直角坐標系中怎樣判斷端點是在x軸一側呢？

預設：根據函數值的符號來判斷.

問題5 我們如何用一個統一的式子來表達A、B兩點函數值是異號呢？

問題6 具備上述特征的函數y=fx的圖像與x軸在區間a，b上一定有交點嗎？

設計意圖：將函數零點存在性定理作為解決課堂探究問題的過程性知識，讓學生在動態操作中觀察，探索和發現函數端點處的函數值，函數連續性對定理的影響.

3.定理形成

總結：對于函數y=f（x），把使f（x）=0的實數x叫做函數的零點.若函數y=fx在閉區間a，b上的圖像是連續曲線，并且在區間端點的函數值符號相反，即f（a）·f（b）<0，則f（x）在區間a，b內至少有一個零點.

設計意圖：關注學生判定定理的形成過程，通過問題串，引導學生的思維逐漸深入，經歷從具體到抽象并歸納總結出零點的判定定理.

4.定理辨析

結合函數圖象，判斷以下命題的正誤性，若不正確，請通過函數圖像舉出反例.

（1）若函數y=fx 在a，b上滿足f（a）·f（b）<0，則它在區間a，b內一定有零點.

（2）若函數y=f（x）在a，b上的圖象連續，且它在區間a，b內有零點，則f（a）·f（b）<0.

（3）若函數y=f（x）在a，b上的圖象連續，且f（a）·f（b）<0，函數y=f（x）在區間a，b內存在唯一零點.

設計意圖：通過以上判斷既是對學習活動情況的總結，又是對函數零點存在性定理作進一步的認識，（1）函數圖象連續；（2）結論不可逆；（3）零點個數不確定.由此讓學生的學習能達到概念的精致化目的.

5.定理運用

另一方面，由于2x單調遞增而2x－6也單調遞增，因此fx=2x+2x－6單調遞增，所以該函數在1，2內恰有一個零點.

預設：本變式可通過學生練習并板書講解完成.

設計意圖：本例題及變式目的是強化通過兩個函數圖象的交點問題，解決根的存在及個數問題，并將函數的單調性與函數零點融入其中形成知識組塊.

四、結語

APOS理論強調在數學教學中應該關注過程，教師要給學生抽象概括的機會，讓學生從大量的事例中觀察、分析、抽象概括出它們的本質屬性.教學中應突出強調學生應經歷一個從“形”到“數”的認識過程.由此達到深入把握數學內容的本質.在教學中教師重點在于促進學生的思考，設計出以知識的產生和發現的主線、并以知識產生的必要性與合理性為著力點，努力用問題引導實施教學.