一道八省聯(lián)考解析幾何題的解法探秘

魯和平

(浙江省嘉善第二高級中學,浙江 嘉興 314100)

題目(2021年八省聯(lián)考數(shù)學試題第7題)如圖1,已知拋物線y2=2px上三點A(2,2),B,C.直線AB,直線AC是圓N:(x-2)2+y2=1的兩條切線,則直線BC的方程為( ).

圖1 2021年八省聯(lián)考第7題圖

A.x+2y+1=0 B.3x+6y+4=0

C.2x+6y+3=0 D.x+3y+2=0

1 題目解析

解法1(直譯法) 將A(2,2)代入y2=2px,得p=1.

故拋物線方程為y2=2x.

設過A(2,2)的切線方程為

y-2=k(x-2).

即kx-y+2-2k=0.

代入y2=2x,整理,得

故yB+yC=-4.

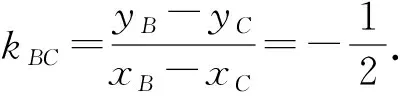
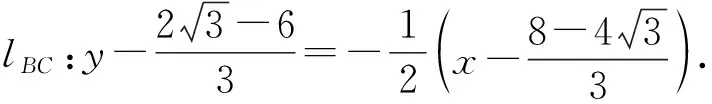
即3x+6y+4=0.

故選B.

解法2(韋達定理法)

即2px-(yA+yB)y+yAyB=0.

這里p=1,xA=2,yA=2,

故lAB:2x-(2+yB)y+2yB=0.

因為直線AB與圓N:(x-2)2+y2=1相切,

①

②

由①②可知:yB,yC是方程3y2+12y+8=0的兩個不等的實根,

代入2x-(yB+yC)y+yByC=0,得

直線BC的方程為3x+6y+4=0.

解法3(軌跡法) 由解法2知

3·(2xB)+12yB+8=0.

即3xB+6yB+4=0.

③

同理可得3xC+6yC+4=0.

④

由③④可知

點B與點C均在直線3x+6y+4=0上.

故直線BC的方程為3x+6y+4=0.

代入y2=2x整理,得

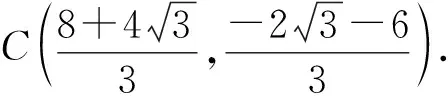
由兩點式得直線BC的方程為3x+6y+4=0.

解法5(拋物線參數(shù)方程法)因為拋物線方程為y2=2x,設B(2t2,2t),

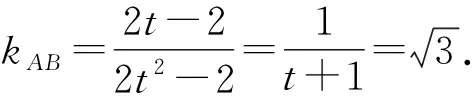
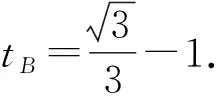
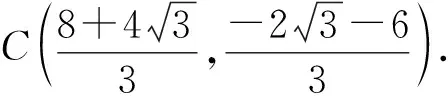
由兩點式得直線BC的方程為3x+6y+4=0.

圖2 張角定理圖 圖3 解法6圖

代入y2=2x整理,得

如圖3,由張角定理,得

將點E坐標代入四個選項,檢驗知B正確.

解法7(導數(shù)法) (1)首先證明以下命題:

已知拋物線C:y2=2px,定點A(x0,y0)∈C,動點P(x1,y1)∈C,Q(x2,y2)∈C,kAP+kAQ=0,則kPQ為定值,且等于拋物線在點A處切線斜率的相反數(shù).

代入kAP+kAQ=0整理,得2p(y1+y2+2y0)=0.

故y1+y2=-2y0.

又因為y2=2px,所以2yy′=2px.

所以kPQ=-kA.故命題得證.

由直線的點斜式方程,得

BC的方程為3x+6y+4=0.

(2)如圖4,作出點A關于x軸的對稱點A1(2,-2).

圖4 解法7(2)示意圖

由y2=2x得拋物線的下半支的方程為

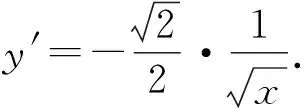
所以過點A1(2,-2)的切線的斜率為

由拉格朗日中值定理,知

由點斜式得直線BC的方程為

3x+6y+4=0.

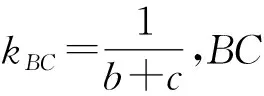
故直線BC的方程為

整理,得x-(b+c)y+2bc=0.

所以b,c是方程3x2+6x+2=0的兩根.

即3x+6y+4=0.

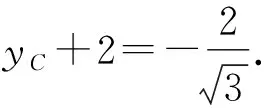
由點斜式得直線BC的方程為3x+6y+4=0

則由AB,AC構成的二次曲線方程為

化簡,得3(x-2)2-(y-2)2=0.

代入上式,得(y-2)2(3y2+12y+8)=0.

將y2=2x代入,得

(2x-4y+4)·(6x+12y+8)=0.

又因為過點A的切線方程為x-2y+2=0,

且直線AB,AC構成的曲線與拋物線的交點是A,B,C三點,

所以直線BC的方程為3x+6y+4=0.

解法10(待定系數(shù)法)由拋物線,直線AB,AC構成的二次曲線方程為

①

化簡整理,得

-3λx2+(λ+μ)y2+(12λ-2μ)x-4λy-8λ

=0.

因為過點A的切線方程為x-2y+2=0,

設直線BC:ax+by+c=0,

則由過點A的切線、直線BC構成的二次曲線方程可設為

(x-2y+2)(ax+by+c)=0.

化簡整理,得

ax2-2by2+(b-2a)xy+(c+2a)x+(2b-2c)y+2c=0.

②

即3x+6y+4=0.

數(shù)學學習離不開解題的研究,而對于數(shù)學問題的解決不能僅停留于得出答案層面,更重要的是引導學生進行多向思維[1].同一題目從不同角度進行研究往往會有不同的發(fā)現(xiàn),進而會有不同的解題方法,所以應在拓展思路的過程中培養(yǎng)學生的發(fā)散思維,結合題目中的已知條件發(fā)現(xiàn)解決問題的關鍵,并有效地鞏固基礎知識,掌握解題技巧,提高學生分析問題、解決問題的能力.