非線性模型的抗差最小二乘法及其在圓心擬合中的應用

李春雷,王亞男,葛仁磊,陳珣

(海洋石油工程股份有限公司,山東 青島 266555)

圓形及圓柱是最常見的自然曲面之一,在各類工程中得到了非常廣泛的應用,使用測量數據計算結構物的圓心坐標也是工程及工業(yè)測量中最基本的任務之一。在實際測量工作中,粗差往往不可避免,但在圓心計算中,即使錯誤數據只占所有測量數據很小的一部分,也會導致計算結果產生較大的偏離。

解決此問題最常用的方法是對測量數據進行人工檢查,剔除其中的粗差點,然后再進行后續(xù)計算。但此過程由于需要人為干預,導致效率較低,而且由于不同的數據處理人員的主觀意識影響,也會使不同的數據處理人員得到的數據處理結果各不相同,難以統(tǒng)一。

抗差最小二乘法就是為了解決粗差數據對處理結果影響過大的問題而提出的。抗差最小二乘法最基本的原理是在最小二乘法的基礎上,使用測量數據自動產生等價權,并根據不同的原則調整后驗權,使粗差點對結果的影響減弱甚至消除精差點的影響。

1 選權迭代法

最小二乘原則在測量平差中得到了非常廣泛的應用。但是,當觀測值存在粗差時,最小二乘原則就會出現明顯的不適應性,即單個測值的偏差即可能導致結果面目全非[1]。基于此,抗差最小二乘法應運而生。抗差最小二乘法是在最小二乘法的基礎上,通過改變觀測值的權重,以減少甚至消除觀測值中粗差的影響。

進行測量數據平差時最常用的方法是間接平差法,間接平差的誤差方程為[2]:

V=AX-L

根據條件平差理論,不僅可以對未知參數X進行估計,還可以對未知參數X的后驗權進行估計,X及其后驗權陣為PXX的估計值為[2]:

X=(ATPA)-1ATPL

PXX=ATPA

假設觀測值中有一個粗差i,根據中誤差σi與權pi的關系[2]:

在一次計算中,單位權中誤差σ0固定,也就是說觀測值的方差越大,則其權就越小。也就是說使用后驗權陣PXX當作權陣再進行一次平差,粗差i對結果的影響就會變小,未知參數X的估計就會更接近真值。如果我們反復迭代,那么粗差的影響會越來越小,未知參數X的估計也會越來越接近真值。

上述做法就叫做選權迭代法[3-4],其選權原則為最小二乘法原則,即:

上式中:pi為PXX的第i個對角素;νi為向量V中第i個元素。

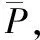
顯然,對于最小二乘原則:

wi=1

2 常用選權原則

最小二乘原則是抗差最小二乘法中最常用的一種原則,第1節(jié)中已經作了詳細介紹,這里就不作贅述。下面就繼續(xù)為大家介紹兩種常用原則。

2.1 殘差絕對和最小原則

殘差絕對和最小原則的估計準則為:

相應的權因子為[3]:

在實際計算中,為了避免由于νi≈0時造成計算錯誤,一般使用下式來計算:

c一般取比較小的值,在實際使用中常取c=0.001。

殘差絕對和最小原則的抗差性非常好,其崩潰污染率高達50%,是所有抗差估計類中,是崩潰污染率最大的一種。但其精度并不高,所以常用于初始值的估計[3]。

2.2 IGG Ⅲ選權原則[4]

IGG為中國科學院測量與地理研究所的英文縮寫,IGG Ⅲ方案是基于測量誤差的有界性提出來的,它對測量抗差估計比較有效。其等價權因子取為[4]:

式中,σ0為單位權中誤差。由圖1wi與νi/σ0的關系可以很明確地看出k0和k1的幾何意義。

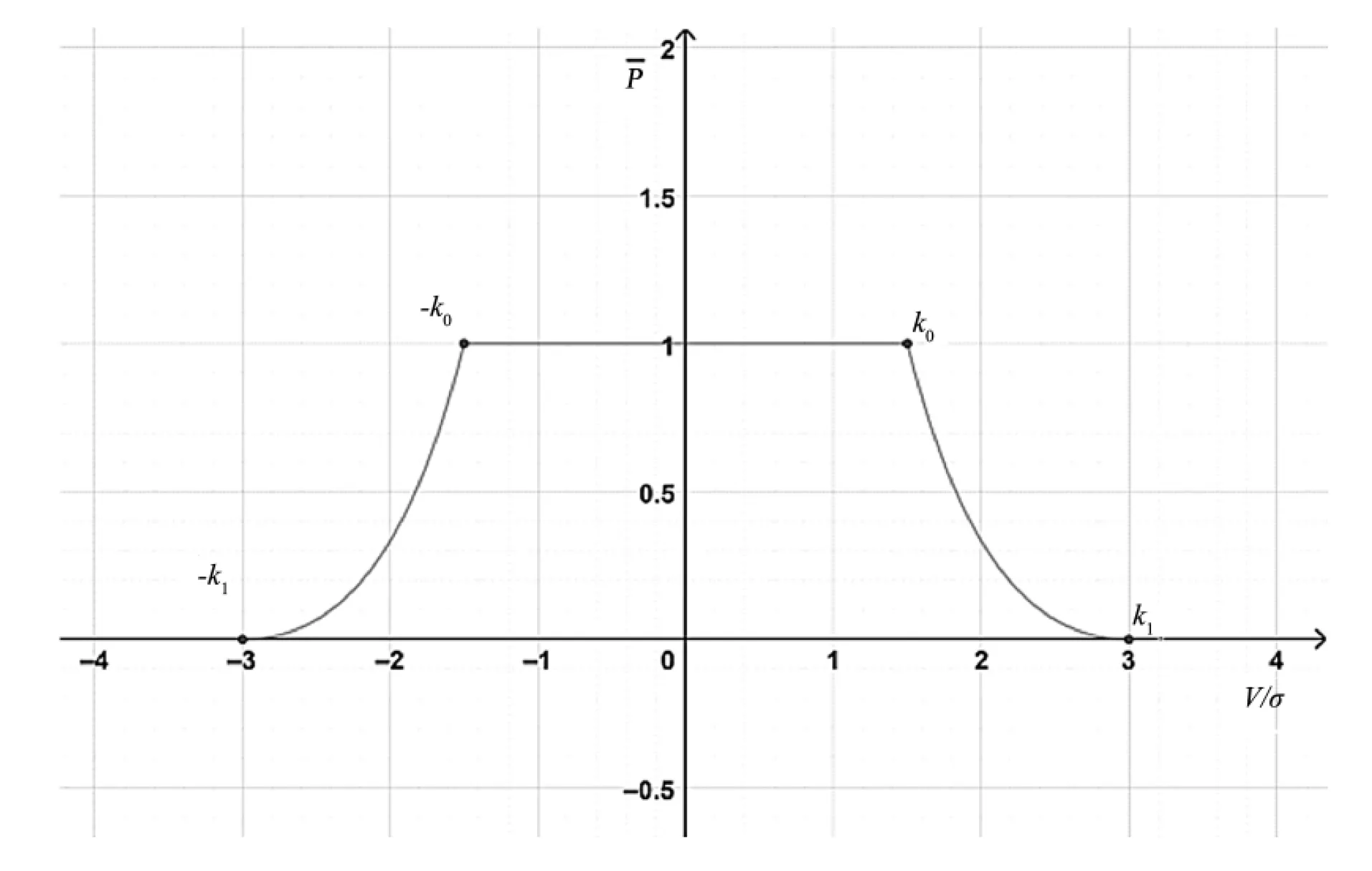
圖1 wi與νi/σ0的關系圖

在抗差最小二乘法中最常用的取值為k0=1.5,k1=2.5。但其取值并不是固定不變的,在精密工程測量與工業(yè)測量中,可以根據實際工程需要對k0和k1進行設置。而且當k0=k1=3時,此等價權設計方案就變成常用的萊因達準則。

3 三步抗差方案[5]

學者利用上述幾種選權方案的優(yōu)點,提出了“三步抗差方案”,之前的討論多在線性模型的基礎上進行的[1,5]。但在實際數據處理工作中,非線性模型則更為常見。非線性模型的引入,會加大大增加三步抗差的復雜度。在本文根據工程測量實際,對三步抗差方案進行適當的簡化,并介紹非線性模型的三步抗差方案。

同線性模型一樣,三步抗差方案分為初值選取階段、粗差剔除階段及結果優(yōu)化階段。

3.1 初值選取階段

此階段的目標是選擇抗差性能優(yōu)良的初始值。根據前文的探討,此階段使用殘差絕對和最小原則進行初值的選取。選擇過程如圖2所示。

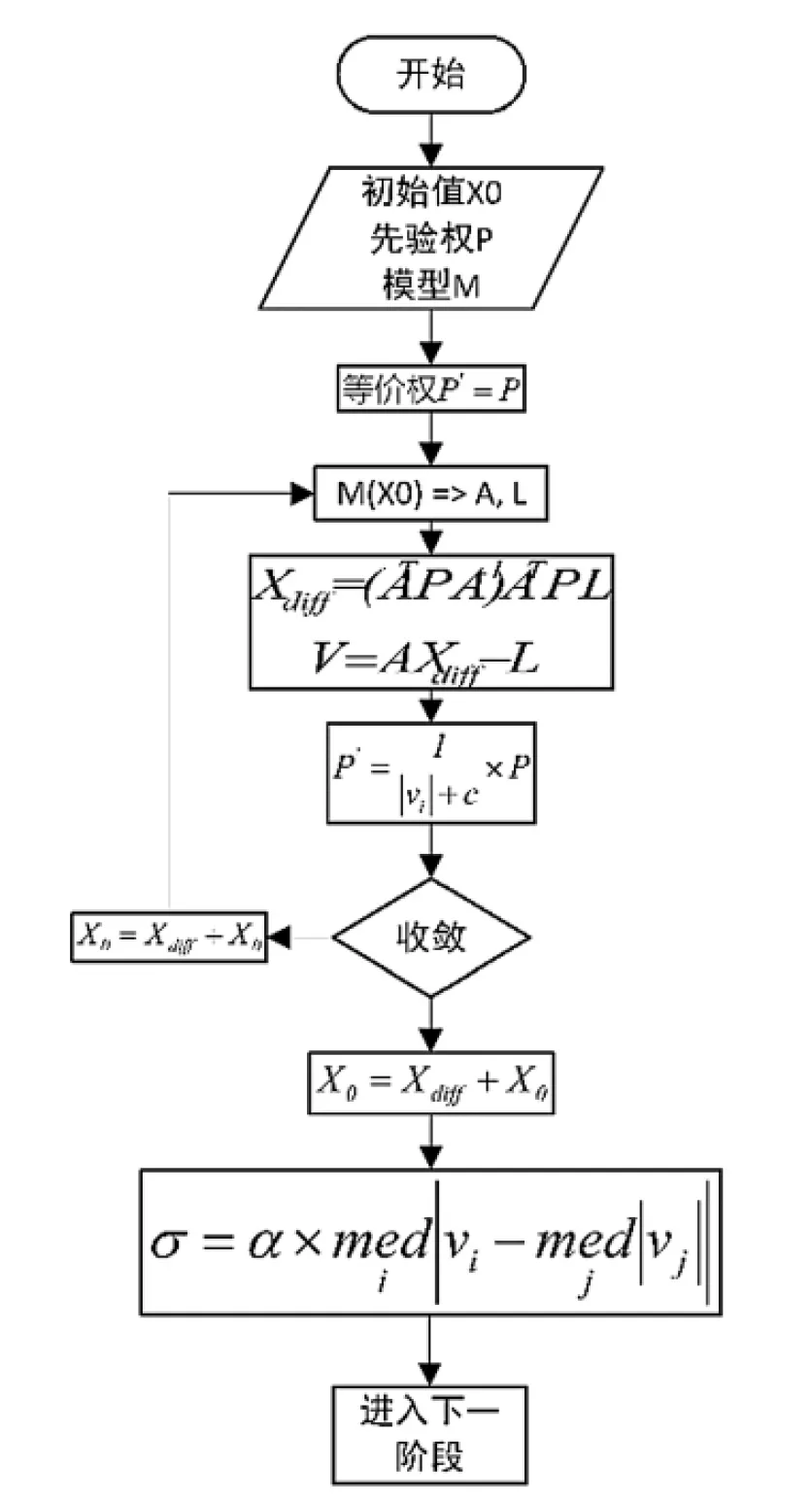
圖2 初值選取過程

3.2 粗差剔除階段

此階段的目標是使粗差充分暴露。一般通過選權迭代法將粗差的權重逐漸降低。可以選用IGG Ⅲ選權原則進行此階段的計算。計算過程如圖3所示。

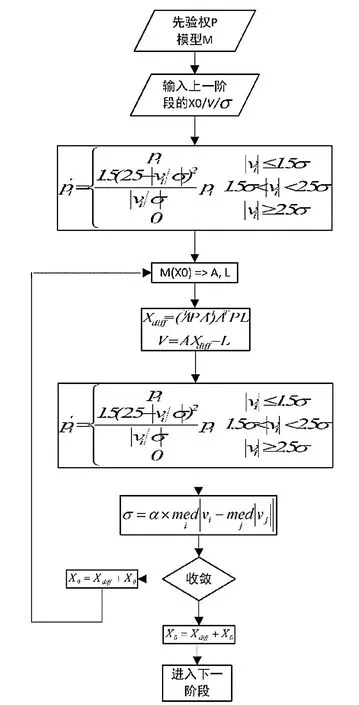
圖3 粗差剔除過程

3.3 最優(yōu)結果階段

此階段的目的是重新進行權矩陣評估,進行精度估計,得到最優(yōu)結果。過程如圖4所示。

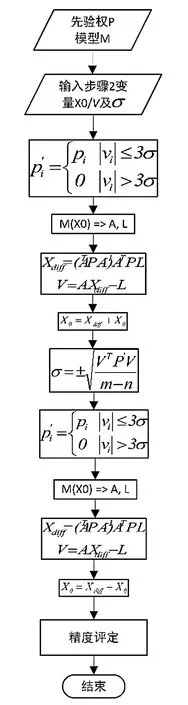
圖4 最優(yōu)結果階段過程

在實際測量數據中,一般只將數據分成準確數據和粗差數據兩部分。準確數據直接使用先驗權,粗差數據直接剔除。在這一步初廣泛接受的是萊因達準則,本文也使用萊因達準則。

4 圓心擬合

在工程測量數據處理過程中,可以將空間圓心擬合轉化為平面圓心擬合[7]。不失一般性,本文所述的圓心擬合都指平面圓心擬合。

以(x0,y0)為圓心,以R為半徑的圓可以表示為[8]:

(x-x0)2+(y-y0)2=R2

對于觀測點(xi,yi)列出其誤差方程為:

由圓的幾何意義可知,νi相當于點i與圓弧之間的距離。

根據文獻[2]將其線性化:

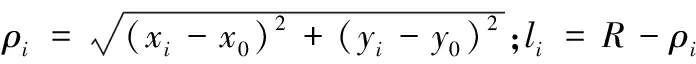
為了便于對比,引用文獻[9]圓柱體底部各點坐標數據,經三步平差方案擬合后,圓心為(49.986 2,60.012 8),半徑為0.430 4,單位權中誤差σ0=0.001 89。每點殘差及中誤差如表1所示。

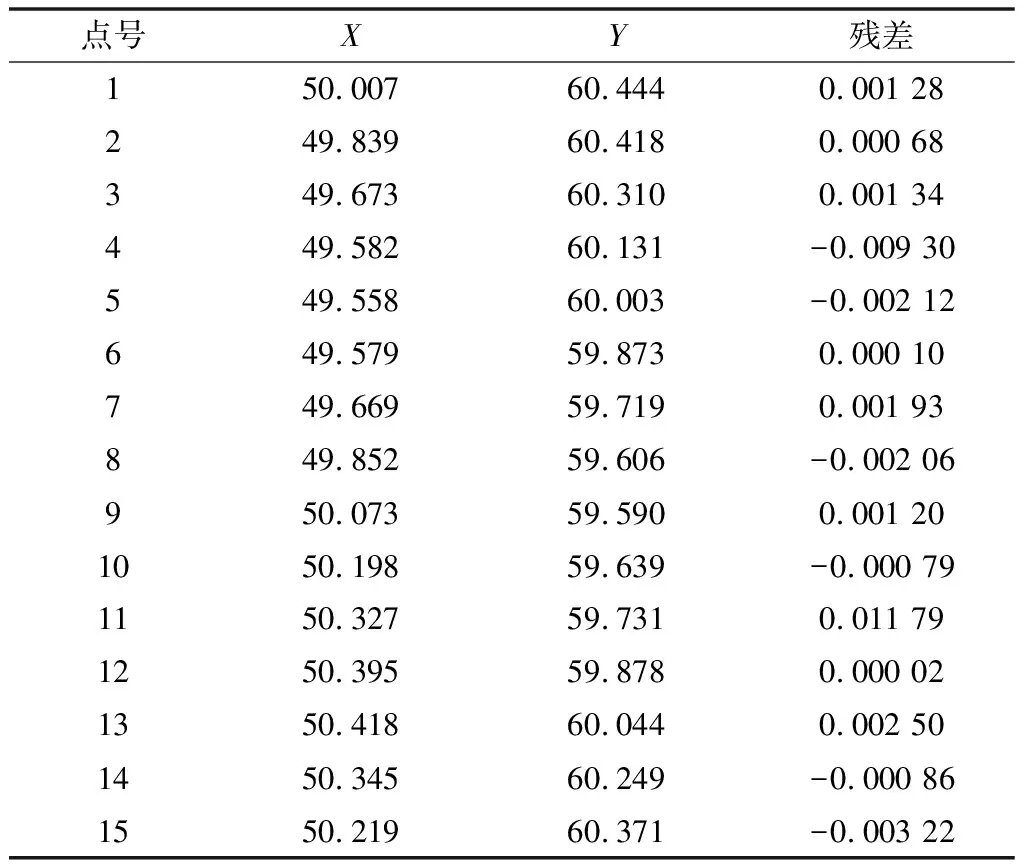
表1 圓柱體底部各點坐標 單位:m

與文獻[9]比較可以發(fā)現,本文方法與其穩(wěn)健估計的結果基本一致。都探測出了兩個粗差點(4號點、11號點)。

為了進一步測試三步平差方案的穩(wěn)定性及健壯性,使用程序自動生成圓心為(0,0),半徑為0.5的測試數據,并用三步平差方案進行擬合,以便對抗差方案進行分析。測量數據(xi,yi)生成方法如下:

αi=i×18+εi

ri=0.5+Δi

上式中:α為圓心到圓上的點與x軸的夾角,i∈[0,1,2,…,17];ε為從-4～+5的隨機整數;Δ為均值為0,標準差為0.001的,符合正態(tài)分布的隨機數。

為了模擬測量數據中存在的粗差,在上述的生成的測量數據中增加α為0～2π的隨機數,半徑r為0～4.996或0.504～1的隨機數的粗差。

用上述方法共生成60 000個測試數據(每一組用數據分別有1～30個粗差,共200組數據),對所有數據進行三步平差,結果統(tǒng)計如表2所示(只截取部分反映趨勢的結果)。

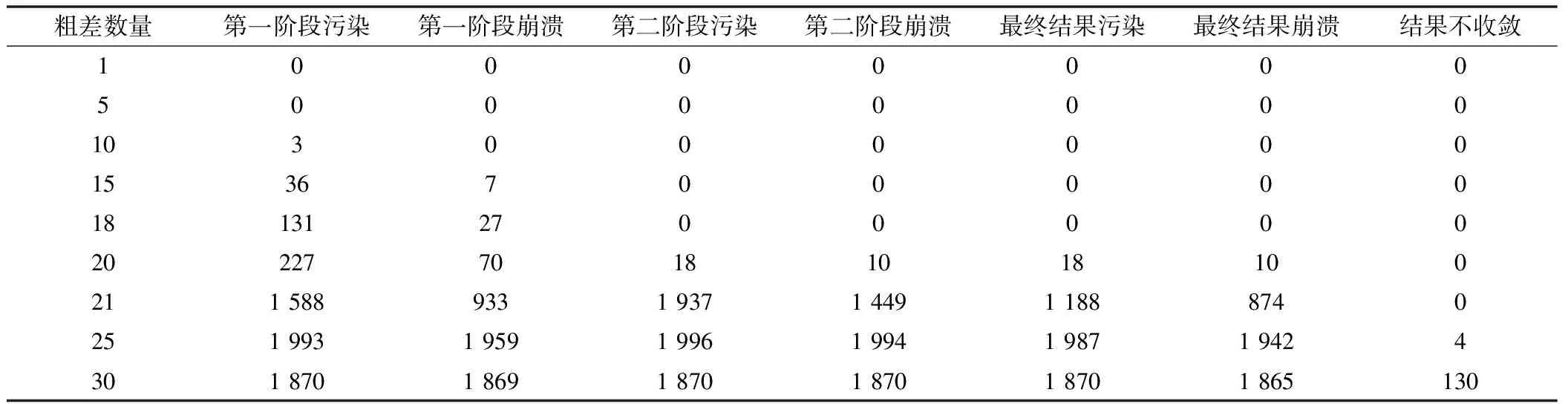
表2 結果統(tǒng)計

表2中第一階段污染表示其中誤差大于等于0.01,第一階段崩潰表示其中誤差大于等于0.02。第二階段污染表示其中誤差大于等于0.005,第二階段崩潰表示其中誤差大于等于0.01。結果污染表示其中誤差大于等于0.003,結果段崩潰表示其中誤差大于等于0.006。由上述結果可知,此方法的崩潰污染率接近50%(當污染率為50%時,崩潰率只有0.5%),但當污染率超過50%時,崩潰率迅速增加。隨著崩潰率的增加,會逐漸出現結果不收斂的情況。這是由于非線性模型的線性化是基于非線性函數的泰勒級數展開并忽略其高階無窮小。但由于第一階段的崩潰,無法提供給后續(xù)數據較好的初值,使舍去的高階無窮小量足以影響計算結果,導致算法不收斂。

5 結論

抗差最小二乘法能夠很好地減少測量數據中粗差的影響。如果使用三步抗差方案,在測量數據良好的情況下,崩潰污染率也高達50%,可以很好地應對工程測量數據處理中出現的各種問題。而且,經過第三階段的結果優(yōu)化,測量數據的精度也可以得到保證。