旋轉式能量回收裝置轉速測量方法研究*

袁任江,葉天壯,曲云飛,胡鑫超,焦 磊,2*

(1.浙江大學 海洋學院,浙江 舟山 316000;2.東海實驗室,浙江 舟山 316000)

0 引 言

隨著社會經濟的發展和人口的增長,全球水資源短缺問題日益突出[1],僅靠節約用水、提高水資源利用效率并不能完全解決該問題[2]。海水淡化技術在解決全球水資源危機方面發揮著日益重要的作用[3],其中反滲透海水淡化技術因工藝簡潔、裝置模塊化程度高、能耗低、維護便捷等優點,已逐漸成為極具應用前景和市場競爭力的主流技術[4]。

旋轉式能量回收裝置作為反滲透海水淡化系統中的新鮮海水的增壓元件,可將系統產水能耗從5.57 kW/m3降低至3 kW/m3以下,已成為反滲透海水淡化工程應用的三大關鍵裝備之一[5]。

旋轉式能量回收裝置中,無軸無外驅的轉子是裝置中最為關鍵的部件,也是唯一運動的部件[6]。整個裝置轉子的轉速是否正常直接反映了整臺裝置運轉狀態的好壞。正常運轉的裝置,其轉子轉速較高且穩定。當裝置出現異常時,轉子轉速過低,會導致反滲透海水淡化系統內壓力過高,以及發生高壓海水進料水流鹽分過高的故障,從而損壞裝置的反滲透膜[7]。然而,旋轉式能量回收裝置在運轉過程中類似一個“黑箱”,無法從外部直接測量到轉子的轉速。

在實驗室中,學者們可以在裝置外筒體上開設觀察窗,用激光轉速傳感器直接測量轉子轉速;但觀察窗需要承擔較高的壓力,長期運行存在較大的安全隱患,且須對外筒體和套筒進行專門設計加工。因此,這種測量轉子轉速的方式在實際工程中并不適用。

進行在線測量轉子轉速工作,對于判斷裝置運轉狀態,保障海水淡化系統長久穩定運行具有重要意義。近年來,眾多學者開展了與轉子轉速有關的研究。

XU E等人[8]研究了裝置尺寸參數對轉子沖擊動力矩與摩擦阻力矩的影響,建立了轉子轉速與裝置關鍵尺寸間的理論公式。孫揚平等人[9]建立了轉子所受動力矩、阻力矩與轉子轉速的關系式,并推導了轉速與系統流量間的理論公式。上述的2個理論公式可以為能量回收裝置的結構優化設計、操作條件的選取等提供理論參考。但是,在轉子實際運轉過程中,轉子的轉速會受到各種因素的影響,該系列理論還難以應用于實際轉子轉速的測量。

趙飛等人[10]利用仿真的方法,發現了端蓋內液體壓力脈動的主頻為轉子孔道的通過頻率,提出了通過測量壓力脈動頻率來獲知轉子轉速的方法。謝強等人[11]采用數值模擬方式,發現了壓力脈動在端蓋與轉子交界面最為明顯,隨著測點離交界面距離的增大,脈動量隨之減小。

因此,管道內的壓力脈動已經無法準確體現轉子轉速;而端蓋內的壓力脈動難以測量,還需在工程應用上對該方法進行探索。

在其他旋轉機械領域,有學者研究了利用振動信號測量轉速的方法,可以滿足無損、實時和準確測量轉速的要求[12,13]。

YANG Y等人[14]提出了一種參數化的時頻分析方法,用于分析變速旋轉機械的非平穩振動信號,并基于該方法提取了水輪機轉子在停機階段的瞬時頻率特征。張宇等人[15]使用快速傅立葉變換(fast Fourier transform,FFT)+補零算法和FFT+插值算法,優化了測量的壓縮機振動信號,提高了頻譜分辨率,提升了轉速測量的精度。

但以上研究都沒考慮噪聲對轉頻識別帶來的干擾。

常玉等人[16]提出了采用平均幅度差函數和差分閾值分段處理相結合的算法,以此來提取脫水階段振動信號對應的轉速,并對衰減段的奇異點進行了判斷和修正;其采用奇異點前后的均值代替奇異點的值,雖然該方法可以降低偏差,但是仍然丟失了真實數值。

過去,學者們在進行旋轉式能量回收裝置的研究過程中,較為注重裝置關鍵尺寸、系統流量、壓力脈動與轉子轉速之間的聯系,但沒有重視裝置振動與轉子轉速的關聯方面的研究。并且,旋轉式能量回收裝置的轉子“懸浮”在液體中并受到液力驅動,其振動的信號較為復雜,轉頻的倍頻信號會被噪聲所掩蓋,對信號直接進行時頻分析所獲得的結果,已經不能準確地體現轉子的轉速信息。

為了準確地測量轉子的轉速,筆者對旋轉式能量回收裝置振動頻率與轉子轉頻進行分析,提出一種基于振動信號的旋轉式能量回收裝置轉子轉速測量方法,即通過小波變換、信號包絡解調、帶通濾波處理等過程,降低噪聲的干擾;然后,提取振動主頻,依據振動頻率與轉頻的關系計算轉子轉速;最后,通過實驗驗證該方法在裝置平穩以及非平穩運轉狀態下測量轉子轉速的準確率。

1 裝置振動與轉速數據的采集與分析

1.1 旋轉式能量回收裝置主要結構

旋轉式能量回收裝置可以將被反滲透膜截留的高壓廢水的壓力直接傳遞給新鮮海水,從而減少將新鮮海水加壓至膜前壓力所需的能耗,提高系統的能效。

旋轉式能量回收裝置的主要結構如圖1所示。

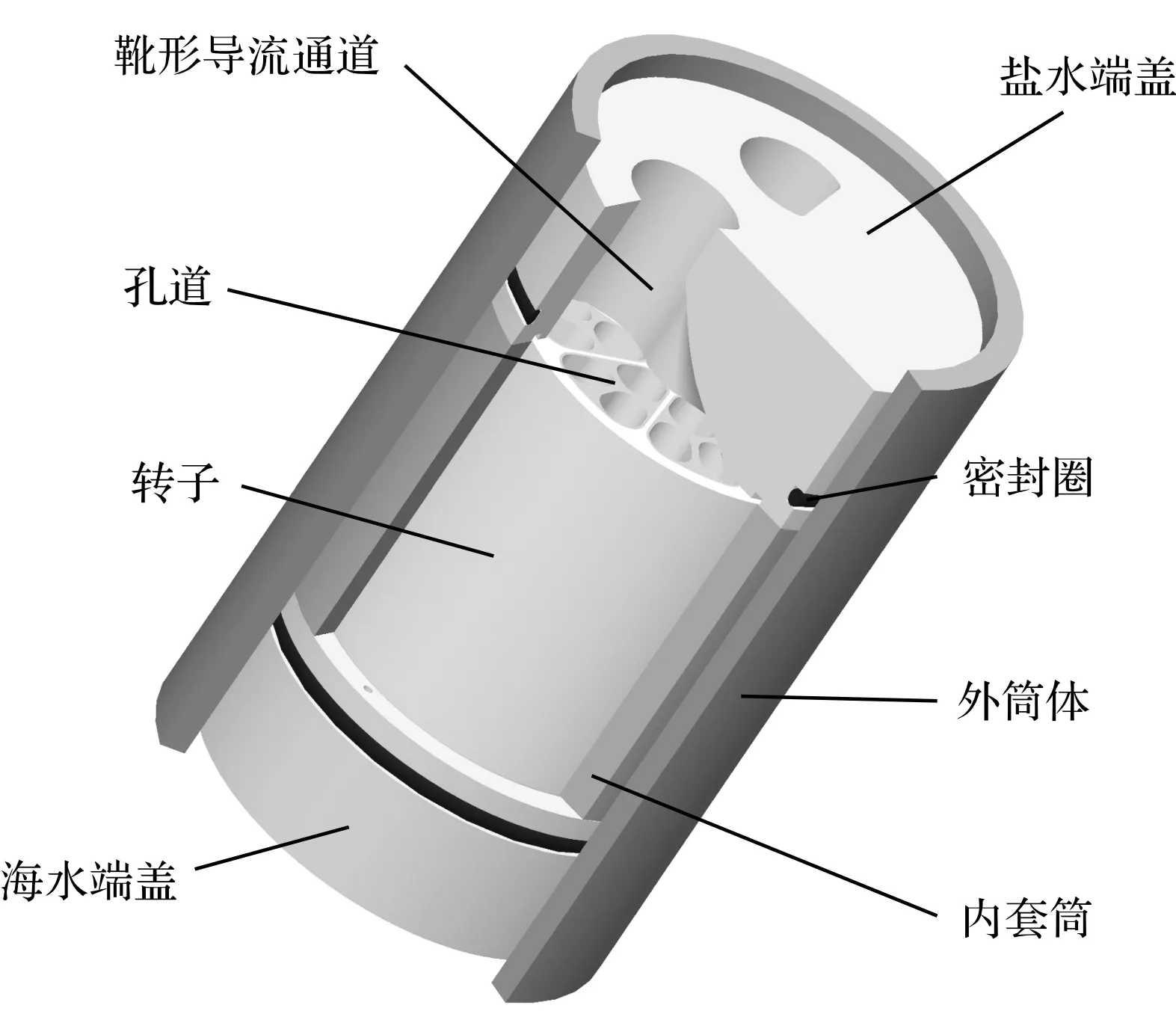
圖1 旋轉式能量回收裝置主要結構示意圖

從圖1可以看出:裝置主要由鹽水端蓋、海水端蓋、轉子、內套筒和外筒體,五部分構成。

裝置工作時,高壓鹽水、新鮮海水分別從鹽水端蓋、海水端蓋的靴形流道流入,水流通過靴形流道導流具有一定的切向速度,沖擊轉子孔道側壁驅動轉子旋轉。轉子由雙層孔道構成,內層孔道8個,外層孔道16個,分為8個分區,孔道與孔道之間被完全隔離。轉子與內套筒以及端蓋之間存在微小間隙,裝置運轉時,海水會充滿間隙并形成一層水膜,起到潤滑與支撐的作用。內套筒與端蓋通過定位銷定位,端蓋與外筒體間配有密封圈。

1.2 實驗裝置及實驗流程

實驗過程中,筆者需要同步采集能量回收裝置振動與轉速數據。

實驗裝置及振動、轉速測量儀器如圖2所示。

圖2 實驗裝置及振動、轉速測量儀器

圖2中,課題組自主研制的單臺實型旋轉式能量回收裝置為該實驗的實驗對象,其外筒體為316 L不銹鋼,便于在筒身開設觀察窗。

筆者采用專用耦合劑將三軸加速度傳感器(PCB 356A15)固定在旋轉式能量回收轉置外筒體中部,測取外筒體徑向的振動加速度信號;將激光轉速傳感器(Monarch ROLS-P)布置在距外筒體0.3 m遠處(激光發射器發出的激光透過外筒體開設的玻璃觀察窗照射在能量回收裝置轉子上,轉子上粘貼有反光帶以反射激光,轉速傳感器接收反射激光獲得轉子的轉速信息);使用數據采集儀(LMS SCADAS Mobile)同時獲取振動傳感器和轉速傳感器的信號,采樣頻率為12 800 Hz。

另外,筆者采用電磁流量計(Rosemount 8732E型)和壓力變送器(Keller PA-21Y),將其安置在與流道連接的管道處,分別測量系統流量和高壓進口液體壓力。

實驗中,為保證玻璃觀察窗的安全性,筆者設置高壓進口壓力為2 MPa,流量調節范圍設置為50 m3/h～80 m3/h,每隔5 m3/h為一個實驗工況。

流量調節穩定后,觀察轉子轉速變化情況,待轉速相對穩定后,再采集振動信號與轉速數據。雖然此時轉速與振動仍是非平穩的時變信號,但在較短的時間間隔內可以認為其基本平穩;并且考慮到能量回收裝置轉子轉頻僅為10 Hz左右,所以頻率分辨率不宜低于1 Hz,否則不便于準確發現振動頻率與轉頻之間的關系。

因此,經綜合考慮,筆者將采樣時間設定為1 s。

1.3 振動信號與轉速信號數據分析

高壓進口壓力為2 MPa工況下,不同流量下轉速、轉頻數據和振動加速度的均方根(root mean square, RMS)值如表1所示。

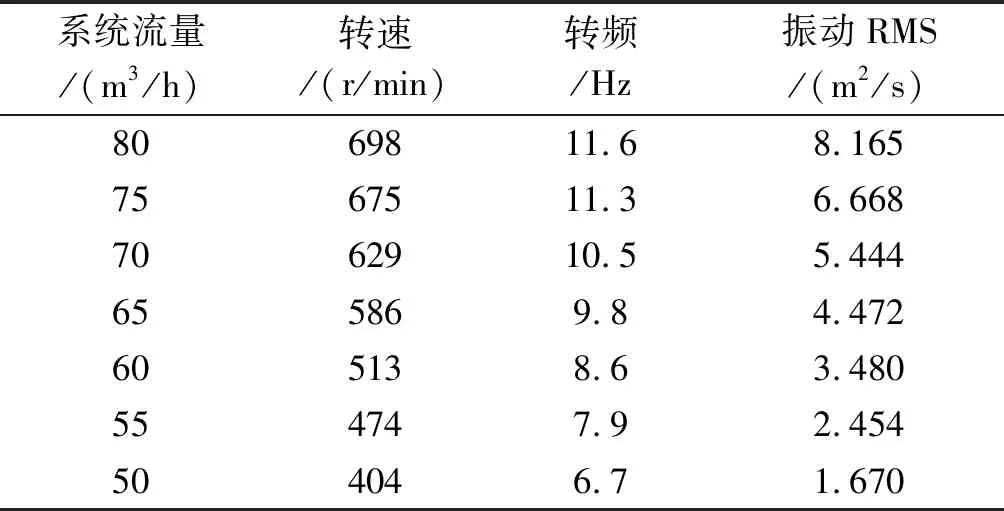
表1 不同流量下轉速與振動RMS

表1中的振動RMS值用以表征振動信號的平均有效能量,其計算公式為[17]:

(1)

式中:k為計算區間的總樣本點數,此處為12 800;Xi為振動信號的測量值,m2/s。

從表1中可以看出:隨著系統流量從50 m3/h升高至80 m3/h,轉子轉速由404 r/min升高至698 r/min,同時振動RMS值從1.670 m2/s升高至8.165 m2/s,轉速越快,振動能量也越大。

高壓進口壓力為2 MPa,流量為70 m3/h工況下,徑向振動加速度頻譜如圖3所示。

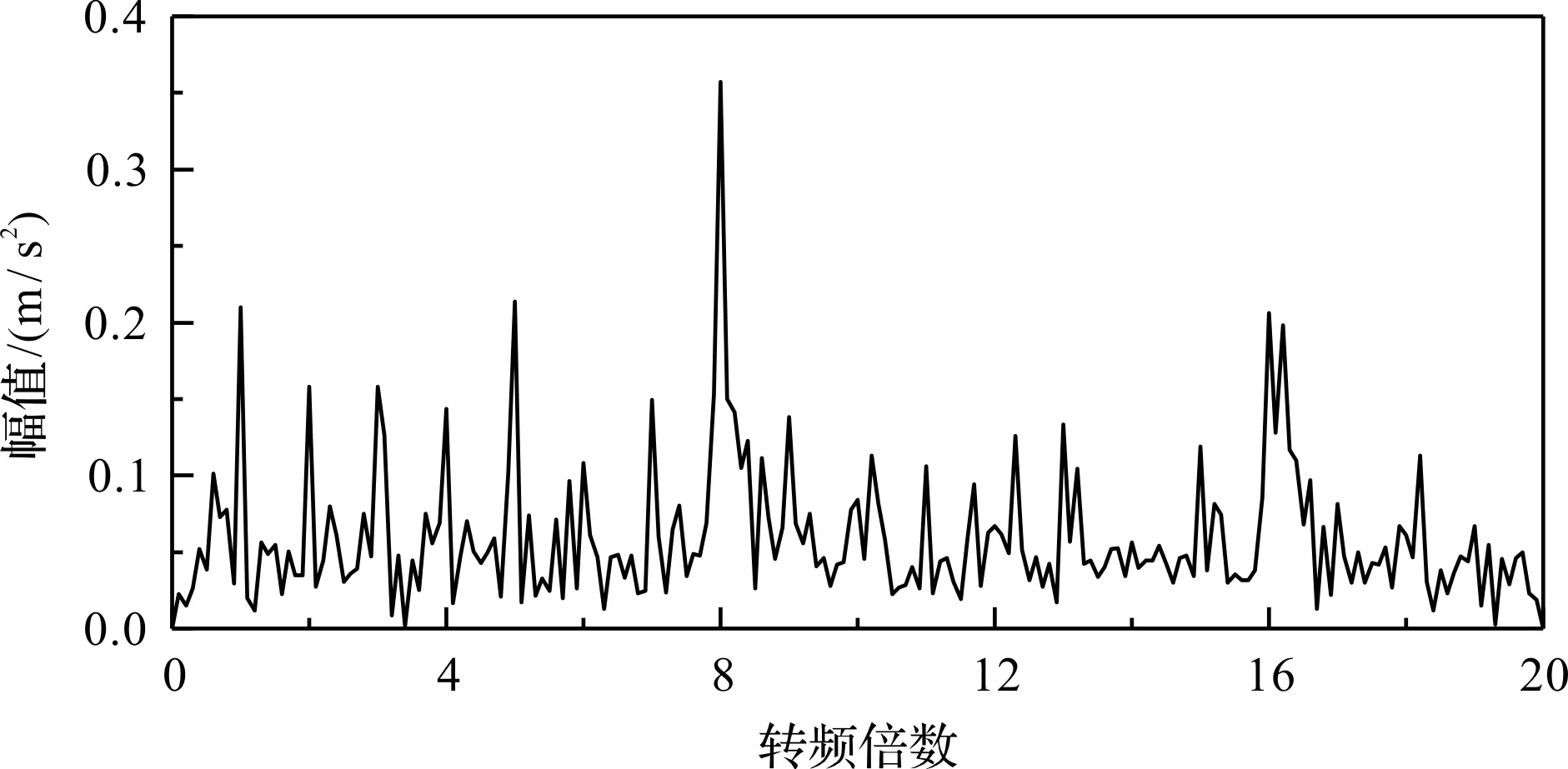
圖3 裝置振動加速度頻譜

圖3中,工況所對應的轉子旋轉速度為629 r/min,即轉頻為10.5 Hz,圖中縱軸表示幅值,橫軸表示轉頻倍數。此處定義轉頻倍數的計算公式為:

(2)

式中:N為轉頻倍數;f為振動頻率,Hz;n為轉子轉速,r/min;fn為轉子轉頻,Hz。

從圖3可以看出:振動的主要頻率為8倍轉頻,其中8倍轉頻對應著內圈的8個孔道從高壓區進入封閉區的頻率。轉子在水流的驅動下旋轉,轉子孔道進入封閉區的瞬間,進出水流受阻產生類似水錘效益,形成壓力脈動,液體壓力傳遞到外筒體,引起筒體的振動響應,因此,頻譜中8倍轉頻處出現較大幅值。

同樣,轉子外圈有16個孔道,外圈孔道進入封閉區的頻率對應著16倍轉頻,但其幅值低于8倍轉頻。除此之外,頻譜中轉子1倍轉頻及其諧波頻率也有明顯幅值。

高壓進口壓力為2 MPa,流量為50 m3/h～80 m3/h工況下,裝置的振動加速度頻譜如圖4所示。

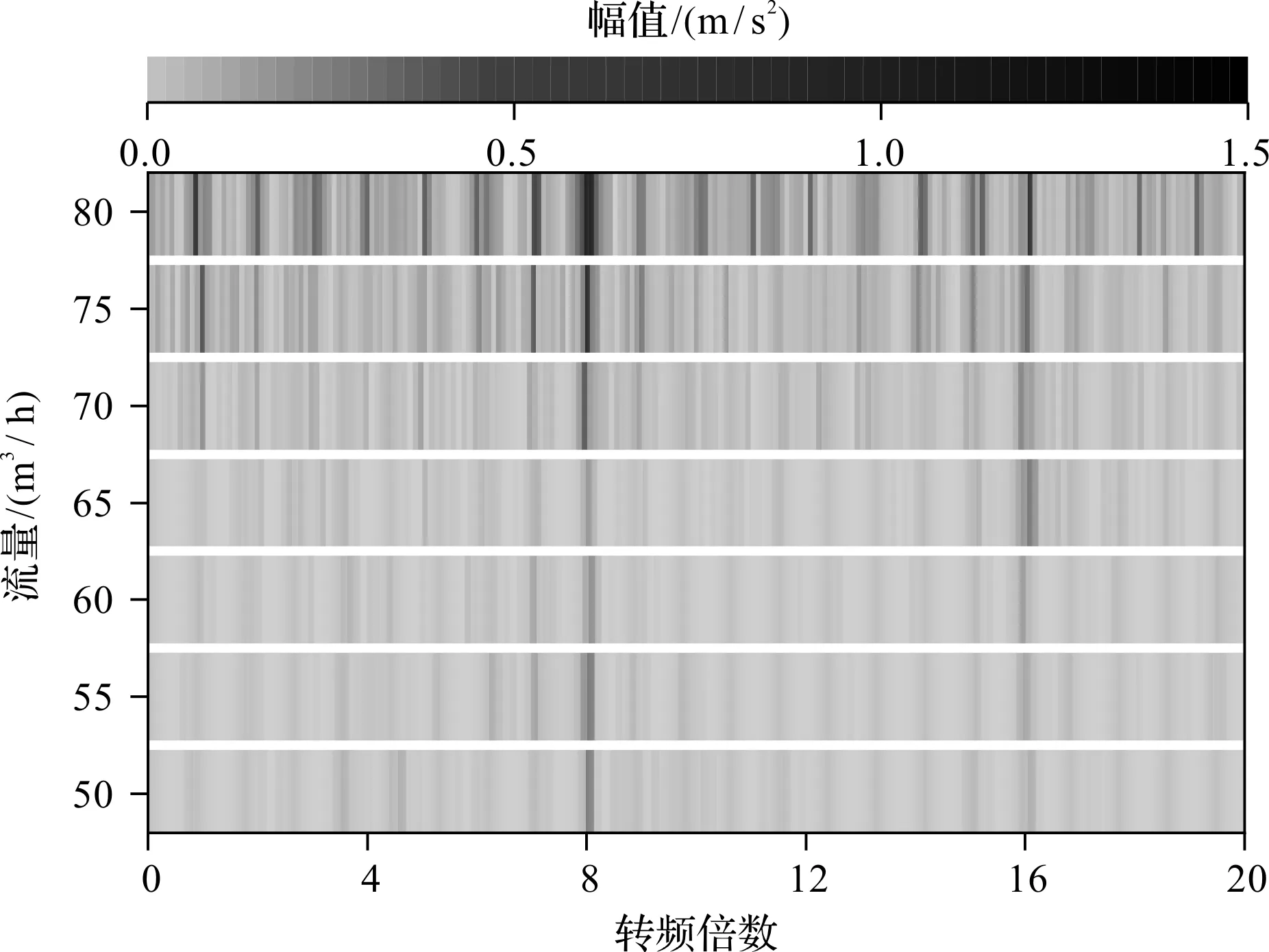
圖4 不同流量下裝置振動加速度頻譜

從圖4可以看出:不同的流量下,8倍轉頻都具有較高的幅值,其次為16倍轉頻。當流量小于65 m3/h,轉子轉速較低時,轉子1倍轉頻及其諧波頻率不明顯,可以推測轉子1倍轉頻振動的出現與轉子旋轉不平衡有關。

通過上述分析,可以得到轉子轉速、振動主頻與轉換倍數之間的對應關系為:

(3)

式中:n為轉子轉速,r/min;f0為振動主頻,Hz;i為轉換系數。

對于旋轉式能量回收裝置,筆者可以通過識別振動主頻并進行倍數轉換,得到轉子轉速。

2 裝置振動信號處理與轉頻計算

旋轉式能量回收裝置的振動信號中含有與轉頻相關的信息,但流量與壓力急劇變化會造成振動信號基線漂移,轉頻的倍頻信號也會被高頻噪聲所掩蓋,并且不同轉頻倍頻之間也會相互干擾,因此,無法通過簡單的時頻分析從振動信號中準確獲知轉子轉頻的倍頻。

針對以上問題,筆者通過分析實際采集的振動信號中的干擾成分,提出了旋轉式能量回收裝置振動信號處理與轉速計算流程,如圖5所示。

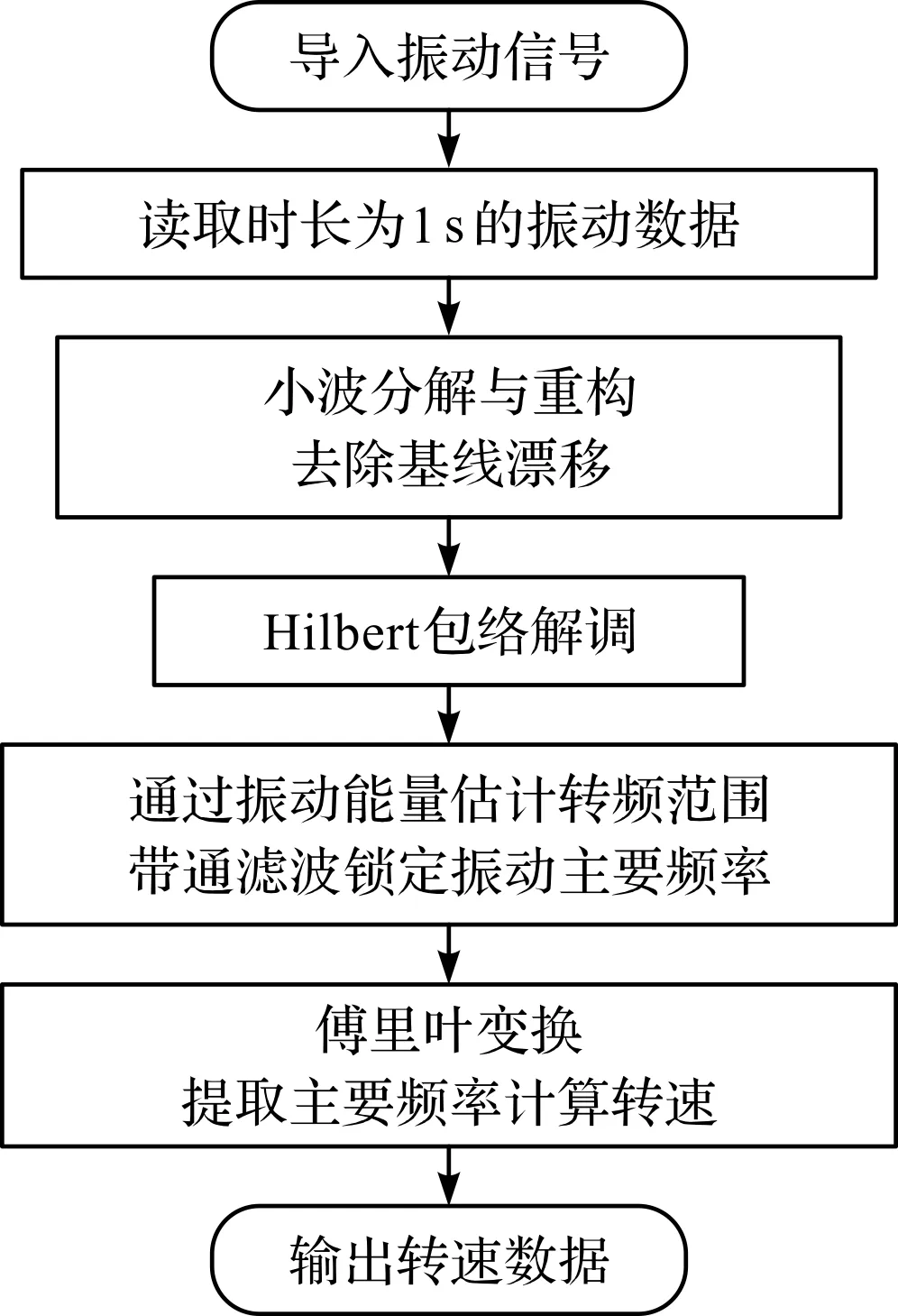
圖5 旋轉式能量回收裝置振動信號處理與轉速計算

從圖5可以看出:每次計算需要讀取時長為1 s的振動數據,并對數據進行包括小波變換去除基線漂移、Hilbert包絡解調、估計頻率范圍、傅里葉變換等處理工作。

2.1 消除基線漂移

旋轉式能量回收裝置實測的振動信號中存在基線漂移干擾。能量回收裝置運轉穩定時,外筒體振動信號數據關于坐標軸對稱良好。當裝置的進出口流量與壓力出現波動,或者裝置中存在異物影響轉子穩定旋轉時,振動信號就會出現基線漂移,影響后續的信號處理。

裝置基線漂移振動信號及轉速如圖6所示。

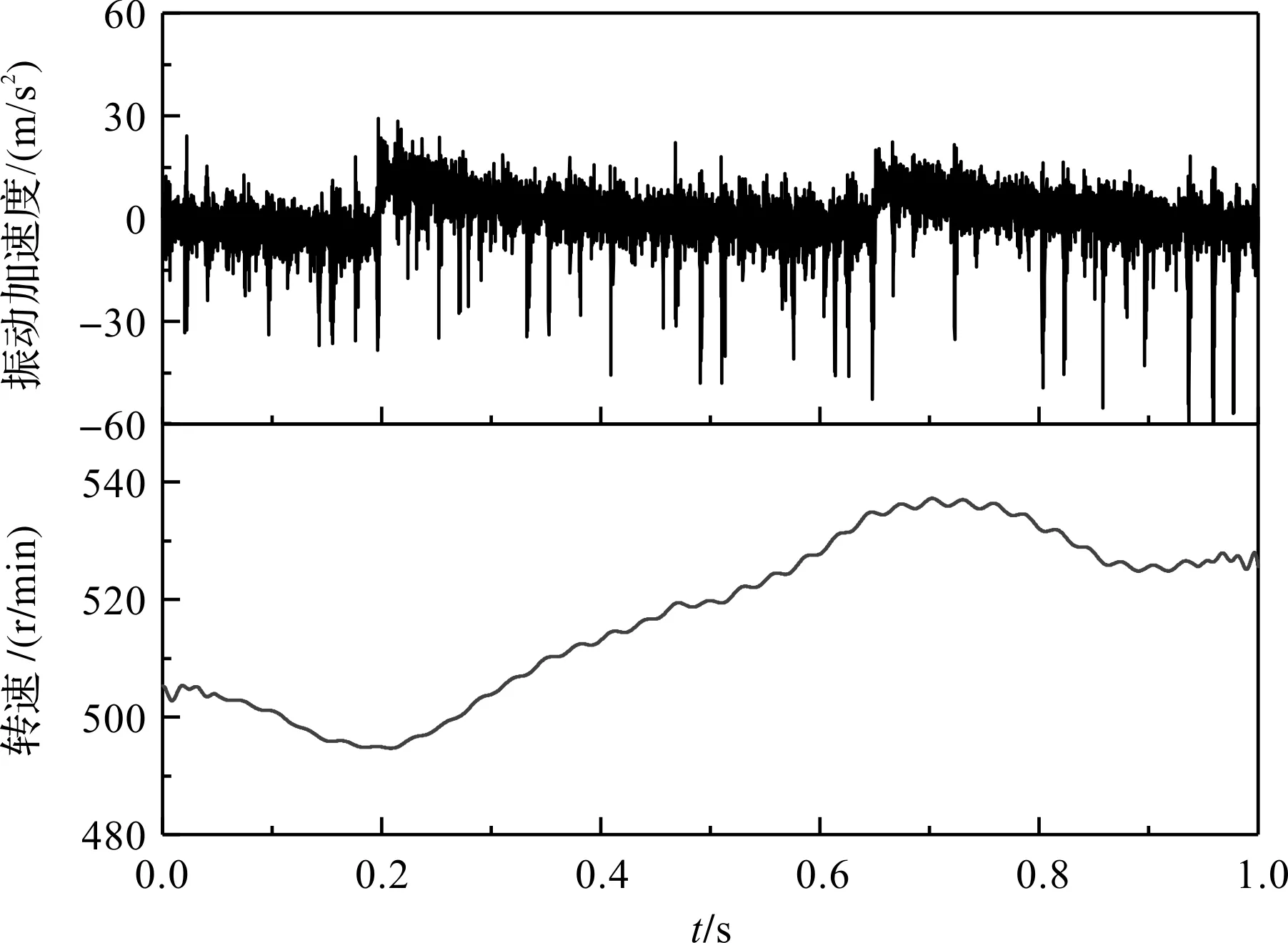
圖6 裝置基線漂移振動信號及轉速

在圖6中,振動加速度除了高頻振蕩,還有低頻的基線漂移。消除基線漂移噪聲實際上是抑制信號中的無用部分,恢復信號中的有用部分的過程。小波變換具有“時間-頻率”窗口隨頻率改變的特點,這一特點使得小波變換能自動適應信號分析的要求[18]。

對于能量有限的函數f(t)∈L2(R),小波變換的表達式為[19]:

(4)

式中:Wf(a,b)為小波變換系數;a為尺度因子;b為平移因子;ψ(t)為小波母函數。

小波變換能把振動信號在不同尺度上進行多分辨率分解。

小波分解算法如圖7所示。

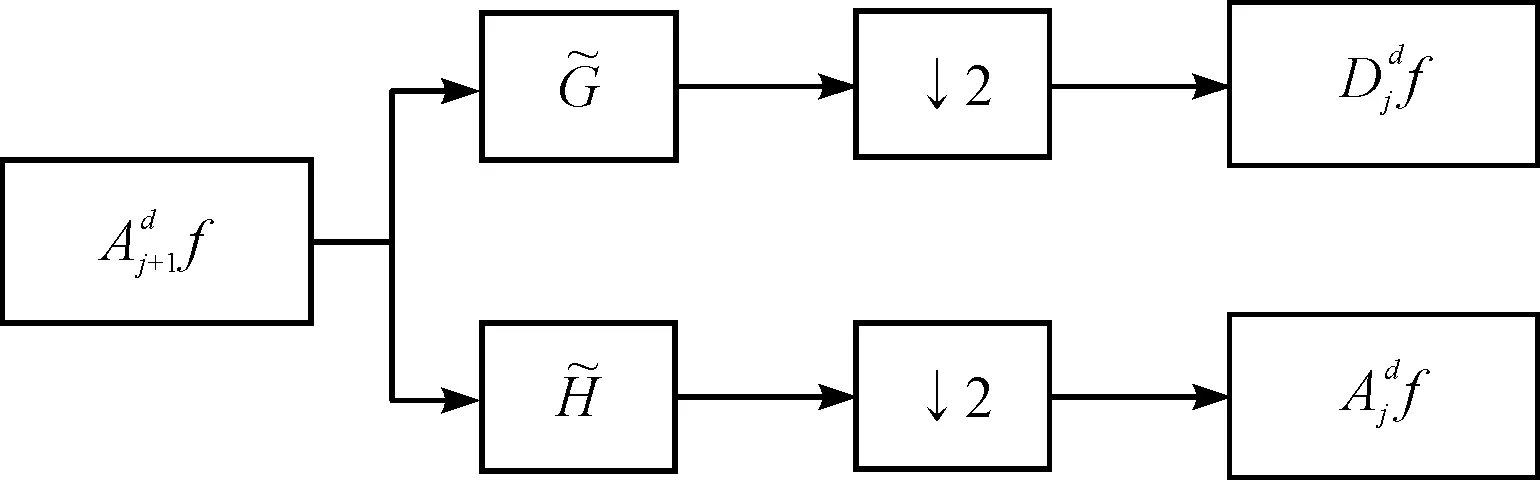
圖7 小波分解算法

(5)

對應的重構算法為:

(6)

筆者利用小波分解與重構去除基線漂移時,需要選擇恰當的小波分解層數。

不同分解層數得到的基線信號如圖8所示。

從圖8可以看出:分解層數為6層時,基線信號中會夾雜部分有用的低頻信號,此時對振動信號重構會導致這部分信息丟失;分解層數越高,基線信號會越平坦,當分解層數為8時,基線信號起伏不明顯,不能很好地逼近漂移噪聲;當分解層數選擇為7時,基線信號與漂移噪聲信號形狀接近。

筆者選用sym8小波函數,對旋轉式能量回收裝置振動信號進行多尺度分解,分解水平為7,得到與振動基線漂移噪聲充分逼近的低頻部分信號,將此逼近信號去除,再將分解得到的高頻部分信號進行重構,獲得平穩的振動信號。

基線校正后的振動信號如圖9所示。

從圖9可以看出:基線校正可以達到濾除振動信號中基線漂移的目的,同時保留包括轉頻信息在內的中頻和高頻部分的信號。

2.2 信號包絡解調

與轉頻相關的低頻信號會淹沒在高頻振動和噪聲中,難以分辨,通過Hilbert包絡解調,可以極大地提高重要數據在信號中的占比[20]。

Hilbert包絡解調法是一種常用的信號包絡提取方法。Hilbert變換巧妙地應用解析表達式中的實部與虛部的正弦和余弦關系,定義出任意時刻的瞬時頻率、瞬時相位及瞬時幅度,從而能更有效地、真實地獲取信號中所含的信息,有利于分析短時間的能量回收裝置振動信號。

(7)

(8)

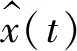
(9)

筆者對包絡信號進行傅里葉變換后,可做出原始振動信號x(t)的包絡解調譜。

包絡解調前后的振動信號如圖10所示。

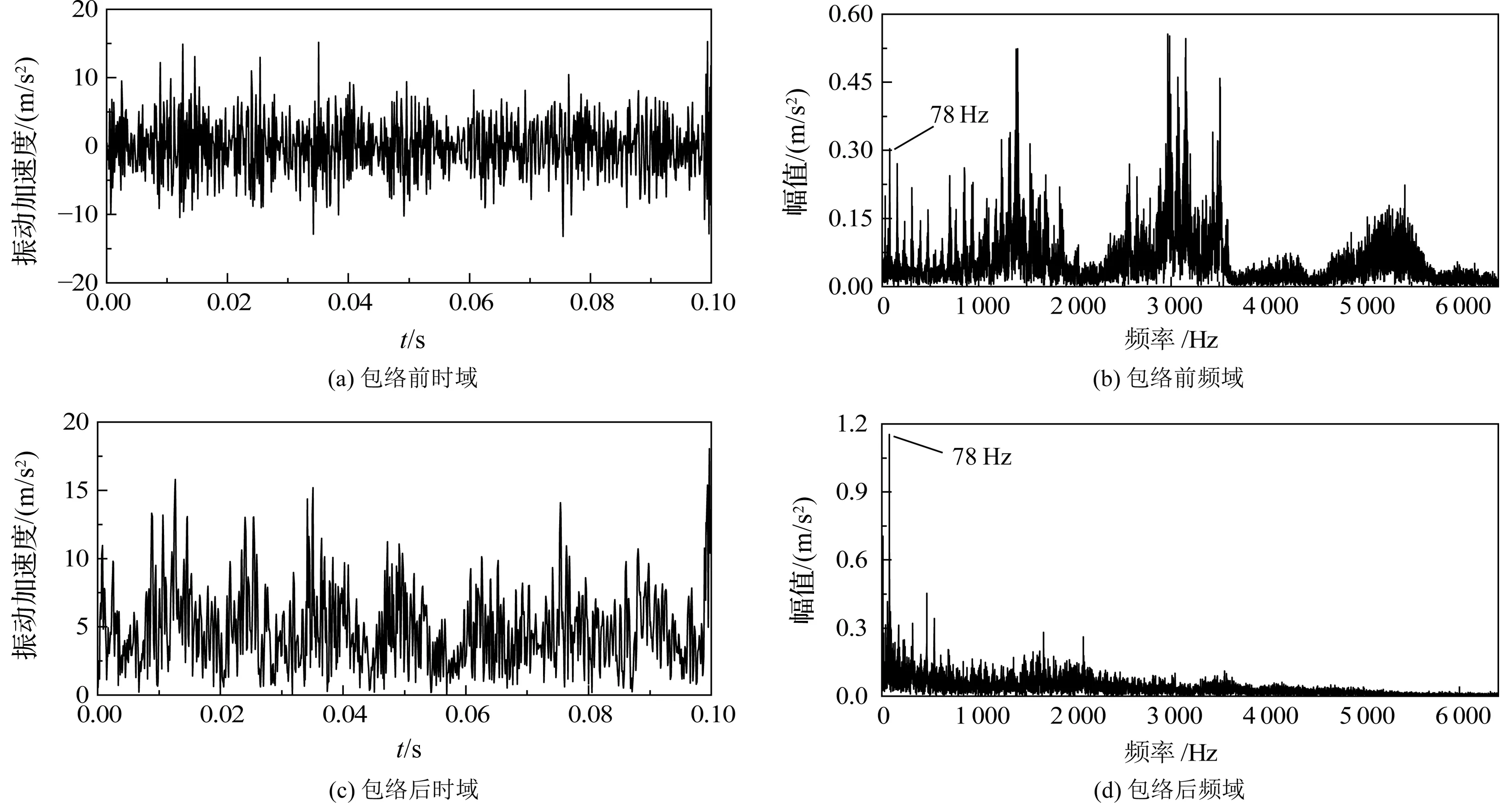
圖10 包絡解調前后的振動信號

由圖10(a)和圖10(b)可以看出:包絡前的振動加速度時域信號周期性不明顯。振動頻譜中的78 Hz為8倍轉頻對應的振動頻率;采集的旋轉式能量回收裝置的振動信號包含高頻振蕩信號,振動頻率在1 400 Hz與3 000 Hz附近的高頻部分存在明顯的峰,并且峰的附近出現間隔78 Hz的調制邊頻帶,說明8倍轉頻信號被高頻信號所調制。

從圖10(c)和圖10(d)可以看出:經過包絡解調之后,原信號的主要周期特征都很好地突顯出來。頻譜中,原本1 400 Hz與3 000 Hz處的高頻信號得到抑制,包絡解調極大地提高了8倍轉頻信號的占比。

高壓進口壓力為2 MPa,不同流量工況下,經過包絡解調處理后的振動加速度頻譜如圖11所示。

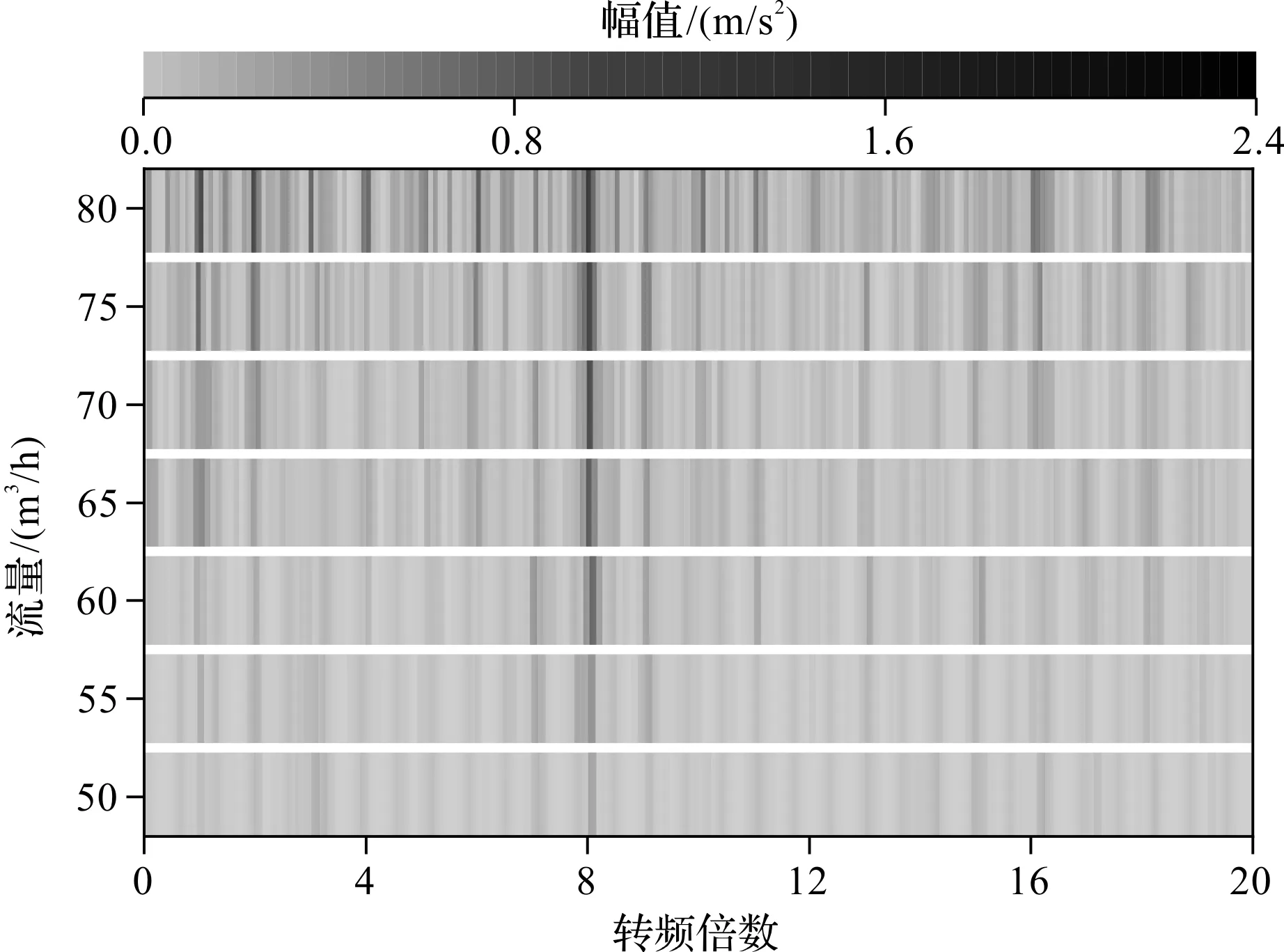
圖11 不同流量下解調處理后的振動頻譜

對比圖4和圖11可以看出:經過解調處理后,16倍轉頻不再明顯,在流量為65 m3/h的這組實驗中,16倍轉頻對應的峰已難以識別,無法通過識別振動信號中的16倍轉頻來計算轉子轉頻;當流量較大、轉速較高時,1倍轉頻的峰值較為清晰,但1倍轉頻在低轉速下幅值較低,并且在相同的頻率分辨率下,1倍轉頻計算得到的轉子轉頻的精度最差;相較之下8倍轉頻在多數工況中都可以尋找到8倍轉頻對應的峰,顯然通過識別信號中的8倍轉頻來計算轉子轉頻會更加穩定且精準。

2.3 通過振動能量估計轉頻范圍

筆者經大量的實驗發現,多數情況經過包絡解調處理后的振動頻譜的峰值頻率為轉頻的8倍(圖11);但在一些時刻,1倍或16倍轉頻的幅值會比8倍轉頻幅值更高。

帶通濾波處理前后的振動頻譜如圖12所示。

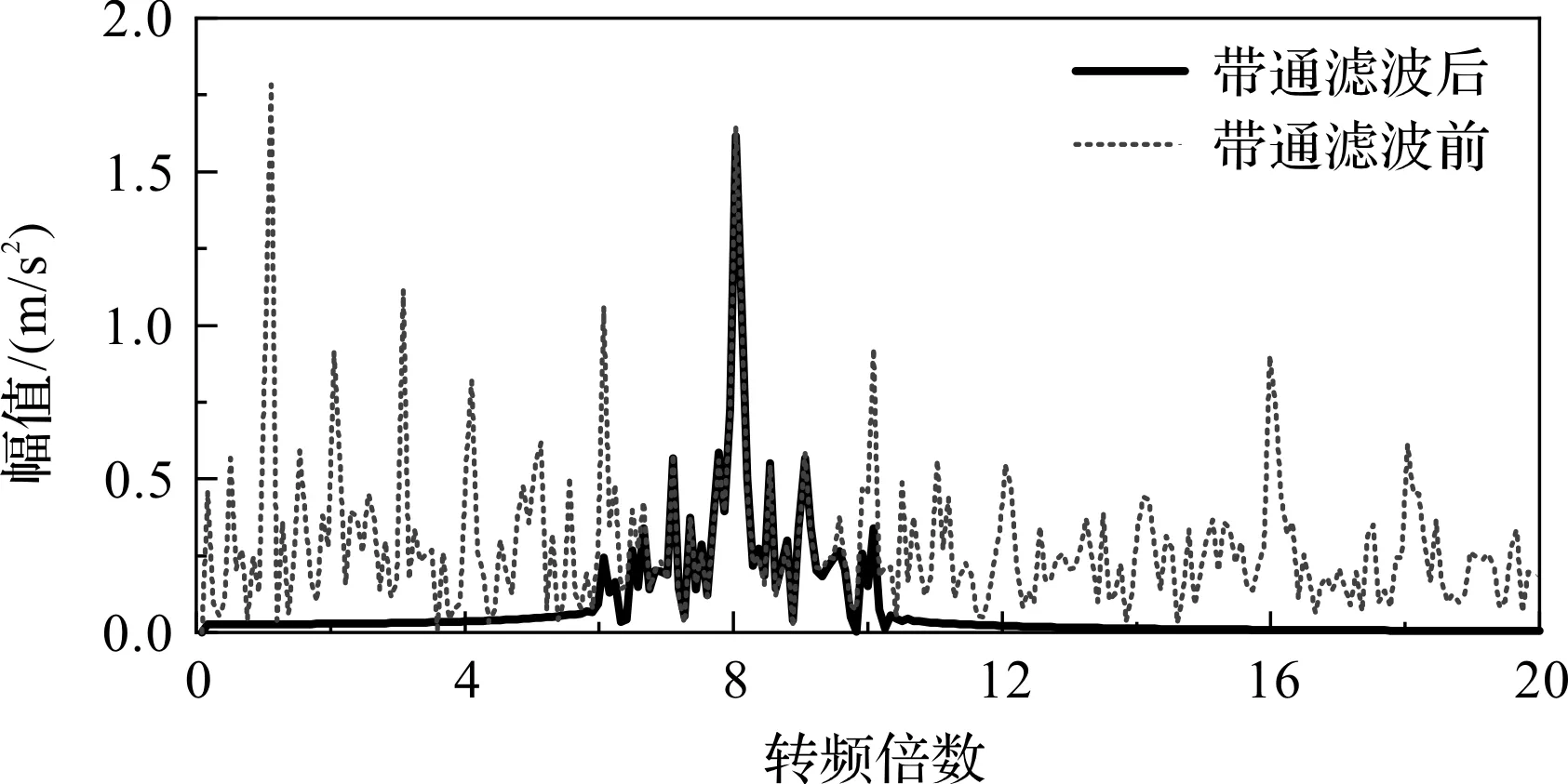
圖12 帶通濾波處理前后的振動頻譜

圖12中,虛線為帶通濾波處理前的振動頻譜,可以看出1倍轉頻的幅值要高于8倍轉頻。而計算轉子轉速需要準確提取8倍轉頻,因此,需要估計8倍轉頻的范圍,并進行帶通濾波處理,將可能造成干擾的頻段濾除。

筆者將前述實驗中測得的振動RMS值以及RMS值對應的轉速數據進行擬合,得到RMS值與轉頻的關系式為:

8×fn=-0.006 43×RMS2+1.24×RMS+35.2

(10)

式中:fn為轉子轉頻,Hz;RMS為振動均方根值,m2/s。

RMS值與轉速數據的擬合公式的調整后相關系數R2為0.991。但振動RMS容易受到眾多因素的影響,通過擬合公式計算得到的轉速并不完全準確,但可以用于估計轉頻范圍。筆者將公式計算的值的1.25倍作為估計轉頻范圍上限,0.75倍作為估計轉頻范圍下限,從而確定估計的轉頻范圍。

不同流量下實測轉速與通過RMS估計的轉速范圍,如圖13所示。

圖13 不同流量下實測轉速與通過RMS估計的轉速范圍

從圖13可以看出:估計的轉頻范圍可以將各工況下的實測8倍轉頻包括在估計轉速范圍內,有效地將1倍轉頻和16倍轉頻排除在外;之后采用帶通濾波的方法對振動數據進行處理,僅保留估計轉頻上、下限之間的頻率,可以得到去除其余倍頻干擾的振動信號。

圖12中,實線為帶通濾波處理后的振動頻譜,1倍轉頻和16倍轉頻信號被濾除后,最大幅值對應的振動頻率即為8倍轉頻,對此頻率進行換算就可以得到此刻的轉子轉頻。

3 轉速測量實驗驗證

為了對該轉速測量方法的準確性進行驗證,筆者在實驗平臺上對此進行實驗。實驗對象為前述能量回收裝置。其中,外筒體振動信號與轉子轉速的采集方式與之前所述一致,采樣頻率為12 800 Hz。

首先,基于振動信號的轉速測量方法的準確性,檢驗裝置平穩運轉狀態。筆者將高壓進口壓力設置為2 MPa,緩慢提高系統流量,同時觀察轉子轉速,當轉子轉速在400 r/min左右時暫停加大流量,待轉速穩定后進行數據采集。為了保證數據采集與處理的穩定性和可靠性,連續采集20段時長為1 s的轉子轉速與振動數據。依照上述步驟,筆者分別采集轉子500 r/min、600 r/min、700 r/min左右的轉速與振動數據。

筆者將激光轉速傳感器采集的轉速記作直接測量轉速,通過振動信號利用算法計算得到的轉速記作間接測量轉速。

誤差率的計算公式為:

(11)

式中:E為誤差率;nV為間接測量的轉速,r/min;nT為直接測量的轉速,r/min。

旋轉式能量回收裝置平穩運轉狀態下,轉子直接測量轉速和間接測量轉速結果如表2所示。

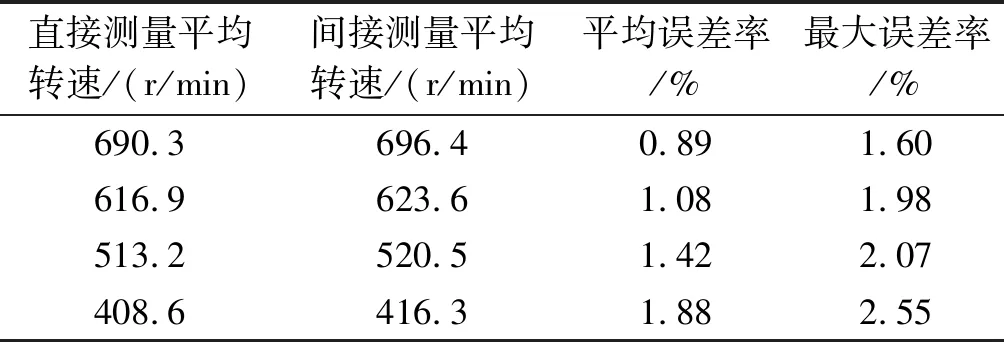
表2 平穩狀態下轉速測量實驗結果

從表2可以看出:在不同速度下,直接測量轉速與間接測量轉速的差值在6.1 r/min～7.7 r/min之間;平均誤差率小于1.88%,最大誤差率小于2.55%。

筆者采用連續改變流量的方式,使轉子處于非平穩運轉的狀態,以此檢驗該方法在非平穩狀態下的準確性。

非平穩狀態下轉速測量實驗結果如圖14所示。

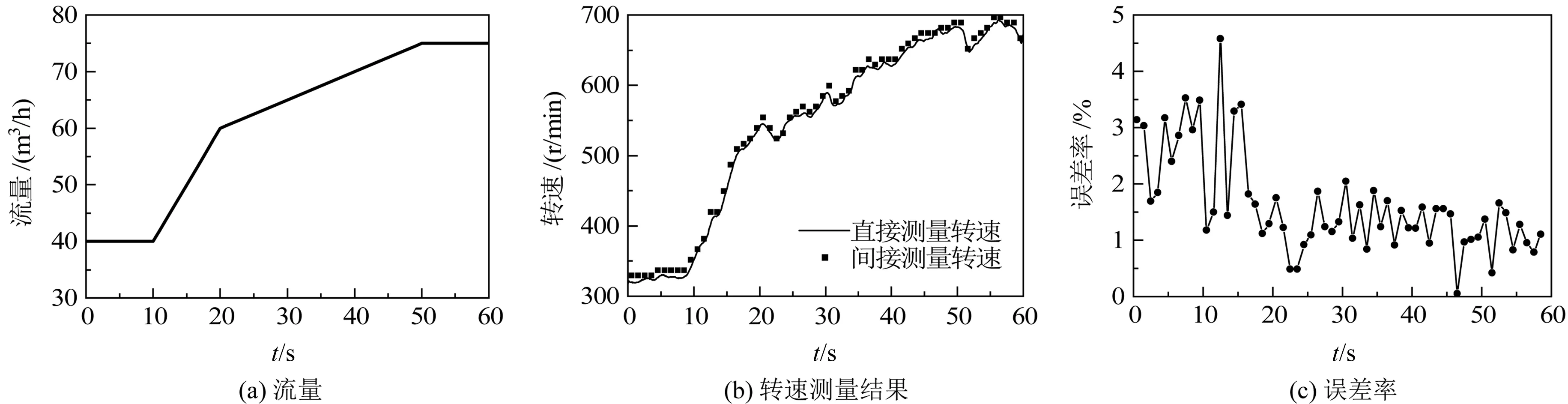
圖14 非平穩狀態轉速測量實驗

從圖14可以看出:系統流量在1 min內從40 m3/h升高至75 m3/h,轉速從320 r/min左右升高至680 r/min左右。間接測量的轉速與直接測量的轉速基本吻合,可以很好地反映運轉狀態。其中,最大誤差率為4.58%,發生在第13 s,1 min的平均誤差率為1.61%。

實驗結果表明:相較于平穩狀態,轉速測量準確性在非平穩狀態下有所下降,尤其是當轉速急劇變化時,此時的振動信號周期性較弱,振動主頻與實際轉速的8倍頻偏差增大,因而測量轉速誤差增大。

4 結束語

為了研究海水淡化旋轉式能量回收裝置轉速的測量方法,筆者通過實驗分析了裝置的振動頻率與轉子轉頻之間的關系,在此基礎上,提出了一種基于振動信號的轉子轉速間接測量方法。

首先,利用小波變換去除了基線漂移的干擾;其次,采用信號包絡解調突顯了轉頻信息,以及通過振動能量估計了轉頻的范圍,進行了帶通濾波處理,提高了轉頻信息提取的可靠性;最后,進行了實驗,從裝置的振動信號中提取出了轉子的轉頻信息,并計算了其轉速。

主要結論如下:

1)旋轉式能量回收裝置的振動中含有與轉子轉頻相關的特征,其中因內孔道水錘沖擊作用造成的8倍轉頻振動最為顯著。其次為外孔道水錘沖擊造成的16倍轉頻,此外,1倍轉頻及其諧波在高轉速時也較為明顯。因此,在多數情況下,8倍轉頻都是裝置振動的主要頻率,可以通過識別振動信號中的8倍轉頻,計算得到轉子的轉頻;

2)采用小波變換可以有效消除旋轉式能量回收裝置振動信號的基線漂移;使用Hilbert包絡可以凸顯轉頻的倍頻信號特征;通過振動能量估計轉頻范圍并進行帶通濾波處理,可以保留8倍轉頻并避免其余倍頻的干擾,提高轉速計算的準確率;

3)根據實驗結果,在裝置平穩運轉狀態下,通過振動信號計算得到的轉速與直接測量的轉速,其最大誤差率為2.55%,在非平穩運轉狀態下的最大誤差率為4.58%。該方法可以使裝置在線運行的條件下,通過采集振動信號,實時測量能量回收裝置的轉子轉速。

在未來的研究工作中,筆者將進一步改進信號的處理算法,提高轉速測量方法的穩定性和準確性,并研究該方法在檢測裝置運轉狀態方面的應用。