基于自適應反步滑模與死區逆補償的閉式泵控系統位置輸出控制策略*

王 飛,劉會龍,劉 焱,陳革新,劉克毅*,艾 超

(1.新疆工程學院 機電工程學院,新疆 烏魯木齊 830023;2.燕山大學 機械工程學院,河北 秦皇島 066004)

0 引 言

電液伺服泵控系統是一種高集成的閉式容積伺服驅動單元,由伺服電機、定量泵、功能閥組和執行元件等組成。該泵控系統具有高效環保、高功重比、承載能力強以及成本低等優點[1],目前已被廣泛應用在國防、工業領域中,如飛機的舵機系統[2]、船艦與潛艇的舵機系統[3]、工程機械[4]等控制系統。

在電液伺服閉式泵控系統的位置輸出控制過程中,系統的內部存在著油液彈性模量、流量泄漏系數、負載等效彈簧剛度與液壓缸黏性摩擦系數等參量攝動,系統外部負載存在擾動,呈現出較強的時變性和非線性特性[5]。同時,在泵控系統的運行起始與低速控制階段,由于系統內部的油液存在壓縮與泄漏,使得系統的輸出滯后,會出現系統死區,導致控制精度降低、系統不穩定與動態品質下降等問題的出現[6]。

在電液泵控位置伺服系統中,針對參數時變性及非線性等因素的影響,目前,專家學者們采用了反饋線性化、自適應控制、滑模控制及模糊控制等技術進行了研究。其中,自適應控制結合反步法,能很好地處理系統中的不確定性和未知參數。對于系統參數攝動與干擾方面,滑模控制具備較強的魯棒性。而針對系統死區補償的研究,目前都采用的方法是,將死區等效為系統所受到的擾動,利用魯棒控制器對系統死區進行抑制。

付永領等人[7]提出了一種新型的恒轉矩、變排量電液伺服泵控單元和一種自適應反步控制算法,采用該單元和算法提高了系統位置跟蹤性能,極大地降低了電機的最大額定轉矩。陳革新等人[8]提出了一種以反步設計為基礎的非線性自適應控制策略,對擾動實時在線調節不確定參數,對自適應率進行了設計,提高了系統的精確度,增強了系統的魯棒性。郭新平等人[9]以泵控電液伺服系統為研究對象,以滑模控制理論為基礎,結合滑模控制器和擴展式觀測器,設計了滑模結構控制算法,利用MATLAB/Simulink和AMESim仿真平臺進行了聯合仿真驗證,結果表明,所設計的觀測器可以精確估計干擾,且對外部干擾具有較強的魯棒性,提高了泵控電液伺服系統位置輸出控制的控制性能。郭楠等人[10]針對泵控液壓錨桿鉆臂旋轉系統出現的內外部干擾問題,基于動態切換函數,設計了一種的滑模自適應擺角控制器,采用該控制器有效降低了系統的抖振,抑制了干擾,仿真實驗表明,所設計的控制器能有效克服諸多不確定性因素,準確跟蹤系統設定值。WANG H D等人[11]研究了水下航行器機械手系統(underwater vehicle manipulator system,UVMS)的自適應模糊控制問題,提出了一種新型的預死區補償器,以此來抑制死區的影響,并通過仿真驗證了該控制方案在解決UVMS存在死區帶和擾動下跟蹤控制問題方面的有效性。王立新等人[12]考慮了電液比例位置同步液壓系統受元件安裝精度、參數攝動以及系統死區非線性等因素的影響,提出了一種由位置控制器、同步控制器和死區補償器組成的復合控制方案,研究結果表明,死區補償器的加入有效改善了系統的動態響應性能,降低了系統的穩態位置同步誤差。

綜上所述,針對電液伺服閉式泵控系統位置輸出控制過程中系統的參數不確定性及系統死區問題等,學者們從自適反步控制、滑模控制和死區補償單個方面或者兩者結合的角度分別進行了相關的研究;但目前尚未見同時將三者相結合的研究文獻。

為此,在考慮電液伺服閉式泵控系統位置輸出控制過程中參數不確定性和系統死區等因素基礎上,筆者提出一種自適應反步滑模控制與死區逆補償控制組合的控制策略;同時,利用系統參數自適應律對不確定性參數擾動進行實時在線調節,并采用光滑死區逆函數對系統死區進行補償;最后,為了驗證該串聯控制方法的有效性,構建系統MATLAB/Simulink仿真模型,并進行分析。

1 電液伺服閉式泵控系統原理

筆者研究的對象電液伺服閉式泵控系統(簡稱泵控系統)主要由電氣部分與液壓部分兩部分組成。其中,液壓部分由伺服電機、定排量泵、補油模塊、安全模塊與作動器單元等組成。

電液伺服閉式泵控系統工作原理圖如圖1所示。

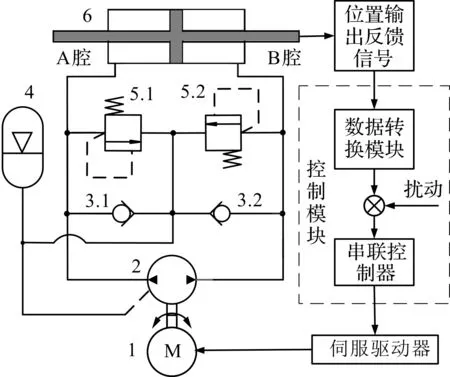
圖1 電液伺服閉式泵控系統工作原理圖

圖1中:系統工作時,采用伺服電機1同軸驅動定排量泵2,定排量泵吸排油口與液壓缸6兩負載油口直接連接,蓄能器4配合單向閥3.1、3.2對系統進行補油,2個溢流閥5.1、5.2作為安全閥保護系統壓力不超出安全限定值。

電氣部分由位置輸出反饋裝置、控制模塊與伺服驅動器組成,位置輸出反饋裝置采集液壓缸活塞桿位移信號,控制模塊對信號進行處理,由串聯控制器輸出轉速控制指令到伺服驅動器,進而控制伺服電機的輸入電壓,實現實時調節輸出轉速目的,最終控制定排量泵輸出壓力與流量,達到對液壓缸活塞輸出位置控制的目的。

2 電液伺服閉式泵控系統數學模型

基于上述電液伺服閉式泵控系統原理,筆者建立系統各關鍵液壓元件的數學模型。

2.1 伺服電機模型

泵控系統在進行位置控制過程中,伺服電機將控制輸入電壓轉化成電機的輸出轉速。筆者考慮伺服電機具有較高的響應速度和控制精度,可以將電機輸出轉速與輸入控制信號之間的關系簡化為比例環節,其表示如下:

ωp=Kmuc

(1)

式中:ωp為定量泵輸入轉速,r/min;Km為控制增益,r/(s·V);uc為控制輸入信號,V。

2.2 定量泵模型

考慮到油液壓縮與內外泄漏等因素,從泵到被控液壓缸的兩腔負載容積流量可表示為:

(2)

式中:QA,QB為定量泵輸出和吸入流量,m3/s;DP為定量泵排量,L/r;pA,pB為泵的出口和進口壓力,Pa;Cip,Cep為泵的內外泄漏系數,(m3·s)/Pa。

2.3 雙作用對稱液壓缸模型

在考慮負載工況、腔室油液壓縮與液壓缸內外泄漏等因素后,筆者建立了雙作用對稱液壓缸兩腔流量連續性方程:

(3)

式中:qA,qB為流入液壓缸A腔和流出B腔油液的流量,m3/s;Ac為雙作用對稱液壓缸有效工作面積,m2;xc為活塞位移,m;βe為包含油液、液壓缸缸體和連接管道的機械柔度在內的有效體積彈性模量,Pa;VcA,VcB為液壓缸A、B腔壓縮容積,m3;Cic,Cec為液壓缸內外泄漏系數,(m3·s)/Pa。

式(3)可簡化為[13]:

(4)

式中:Vt為總壓縮容積,m3。

雙作用對稱液壓缸活塞桿受力平衡方程為:

(5)

式中:mc為液壓缸活塞等效總質量,kg;Bc為系統油液黏滯阻尼系數,N/(m·s);K為系統負載等效彈簧剛度,N/m;F為液壓缸活塞上負載力,N。

聯立式(1)～式(5),可得:

(6)

式中:Ct=Ctc+Ctp=Cic+Cec/2+Cip+Cep/2為系統總泄露系數,(m3·s)/Pa。

結合泵控系統的數學模型,筆者構建出了電液伺服閉式泵控系統的MATLAB/Simulink仿真模型,并根據研究條件配置了系統主要參數。

電液伺服閉式泵控系統仿真模型如圖2所示。

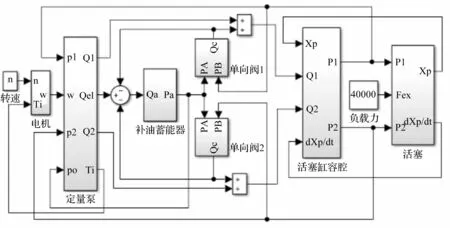
圖2 電液伺服閉式泵控系統仿真模型

電液伺服閉式泵控系統主要參數如表1所示。

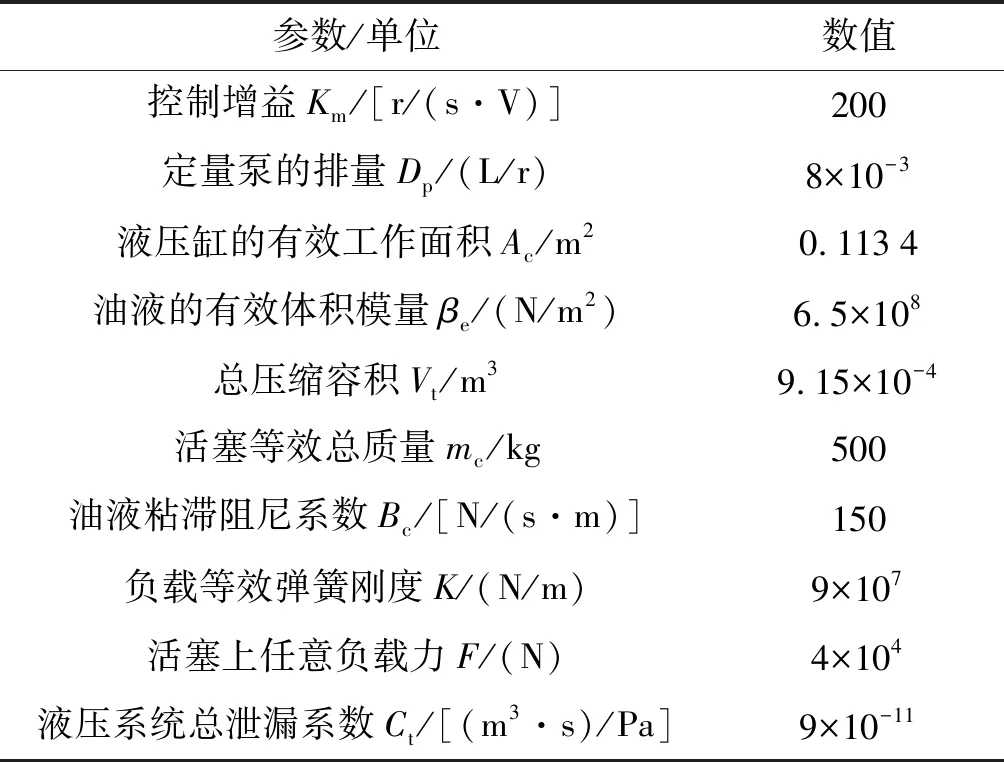
表1 電液伺服閉式泵控系統主要參數

3 控制器設計

根據自適應反步控制原理設計出的自適應控制器易出現控制律與參數自適應律之間相互嵌套的問題,影響系統的控制性能。此外,泵控系統死區也會影響系統閉環響應特性,導致系統出現跟蹤性能差、響應遲滯等一系列問題。

為此,筆者在自適應反步控制器設計的過程中引入滑模控制原理,設計出了自適應反步滑模控制器,以此來消除系統非匹配與匹配不確定項帶來的影響,又避免了控制律與參數的自適應律之間相互嵌套問題的發生;同時,采用平滑連續指標函數,設計了光滑死區逆函數和死區逆補償控器,以解決因死區逆函數不光滑而引起的抖振問題。

3.1 自適應反步滑模控制器設計

自適應反步控制方法可以消除系統非匹配不確定項帶來的影響,但在參數自適應率修正時,會產生“計算膨脹”問題。而滑模控制方法在系統不確定項滿足匹配條件的情況下具有較強的魯棒特性。因此,將兩者結合的自適應反步滑模控制可以很好地處理系統的不確定性問題。

自適應反步滑模控制同樣基于反步遞推準則設計,其設計過程可以分為4步,具體如下[14]:

1)步驟一

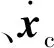
(7)

由式(1)～式(6)可知,電液伺服閉式泵控系統非線性模型狀態空間的嚴格反饋形式可表示為:

(8)

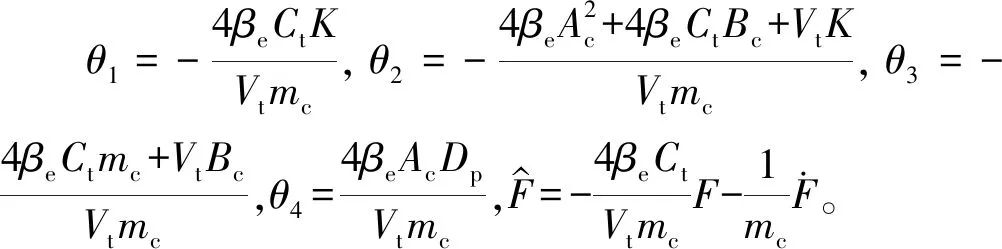
2)步驟二

電液伺服泵控系統的控制目標為實際輸出位置能夠較好地追蹤輸出期望值。

定義其位置誤差為:

e1?x1-x1d

(9)

式中:x1d為狀態變量x1的期望值。

定義二級子系統狀態誤差為:

e2=x2-x2d

(10)

式中:x2d為狀態變量x2的期望值。

定義x2d為:

(11)

式中:k1為大于0的正常數。

定義第1個Lyapunov函數:

(12)

由式(9)～式(12)可得:

(13)

3)步驟三

再定義第2個Lyapunov函數:

(14)

定義e3為狀態變量x3與其對應的虛擬控制變量x3d之間的偏差:

e3=x3-x3d

(15)

定義x3d為:

(16)

式中:k2為大于0的正常數。

由式(14)～式(16)可得:

(17)

4)步驟四

為了避免發生參數相互嵌套問題,筆者在此引入滑模控制方法。定義滑模切換函數為:

s=c1e1+c2e2+e3

(18)

式中:c1>0、c2>0為滑模面常數。

為避免出現控制律與參數自適應律循環嵌套問題,筆者所設計的參數自適應率中不得含有控制輸入量uc。基于此,構建Lyapunov函數為:

V3=V2+s2/(2θ4)≥0

(19)

對上式求導可得:

(20)

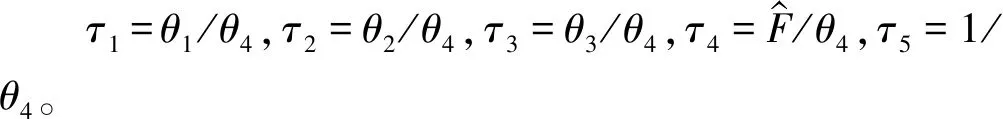
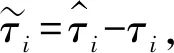
取系統Lyapunov函數為:

(21)

式中:γi為相應參數τ1、τ2、τ3、τ4與τ5的參數自適應增益,γi>0(i=1,…,5)

對上式求導,取k3>0,筆者所設計的自適應滑模控制器電壓控制率為:

(22)

取參數的自適應率為:

(23)

此時有:

(2k3c2-1)e2e3-2k3c1e1e3=-ETQE

(24)

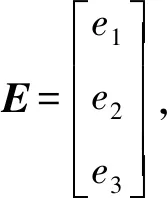
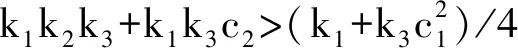
3.2 死區逆補償器設計

由液壓泵流量死區、功能閥泄露及液壓缸輸出死區等綜合作用所導致的死區,稱為“系統死區”。系統死區的存在容易導致控制精度降低、動態品質下降與系統不穩定等問題的出現。

在工程實踐中,對“系統死區”進行補償具有重要的實用價值。大多數的非線性系統死區函數都是不光滑的,由此構造的非線性系統死區逆函數雖然具有死區逆補償控制功能,但是會產生一定的抖振現象。

為了實現死區補償控制的目的,筆者利用平滑連續指標函數構造光滑死區逆函數,設計了死區逆補償控制器[15]。

3.2.1 死區逆補償原理

此處給出的系統模型如下:

(25)

式中:ai和b都為系統的未知常數;x(t)為系統的狀態變量;Yi(x(t))為系統狀態參量的函數;y為系統的輸出;u為控制系統的輸入;D(v(t))為液壓缸系統死區特性;v(t)為設計控制器的輸出。

系統死區逆補償即是設計一個輸出反饋控制律,以確保系統全部閉環信號都是有界的。記yr(t)為系統輸出y(t)的給定跟蹤信號,假設未知常數b的符號已知,yr(t)及其前n階導數已知且是有界的。

則死區特性D(v)表示為:

(26)

式中:br,bs,mr和ms為系統死區參數,滿足mr>mr0和ms>ms0,其中,mr0和ms0是2個小的正常數,br≥0、bs≤0、mr>0、ms>0,且都是常數。通常情況下,斷點和斜率不對稱,即|br|≠|bs|,mr≠ms。

補償死區效應的本質是采用死區逆,故筆者利用平滑連續指標函數構造光滑死區逆函數,如下所示:

(27)

式中:x1d為狀態變量x1的期望值。

其中,ψr(u)=eu/e0/(eu/e0+e-u/e0)和ψs(u)=e-u/e0/(eu/e0+e-u/e0)為平滑連續指標函數,e0>0,且ψr(u)=1-ψs(u)。

3.2.2 死區逆補償器估計參數設計

此處,筆者選擇以鋰電池極片軋機電液伺服泵控AGC系統為本次測量系統死區的實驗平臺。該系統應用于設備軋輥定輥縫和定軋制力高性能控制[16,17]。

鋰電池極片軋機電液伺服泵控AGC工作原理如圖3所示。

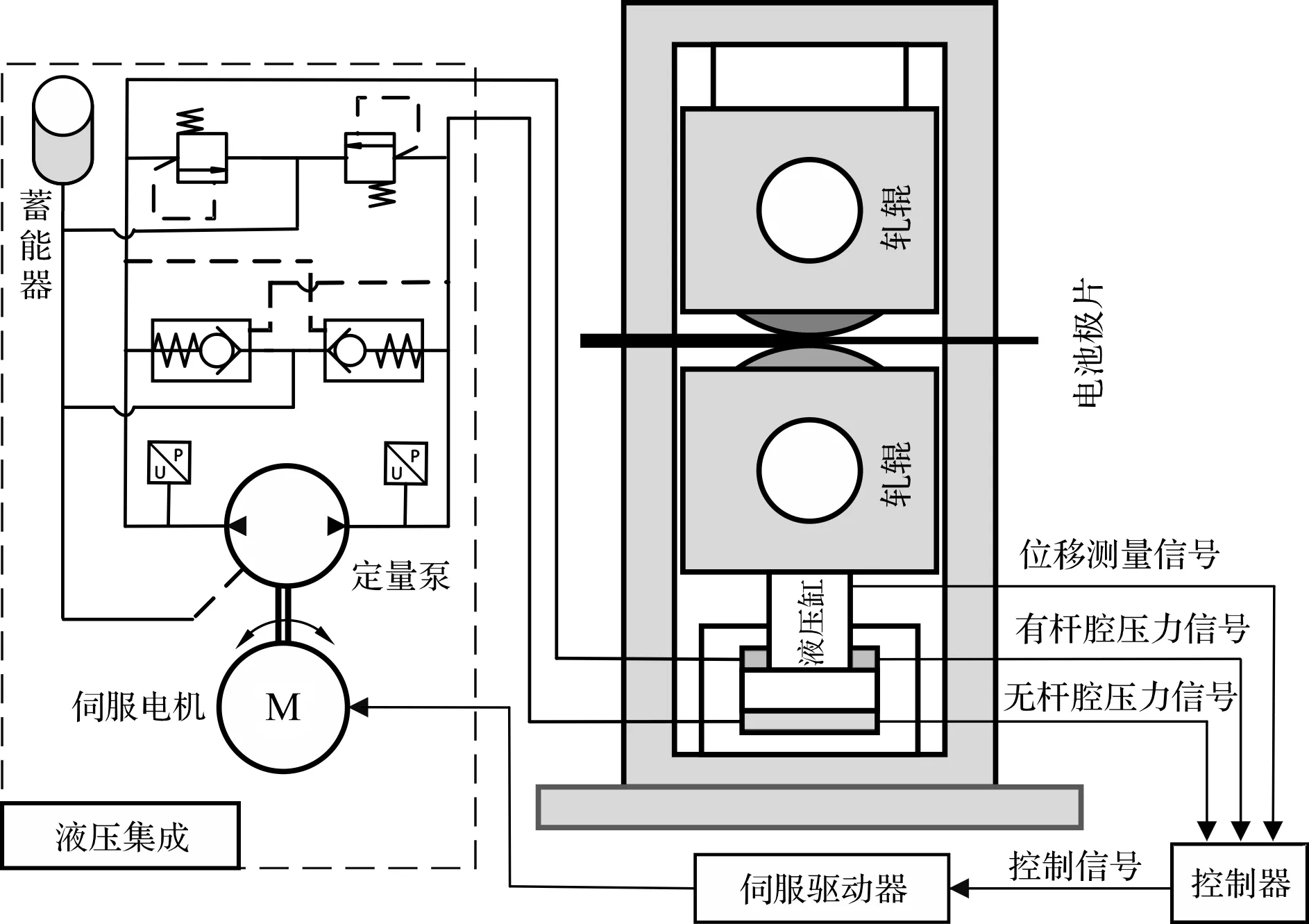
圖3 鋰電池極片軋機電液伺服泵控AGC工作原理圖

筆者在上述平臺上進行系統死區測量[18,19]:

1)將液壓缸活塞置于完全縮回位置點,向伺服電機輸入0.5 V/s的遞增電壓信號,記錄活塞伸出位移xc與電機轉速n數據,繪制系統正向死區曲線;

2)將液壓缸活塞置于完全伸出位置點,向伺服電機輸出0.5 V/s的遞減電壓信號,記錄活塞伸出位移xc與電機轉速n數據,繪制系統負向死區曲線;

3)分別做出系統正、負向死區的參考線,獲得死區估計參數。

系統死區曲線如圖4所示。

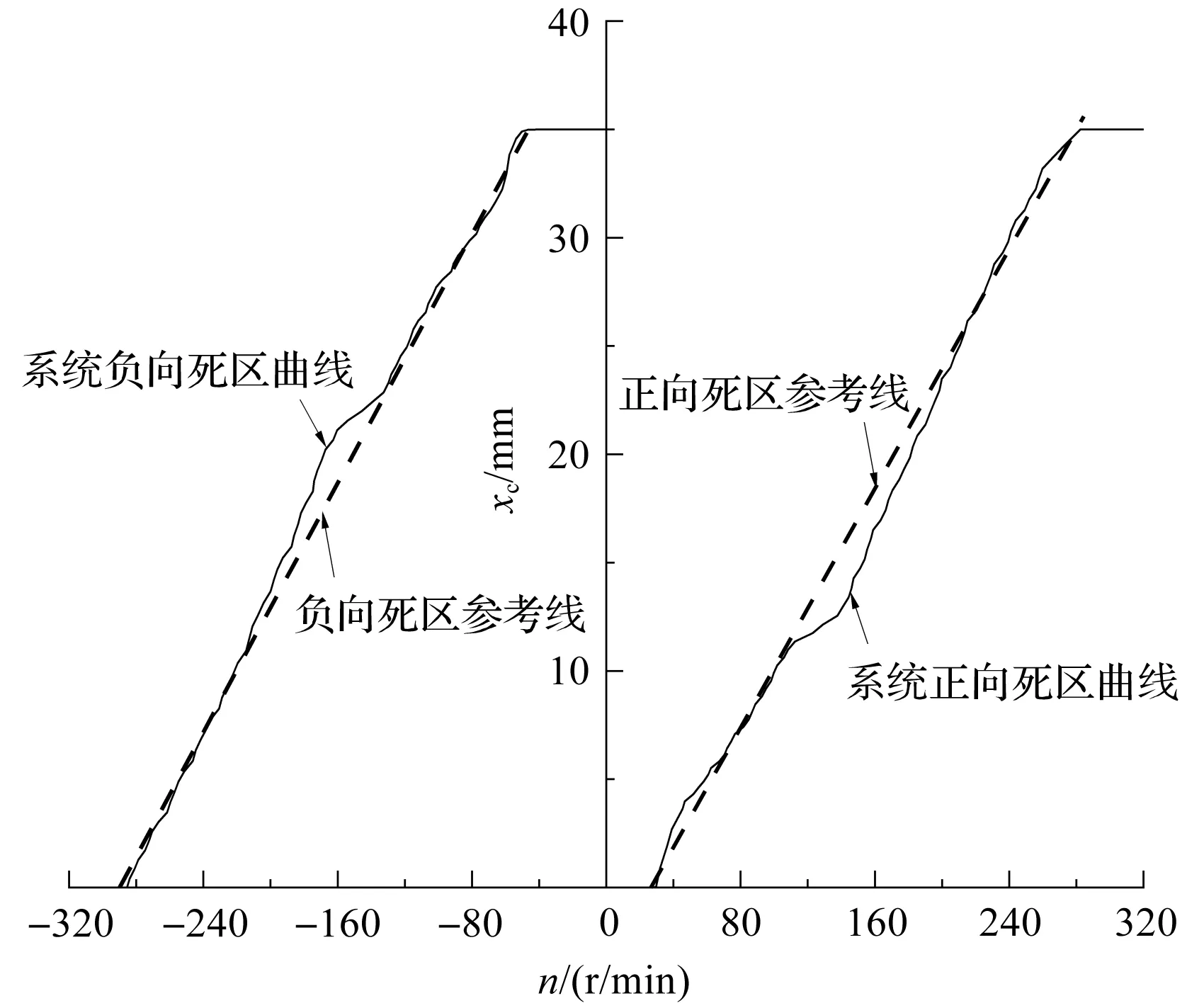
圖4 系統死區曲線

由圖4可以得到:參數br=27.92,bs=47.31,mr=0.136,ms=0.142,將其代入式(27)中,即可得到系統死區逆補償控制器。

最后,筆者將自適應反步滑模控制器與系統死區逆補償控制器相結合,組成閉式泵控系統位置控制串聯控制器,用于電液伺服閉式泵控系統位置輸出控制。

泵控系統串聯控制構架框如圖5所示。

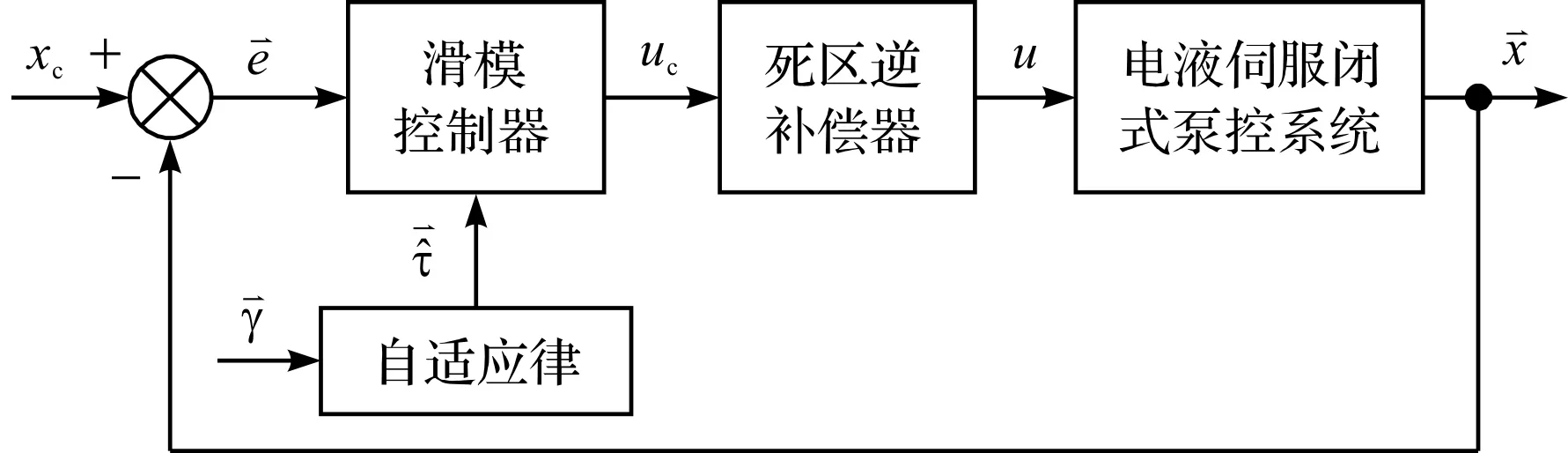
圖5 泵控系統串聯控制構架框圖

4 仿真結果與分析

筆者將在MATLAB/Simulink環境中完成自適應反步滑模控制器與死區逆補償器構建組合成的串聯控制器,將其與電液伺服泵控系統MATLAB/Simulink仿真模型相結合,組成閉式泵控系統位置輸出串聯控制器MATLAB/Simulink仿真模型。

自適應反步滑模控制器參數取為:c1=2.5×10-2,c2=4×10-2,k1=250,k2=1.7×108,k3=2×104,γ1=4 000,γ2=3.5×105,γ3=2×106,γ4=1×1015,γ5=1×1022。

閉式泵控系統位置輸出串聯控制器仿真模型如圖6所示。

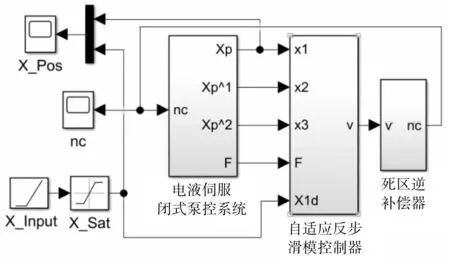
圖6 閉式泵控系統位置輸出串聯控制器仿真模型

筆者對系統施加初始值為0 μm的50 μm斜坡信號,并在串聯控制器作用下,觀察記錄液壓缸活塞位移xc和位置誤差e,得到串聯控制器輸出位移曲線和位移誤差曲線。

串聯控制器位移曲線如圖7所示。

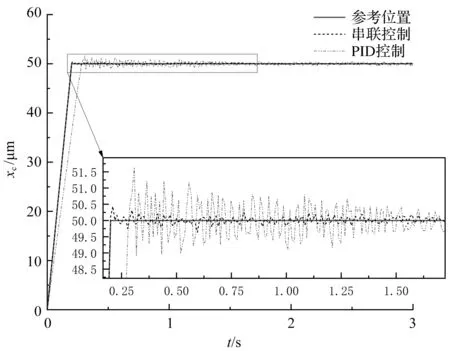
圖7 串聯控制器位移曲線

由圖7可知:由自適應反步滑模控制器與死區逆補償控制器所組成的串聯控制器,其位移曲線表現出了很好的跟隨性。

串聯控制器位移誤差曲線如圖8所示。

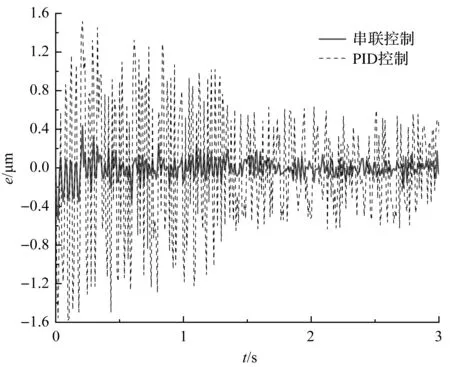
圖8 串聯控制器位移誤差曲線

由圖8可知:采用了串聯控制器的位移跟隨精度可以達到±0.6 μm,穩態精度則達到±0.3 μm,系統到達穩態的時間大約為0.6 s;采用PID控制時,位移跟隨精度為±1.6 μm,穩態精度則達到±0.6 μm,系統到達穩態的時間大約為1.3 s。

同時,仿真結果與文獻[8]中單獨應用自適應反步滑模控制器的試驗結果相比,位移跟隨精度和位置穩態精度都有所提高,這證明所設計的串聯控制器對閉式泵控系統位置輸出控制有良好的效果;但是串聯控制器結構更為復雜。

自適應反步滑模控制器參數的變化曲線與死區逆補償器輸出控制轉速曲線,如圖9所示。

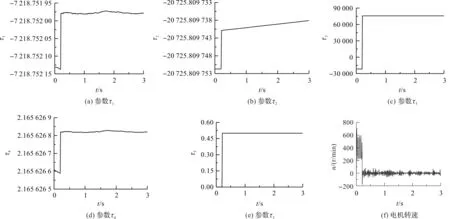
圖9 串聯控制器參數曲線

由圖9可知:系統采用自適應反步滑模控制器與死區逆補償器組成的串聯控制器進行位置控制時,在自適應反步滑模控制器參數自適應律的作用下,系統不確定性參數τ1、τ2、τ3、τ4與τ5進行實時調整,進而調節控制輸出信號至死區逆補償器,在死區逆補償器作用下輸出控制轉速n,使控制系統趨于穩定,轉速也趨于穩定,提高了系統穩態控制精度。

5 結束語

筆者提出了一種將自適應反步滑模控制器與死區逆補償控制器相結合的控制策略;設計了串聯控制器,用于解決電液伺服閉式泵控系統位置輸出控制過程中的參數不確定性及系統死區問題;最后搭建了MATLAB/Simulink仿真模型,并進行了結果分析。

研究結論如下:

1)筆者提出的自適應反步滑模控制器與死區逆補償控制器結合構成的串聯控制器,其具有良好的控制性能。采用了串聯控制器的系統位移跟隨精度可以達到±0.6 μm,穩態精度則可以達到±0.3 μm,系統在0.6 s左右時到達穩態;

2)在系統位置的控制過程中,其不確定性參數在參數自適應律的作用下能夠進行實時調整,最終輸出穩定的轉速,提高了系統穩態控制精度。

筆者設計的串聯控制器結構較復雜,在具體工程應用推廣環節還需要做進一步的優化,以提高系統的控制精度。