充分條件、必要條件、充要條件題型解析

■朱 珠

充分條件與必要條件是高中數(shù)學的重要概念,因其抽象性而成為同學們難以理解的內(nèi)容。下面就這方面的題型進行舉例分析。

一、充分條件、必要條件、充要條件的判斷

充分條件與必要條件:若p?q,則p是q的充分條件,q是p的必要條件;若p?/q,則p不是q的充分條件,q不是p的必要條件。一般地,如果p?q,且q?p,就記作p?q,則p是q的充分必要條件,簡稱充要條件。概括地說,如果p?q,那么p與q互為充要條件。判斷p是q的什么條件,主要判斷p?q,及q?p這兩個命題的正確性,若p?q真,則p是q成立的充分條件;若q?p真,則p是q成立的必要條件。要否定p與q不能相互推出時,舉出一個反例即可。

例1(1)已知實系數(shù)一元二次方程ax2+bx+c=0(a≠0),則下列結論正確的是( )。

①Δ=b2-4ac≥0是這個方程有實根的充要條件;②Δ=b2-4ac=0 是這個方程有實根的充分條件;③Δ=b2-4ac＞0 是這個方程有實根的必要條件;④Δ=b2-4ac＜0是這個方程沒有實根的充要條件。

A.③④ B.②③

C.①②③ D.①②④

(2)若p:A∩B=A,q:?UB??UA,則p是q的( )。

A.充分不必要條件

B.必要不充分條件

C.充要條件

D.既不充分也不必要條件

分析：對于(1),利用Δ=b2-4ac判斷方程根的情況,當Δ=0時,一元二次方程有兩個等根;當Δ＞0時,一元二次方程有兩個不相等的根;當Δ＜0時,一元二次方程沒有實數(shù)根。對于(2),畫出Venn圖(如圖1),結合圖形,可幫助求解。

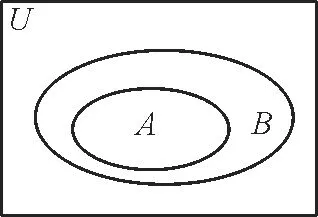
圖1

解：(1)Δ≥0?一元二次方程ax2+bx+c=0(a≠0)有實根,①正確。Δ=0?一元二次方程ax2+bx+c=0(a≠0)有實根,②正確。Δ＞0?一元二次方程ax2+bx+c=0(a≠0)有實根,但ax2+bx+c=0(a≠0)有實根?/Δ＞0,③錯誤。Δ＜0?一元二次方程ax2+bx+c=0(a≠0)無實根,④正確。應選D。

(2)結合圖1可得A∩B=A?A?B??UA??UB,即p是q的充要條件。應選C。

充分條件與必要條件的兩種判斷方法:直接利用定義判斷;集合法,將命題p,q分別看作集合A,B,當A?B時,p是q的充分條件,q是p的必要條件,當A=B時,p,q互為充要條件。

二、充分條件、必要條件、充要條件的應用

利用充分條件、必要條件求參數(shù)的取值范圍問題,常利用集合法求解,先化簡集合A={x|p(x)}和B={x|q(x)},然后根據(jù)p與q的關系(充分、必要、充要條件),得出集合A與B的包含關系,進而得到相關不等式組,最后求出參數(shù)的取值范圍。

例2已知集合A={x|a＜x＜a+2},B={x|x＜-1或x＞3},且A是B的充分不必要條件,求實數(shù)a的取值范圍。

分析：由A是B的充分不必要條件,說明集合A是B的真子集,即AB,由此可得實數(shù)a滿足的條件,從而得到實數(shù)a的取值范圍。

解：因為A是B的充分不必要條件,所以AB。又因為A={x|a＜x＜a+2},B={x|x＜-1 或x＞3},所以a+2≤-1或a≥3,解得a≥3或a≤-3,所以實數(shù)a的取值范圍是{a|a≥3或a≤-3}。

充分條件、必要條件中的含參數(shù)問題,往往是通過集合的包含關系來解答的。

三、充要條件的證明

充要條件的證明,可分為充分性和必要性的證明,證明時要注意兩種敘述方式的區(qū)別:①p是q的充要條件,由p?q是充分性,由q?p是必要性;②p的充要條件是q,由p?q是必要性,由q?p是充分性。

例3求證:方程mx2-2x+3=0有兩個同號且不相等實根的充要條件是

分析：先找出條件和結論,然后證明充分性和必要性都成立。

綜上可得,方程mx2-2x+3=0有兩個同號且不相等的實根的充要條件是

證明p是q的充要條件,既要證明命題“p?q”為真,又要證明“q?p”為真,前者證明的是充分性,后者證明的是必要性。證明充要條件,即證明原命題和逆命題都成立。要注意“p是q的充要條件”與“p的充要條件是q”這兩種說法的差異,要分清哪個是條件,哪個是結論。

1.求證:關于x的方程ax2+bx+c=0有一個根是1的充要條件是a+b+c=0。

提示:先證明p?q,即證明必要性,再證明q?p,即證明充分性。設命題p:方程ax2+bx+c=0有一個根是1,命題q:a+b+c=0。先證明p?q,即證明必要性,由x=1是方程ax2+bx+c=0的根,可得a·12+b·1+c=0,即a+b+c=0。再證明q?p,即證明充分性,由a+b+c=0,可得c=-a-b,因為ax2+bx+c=0,所以ax2+bx-a-b=0,即a(x2-1)+b(x-1)=0,也即(x-1)(ax+a+b)=0,所以x=1是方程的一個根。綜上可知,方程ax2+bx+c=0有一個根是1的充要條件是a+b+c=0。

2.已知三個不等式:ab＞0,bc-ad＞0,(其中a,b,c,d均為實數(shù))。用其中兩個不等式作為條件,余下的一個不等式作為結論組成一個命題,則可組成的正確命題的個數(shù)是( )。

A.0 B.1 C.2 D.3