強噪聲下基于混沌技術的高超聲速飛行器傳感器故障診斷

2023-09-22 12:55:06黃鵬飛屈劍鋒陳小龍

宇航學報 2023年8期

黃鵬飛，屈劍鋒，柴毅，陳小龍，劉切

(重慶大學自動化學院，重慶 400044)

0 引言

高超聲速飛行器指飛行速度大于馬赫數5的飛行器,其超高速度飛行、強機動等特性使其具有極高的軍事價值和經濟價值。近年來,高超聲速飛行器的設計、控制和故障診斷等受到極大關注[1-3]。

為準確監測和控制高超聲速飛行器,其上安裝了數量龐大的傳感器。然而,由于高超聲速飛行帶來的薄激波層[4]、熵層和高溫氣體等效應,以及飛行環境的多變、強干擾、強震蕩、過載等因素,使得飛行器傳感器極易發生故障。飛行器傳感器故障不僅會帶來測量偏差,導致監控精度的下降,還會由于系統的耦合、信息的傳播等誘發安全事故。因此,研究高超聲速飛行器傳感器的故障診斷,對保障高超聲速飛行器的精準控制和安全飛行具有重要意義。超高聲速飛行器飛行過程是典型的非線性、強耦合過程,且由于飛行環境復雜,飛行測量參數受到較大噪聲的污染,這為傳感器故障診斷帶來極大挑戰。

為實現高斯和非高斯噪聲下的故障檢測,Safaeipour等[5]提出了一種自適應魯棒殘差估計方法,然而,該方法只考慮了有限功率的噪聲。He等[6]研究并比較了幾種不同飛行器傳感器故障檢測和診斷方法,但未對非高斯噪聲進行討論,并且所考慮的噪聲功率較小。滑模方法被廣泛地應用于故障檢測和診斷領域[7],但這種方案因不直接處理噪聲,使得其在強噪聲情況下性能有限。Mei等[8]采用模糊自適應滑模方法,解決了參數不確定性和空間干擾等因素下的故障估計問題,但該方法沒有深入分析強噪聲情況下的性能。李娟等[9]研究了大時滯和噪聲下的故障診斷問題,但僅考慮了功率有限的白噪聲,缺乏對非理想噪聲的研究。羅小元等[10]針對噪聲統計特性未知情況下的虛假數據檢測和估計,提出了一種自適應卡爾曼濾波器,但是噪聲功率較大情況未見分析。在工程設計中,通常假設系統中的噪聲為高斯噪聲,然而在實際中,非高斯噪聲[11]也是廣泛存在的,因此,為保證所設計故障診斷算法的魯棒性[12-13],有必要考慮非高斯噪聲、強噪聲情況下的故障診斷。針對上述問題,本文考慮設計一種可同時處理強高斯噪聲和非高斯噪聲且無需獲取或假設噪聲統計特性等信息的方法,以實現強噪聲下的傳感器故障診斷。

混沌系統是一種典型的非線性系統,其確定但不可預測的特殊動力學行為吸引了諸多國內外學者。隨著對混沌研究的不斷深入,混沌系統在實際工程中的應用也不斷被發掘。混沌系統具有初值敏感性和噪聲免疫特性,因此其被廣泛應用于微弱信號檢測中,如Duffing混沌系統[14]。當待測信號作為外部驅動引入系統時,可引起系統相變,通過對系統參數的調節,可在低信噪比下實現信號幅值、周期等信息的檢測。與Duffing混沌系統不同,美國氣象學家L. O. Lorenz提出的Lorenz系統是一種自治系統[15],它不需要外部信號的激勵便可以產生混沌震蕩,因而在信號檢測領域少見應用。分數階混沌系統憑借其更加豐富的動力學行為也逐漸得到越來越多的關注[16]。分數階混沌系統在故障診斷中的使用剛剛起步,本文針對強高斯和非高斯下噪聲故障特征不明顯、故障診斷困難的問題,研究基于分數階混沌系統的信號處理方法和基于機器學習的傳感器故障診斷方法。

本文的主要創新點包括:

1)設計并采用了分數階混沌系統進行信號處理和故障特征提取,可有效降低強高斯噪聲和非高斯噪聲的影響,且無需獲取或假設噪聲的概率分布。

2)提出了一種利用模型仿真生成故障數據集并結合機器學習模型實現故障診斷的方法。可作為高超聲速飛行器故障診斷的預訓練模型。

本文的組織結構如下:第1節對研究的問題進行了描述,包括高超聲速飛行器的模型、所研究的迎角傳感器故障類型以及噪聲模型等。第2節對提出的故障診斷方法進行了闡述,分析了分數階混沌系統的參數對其動力學行為的影響,并介紹了所構建的故障數據集。第3節開展了實驗驗證,第4節對全文工作進行了總結。

1 問題描述

1.1 高超聲速飛行器模型

高超聲速飛行器飛行過程是典型的非線性過程,其動力學模型為[1]:

(1)

式中:V表示高超聲速飛行器在平面地球條件下的速度;Z是其質心坐標;θ和α分別為其航跡角和迎角;ωy是其俯仰角速度;D和C分別表示其所受的阻力和側向力;Tx為其發動機推力;Myy是其俯仰力矩;Iyy為轉動慣量;m為其質量。

在一定的飛行狀態下,給定飛行速度和高度后,在縱向方向上,將高超聲速飛行器模型進行線性化,并將其視作剛體,則高超聲速飛行器縱向線性模型為:

(2)

式中:X(t)=[v,α,η,h,θ]T為縱向模型系統狀態,即高超聲速飛行器飛行速度、飛行迎角、迎角角速度、飛行高度和俯仰角;U(t)為系統輸入;Y(t)為輸出信號;A為系統矩陣;B為輸入矩陣;C為輸出矩陣;D為直接傳遞矩陣。飛行器工作條件惡劣,高溫、強震動、高過載等使得飛行器易受擾動、噪聲和傳感器故障等影響,這對高超聲速飛行器服役的安全性和可靠性帶來嚴峻挑戰。迎角傳感器(AOA)是極易出現故障的設備[1,17],且故障類別具有典型性,因此,本文以迎角傳感器為例研究高超聲速飛行器傳感器故障診斷問題。

考慮飛行器飛行存在未知擾動和測量噪聲的情況,將系統模型(2)進一步寫為[18]

(3)

式中:ν(t)為隨機擾動;υ(t)表示測量噪聲;f(t)表示傳感器故障的大小;Ff為相應的參數矩陣。同時,采用狀態反饋使系統穩定。鑒于高超音速的大迎角飛行特性,將高超聲速飛行器迎角的控制目標設置為45°。

1.2 迎角傳感器故障類型

1.2.1數據偏離故障

超高聲速飛行器在飛行過程中存在再入大氣層、拉起、大氣層內滑翔等多個階段,不同階段下飛行器所處環境不同、飛行速度不同,引起機身溫度劇烈變化,進而導致迎角傳感器可能出現數據偏離故障。數據偏離故障的大小可表示為

fb=bfu(t-τb)

(4)

式中:bf為偏離量;τb表示數據偏離故障的出現時間;u(t)為單位階躍函數。

1.2.2卡滯故障

當超高聲速飛行器飛行速度較低時,入射流溫度低于0 ℃,使得傳感器易發生卡滯故障。設卡滯故障出現時,迎角傳感器輸出為0。

1.2.3增益變化故障

超高聲速飛行器飛行速度快,在飛行過程中和空氣存在劇烈的摩擦,期間會產生大量的熱,一方面會引起傳感器輸出噪聲增大,另一方面則會引起增益變化故障,假設增益不變且呈線性增大的趨勢,則該故障的大小為

fd=df(t-τd)

(5)

式中:df表示增益變化斜率;τd是故障出現時間。

1.2.4異常值故障

由于超高聲速飛行器飛行速度快,其風向標的縱橫比影響機身周圍的局部氣流,并引起局部激波,可能會導致傳感器出現異常值故障,該故障大小為

(6)

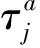
1.3 非高斯測量噪聲模型

超高聲速飛行器在飛行的過程中,復雜、多變且惡劣的環境為其帶來嚴重的擾動和測量噪聲。一般地,測量噪聲常考慮高斯噪聲,然而,在實際情況下,考慮到復雜的電磁對抗、干擾等,本文考慮了監測信號存在拖尾噪聲的情況,其模型為

(7)

式中:p1,p2,p3和p4是外部配置概率參數;σ2為方差;1,2,3和4為相應的區間。

拖尾噪聲下,迎角傳感器的故障信號如圖1所示。由于強噪聲的存在,故障數據和正常數據之間的相似度較大,且故障信號之間的相似度也較大,這為故障診斷帶來了極大挑戰。

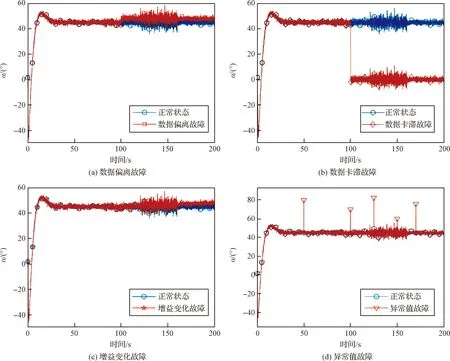
圖1 拖尾噪聲和不同故障模式下迎角傳感器輸出信號Fig.1 The signals of AOA sensor under heavy-tailed noise and different faults

2 基于分數階混沌系統的傳感器故障診斷方法

基于模型的故障診斷方法通常需要根據預測值和實測值之間的殘差來分析系統運行狀態,但是這種方法依賴精確的數學模型,并且隨著系統和設備的運行,需要對模型進行不斷更新,這為基于模型的故障診斷帶來嚴峻挑戰。基于數據的故障診斷方法無需獲取系統的精確模型,并且可從運行數據中挖掘系統運行狀態信息。

然而,開展高超聲速飛行器故障診斷實驗的難度大、危險性高,因此實際中往往面臨著高超聲速飛行器故障數據缺失的情況,為數據驅動的故障診斷方法帶來困難。利用模型仿真結果生成高超聲速飛行器故障數據集,基于此訓練的機器學習模型可作為故障診斷預訓練模型,為高超聲速飛行器實際故障診斷提供重要基礎。當可獲取高超聲速飛行器實際運行數據時,可更快實現故障診斷模型的更新。

考慮到運行狀態數據會受到強噪聲和非高斯噪聲的影響,為實現強噪聲下的高超聲速飛行器迎角傳感器故障診斷,本文采用了分數階混沌系統設計噪聲抑制方法和信號特征提取方法。本文所提出的故障診斷框架如圖2所示。

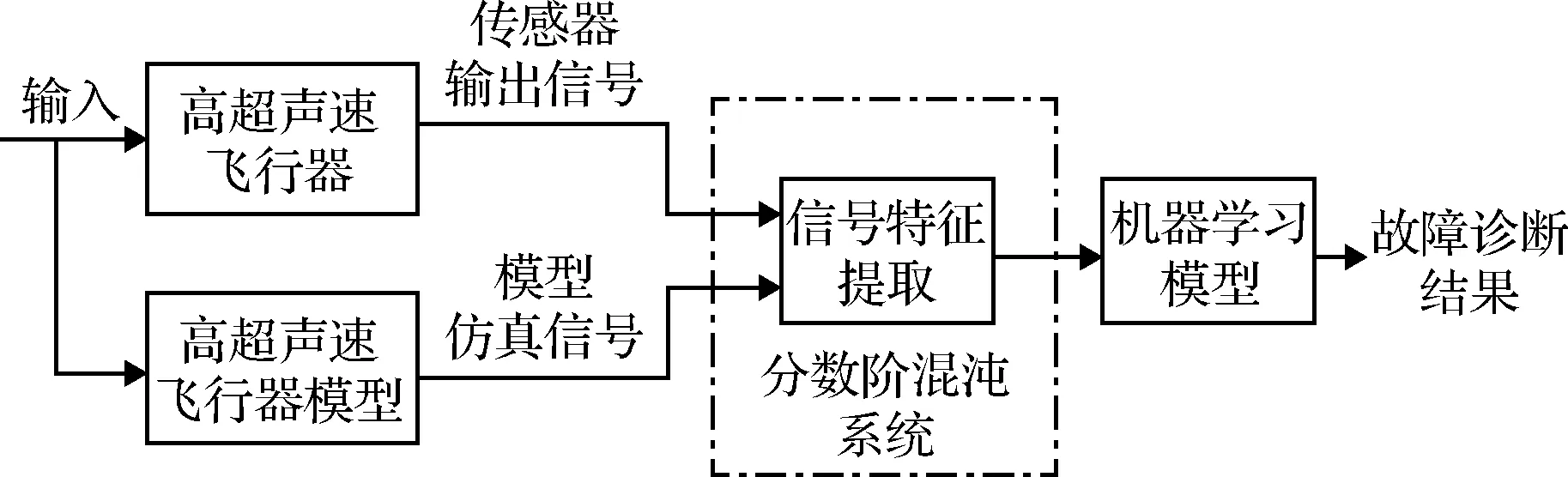
圖2 基于分數階混沌系統和機器學習模型的高超聲速飛行器迎角傳感器故障診斷方案Fig.2 Fault diagnosis scheme of the AOA sensor based on fractional-order chaos system and machine learning

2.1 基于分數階混沌系統的信號特征提取

復雜的飛行環境會使得故障信號特征淹沒在強噪聲中,這是高超聲速飛行器故障診斷所面臨的主要挑戰,從含噪聲信號中提取故障信號特征是提高故障診斷準確率的有效手段。為在實際工程中應用混沌系統的噪聲免疫性質,以分數階Lorenz混沌系統為基礎,本文利用分數階系統的穩定性設計了一種可同時處理高斯噪聲和非高斯噪聲且無需獲取或假設其概率密度分布等信息的信號處理方法。

Duffing系統需要合適的外部信號激勵才能達到混沌狀態,因此Duffing系統常常被用于微弱信號檢測。然而Duffing系統可檢測的信號類型有限,并且在信號檢測過程中需要復雜的調節過程,在實時性要求高且待測信號復雜的情況下,基于Duffing系統的信號檢測方案受到較大的限制。因此考慮對分數階Lorenz系統進行改進,使其一方面可接收外部信號,并可在外部待測信號的激勵下出現相變,達到混沌狀態,以使得系統擁有噪聲免疫特性。另一方面則需要其在一定參數的控制下呈現可控的系統相變,實現信號檢測。

傳統的分數階Lorenz混沌系統的數學模型為

(8)

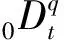
(9)

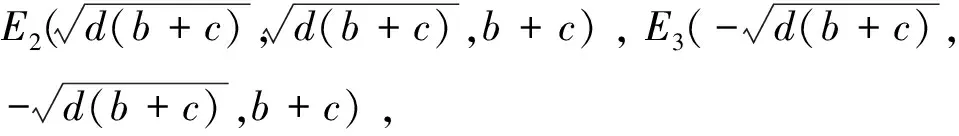
(10)

雅可比矩陣在平衡點E2和E3處的特征值為

(11)

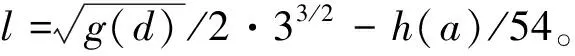
引理 1.對于階次為q的分數階系統,若其雅可比矩陣在某平衡點處的所有特征值滿足[16]:

|arg(λj)|>qπ/2,j=2,3

(12)

則該平衡點是漸近穩定的,其中,arg(·)表示復數的輻角。

引理3.對于一個分數階系統,假設其鞍焦點的某個不穩定特征值為λ=o+ei,其中,o和e分別表示其實部和虛部,則使得該分數階系統存在雙渦卷混沌吸引子的必要條件為該鞍焦點處于系統不穩定域[16]。

定理1.對于分數階系統(9),若系統參數條件:

(13)

成立,且分數階階次條件:

(14)

成立,則系統為非混沌狀態,且存在兩個指數2的鞍點和一個指數1的鞍點。式(14)中,real(·)表示復數的實部。

證.當分數階系統參數滿足條件(13)時,根據引理2,平衡點E1為指數1的鞍點,平衡點E2和E3為指數2的鞍點,根據引理1和引理3,當分數階階次滿足(14)時,則分數階系統混沌的必要條件不滿足,系統處于非混沌狀態。證畢。

Lyapunov指數描述了系統相空間中差異極小的兩條相近軌道隨時間分離的速度。它的數學定義為

(15)

式中:標量參數LE表示系統Lyapunov指數。若系統存在正的Lyapunov指數,則說明系統是混沌的。

根據定理1,系統參數可以設置為:a=7,b=7,c=-2,d=9/4。系統階次可設置為q=0.96,此時系統(9)的Lyapunov指數為:-6.443,-0.337,-0.297,系統(9)為漸近穩定的,其狀態如圖3所示。

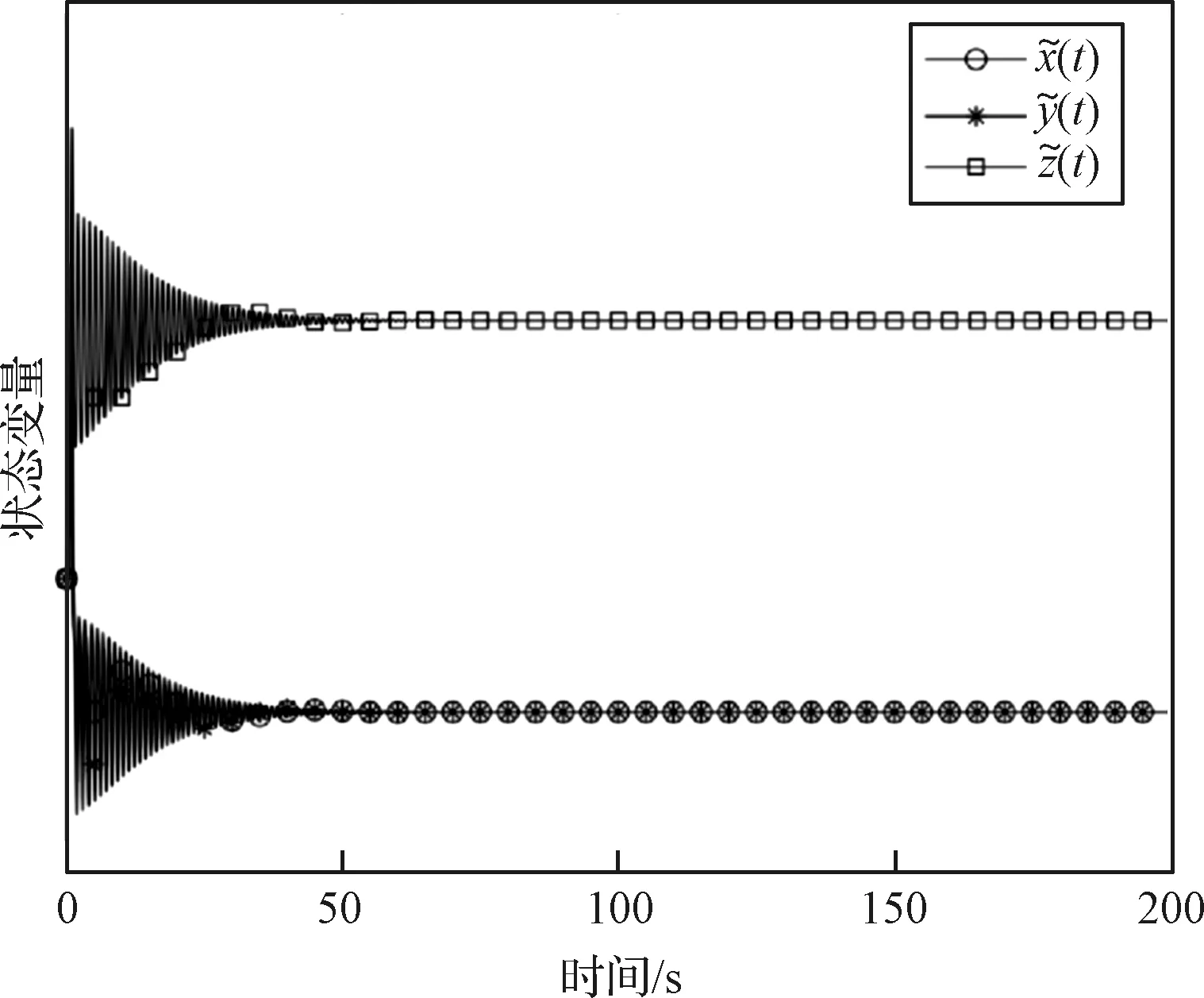
圖3 q=0.96時Lorenz系統狀態曲線Fig.3 The system state signals in time domain when q=0.96

采用Lyapunov指數的方法分析外部輸入信號Gr(t)對系統動力學行為的影響。令r(t)=1,令信號增益G在區間[0,40]內連續變化,系統Lyapunov指數如圖4所示。

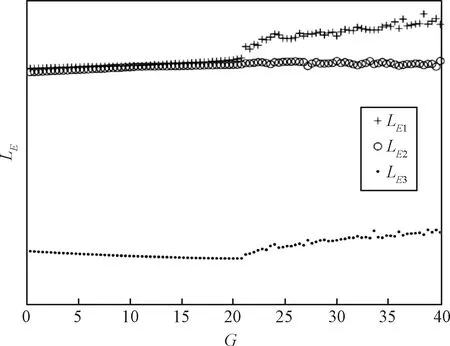
圖4 在Gr(t)激勵下的系統Lyapunov指數Fig.4 The Lyapunov exponents of the system under the excitement of signal Gr(t)

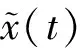
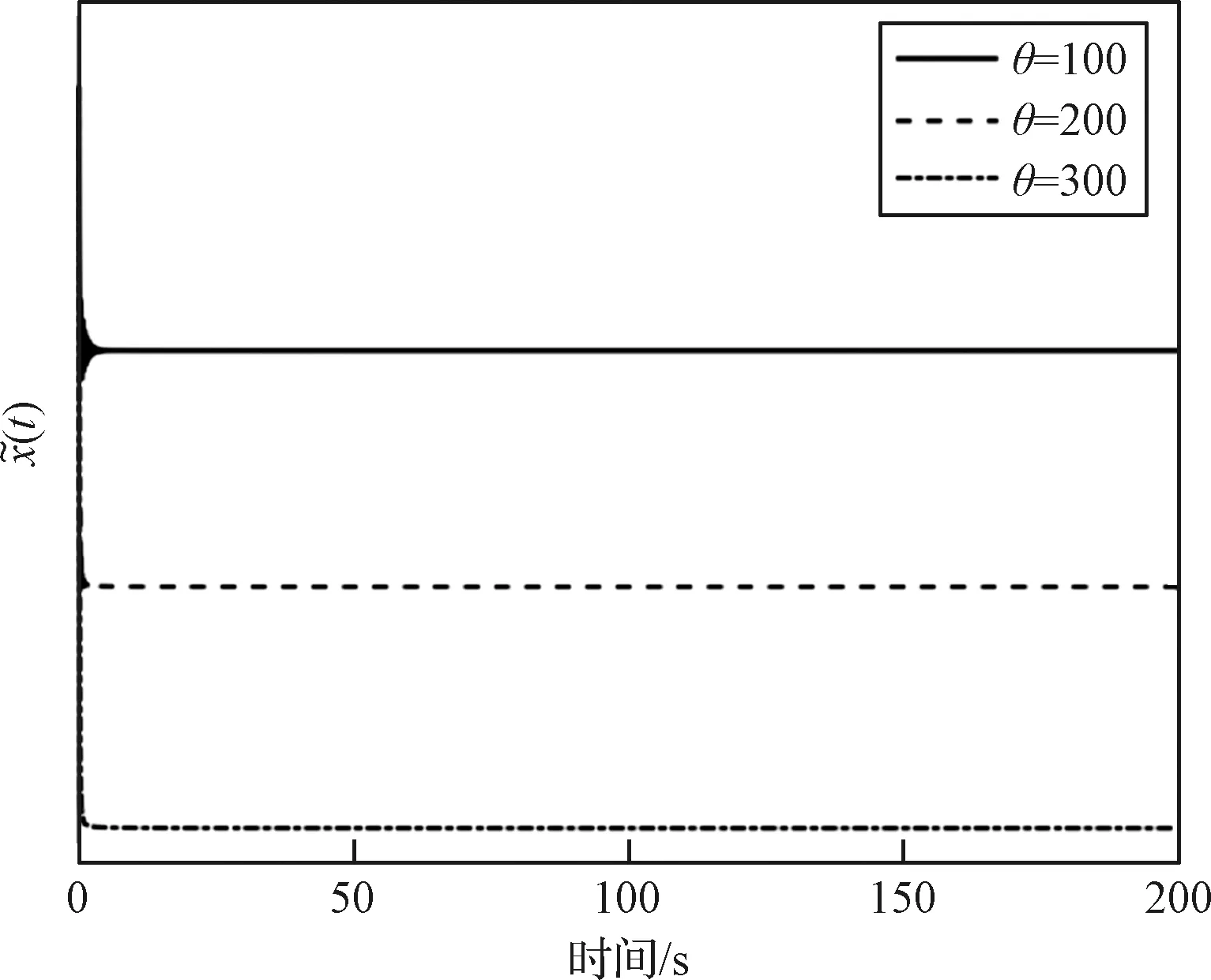
圖5 在參數θ影響下的系統狀態曲線Fig.5 The system state signals under the influence of θ

系統平衡狀態和參數θ的關系可表示為:

(16)

其中函數C(·)表示系統(9)的非線性混沌映射,Ξx,Ξy和Ξz分別表示系統三個狀態變量達到穩定狀態時的值。進一步,根據式(16)可得,改進的分數階Lorenz系統的系統狀態分為兩部分,穩定狀態和由外部信號激勵引起的震蕩,即:

(17)

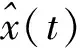
(18)

2.2 基于機器學習的故障診斷模型構建

由于高超聲速飛行器實際運行故障數據獲取難度大,因此難以開展基于數據驅動的故障診斷方法研究。在實際中,由于高超聲速飛行器運行環境較為復雜,基于模型的故障診斷也面臨著諸多局限性。因此,以模型仿真為基礎,構建高超聲速飛行器故障數據集,并以此構建迎角傳感器故障診斷分類器,并可作為高超聲速飛行器故障診斷的預訓練模型。

所提出的基于混沌系統的信號處理方法能抑制噪聲的影響,從而實現故障信號提取的目的,可有效提升故障診斷的準確性。

首先利用模型仿真構建高超聲速飛行器迎角傳感器故障數據集,每種故障類型生成1 000條樣本數據,在每種故障類型的樣本中隨機抽取500個樣本注入高斯噪聲,其余樣本則注入拖尾噪聲(7),并使注入高斯噪聲樣本信號信噪比為RSN=-2,注入拖尾噪聲的樣本信號信噪比為RSN=-1。

采用隨機數使得每個樣本的故障大小均不相同,分別表現為數據偏離大小不同、增益變化程度不同、異常值大小不等。在每組故障中,設置了三種不同的故障出現時間。對于異常值故障,每個樣本設置的異常值出現時間和出現次數均不同。該數據集信息如表1所示。

表1 迎角傳感器故障數據集信息Table 1 Information of the angle of attack sensor fault datasets

為保證所設計故障診斷算法的實用性,考慮到高超聲速飛行器系統的實際算力,本文采用三種機器學習模型構建故障分類器:徑向基核函數支持向量機、隨機森林和基于AdaBoost集成的決策樹。其中支持向量機采用徑向基核函數,其模型為

(19)

式中:s1和s2表示樣本特征向量;δ為可調的超參數。設隨機森林規模為100,它可表示為

(20)

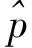
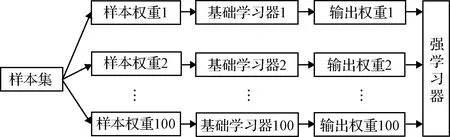
圖6 Adaboost算法流程圖Fig.6 Flowchart of the Adaboost algorithm

3 仿真校驗

為驗證所提出基于分數階混沌系統的信號處理方法的有效性,由于所構建的故障數據集同時包含高斯噪聲和非高斯噪聲且噪聲功率較大,為驗證所提出的故障特征提取算法的有效性,本節設置了三組對照實驗:第一組利用原始數據集對機器學習模型進行訓練。第二組采用小波方法對原始信號進行濾波處理,并用小波處理后的數據訓練機器學習分類器。第三組利用所提出的基于分數階混沌系統的信號處理方法對原始數據進行故障信號特征提取,再用處理后的樣本對機器學習模型進行訓練。

根據所設計的基于分數階混沌系統的信號處理方法,考慮到故障信號的幅值大小以及高斯噪聲的功率,為實現故障信號特征提取,設置信號增益為G=20,令分數階混沌系統(9)的控制參數為θ=200。考慮注入拖尾噪聲的樣本信號的幅值,設置信號增益為G=20,令分數階混沌系統(9)的控制參數為θ=400。圖6和圖7展示了一組樣本處理前和處理后的結果。

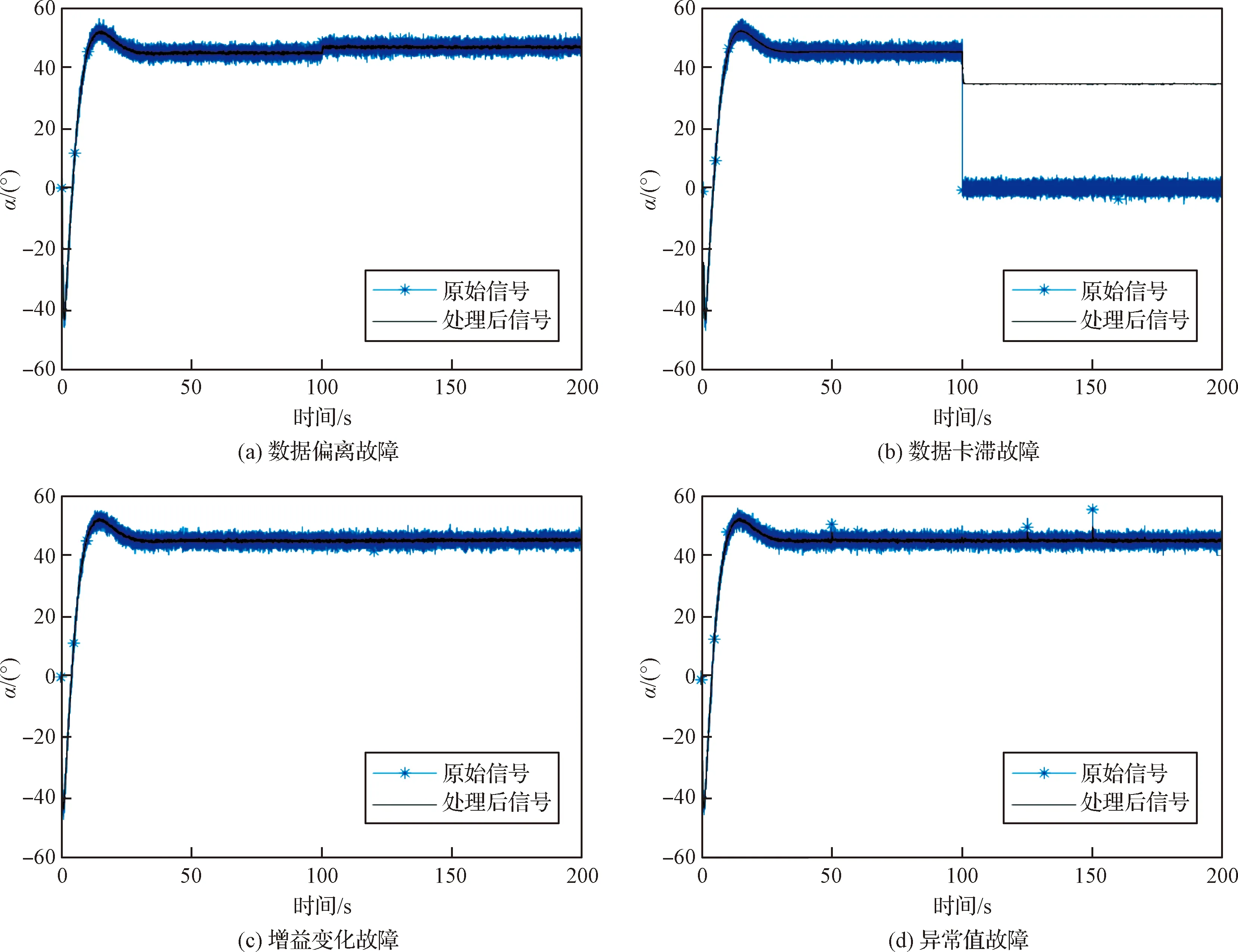
圖7 高斯噪聲下待測信號和提取的故障信號Fig.7 The signals to be detected and the extracted fault signals under Gaussian noise

從圖7和圖8中可以看出,強噪聲的存在不僅會掩蓋故障特征,還會使得不同類型故障的樣本具有較大的相似性。例如在強噪聲下,傳感器異常值會被噪聲掩蓋,在非高斯噪聲下,數據偏離故障、增益變化故障和異常值故障等表現出較大的相似性。由于分數階混沌系統的噪聲免疫性,通過所設計的基于分數階混沌系統的信號特征提取方法,可有效地降低強噪聲的影響。

按照8∶2的比例將故障樣本集隨機劃分為訓練集和測試集,并對機器學習模型進行訓練,在原始數據集上,支持向量機、AdaBoost集成模型和隨機森林模型在測試集上的總體分類準確率分別為:95.5%、89.25%和95.25%。然后采用分解尺度為3的啟發式小波閾值函數方法對原始信號進行濾波處理,并用濾波后的數據訓練模型,得到的分類器在測試集上的準確率分別為:97.5%、90.75%和97.75%。

最后利用所提出的基于分數階混沌系統的信號處理算法對故障樣本進行處理,用該數據訓練的分類器在測試集上的總體分類準確率分別提升到了:99.5%、96.25%和98.75%。

三種模型在各故障類型上的分類準確率(%)和召回率(%)見表2。其中,故障1、故障2、故障3和故障4分別代表數據偏離故障、卡滯故障、增益變化故障和異常值故障。由于卡滯故障(故障2)的故障特征明顯,無論在信號處理前和處理后都能得較高的準確率和召回率。其它故障特征較小并難以提取,從而影響該類故障的診斷。通過小波濾波后,可提高故障分類的準確率和召回率。在強高斯噪聲、非高斯噪聲的影響下,增益變化故障、異常值故障和數據偏離故障表現出極大的相似性,采用本文所提出的基于分數階混沌系統的信號處理方法,可有效提取故障特征,取得了比小波濾波更好的效果,提升了故障診斷準確率。

表2 信號處理前后的故障診斷結果對比Table 2 Comparison of the fault diagnosis results before and after signal processing 單位:%

4 結論

針對高超聲速飛行器迎角傳感器易出現故障且易受強噪聲影響的問題,本文提出了一種基于分數階混沌系統的信號處理方法與一種結合系統模型和機器學習模型的故障診斷方法。以自治的Lorenz混沌系統為基礎,根據分數階系統穩定性對其分數階階次和系統參數進行了設計,并設計了一種信號處理方法,由于分數階混沌系統的噪聲免疫特性,所提出的信號處理方法可用于強高斯噪聲和強非高斯噪聲下的故障信號提取。基于高超聲速飛行器的系統模型構建了飛行器迎角傳感器故障樣本集,并用于機器學習模型的訓練和迎角傳感器故障診斷。仿真實驗結果表明,所提出的信號處理方法可有效提取信號特征,提升故障診斷準確率。