基于數學模式的數學競賽中不等式問題的探究

湖南師范大學數學與統計學院(410081) 黃慧萌 吳仁芳

有關數學模式的說法,源于對數學本質的探究. 鄭毓信指出對于數學學科來講,模式對于數學具有特殊的意義,可以說,數學的本質即是關于數學模式的科學[1],于文華將數學模式分為存在于記憶中的數學模式和作為知識的數學模式[2]. 喻平解釋說數學模式是指形式化的采用數學語言,概括的或近似的表述某種事物系統的特征或數量關系的一種數學結構[3-4]. 目前許多著名科學家已認可數學是一門研究模式的科學,可見數學模式對于問題解決具有重要意義.

數學競賽歷史悠久,它首先是由匈牙利發起的,匈牙利也通過數學競賽培養了一批優秀的數學家,開展數學奧林匹克競賽活動有助于提高青少年的數學探索能力,進一步提高人才的數學素質[5]. 數學競賽涉及數學學科的各個知識點,而不等式問題在數學競賽中占據重要地位. 基于競賽試題及相關文獻,解決不等式問題的常用方法有以下八種,即構造函數法、變量代換法、引入參數法、比較法、放縮法、反證法、數學歸納法以及利用重要不等式證明不等式問題[6].

著名教育家徐利治教授提出RMI 原理[7],即關系映射反演原理,它的操作主要依賴于化歸,即將復雜的問題通過映射化為簡單的問題,然后求得簡單問題的解,再通過逆映射(反演)求得原來復雜問題的解,基本步驟可歸納為:“關系——映射——定映——反演——獲解”,其關鍵在于在兩個重要的關系結構中構造出合適的映射. RMI 原理是化歸原則的更高層次,對數學研究具有重要的指導意義[8]. 因此,本文在了解數學競賽中不等式問題常用方法的“個性”后,以RMI 原理為理論依據,尋求這些方法的“共性”,化難為易,對于學生減輕記憶負擔,深刻認識并掌握這些方法具有重要意義. 最后,從數學模式的角度探究,給出了數學競賽中不等式問題的四種數學模式,即構造法模式、變量代換模式、引入參數模式、數學模型模式. 其中構造法模式包括構造函數模式、構造對偶式模式、構造數列模式、構造圖形模式;數學模型模式包括應用柯西不等式模式、應用均值不等式模式、應用琴生不等式模式、應用伯努利不等式模式.

一、構造法模式

構造法模式主要包括構造函數模式、構造對偶式模式和構造數列模式. 構造法模式是不等式證明中的一種重要數學模式,主要利用引入恰當的函數、對偶式、數列、圖形等輔助手段,使命題轉化,變成較為容易證明的形式.

1. 構造函數模式

構造函數模式是指根據所給代數式的特點,結合題目所給條件,構造出適當的函數,并且結合函數的單調性等性質來解決不等式問題的一種數學模式.

例1(2020 年摩爾多瓦國家隊選拔試題)已知a,b,c是正實數,求證

證由柯西不等式可得則u≥1

故f(x)在[1,+∞)上單調遞增,從而f(u)≥f(1)=結合(1)式可得

評注該題結合題目所給條件,構造出一個函數,并通過求導判斷函數單調性,利用該函數在定義域內單調遞增,繼而求得函數的最小值,不等式便得證.

2. 構造對偶式模式

構造對偶式模式指根據題中某式A的結構特征,構造出A的對偶式B,再利用A與B之間的運算求得A、B的兩種關系式,從而使問題獲得解決的數學模式. 一般來說,構造對偶式模式常常用在一些輪換不等式的證明問題中,通過構造出的不等式與原來的不等式結合考慮,易于簡化問題.

例2設xi >0(i=1,2,··· ,n)且求證:

證明令不等式左邊為A, 其對偶式由平均不等式可得:

評注該題通過構造不等式左邊的對偶式,再進行原式及其對偶式間的加、減運算,借助平均不等式,化難為易,繼而順利解決問題.

3. 構造數列模式

構造數列模式指根據題目所給式子的特征,通過構造輔助數列,再利用數列的性質,如單調性來解決不等式問題的數學模式. 構造法模式常用在與n有關的不等式問題中.

例3(2021 年加拿大數學奧林匹克試題) 已知n是給定的不小于2 的正整數, 設正實數a1,a2,··· ,an滿足a1+a2+···+an=2n-1,求

的最小值.

當ai=2i-1(i=1,2,··· ,n)時,上式可取到等號,故所求最小值為n.

評注該題是不等式問題中的求值問題,要求所給式子的最小值,即證原式大于等于一個常數即可. 可通過構造輔助數列,并令數列首項為1,得到數列前n項和Sn的表達式,以此為切入口. 繼而借助an=Sn -Sn-1,將原式中an用Sn-Sn-1代替,最后利用均值不等式解決問題.

4. 構造圖形模式

構造圖形模式是指根據題目所給條件中的數量關系的幾何意義構造圖形的數學模式. 一般說來,構造圖形可使題目中的條件和結論之間的關系更加直觀,問題便得以簡化.

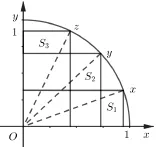
圖1

例4設x,y,z為實數,0

證明原不等式等價于>sinx(cosx-cosy) +siny(cosy-cosz) + sinzcosz, 故構造圖形如圖1 所示,圓O是單位圓,S1,S2,S3分別是三個小矩形的面積, 則S1= sinx(cosx-cosy),S2= siny(cosy-cosz),S3=sinzcosz. 由于S1+S2+S3<故有>sinx(cosx-cosy)+siny(cosy-cosz)+sinzcosz,故原不等式成立.

評注該題通過構造單位圓,將題設條件轉化為單位圓中三個小矩形的面積,化代數關系為幾何,最終證明不等式.

二、變量代換模式

變量代換模式指將一個較復雜的式子視為一個整體,用一個字母代換它, 從而將復雜問題簡單化的一種數學模式.也就是說,變量代換模式通常是通過變換代數式的形式,以顯示其內在結構的本質,它常常能將無理式化為有理式,將分式化為整式.

例5(2021 年以色列數學奧林匹克試題)如果a,b,c是非負實數,那么

證明設x=a2+ab+b2,y=b2+bc+c2,z=c2+ca+a2,p=q=a2+b2+c2,r=ab+bc+ca,則x+y+z=p+q+r,故原式等價于

所以xy+yz+zx≤pq+qr+rp. 不妨設a=min{a,b,c},b=a+x,c=a+y(x,y≥0),則

其中A=x2- xy+y2≥0,B= 3(x-y)2(x+y) +11(x3+y3)>0,C= 3(x2-y2)2+ 5(x4+y4)+5xy(x2+y2)≥0,

所以xyz≤pqr, 由對稱函數定理可知:故原式得證

評注該題主要利用換元的思想,將題目所給的復雜式子用一個字母代替,化難為易,最后結合對稱函數定理,順利解決問題.

三、引入參數模式

引入參數模式是指在不等式的證明中恰當引入參數與運算,使其達到預定的目的的一種數學模式. 引入參數模式是不等式證明中的一個高級技巧,往往能使復雜問題簡單化.

例6(2019 年加拿大奧林匹克試題)設n >1 為整數,a0,a1,a2,a3,··· ,an,k為實數, 且a1=an-1= 0, 證明

證明易知方程x2-kx-1 = 0 存在兩個不等的實根,且由兩根之積等于-1,必有一根的絕對值不小于1,不妨設這一根為t,則|t|≥1,于是t2-kt-1=0,因此對任意的i ∈{0,1,··· ,n-2},有

注意到a1=an-1=0,從而

評注該題通過引入參數,令再將該參數代入所證式子中并結合絕對值不等式,再通過具體運算,不等式便得證.

四、數學模型模式

從廣義上說,數學中各種基本概念、各種公式、定理以及各種算法系統都可稱之為數學模型. 一些重要的不等式如柯西不等式、均值不等式、琴生不等式、伯努利不等式是解決數學競賽中不等式問題的重要輔助手段. 因此,數學模型模式是指利用四個重要不等式解決實際問題的一種數學模式.

1. 應用柯西不等式模式

柯西不等式的一般形式為: 對任意的a1,a2,··· ,an,b1,b2,··· ,bn,有

當且僅當ai,bi(i= 1,2,···n) 中有至少一方全為零或時等號成立.

應用柯西不等式模式是指以柯西不等式為切入口,解決不等式問題的一種數學模式. 柯西不等式作為數學競賽中的重要考查內容之一,除被直接利用外,它的一些變式及推論也對解決不等式問題助益頗多.

例7(2020 年摩爾多瓦國家隊選拔試題)已知a,b,c是正實數,求證

證明由柯西不等式可得√7a+b+c, 即從而同理可得故要證原不等式成立,只需證

根據柯西不等式,可得

從而原不等式成立.

評注該題兩次運用柯西不等式,第一次運用柯西不等式將原不等式進行轉化,從而使題目結構得以簡化,接著再次運用柯西不等式,再加以運算簡化,最終不等式得以證明.

2. 應用均值不等式模式

均值不等式的一般形式為: 對任意的正數a1,a2,··· ,an,都有

當且僅當a1=a2=···=an時成立.

應用均值不等式模式指以均值不等式為出發點解決不等式問題的數學模式,均值不等式是在中學數學中最常用到的一個重要不等式,中學中的基本不等式就是其中一個重要的特例,掌握應用均值不等式模式對求解不等式試題有重要的意義.

例8(2019 年全國高中數學聯賽試題) 設正實數a1,a2,··· ,a100滿足ai≥a101-i(i=1,2,··· ,50),記xk=(k=1,2,··· ,99),證明

證明注意到a1,a2,··· ,a100>0,對k= 1,2,··· ,99,由均值不等式知

從而有

記(2)的右端為T,則對任意i= 1,2,··· ,100,ai在T的分子中的次數為i-1,在T的分母中的次數為100-i,從而

又0 ≤a101-i≤ai(i= 1,2,··· ,50), 故T≤1, 結合得

評注該題首先結合題目所給條件, 用a1,a2,··· ,a100將要證式子進行替換,再利用均值不等式,可將式子轉化為ai(i=1,2,··· ,100)的冪次方的乘積,最后得以證明.

例9(2020 年德國數學奧林匹克試題)設n為給定的正整數,正實數a,b,c滿足求

證明由柯西不等式可得

即(a2n+1+b2nc+bc2n)≥(an+bn+cn)2,同理可得

因此

評注該題先利用題設條件將式子乘以即乘以一個等于1 的數,式子不變,再以柯西不等式為突破口,結合均值不等式,順利求得式子的最大值,解決問題. 由該題可知,這些重要不等式常常需要綜合運用,方能高效解決不等式問題.

3. 應用琴生不等式模式

琴生不等式(加權)形式為:對任意的x1,x2,··· ,xn ∈[a,b], 且a1+a2+···+an= 1,a1,a2,··· ,an為正數, 若f(x)是[a,b]上的下凸函數,有

f(a1x1+a2x2+···+anxn)≤a1f(x1)+a2f(x2)+···+anf(xn),

若f(x)是[a,b]上的下凹函數,則有

f(a1x1+a2x2+···+anxn)≥a1f(x1)+a2f(x2)+···+anf(xn).

當且僅當x1=x2=···=xn時等號成立.

應用琴生不等式模式是指以琴生不等式為輔助手段,解決不等式問題的一種數學模式. 其具體操作為通過觀察題目特征,二次求導判斷題設函數為下凸函數還是下凹函數,再結合琴生不等式解決問題.

例10(2020 年第61 屆IMO 試題)正實數a,b,c,d滿足a≥b≥c≥d,并且a+b+c+d=1,求證:

證明問題等價于

由于因此由琴生不等式

因此,只要證

或

即可,由于

因此,結論成立

評注該題首先對不等式兩邊取對數,將問題進行等價轉化,再利用琴生不等式,對所形成的新式子進行進一步轉化,接著進行運算,最后不等式便得以證明.

4. 應用伯努利不等式模式

伯努利不等式的一般形式為:若實數xi(i=1,2,··· ,n)各項符號相同,且xi >-1,則

(1+x1)(1+x2)···(1+xn)≥1+x1+x2+···+xn.

應用伯努利不等式模式指以伯努利不等式為切入口,繼而解決不等式問題的一種數學模式. 對于數學競賽中的不等式問題,常常通過題設條件,判斷其符合伯努利不等式運用的條件后,將其運用,最后使復雜問題簡單化.

例11已知正實數x,y滿足x+y2016≥ 1, 證明

證明當時,由伯努利不等式,得而y >0,所以x2016+y >1-

當0

下面證明

事實上,由伯努利不等式,有

評注該題首先將要證不等式左邊進行分拆為x2016及y, 再分別利用伯努利不等式證明x2016和y分別大于因此二者之和顯然大于故不等式得證.

五、結語

數學競賽中不等式問題的常用解法有許多種,在了解這些解法各自特點的基礎上,挖掘這些解法的“共性”,有利于學生進一步認識這些基本方法, 厘清這些基本方法的本質,提高他們分析和解決問題的創新能力. 利用徐利治教授提出的RMI 原理,可以歸納出一類具有相同基本思想的數學模式,即借助熟悉的結構或已有定理,將復雜問題轉化為簡單問題,化生為熟,以簡馭繁. 因此,本文以RMI 原理為理論依據, 結合數學競賽中不等式問題常用方法并以此為切入口,對不等式問題進行模式劃分,給出了四種數學模式,具體為構造法模式、變量代換模式、局部調整模式、數學模型模式.當問題解決者面對數學競賽中不等式問題時,首先應仔細分析題目所給條件,觀察原有式子的結構特征,從題干出發分離出與之相關的數學模式并選擇適配的解題方法,以此獲得問題的最佳解法.