汽車電動遮陽簾結構分析及系統阻力研究

唐榮華 王占 黃旸 王林 王琛

（廣州汽車集團股份有限公司汽車工程研究院，廣州 511434）

1 前言

天窗是車身系統中最大的機電一體化總成件之一。固定式全景天窗具有大尺寸、廣視野、低成本、高可靠性以及可提供舒適的頭部空間等優點，近年來應用廣泛，與可開啟式全景天窗相同，為解決車內遮光與隔熱問題，需同時搭載遮陽簾[1-2]，隨著車頂視野的不斷增大，遮陽簾的開口尺寸也不斷增大，并成為新的獨立總成件，其布置形式、結構方案越來越豐富，技術難度也越來越高。

目前，國內對汽車電動天窗的機構運動、防夾與控制方面的研究較多[3-5]，蔣菲等[6]介紹了遮陽簾的硬挺整理工藝，提供了滿足使用要求的簾布參數，李海帆等[7]提出了遮陽簾的同步驅動技術，新的結構使遮陽簾的張力更穩定。但是，汽車電動遮陽簾方面的獨立研究很少，尤其缺乏對遮陽簾的系統研究。

本文對汽車電動遮陽簾進行結構分析，建立電動遮陽簾的基本模型，對遮陽簾展開與收卷過程中的運動部件進行詳細受力分析，得到遮陽簾在運動過程中的受力狀態與遮陽簾位置的關系，從而建立遮陽簾的系統阻力與其開口尺寸的數學表達式，識別影響各部件受力的潛在因素。

2 遮陽簾結構及其工作原理

2.1 遮陽簾的基本結構

遮陽簾的結構類型多樣，但均采用口字型框架結構，主要由支撐框架、遮陽系統、驅動系統及控制系統組成。其中，支撐框架包括前梁、后梁、左/右導軌、軟軸回管、軟軸與滑塊，遮陽系統包括卷軸、簾布、邊條與拉桿，驅動系統與控制系統集成在電機總成上，如圖1所示。

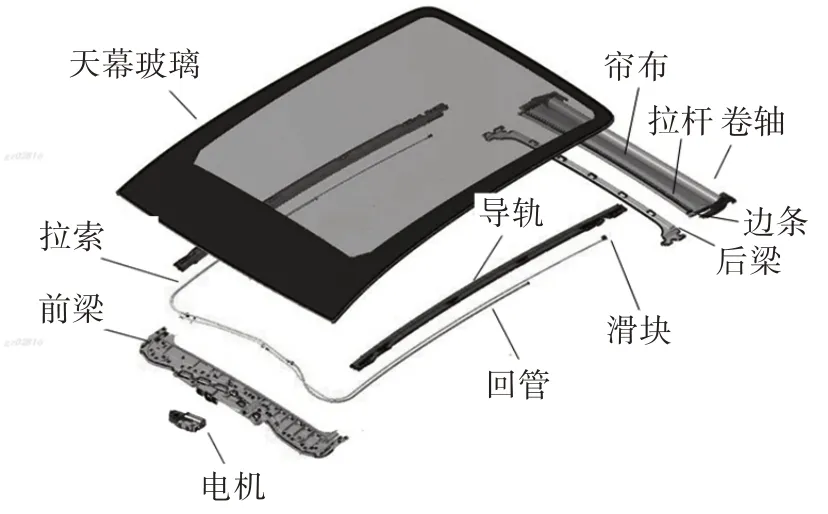
圖1 汽車電動遮陽簾結構爆炸圖

2.2 遮陽簾的工作原理

汽車電動遮陽簾總成典型結構如圖2 所示，邊條與簾布Y向連接，一端連接滑塊，一端連接卷軸，整體嵌入兩側導軌的邊條槽內，簾布受Y向張力達到繃緊狀態，如圖3 所示。在X方向，簾布一端連接拉桿，一端連接卷軸，在卷軸卷收力作用下，簾布X向受力達到繃緊狀態，如圖4 所示。簾布周圈均受張力而均勻展開在支撐框架內，關閉狀態時，拉桿處于m位置，對應軟軸區間為a-b-c-d-e-m，打開狀態時，拉桿處于n位置，對應軟軸區間為g-d-e-n。

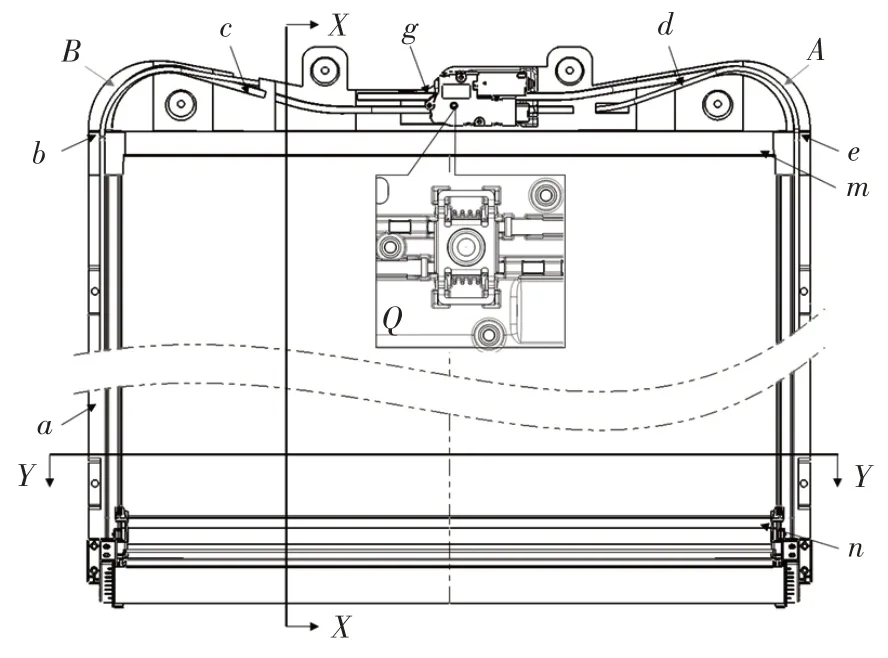
圖2 遮陽簾總成結構原理

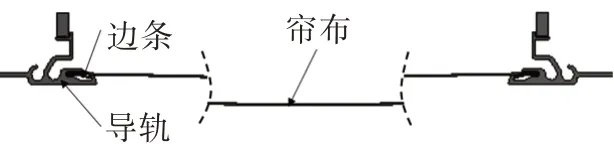
圖3 遮陽簾Y向張緊示意

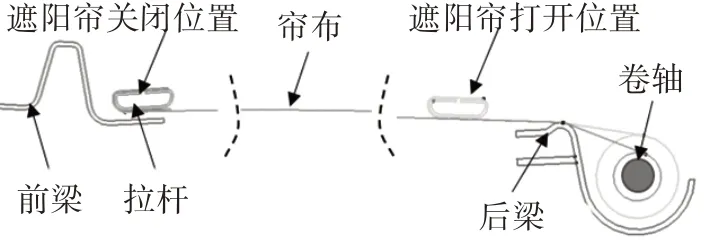
圖4 遮陽簾X向張緊示意

電機在Q處通過齒輪與軟軸嚙合，在控制系統的指令下運轉，帶動軟軸在滑槽內線性移動，從而通過控制電機的轉動來實現遮陽簾的開閉運動。根據遮陽簾的運行過程分析，汽車電動遮陽簾基本結構件及其約束類型如表1所示。

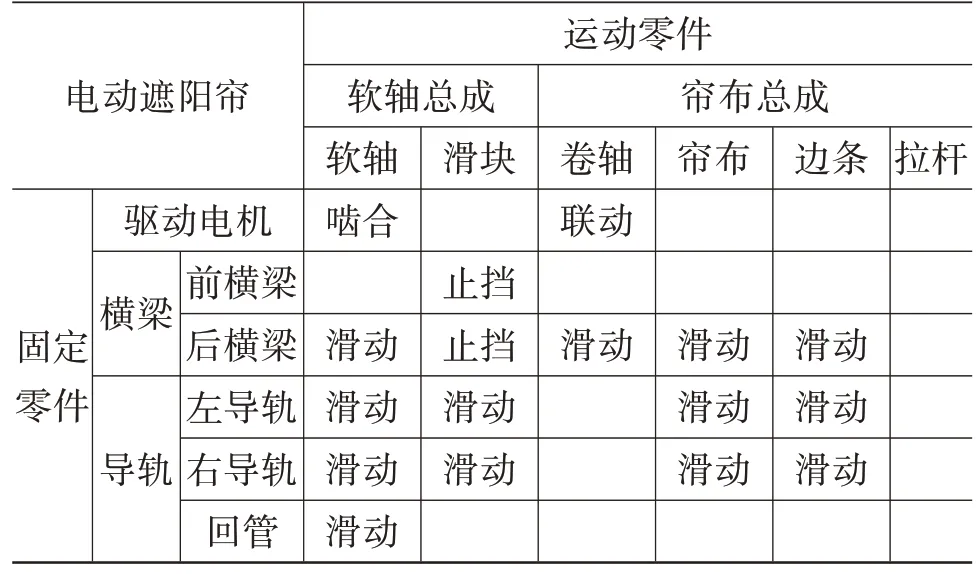
表1 汽車電動遮陽簾基本結件及其約束類型

3 遮陽簾運行部件受力分析

本文研究的電動遮陽簾結構見圖2，相關參數如下：Y向開口為830 mm，X向行程為1 200 mm，簾布面密度為280 g/m2，最大出布角為30°，軟軸轉角曲率半徑約為90 mm，轉角圓弧處包角為90°，軟軸長為1 880 mm，直徑為4.7 mm，線密度為80 g/m，邊條支撐角度α=arctan0.5，邊條與簾布厚度相等且均為0.6 mm，摩擦因數統一取為0.2，卷軸桿外徑為20 mm，卷軸彈簧實測剛度為0.06 N·mm/(°)，簾布初拉力為(15±5) N。基于以上參數與電動遮陽簾三維數據，并結合表1，對遮陽簾5個基本運動子件進行受力分析。

3.1 軟軸受力分析

軟軸是遮陽簾運動過程中的關鍵傳動部件，受到多個復合力的作用。以單側軟軸為例，遮陽簾在運行過程中軟軸受力可分解成滑槽摩擦力fm、轉角A處的軟軸擠壓帶來的阻力fA與轉角B處的軟軸自由端變形帶來的阻力fB。

軟軸在導軌、導槽及回管內的運動方式等同于線纜在管道內的運行模型[8]，如圖5 所示，其中V為軟軸的運動方向，得到軟軸直線段平衡方程為：

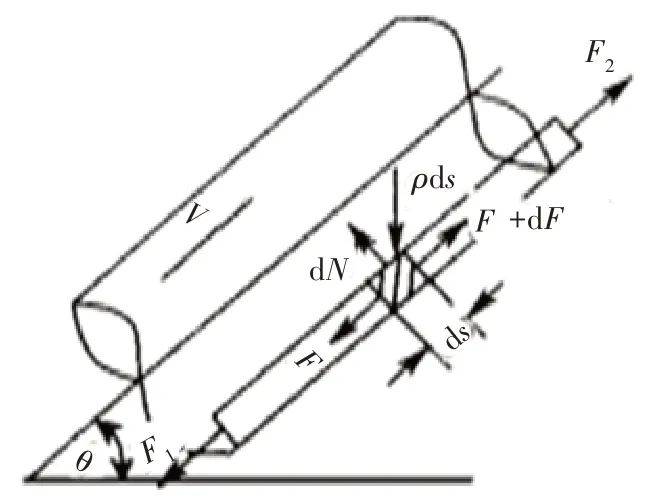
圖5 軟軸在直線段的運動受力簡圖

式中，θ為導軌與水平面夾角；μ1為軟軸與導軌的滑動摩擦因數；ρ為軟軸的線密度；F為單位長度軟軸所受初始張力；dN為單位長度軟軸所受支撐力；ds為單位軟軸的長度；dF為單位長度軟軸的驅動力。

合并式（1）與式（2）求積可得：

式中，F2為軟軸驅動端受力；F1為軟軸從動端受力；S為軟軸驅動端到從動端的長度。

由式（3）可知，軟軸在滑槽內的移動與運動方向無關，與軟軸長度線性相關。根據樣件尺寸，求得軟軸在滑槽內的摩擦力為：

經計算，fm=0.3 N。

軟軸在轉角A處的運動受力如圖6 所示，忽略圓弧處軟軸的質量，得到軟軸全包角處的平衡方程為：

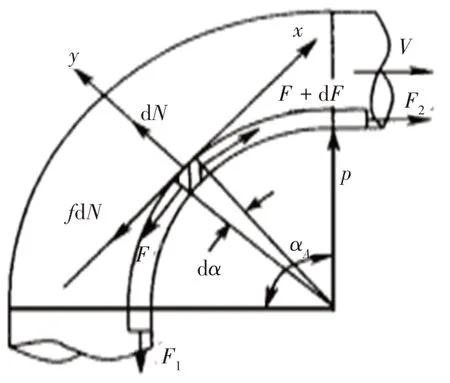
圖6 軟軸在轉角A處的運動受力簡圖

式中，αA為圓弧包角；μ2為軟軸與軟軸槽的滑動摩擦因數。

由式（5）和式（6）可得：

由式（7）可知，軟軸在轉角A處所受阻力與軟軸轉彎半徑無關，與所經過彎道的包角和軟軸摩擦因數相關。根據樣件結構及其尺寸參數，Q處軟軸的嚙合力FQ等于遮陽簾系統阻力，可得軟軸在轉角A處的拉拽力fAL與推送阻力fAT分別為：

經計算，fAL=0.27FQ，fAT=0.37FQ。

軟軸在轉角B處的運動受力簡圖如圖7 所示，等效一端固定的圓柱懸臂梁末端受力產生變形的過程[4]。圓弧包角αB為變量，沒圓弧中心半徑為q，軟軸末端受管壁正壓力為FB，軟軸的圓柱形截面慣性矩I=πd4/64，軟軸彈性模量EZ=16.3 GPa，軟軸末端導向頭長度為10 mm，末端懸臂長度為L=q·sinαB+10，軟軸末端變形量為ω=-q(1-cosαB)，且不計圓弧處軟軸的質量，得到軟軸末端的撓度方程為：

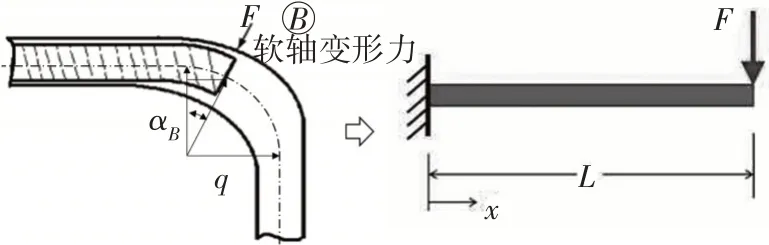
圖7 軟軸在轉角B處的運動受力簡圖

由式（11）可知，軟軸末端在圓弧內的受力的影響因素較多且關系較為復雜，與軟軸運動方向無關，受轉彎半徑和彎道包角影響較大。根據樣件結構及其尺寸參數，求得軟軸轉角B處的阻力fB為：

3.2 滑塊受力分析

滑塊是遮陽簾運動過程中的關鍵連接部件，分別裝配連接遮陽簾拉桿和遮陽簾邊條，并通過一體注塑與軟軸連接，在導軌內滑動，如圖8所示。

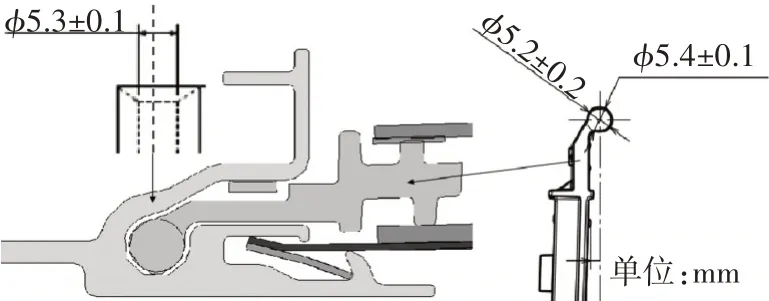
圖8 滑塊在導軌上的裝配簡圖

為避免滑塊在運行過程中產生振動異響，且考慮到生產裝配工藝，滑塊與導軌為局部過盈配合，通常其直線運行阻力fh=(5±2)N。

3.3 簾布受力分析

簾布是遮陽簾總成中的主要部件，簾布展開遮陽時分別受到Y向張緊力TY與X向張緊力TX。以下出布為例，沒卷軸桿外徑d0=20 mm，單層簾布厚度t=1.2 mm，簾布X向受力如圖9 所示，簾布收卷圈數n、卷軸展開轉角φn與簾布展開行程Sn的幾何表達式分別為：

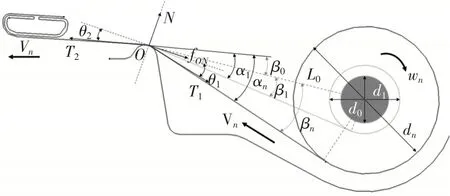
圖9 簾布在X向的受力示意

式中，d1為預卷2圈后外徑；dn為卷繞n圈時外徑。

卷軸簾布出布角αn=β0+βn，其中β0與卷軸布置相關，角度表達式為：

式中，β0為卷軸布置角，取值為19°；βn為收卷n圈后的簾布切角；L0為簾布出布點到卷軸中心的距離，取值為95 mm。

簾布運行時，切點O動態變化，以O點為原點建立直角坐標系，忽略簾布變形，得到簾布向運動方受力平衡方程為：

式中，T1為簾布出布張力；T2為簾布展開時的X向張力；θ1為坐標系下出布張力夾角；θ2為坐標系下X向張力夾角；fON為簾布受到導布橫梁的摩擦力；μ3為簾布與導布橫梁的摩擦因數；T為簾布受到導布橫梁的正壓力。

由式（18）～式（21）可得：

忽略出布角變化的影響，經計算，TX=1.11T1。

由于簾布介于兩側邊條之間，取導軌在X向的剖面，簾布的Y向張緊等效懸鏈曲線模型[9]，受力模型如圖10 所示。其中，M、N分別為邊條兩側固定點，Oy為簾布的最低點，P為圓弧MN上的任意一點，λ為Y向簾布單位長度的質量，l為簾布弧OyP的長度。以Oy為原點建立直角坐標系，靜止狀態的平衡方程為：

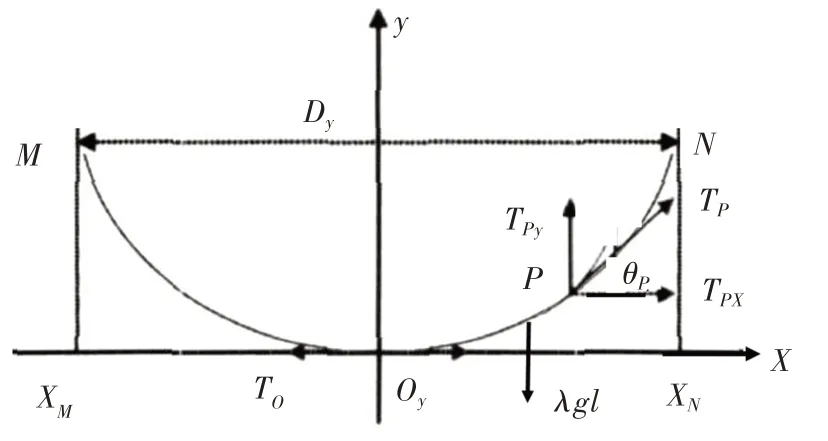
圖10 懸鏈線靜止狀態時的受力情況

式中，TP為P處簾布張力；θP為P處簾布張力的水平切角；TO為最低點Oy處水平張力。

由于遮陽簾兩側導軌水平布置，簾布最低點Oy距左側邊條固定點M的豎直高度yM與簾布最低點Oy距右側邊條固定點N的豎直高度yN相等且為該截面上簾布的最大下垂量，由式（23）～式（25）可得：

式中，L為簾布圓弧MN的長度；Dy為邊條固定點M與N的水平距離；θN為N處簾布張力的水平切角；TN為N處簾布張力。

由式（28）可知，簾布Y向張力受導軌跨距、簾布面密度以及簾布下垂量影響。為保證簾布運行平穩且運行過程中簾布整體處于張緊狀態，不能忽略簾布彈性變形，一般通過調整簾布寬幅尺寸Δl來調整Y向的預緊力。根據樣件結構及其尺寸參數，等效下垂量yN=18 mm，簾布橫向彈性系數為0.05 N/mm，得到簾布Y向張力TY為：

3.4 邊條受力分析

遮陽簾邊條在導軌處主要受到垂直運動方向的正壓力與平行運動方向的摩擦力，如圖11 所示。其中，NB為作用在邊條上的正壓力，TB為簾布對邊條的拉力，TB=TY，θB為簾布跨點處角度，αB為邊條支撐角度，FZ為導軌對邊條的正壓力，NZ為導軌對簾布的正壓力。

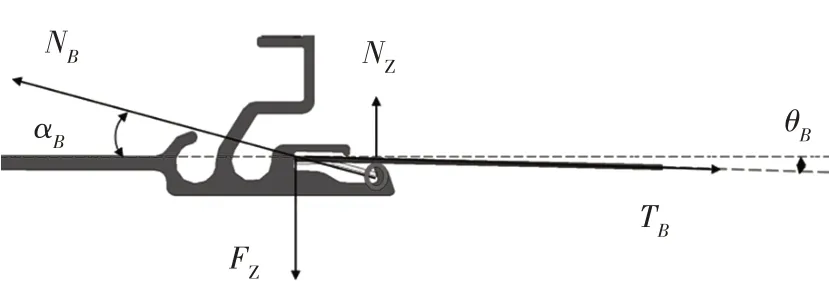
圖11 遮陽簾邊條在導軌處的受力簡圖

得到遮陽簾邊條Y方向平衡方程為：

由式（30）～式（32）可得單側邊條在導軌上的阻力fB：

式中，μB為邊條與導軌的摩擦因數；dx為簾布運行距離；S為簾布運行行程。

邊條在后梁上的受力主要作用在導向塊位置，如圖12 所示。導向塊位置與簾布出布點在Y向基本處于同一位置，由于X向受力主要作用在邊條上，摩擦因數一致時，簾布與邊條在后梁處的摩擦阻力fHL等效于簾布在導布橫梁處受到的摩擦力fON與邊條在導軌上的阻力fB之和，由式（19）～式（21）可得：

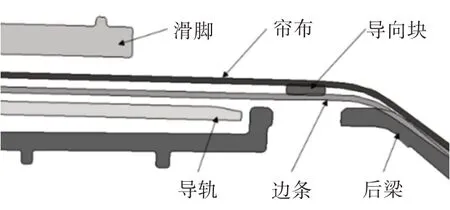
圖12 遮陽簾邊條在后梁導向塊處的受力簡圖

根據樣件結構及其尺寸參數，忽略出布角變化的影響，得到邊條在兩側導軌上的總阻力fBZ=2fB。經計算，fBZ=65.56S2×10-7，fHL=0.074n。

3.5 卷軸扭矩模型

遮陽簾回退時，簾布主要通過卷軸扭轉力回收，其結構如圖13所示，其關鍵部件為回收彈簧，為螺旋扭轉彈簧，受力如圖14所示。

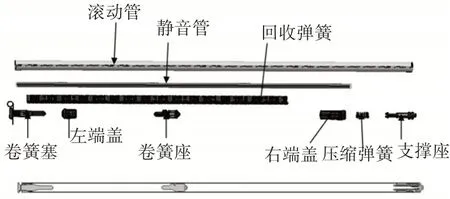
圖13 遮陽簾卷軸結構爆炸圖

圖14 卷軸內扭轉彈簧受力

扭轉彈簧按受彎矩的曲梁計算[10-11]，其扭轉角φ以及彈簧的扭轉剛度k的數學表達式分別為：

式中，d為簧絲直徑；M為扭轉彈簧彎矩；D為扭轉彈簧中徑；n1為扭轉彈簧有效圈數；E為簧絲彈性模量。

由式（13）、式（14）得：

式中，F0為卷軸初始拉力。

由式（37）可知，卷軸扭矩受彈簧絲直徑、彈簧中徑、有效卷繞圈數及扭轉角度影響。對于受動負荷彈簧，應進行疲勞強度校核[12]，以滿足遮陽簾1.0×104～1.5×104次的操作耐久要求。根據樣件結構與尺寸及卷軸彈簧扭轉剛度，求得卷軸轉動時對橫梁的摩擦阻力為：

4 遮陽簾系統阻力分析

根據本文提出的遮陽簾結構，以車前方向為正方向，嚙合點Q處為系統阻力基準點，遮陽簾打開狀態為運行起始點，以軟軸末端為運動行程參照，設R為與運行方向無關的各分阻力總和，得到遮陽簾打開與關閉時的系統阻力表達式分別為：

式中，foff為遮陽簾關閉時的系統阻力；fopen為遮陽簾打開時的系統阻力。

根據式（40）和式（41），分別對a、b、B、c、g位置進行采點計算，實測a與b的距離為600 mm，B與b、B與c的距離相等，為100 mm，c與g的距離為400 mm，同時對樣件相應位置進行阻力實測，得到遮陽簾系統運行阻力曲線，如圖15 所示，實測系統阻力與計算結果在變化趨勢上有很好的一致性。

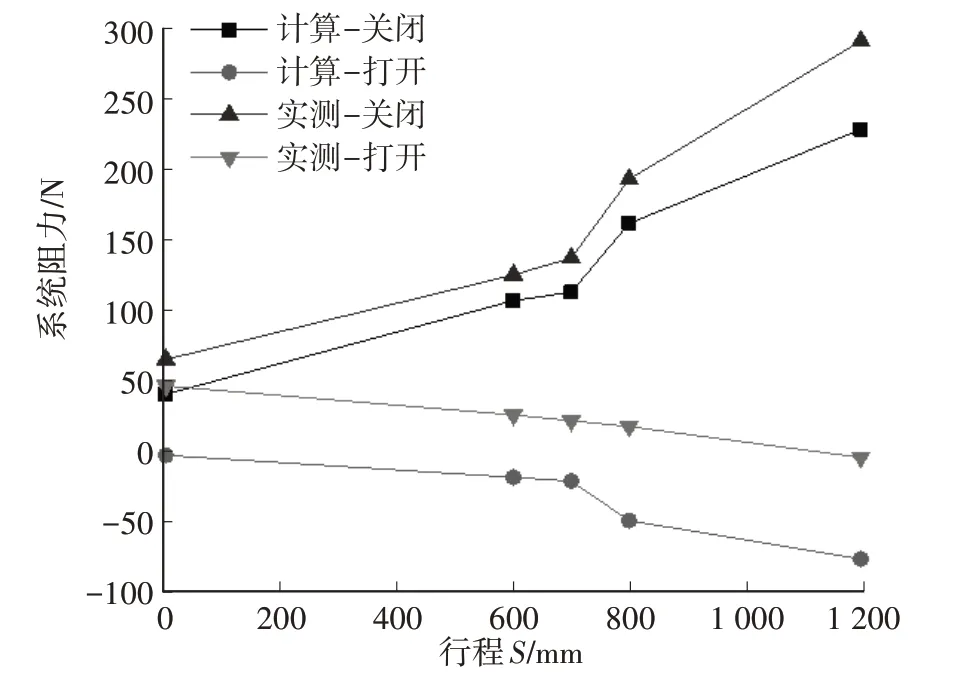
圖15 遮陽簾系統運行阻力曲線

5 結束語

本文對汽車電動遮陽簾的運行過程及其受力狀態進行了系統分析，并建立了遮陽簾的系統阻力與其開口行程的數學表達式，結果表明：遮陽簾系統阻力受力狀態復雜，影響因素繁多，主要為遮陽簾開口尺寸、軟軸曲率半徑、轉角數量與圓弧包角、簾布面密度、伸縮率及簾布下垂量、摩擦因數、卷軸初拉力/末拉力等，其中卷軸內彈簧卷收力影響最大，各運動部件之間的匹配關系及簾布屬性影響最敏感，即遮陽簾系統阻力主要由卷收方式及卷收力決定，遮陽簾系統阻力的穩定性主要由運動部件幾何關系決定。