基于APSO-SSVM的異步電動機轉子故障診斷*

郭家豪, 歐陽暉, 劉振興

(1．武漢科技大學 信息學科與工程學院,湖北 武漢 430081;2．冶金自動化與檢測技術教育部工程研究中心,湖北 武漢 430081;3．武漢第二船舶設計研究所,湖北 武漢 430064)

0 引 言

異步電動機作為現代電力傳動系統的核心部件,廣泛應用于工業、國防等領域。對異步電動機進行在線故障診斷和及時檢修電機重要元件,在提高系統穩定性和減少經濟損失方面具有重要意義[1]。在感應電機中,轉子斷條故障約占故障的5%～10%,斷裂導條上出現的過大電流會損壞其他部件造成電機停轉,進而對整個電力結構造成極大破壞甚至導致人員傷亡。因此異步電機轉子故障診斷方法的研究一直是故障診斷領域的熱點[2]。

電機電流信號特征分析(MCSA)作為診斷電機故障的標準方法,通過對定子電流頻譜中表現為(1±2ks)(s為異步電機的轉差率;f為電源的頻率;k=1,2,…)的頻率成分進行檢測來確定斷條故障特征[3]。故障特征頻率取決于電機的轉差率,其會隨著電機負載的波動而發生變化從而造成故障特征頻譜振蕩,故障特征受到主頻淹沒變得難以檢測。為了消除噪聲及主頻的影響,文獻[4]通過經驗模態分解(EMD)對定子電流提取模態分量并重構,經希爾伯特變換(HHT)解調,實現故障頻率的準確分辨。文獻[5]通過小波變換,將定子電流信號分解為近似系數和細節系數,通過對細節系數的分析發現平均偏差與故障程度成正比,實現故障檢測并劃分故障嚴重程度。文獻[6]將定子電流信號直接輸入到卷積神經網絡中,構建了一種端對端的故障學習模型,達到對故障特征的準確分類。然而,這些診斷方法在應用中都存在一些缺陷:EMD算法在信號分解和濾波中存在著模態混疊現象,導致不同的時間特征成分存在于一個本征模態分量中,使得HHT的模態選擇和頻譜分析變的困難;小波變換和分解的效果很大程度上取決于小波母函數的選擇,以及分解層數的確定,這種選擇取決于實際的應用場景;卷積神經網絡的端對端故障診斷模型的網絡結構參數確定困難,模型訓練依賴于龐大的數據驅動。

支持向量機(SVM)作為解決分類問題的有力工具,其通過在高維或無限維空間中構造一個或多個超平面,來劃分數據樣本。為了發揮SVM小樣本數據分類精度高、診斷速度快的優點,并且克服SVM數據特征選取困難和超參數難以確定的缺點,本文將SVM分類模型和自適應粒子群優化(APSO)算法相結合,提出了一種適用于異步電機斷條故障診斷的自適應粒子群優化逐序支持向量機(APSO-SSVM)的診斷方法。核心思路是:利用經驗小波變換(EWT)的自適應低通濾波性能濾除定子穩態電流中的各種噪聲和高次諧波,將故障分析限定于反映故障特征的單分量信號;然后通過對穩態電流信號進行周期截斷,得到訓練集和測試集的樣本和標簽,并在時域對樣本進行特征提取,通過特征重要性排序,篩選出影響模型分類結果中占權重大的特征;最后將特征提取后的信號樣本導入SSVM模型進行訓練,使用APSO算法確定最佳超參數,得到轉子斷條故障分類模型。相比于現有方法[4-6],本文所提方法用EWT進行濾波處理無需設置參數,能有效抑制模態混疊,自動進行時頻分解。同時APSO-SSVM分類模型不需要依賴于大量的數據樣本,篩選后的特征清晰,超參數自適應確定,模型分類精度高。

1 問題和算法描述

1.1 電機穩態下的轉子斷條故障特征

假設異步電機由理想的三相電源供電,a、b、c三相電流ia(t)、ib(t)、ic(t)表達式為

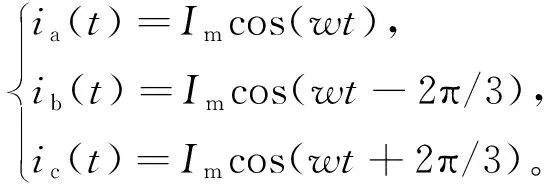
(1)

式中:Im為電路基波分量的最大值;ω為基波角頻率,ω=2πf。

當電機發生斷條故障時,定轉子之間的氣隙磁場會發生畸變,原本穩定的正弦定子電流信號就會感應出一系列故障諧波分量(1±2ks)f,k=1,2,3…。(1±2ks)f為分布在基頻周圍的故障邊頻量。此時,定子三相電流iaf(t)、ibf(t)、icf(t)仍然對稱,分別是由其故障諧波所調制而成的多頻率信號。在故障診斷中常取k=1時的左右邊頻帶諧波頻率(1±2s)f來識別斷條故障,當只考慮電源頻率f和(1±2s)f的頻率分量時,定子電流斷條故障的數學模型為[7]

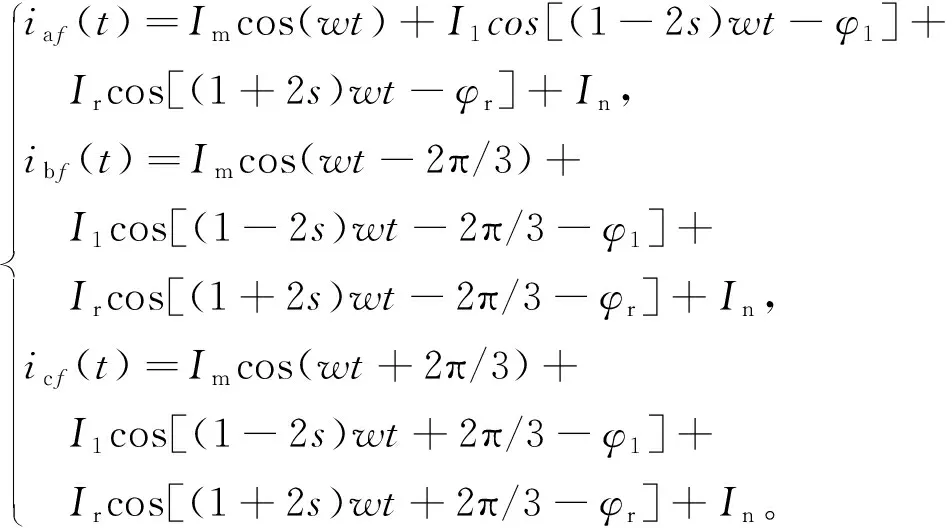
(2)

1.2 APSO算法原理

PSO算法是一種基于種群優化的進化算法,在尋找最優解的過程中,每個粒子都存在個體行為和群體行為[8]。在算法迭代過程中,每個粒子沿著其最優解和群體中全局最優位置的方向移動。每個粒子計算自己的速度并在每次迭代中更新位置。假設pi,j代表第i個粒子所遇到過的自身最佳位置,pg,j代表當前所有粒子中所挑選出的全局最佳位置,t代表迭代的次數。則第i個粒子在第j維空間中的第t次迭代的運動速度可以表示為[9]

vi,j(t)=w×vi,j(t-1)+c1r1×

[pi,j-xi,j(t-1)]+c2r2×[pg,j-xi,j(t-1)]

(3)

式中:w為粒子飛行速度中的慣性權重;c1、c2分別為(0,2)區間取值的個體和社會學習因數;r1、r2分別為兩個相互獨立的取值范圍在[0,1]的隨機數。

粒子的位置更新由以下式子表示:

xi,j(t+1)=xi,j(t)+vi,j(t+1)

(4)

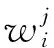
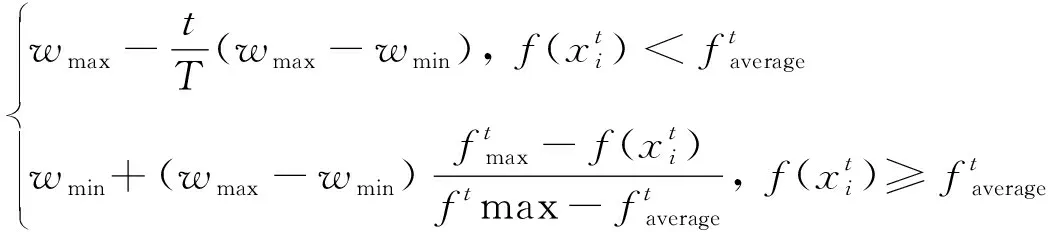
(5)

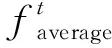
適應度越大,說明距離最優解越近,此時更需要局部搜索;適應度越小,說明距離最優解越遠,此時更需要全局搜索。與基本粒子群算法相比,現在粒子的慣性權重是動態更新的,且與迭代次數和每個粒子的適應度都有關。

1.3 SSVM分類模型

SVM的基本原理簡要介紹如下,給定樣本和標簽對的訓練集(xi,yi),i=1,2,…m,其中xi∈Rn,且yi∈{+1,-1},考慮由(w,b)定義的超平面,w是權重向量,b是偏置,可用以下函數對x進行分類[11]。

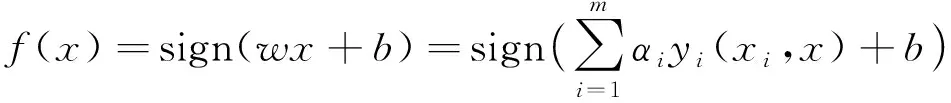
(6)

在實踐中,數據通常不是線性可分的。然而,仍然可以通過將數據點通過非線性映射變換到另一個更高維空間(特征空間)來實現線性模型,使得數據點線性可分。該映射由核函數K完成。

SVM的非線性決策函數由以下函數給出:

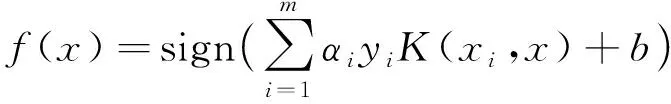
(7)

式中:Ki(xi,x)為核函數,常用的是高斯徑向基核函數(RBF),其分類效果好,具有平滑性和局部性的特點,可以有效地避免過擬合和欠擬合的問題[12]。

RBF的超參數γ和懲罰因子C都影響著分類精度。圖1展示了在二分類問題中采用RBF時不同的γ和C對超平面的形成以及分類準確性的影響。

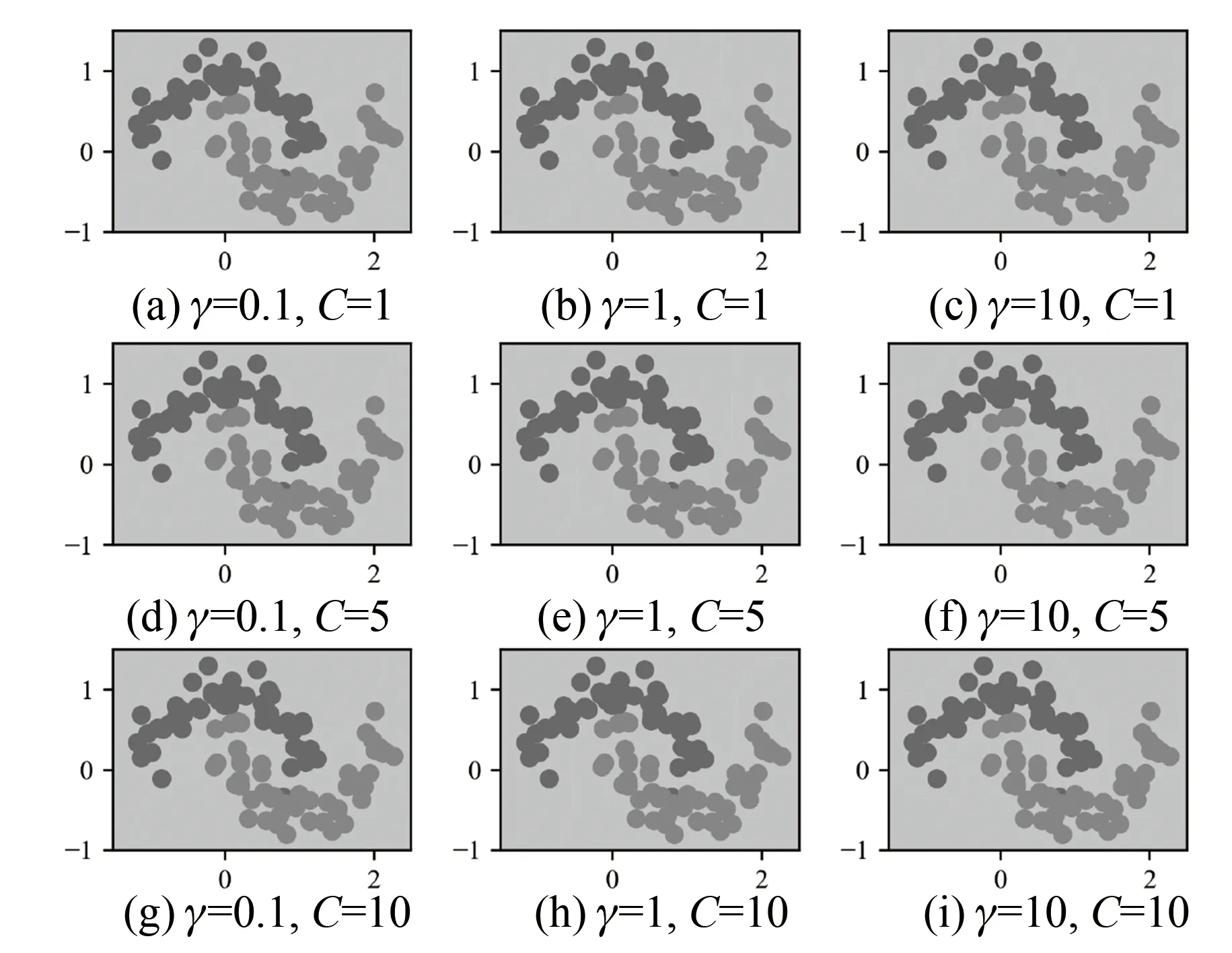
圖1 不同超參數對SVM分類的影響

由圖1可以看出,γ越大,高斯圖形越窄,模型復雜度越高,容易導致過擬合;γ越小,高斯圖形越寬,模型復雜度越低,容易導致欠擬合[13]。

在SVM分類模型中,要使決策邊界能夠忍受小部分誤差,從而提升泛化能力,因此懲罰系數C是用來懲罰SVM對最大邊際的追求,從而在正確分類和最大化邊際兩個目標中找到一個最佳平衡點。

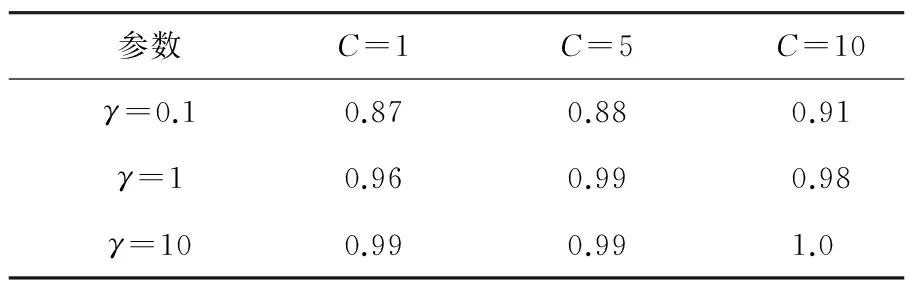
表1 不同超參數下的SVM分類精度

由以上分析可知,要使模型能夠達到最佳的分類精度,故障檢測能夠更準確,SVM參數的選擇是很重要的。而基于APSO優化的SVM分類模型,可以自主確定使模型表現效果最佳的γ參數和懲罰因子C,實現斷條故障的精確診斷。

SSVM模型是在SVM的基礎上提出的逐序分類模型,其思路是對于多分類問題,將其依次拆解為多個二分類問題,在每次二分類的SVM模型中,均使用APSO算法來尋找最佳超參數,依次來增強模型的泛化能力、提高分類精度。其流程圖如圖2所示。

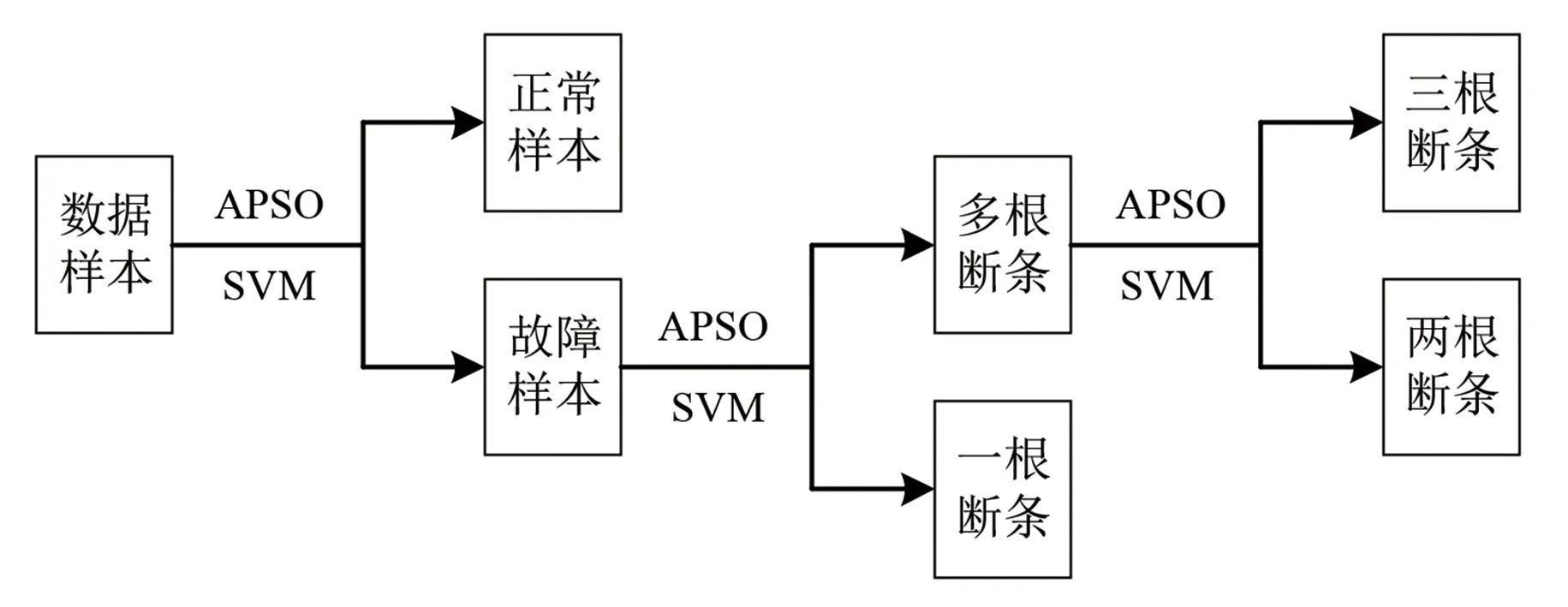
圖2 SSVM分類模型流程圖

2 基于APSO-SSVM的轉子斷條故障診斷方法

故障診斷流程主要包括數據采集、數據濾波、特征提取和故障分類四個部分,原理框圖如圖3所示。為證明本文所提方法的魯棒性和泛化性,先對電機進行有限元建模分析,獲取不同負載下的斷條故障數據,再用APSO-SSVM方法對故障進行分類。

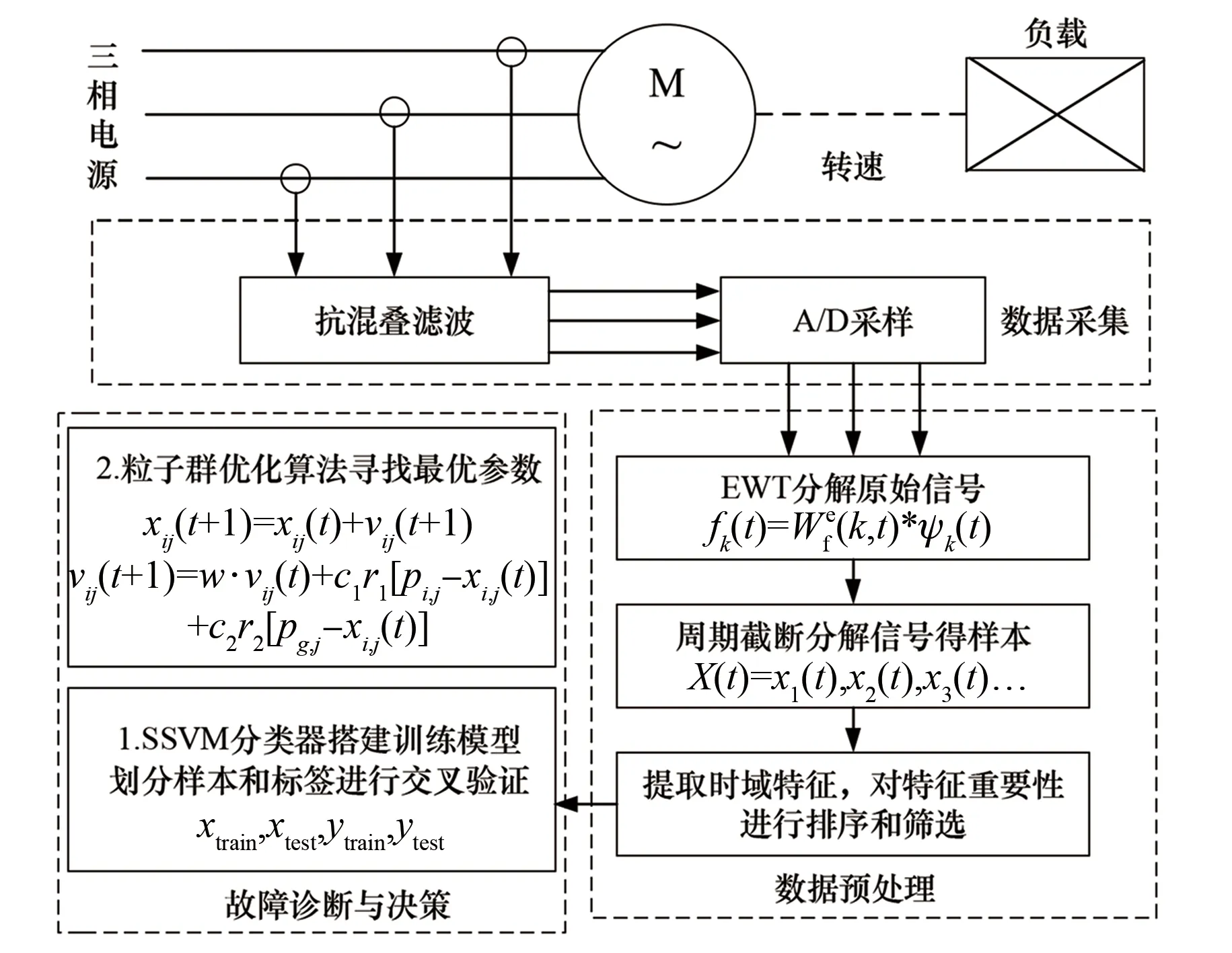
圖3 故障診斷原理框圖

數據預處理采用EWT算法對原始信號進行濾波降噪,并對濾波之后的信號進行周期截取獲得樣本,最后對每一類樣本點進行特征提取和特征篩選。特征提取的作用主要是降低信號的維度,提取能夠代表原信號特征的時域量,通過隨機森林算法篩選出最能決定分類精度的優良特征量。最后通過搭建試驗平臺對所提方法進行驗證。

2.1 基于ANSYS的電機有限元仿真

本文采用ANSYS中的Maxwell 2D仿真,構建了鼠籠式異步電機的有限元模型,其具體步驟如下:

(1) 在RMxprt中設置電機基本參數

Maxwell提供構建鼠籠異步電機2D有限元模型的工具,首選的方法是利用RMxprt異步電機模型進行自動轉換。相關電機參數見表2。

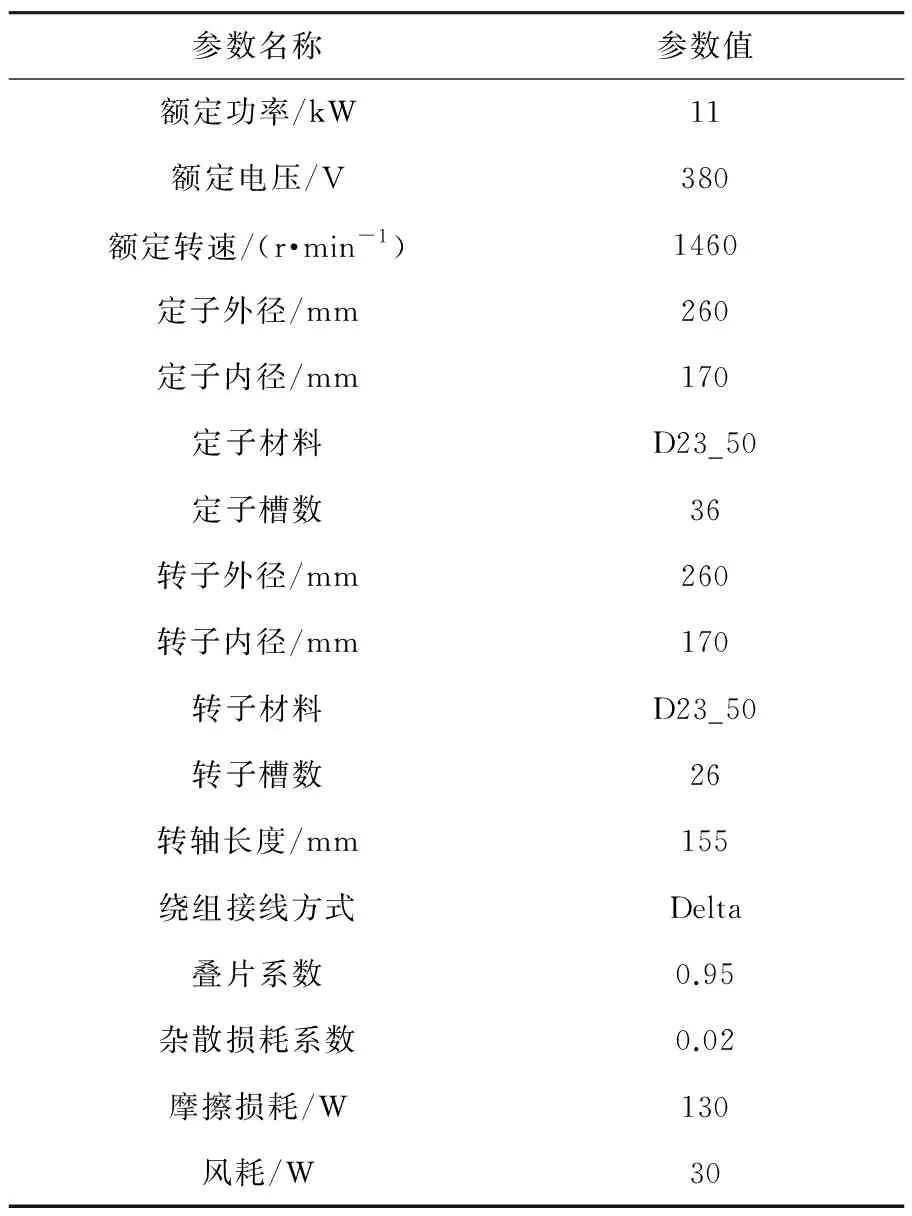
表2 電機各項參數

(2) 在Maxwell 2D中設置轉子斷條故障

當鼠籠式異步電機遭遇轉子導條斷裂時,可以將斷裂位置視為電路的開路。在未發生故障的正常情況下,轉子導條材料的電導率通常為2.3×107s/m。為了精確地模擬轉子斷條的故障情況,設定斷條的電導率為20 s/m,這等效于在斷條處引入了極大的電阻。圖4為已標注故障斷條位置的電機的Maxwell 2D模型。仿真設置了四種運行狀態,分別為正常狀態以及具有1根、2根和3根斷條的故障狀態。

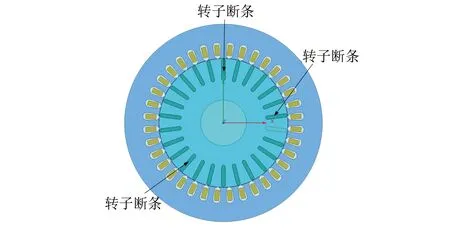
圖4 電機Maxwell 2D模型

(3) 設置運行條件

將電機在上述四種故障狀態下運行,運行的載荷條件分為三種,分別是輕載40 N·m(轉速1 480 r/min),額定負載72 N·m(轉速1 460 r/min),重載106 N·m(轉速1 440 r/min),其中額定負載下對應的1根斷條的時域波形圖如圖5所示。

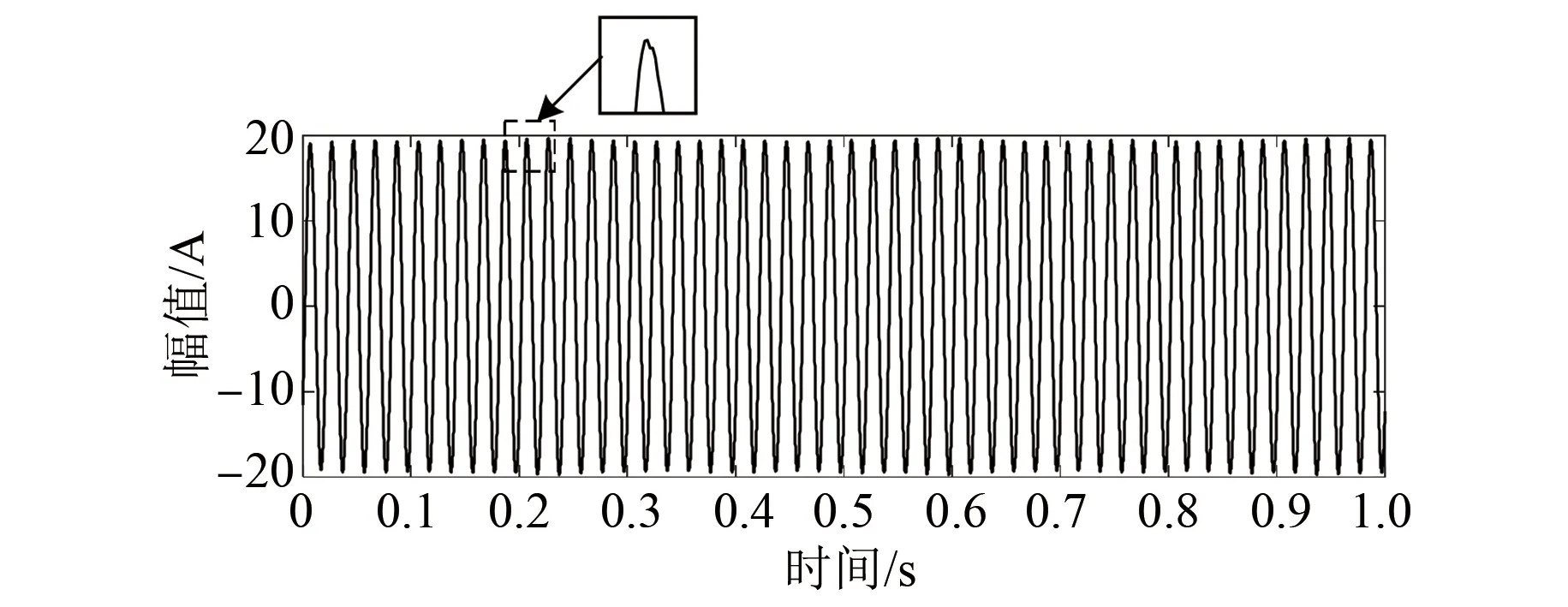
圖5 定子A相電流時域波形圖

在ANSYS有限元仿真下,不同負載和故障下電機穩態運行的時間均為1 s,采樣頻率為10 kHz。以上分析均以額定負載條件下,一根斷條故障的定子A相電流為例。

2.2 基于EWT的信號分解

EWT的分解思路是通過對信號的頻譜進行分段劃分,構建合適的小波濾波器組,對信號進行分解。經驗小波是定義在區間Λn上的帶通濾波器組,利用范數不等式和Meyer小波的思想進行設計。傅里葉變換的整個支撐區間可由Λn劃分為[14]

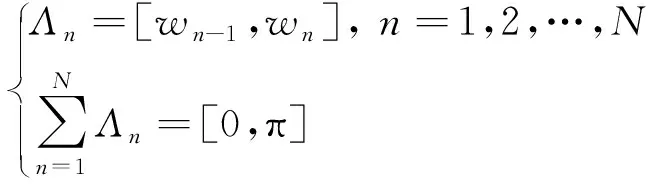
(8)

根據上述濾波器的構造方法,只考慮[0,π]的支撐區間,可建立第一個區間為尺度函數確定的濾波器,其他區間為經驗小波函數確定的濾波器組,并以此為基礎進行EWT。借鑒經典小波變換的思路,細節系數為[15]

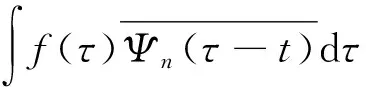
(9)

式中:Ψn(ω)為經驗小波函數;φn(ω)為經驗尺度函數。

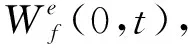
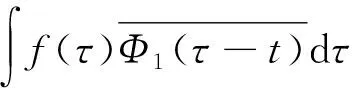
(10)

式中:Ψn(ω)和Φn(ω)分別為Ψn(t)和φn(t)的傅里葉變換。

傅里葉逆變換記為F[·]和F-1[·],由此信號f(t)的重構表達式為[16]

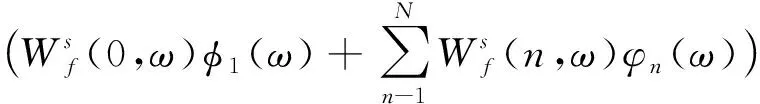
(11)

EWT通過設計合適的小波濾波器庫提取信號的不同模式,信號f(t)分解得到的頻率由低到高的調幅-調頻單分量成分為fk(t)(k=1,2,3…),則:

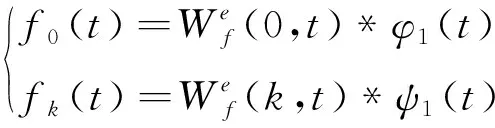
(12)

EWT分解會減少產生任何形式的無效分量,對于給定的信號x(t)其表達式如式(13)所示:

x(t)=y(t)+n(t)

(13)

式中:y(t)為頻率50 Hz時的低頻正弦信號;n(t)為高頻噪聲信號;x(t)為兩者信號的時域疊加。

信號分解的目的在于將不同頻率段的信號分離以便于提取所需要的部分,原始故障信號經過EWT分解結果如圖6所示。

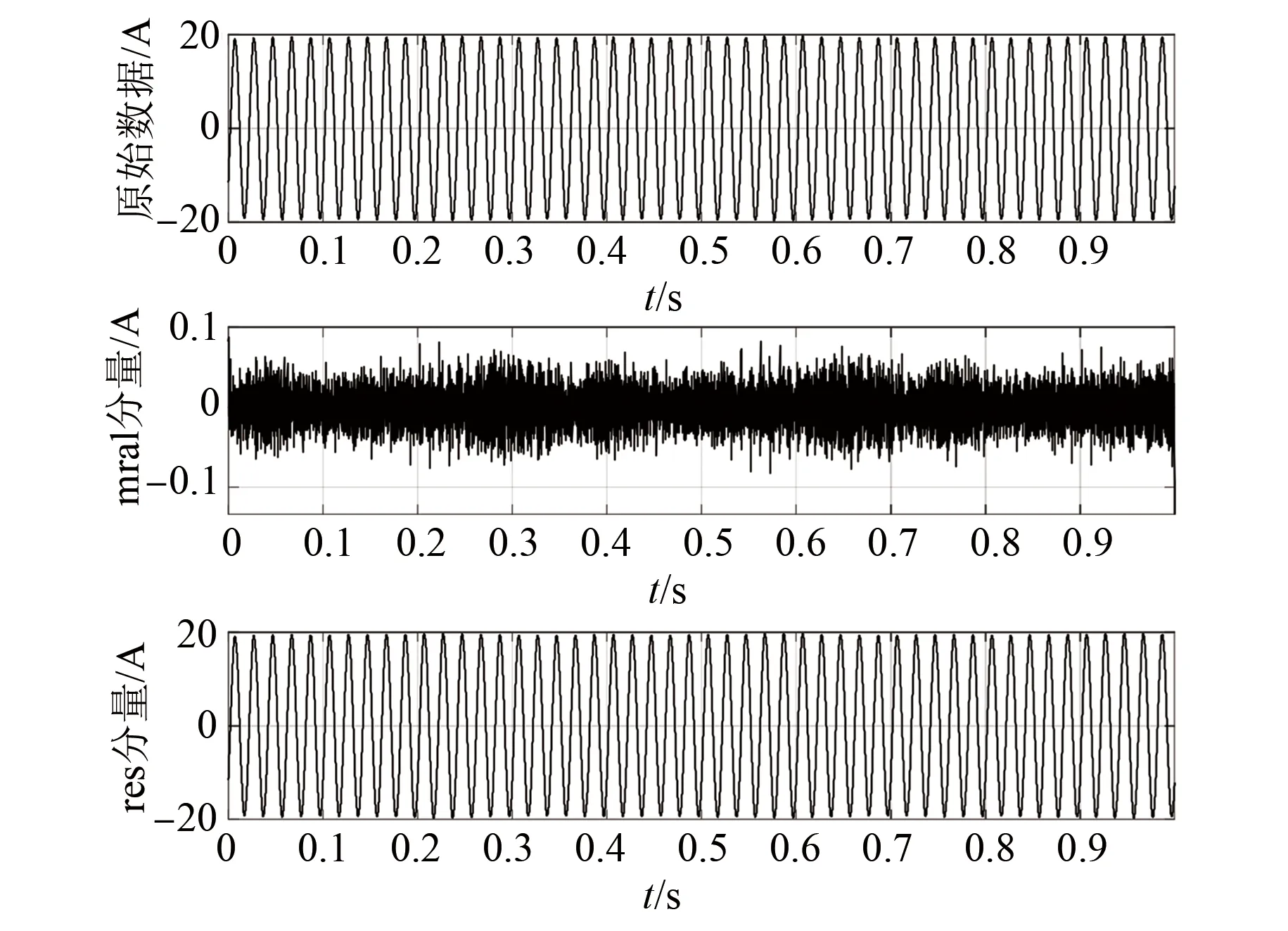
圖6 EWT分解信號

圖6中,mra1分量是原始信號中所帶的噪聲部分,res分量是經去除高次諧波后的穩定信號,可以看出去噪后的信號沒有發生模態混疊。

對分解后的信號進一步做頻譜分析如圖7所示,發現高頻噪聲均被分離,且EWT沒有損失主頻附近的故障頻率,保留了故障特征。

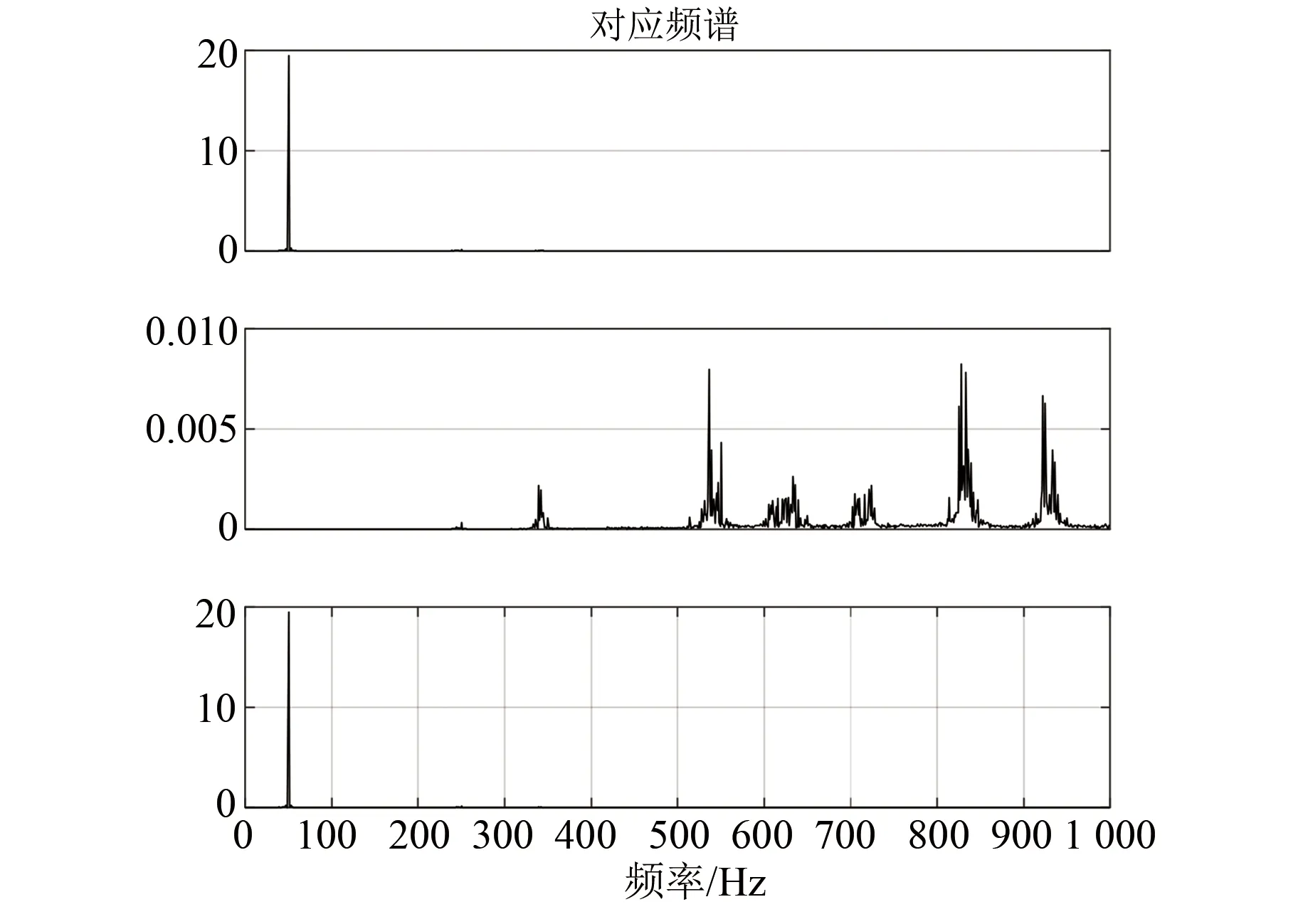
圖7 EWT分解信號的頻譜圖

2.3 時域特征提取與分析

在使用SVM分類器進行分類之前,需要再對數據進行劃分。如圖8所示對定子電流信號進行周期截斷,以每200個信號點為一個周期,一個周期的數據即為一個樣本點,周期截取之間無間隔。

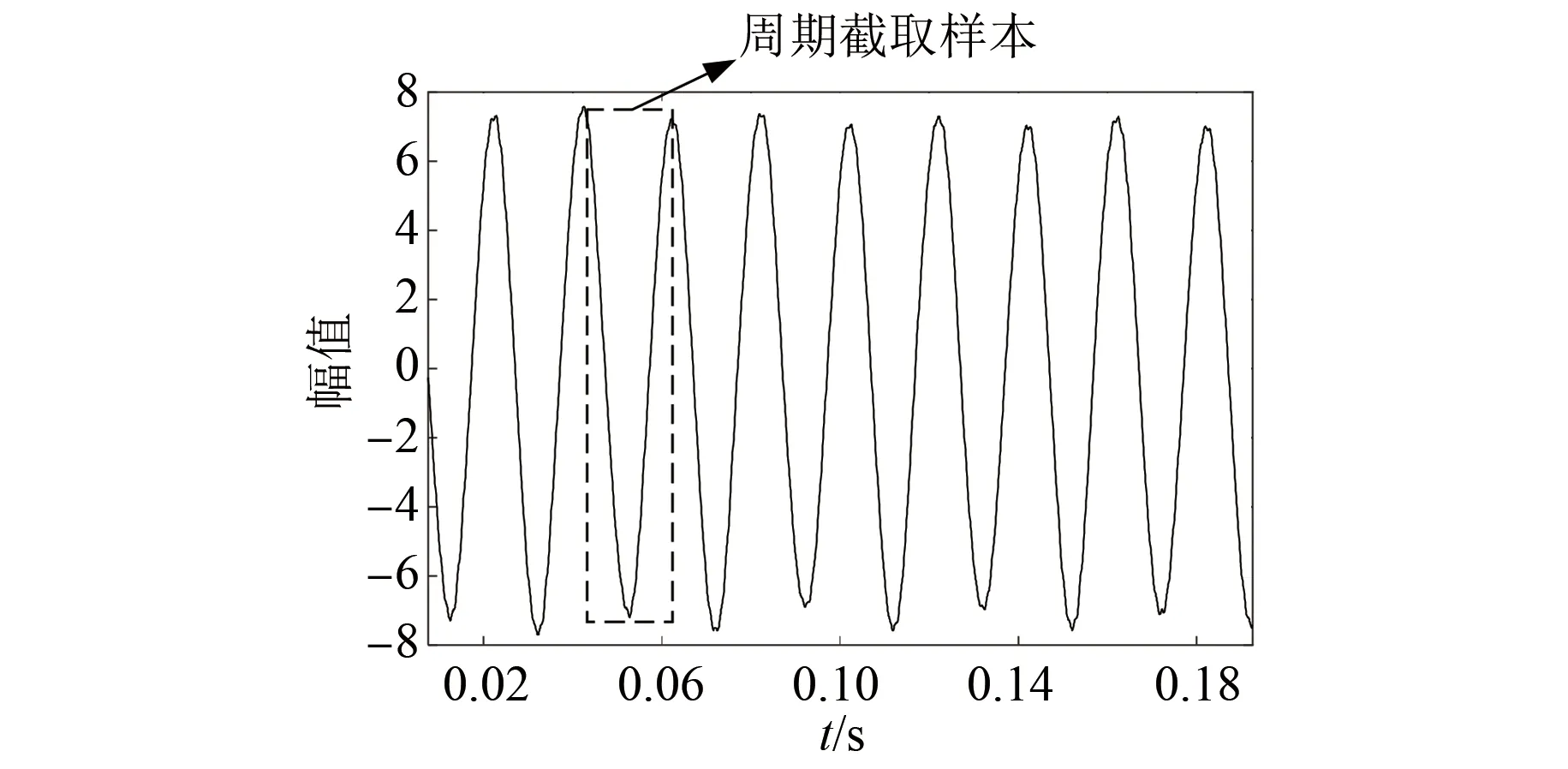
圖8 時域信號的周期截取

輸入每一個周期樣本記為xi,i=1,2,…,m,其中m為樣本總數。每一類別的樣本標簽記為yi,k為分類的類別數。對樣本進行時域特征量提取,提取10個時域特征,分別是單個樣本的最大值(max),最小值(min),平均值(me),峰峰值(pk),整流平均值(av),方差(va),標準差(st),偏度(sk),均方根(rm)和峰值因子(C)。使用隨機森林策略對樣本重要性進行比較,結果如圖9所示。

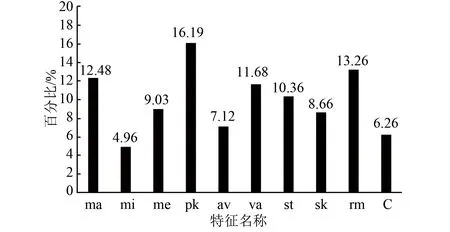
圖9 特征重要性直方圖

由圖9可以篩選出占比相對較高的特征,考慮SVM分類的準確性,并不是特征維度越高越好,因此本文選擇前六個特征輸入到SVM模型中。

2.4 APSO優化SSVM

APSO算法的目的就是為了找到SVM中的兩個最優超參數懲罰系數C和高斯徑向基的自帶參數γ,從而使模型的分類精度達到最高。在劃分正常樣本和故障樣本的SVM模型中粒子的探尋軌跡如圖10所示。

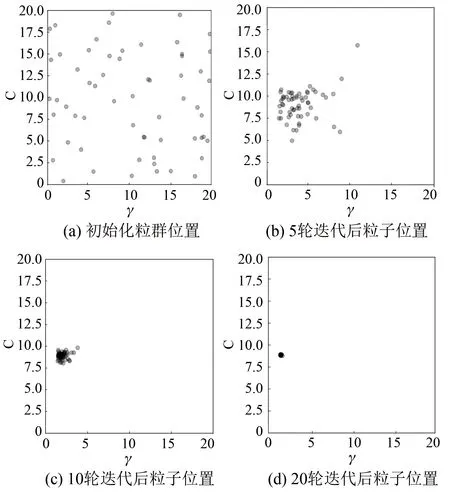
圖10 粒子群迭代位置變化

在進行算法迭代中,初始粒子群數目為60,粒子群迭代二十輪,初始速度和位置均為隨機初始化。

在訓練過程中通過觀察粒子的適應度變化來判斷模型的收斂速度,適應度f(x)在故障診斷模型中定義為模型分類的準確率,其由式(14)所示:

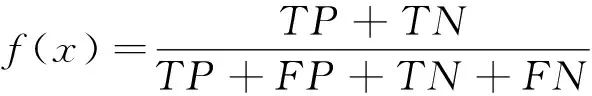
(14)

式中:TP為被正確預測的正例個數;TN為被正確預測的反例個數;FP為被錯誤預測的正例個數;FN為被錯誤預測的反例個數。

迭代過程中的粒子平均適應度隨迭代次數的變化如圖11所示。由圖11可知,在初始粒子數目和迭代次數相同的情況下APSO在迭代在第6輪之后粒子就已經找到了全局最優值點,而PSO在迭代17輪之后才能找到最佳模型參數。可見,APSO的收斂速度更快,不易陷入局部最小值,穩定性更好。

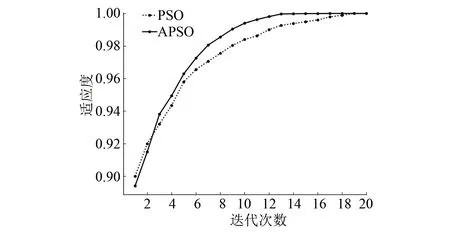
圖11 粒子群迭代適應度變化

對ANSYS仿真下,電機的不同負載條件下的故障特征進行上述診斷步驟進行故障樣本和正常樣本的第一輪分類,其相對應的分類精度和算法平均迭代次數如表3所示。

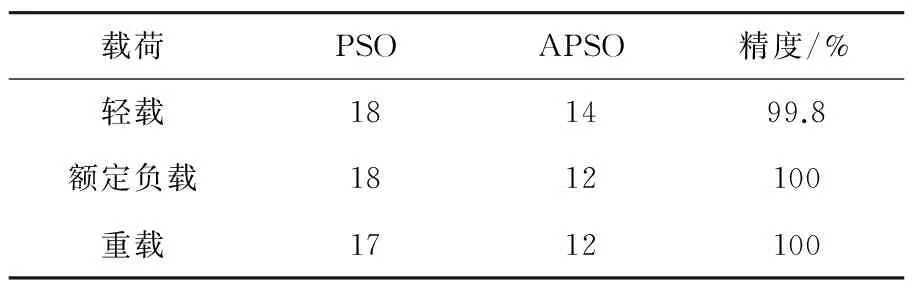
表3 分類精度和迭代次數

由表3可知,基于APSO-SVM的算法,收斂速度更快,并且尋找的最優參數使得SVM分類器在不同負載條件下,均能實現斷條故障的準確分類。

3 試驗結果分析

3.1 試驗裝置

試驗系統主要由電源、試驗電機和數據采集器等組成,如圖12所示。試驗過程為在正常狀態下對電機進行穩態信號采樣,再將電機的轉子分別打斷為1根、2根和3根,并依次收集斷條定子電流數據。電機的型號和銘牌參數如表4所示。數據采集板由調理電路和DSP數據采集卡構成。試驗過程中,采樣頻率為10 kHz,采樣時間為1 s。

表4 試驗電機參數

圖12 電機試驗臺

3.2 試驗結果分析

根據2所述的診斷步驟,對EWT降噪分解后的樣本進行周期截斷,共計200個樣本數據。其中,故障類型分為4類,分別是正常狀態、1根斷條、2根斷條和3根斷條。每種故障類型樣本數為50,按7…3的比例進行訓練集和測試集劃分,然后導入APSO-SSVM分類模型中進行訓練,得到驗證結果的混淆矩陣如圖13所示。

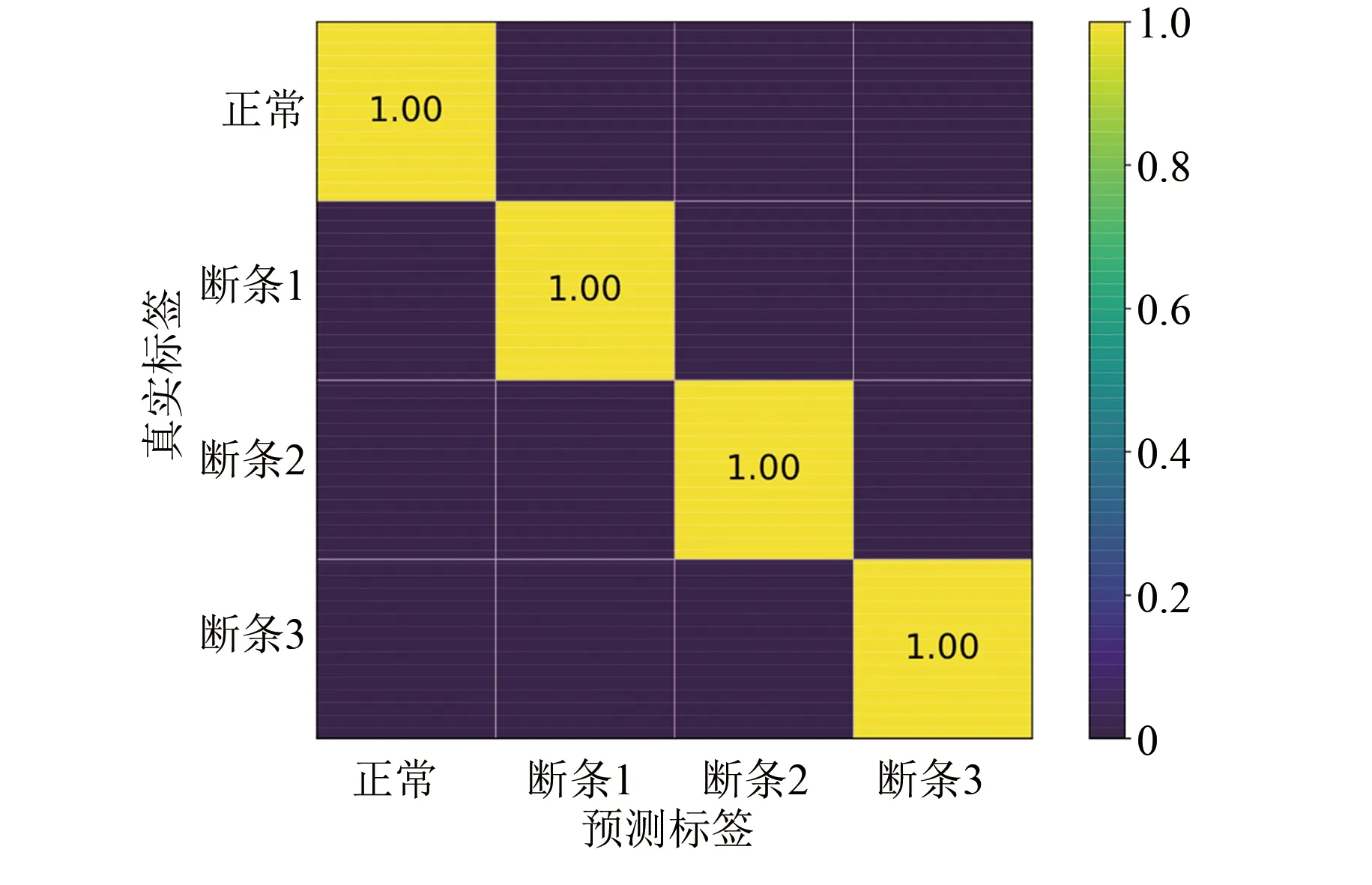
圖13 預測結果的混淆矩陣

相比于其他的SVM智能優化算法,本文做了相應的消融試驗進行對比,來進一步驗證所提APSO-SSVM模型分類的精確性,結果如表5所示。表5中的APSO-SSVM為四輪逐次分類的平均迭代次數。

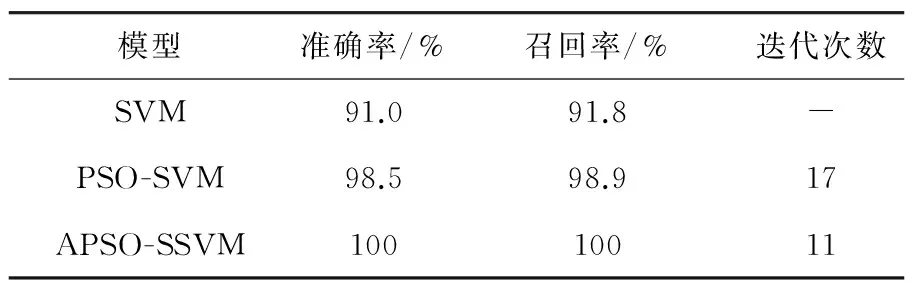
表5 各模型分類效果對比

由表5的分類結果可知,APSO-SVM算法的分類精度最高達到100%,而且迭代速度相比PSO算法更快,說明了EWT濾波后的信號提取時域特征的有效性,以及APSO-SSVM故障診斷模型對實際電機斷條故障分辨的準確性和實用性。

4 結 語

基于傳統頻譜分析的MCSA電機故障診斷,無法檢測出轉子的斷條數目和故障類型,而且原始的信號往往摻雜大量的噪聲和高次諧波干擾,這對于不同種類的故障識別是不利的。EWT可以自適應的濾除高次諧波和噪音,得到平穩的定子電流信號。通過對樣本信號進行時域特征提取以及特征重要性篩選,可以找出影響故障分類的決定性因素,并且避免了頻譜分析中高次諧波和邊頻帶的干擾。將提取到的時域特征用于小樣本數據驅動的SSVM分類模型,并采用改進的APSO算法來優化SSVM的超參數,加快了參數尋優的迭代過程,最終實現對轉子斷條數量的高精度診斷。模型提取出的特征對于定子電流信號的故障診斷具有普適意義,為進一步研究信號的故障診斷方法提供了重要的參考。