2023年新高考Ⅰ卷第22題解法探究
2023-10-26 11:03:54葉誠理林品玲
數理化解題研究 2023年28期
葉誠理 林品玲
(福建省福清第一中學,福建 福清 350300)
解析幾何一直就是高考試卷的主干知識,2023年新高考Ⅰ卷就把解析幾何中的拋物線作為壓軸題考查,給人耳目一新的感覺.
1 試題呈現

(1)求W的方程;

本題以拋物線中的內接直角三角形為載體,考查了拋物線的方程、性質和弦長計算,考查數形結合、化歸轉化、函數方程等思想,考查數學抽象、邏輯推理、直觀想象、數學運算等核心素養,體現基礎性、綜合性和創新性.
本題的命題背景源于教材(新人教A版選擇性必修一P46頁章末第10題)、往年數學競賽(上海1998年高中數學競賽試題第12題)和高考題(2017年高考數學新課標Ⅰ卷理科第10題).
2 解法探析
2.1 第(1)問解析

2.2 第(2)問解析



圖1 解法1示意圖

x2-kx+ka-a2=0.
則xA·xB=a·xA=ka-a2.即xA=k-a.



令k2=m,則m∈(0,1].
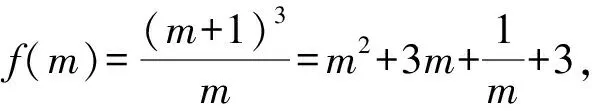



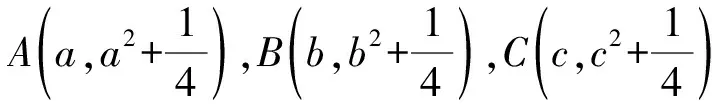






圖2 解法3示意圖







圖3 解法4示意圖
2.3 試題推廣
事實上,對于一般的拋物線W:x2=2py(p>0),已知矩形ABCD有三個頂點在W上,則有

推論2若四邊形ABCD為正方形,則面積的最小值為2p2;

3 策略剖析
上述幾種解法的解題過程充分體現了依托幾何直觀,合理運算求解的解題策略.以解法1為例,見表1.

表1 策略剖析表
另外,掌握代數運算的技巧也是必不可少的,凸顯解析幾何的本質:用代數的方法來研究幾何問題. 體現在如下幾點:

因此,要想順利解決本題,需要學生掌握扎實的數學基礎知識,學會在復雜情境中懂得靈活地、綜合地運用所學知識分析問題、解決問題的能力,即充分挖掘幾何特征,實現巧妙轉化和創造性地求解,問題的解決過程充分考查了學生的直觀想象、抽象概括、邏輯推理、數學運算核心素養和良好的心理素質,體現了命題者的意圖.
猜你喜歡
語數外學習·高中版上旬(2024年18期)2024-02-20 00:00:00
中學生數理化·中考版(2021年10期)2021-11-22 07:26:38
數學小靈通(1-2年級)(2020年9期)2020-10-27 03:24:18
當代貴州(2019年41期)2019-12-13 09:28:56
中學生數理化·中考版(2017年10期)2017-04-23 06:29:38
中學生數理化(高中版.高二數學)(2017年1期)2017-04-16 05:33:44
新民周刊(2016年15期)2016-04-19 18:12:04
新民周刊(2016年15期)2016-04-19 15:47:52
中國共青團(2015年7期)2015-12-17 01:24:38
漫畫月刊·炫版(2014年3期)2014-05-27 04:17:21

