淺談四點共圓的簡單應用
胡繼春
《義務教育數學課程標準》(2022版)指出:幾何的學習要從演繹證明、運動變化、量化分析三個方面研究這些圖形的基本性質和相互關系。這樣的學習過程,有助于學生在空間觀念的基礎上進一步建立幾何直觀,提升抽象能力和推理能力。
不少地方的教材已經不學習四點共圓了,或者把四點共圓放在閱讀材料中,但是如果我們學會四點共圓,如果選擇、填空題里有幾何難題,那不管我們用什么方法,把答案做對就沒問題。考場上的書寫表達,有一種“改頭換面”的方法——將用了四點共圓的書寫方法,改寫成沒用四點共圓的書寫方法。
一、 引例
在剛剛結束的2023年中考,安徽省中考試卷中第22題是一道幾何綜合性的解答題,不少學生表示題目難度比較大,尤其是第二問無從下手。現在我們一起來研究這道題。
【引例】(2023年安徽第22題)在Rt△ABC中,M是斜邊AB的中點,將線段MA繞點M旋轉至MD位置,點D在直線AB外,連接AD,BD。
(1)如圖1,求∠ADB的大小;

圖1
(2)已知點D和邊AC上的點E滿足ME⊥AD,DE∥AB。
(ⅰ)如圖2,連接CD,求證:BD=CD;

圖2
本題我們只研究第(1)問和第(2)問的第(ⅰ)問,第(2)問的第(ⅱ)問不研究。
分析:(1)根據旋轉的性質得出MA=MD=MB,根據等邊對等角得出∠MAD=∠MDA,∠MBD=∠MDB,在△ABD中,根據三角形內角和定理即得出∠MAD+∠MDA+∠MBD+∠MDB=180°,進而即可求解;
我們先來看中考參考答案怎么解答的。

(2)(ⅰ)延長AC,BD交于點F,證明四邊形AMDE是菱形,進而根據平行線分線段成比例得出,AF=AB,根據等腰三角形的性質,得出D是BF的中點,根據直角三角形斜邊上的中線等于斜邊的一半,即可得證;
方法一:證明:如圖3,延長BD、AC,交于點F,則∠BCF=90°,
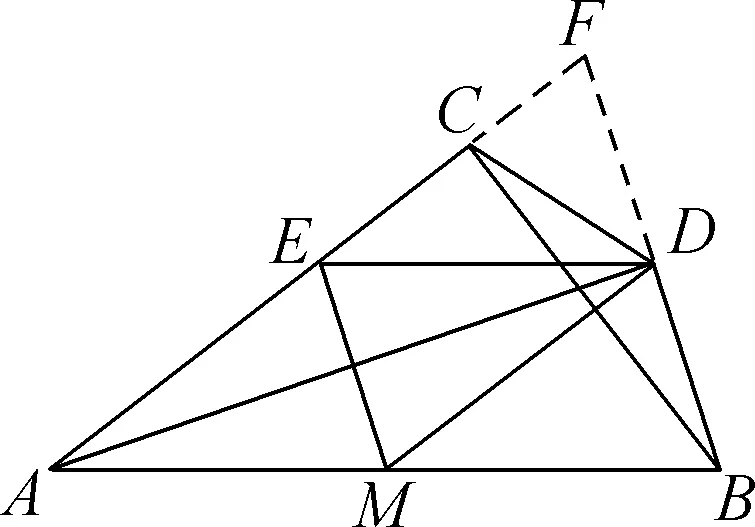
圖3
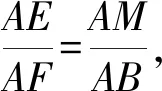
方法二:因為ME⊥AD,∠ADB=90°,所以EM∥BD,又因為DE∥AB,所以四邊形BDEM是平行四邊形。所以DE=BM。所以AM=BM=DE。所以DE∥AM且DE=AM,所以四邊形AMDE是平行四邊形。因為ME⊥AD,所以平行四邊形AMDE是菱形。所以∠CAD=∠BAD,又因為∠ACB=∠ADB=90°,所以A、C、D、B四點共圓,因為∠CAD=∠BAD,所以BD=CD。
本題考查了三角形內角和定理、菱形的性質與判定、平行線分線段成比例、相似三角形的性質與判定、直角三角形斜邊上的中線等于斜邊的一半、勾股定理等,熟練掌握相似三角形的性質與判定是解題的關鍵。第(2)問的第(ⅰ)小問輔助線的作法復雜且在考場比較緊張的狀態下難以想到。比較一下這兩種證明方法,如果沒有四點共圓,就是考查了學生對相似的理解,通過相似轉化得到所需要的結論,但當我們學習了四點共圓后很快就能夠得出結論,省去了添加輔助線和相似。這種思考比相似比例的轉化簡單許多,這樣作比較,就能突出四點共圓的優勢了。
著名的數學家斯托里亞爾說:“數學教學是數學語言的教學。”數學具有一定的抽象性,文字語言和符號語言轉換頻繁。
以往的論文中都是研究四點共圓的證明方法和四點共圓的應用,文章通過探討用四點共圓和不用四點共圓等不同方法解決問題,體現出四點共圓解題的優越性。
二、 常用的四點共圓的判定方法
1.如果四個點到一個點的距離相等,那么這四個點在同一圓上
這個判定方法是根據圓上的點可以看成是到定點的距離等于定長的點的集合這個定理得出的,也是最基本判定方法,其他的判定定理的直接證明法也都是根據它得出的。
2.如果四邊形的一組對角互補,那么這個四邊形的四個點共圓
3.如果兩個點在一條線段的同旁,且和這條線段的兩個端點連線所夾的角相等,那么這兩個點和這條線段的兩個端點四點共圓
方法2和3是幾何題中最常用的判定方法,此外還有如兩條線段相交各自被交點分成的兩條線段的積相等,則四點共圓,及圓冪定理的逆定理等方法。
三、 四點共圓的在習題中的應用
【例1】如圖4,△ABC和△ADE中,∠BAC=∠DAE=54°,AB=AC,AD=AE,連接BD、CE交于F,連接AF,則∠AFE的度數是

圖4
( )
A.63° B.62° C.57° D.56°
方法一:如圖5,過點A作AG⊥BD,AH⊥CE。因為∠BAC=∠DAE=54°,所以∠BAC+∠CAD=∠DAE+∠CAD,所以∠BAD=∠CAE,
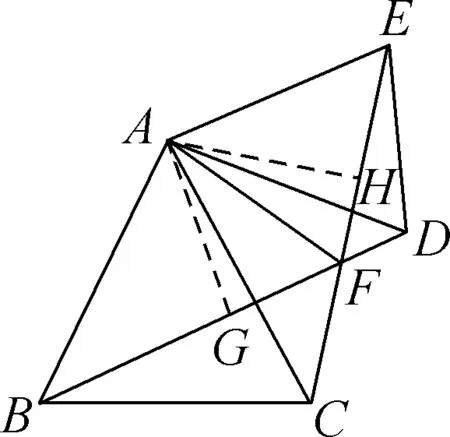
圖5


點評:本題是典型的手拉手模型可以利用8字形和角平分線的判定解決,但是難度比較大,尤其是作AG和AH兩條輔助線較難想到,學生難以挖掘出AF平分∠BFE這個結論。而利用四點共圓的方法,省去了添加輔助線使得復雜的推理變得容易發現,解題方法簡單了很多。
【例2】(2015年遼寧·撫順)如圖6,在Rt△ABC中,∠BAC=90°,過點B的直線MN∥AC,D為BC邊上一點,連接AD,作DE⊥AD交MN于點E,連接AE。
圖6
(1)當∠ABC=45°時,求證:AD=DE;
(2)當∠ABC=30°時,線段AD與DE有何數量關系?并請說明理由;
(3)當∠ABC=α時,請直接寫出線段AD與DE的數量關系。(用含α的三角函數表示)
方法一:(1)如圖7,過點D作DG⊥BC,交AB于點G,則∠BDE+∠GDE=90°,因為DE⊥AD,所以∠GDE+∠ADG=90°,所以∠BDE=∠ADG,因為∠BAC=90°,∠ABC=45°,所以∠C=45°,因為MN∥AC,所以∠EBD=180°-∠C=135°,因為∠BGD=45°,DG⊥BC,所以∠BGD=∠BDG=45°,BD=DG,所以∠AGD=135°,∠EBD=∠AGD,所以△BDE≌△GDA(ASA),所以AD=DE。
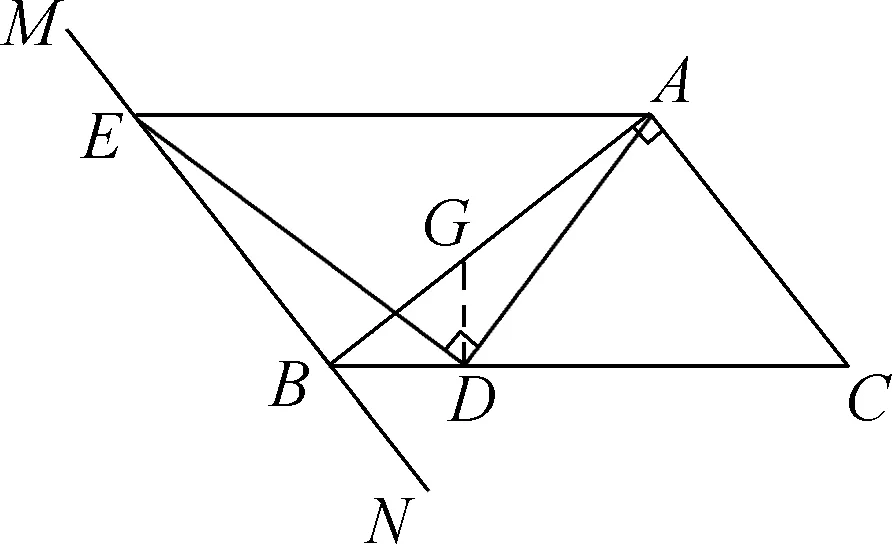
圖7

(3)AD=DE·tanα;

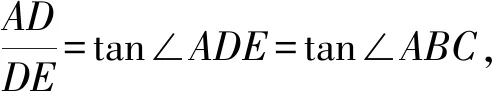
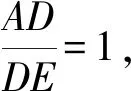
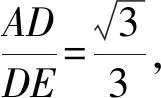

點評:方法一(2)(3)兩問作法太復雜,中考時時間有限很難做出來,方法二運用四點共圓的方法使得復雜的推理變得簡單明了,一氣呵成簡單得多同時還有助于我們發現題目各條件之間的內在聯系。
四、 結論
圓這一章的知識綜合性很強,可以將前面所學過的所有的圖形放在圓中研究問題,故四點共圓的基本理念可以將三角形、四邊形的相關知識進行轉化,有效結合幾何圖形,建立圖形變換的基本思想。我們做的很多題,可以不用四點共圓也能解出,但是比較復雜。四點共圓往往可以另辟蹊徑,在考場上如果一時想不出普通解法,四點共圓可以江湖救急。還有些題,不用四點共圓也能做但非常麻煩,我們在考場上要懂得“惜時如金”。

