探討“問題提出”教學的一般模式——基于“乘法分配律”的課堂分析

許天來，蔡金法

探討“問題提出”教學的一般模式——基于“乘法分配律”的課堂分析

許天來1，蔡金法2

（1．廣州大學 數學與信息科學學院，廣東 廣州 510006；2．特拉華大學 數學系，特拉華 紐瓦克 19716）

結合“乘法分配律”的課堂實例探討“問題提出”教學的一般模式，包括：（1）教師呈現問題情境；（2）教師根據教學目標設置恰當的引導語；（3）學生以個體方式或小組方式提出問題；（4）師生對學生所提問題進行“分析”“選取”“排序”和“求解”．一節課可能包含多個類似的問題提出教學活動．盡管“乘法分配律”的課堂設計遠早于問題提出教學一般模式的呈現，但是該課例很符合此一般模式．研究表明了研究和實踐的交互作用：通過研究問題提出的一般模式指導問題提出教學，同時問題提出教學的實踐促進了一般模式的研究．

問題提出；教學模式；引導語；乘法分配律；P-PBL

1 問題提出

數學問題提出（Mathematical Problem Posing）的研究在過去幾十年得到了較大的發展[1]．然而，問題提出融入數學課堂遠未實現常態化．當前關于問題提出教學研究的關鍵問題在于如何幫助教師更好、更多地將問題提出整合到課堂教學．除了要不斷進行培訓以提高教師運用問題提出進行教學的信念，更重要的是要對問題提出教學的一般模式進行探討，幫助教師理解問題提出教學的過程，增加其運用問題提出進行教學的信心和實踐．

2 研究框架

蔡金法基于對運用問題提出進行數學教學的研究，總結出基于問題提出的教學模式（Problem-Posing-Based Learning instructional model，P-PBL教學模式）[2]，如圖1．此模式描述了用單個問題提出任務進行教學的流程，詳見文[2]．步驟1和步驟2通常是同時呈現的，但在這個模式中將其分開討論，是為了強調在設計問題提出的教學任務時，問題情境和引導語同樣重要．首先，教師呈現問題情境，這個情境可以是數學情境、生活情境以及其它情境（如科學實驗情境或體育情境）[3-5]．其次，在呈現問題情境的同時，應當根據教學目標設置恰當的引導語，對學生所提問題的數量、難度、所涉及的知識領域等提出具體的要求．比如：（1）提出能夠對你的同學或老師有一定挑戰的數學問題；（2）提出涉及百分比的數學問題；（3）提出3個數學問題，簡單、中等難度和較難的各一個；（4）提出盡可能多的數學問題；（5）模仿范例中的問題，提出類似/不同結構的問題；（6）你能提出哪些至少包含2種運算的數學問題；（7）提出現實生活中能用此方程求解的數學問題；（8）提出兩個能用加、減法解決的數學問題，并讓黑板上的3個數同時出現在你的問題里[5]．再次，學生根據教師設置的情境和引導語，可以自己提出數學問題，也可以在小組中自己先提出數學問題，與組內同學交流與辯論，然后以小組的形式推選出最具代表性、最好的若干問題．最后，師生對學生所提問題進行恰當地處理，主要包含以下4個環節：（1）師生分析學生所提問題，包括對問題進行糾錯與完善，以及對重復、無序的問題進行分類；（2）選取難度適中、契合教學目標的問題；（3）確定求解問題的順序；（4）求解問題．

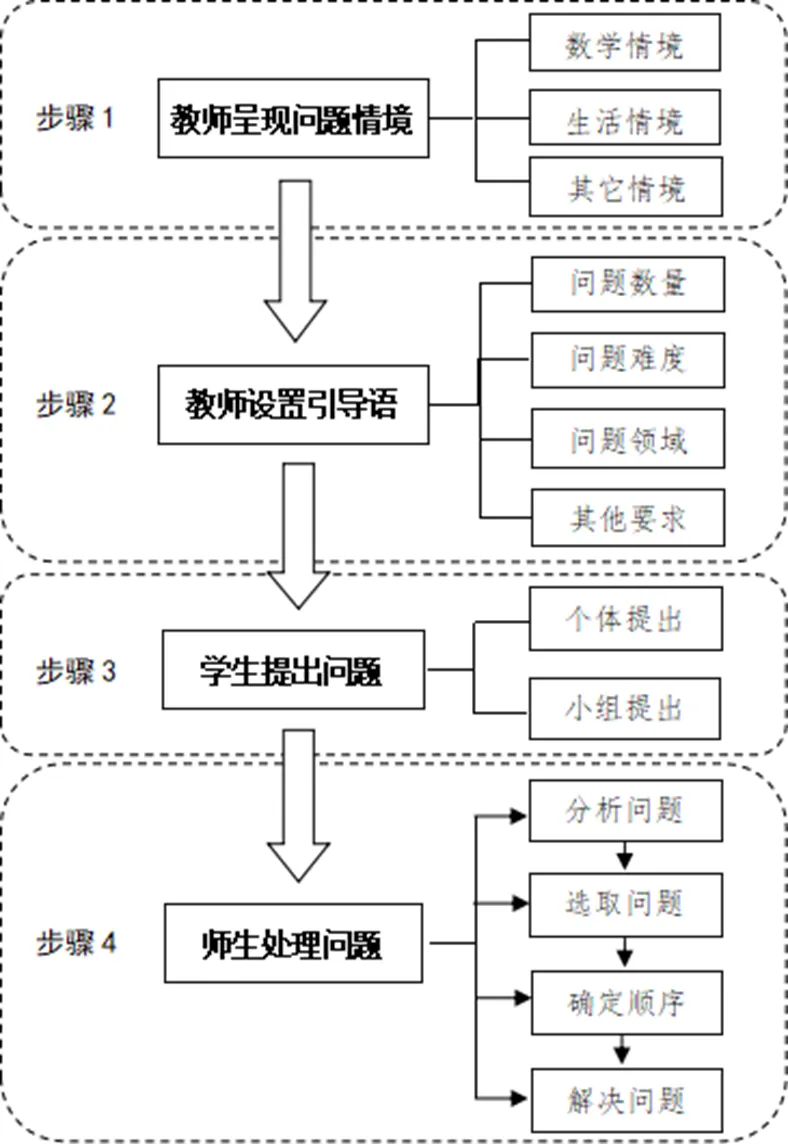
圖1 基于問題提出的教學模式

需要指出的是，一節課可能包含多個問題提出的教學活動，對應的課堂上亦會經歷多個類似的教學流程．莫延安和王濤在上述研究的基礎上，結合多個小學數學教學實例對其中的教學步驟進行了詳盡解讀[5]．研究結合基于問題提出進行教學的一個具體課例，對如何更好地運用這一教學模式展開進一步的論述．蔡金法等提出了教學理論和教學實踐的雙向關系[6]．其中，為了教學的理論（theory for teaching）是指旨在為學生創造更多更好的學習機會提供指導的理論；為了理論的教學（teaching for theory）是指通過教與學不斷地為提升和發展理論提供素材．如果說為了教學的理論指的是為了更好地教學和促進學生學習的理論，那么為了理論的教學則指的是有意設計用于生成、闡述和測試理論的教學．研究旨在強調教學理論與教學實踐間的雙向關系的重要性．

3 研究對象

研究對象為小學數學特級教師丁老師2016年基于問題提出教學“乘法分配律”的課例[7]．此課例在大型優質課評比活動中獲得一等獎，是丁老師在特拉華大學蔡金法的建議和指導下，勇于突破教學舒適區，克服對失去課堂掌控的恐懼，從零開始深入學習，掌握基于問題提出的教學方法并首次基于問題提出進行的教學嘗試[8]．整體教學過程如表1．

表1 “乘法分配律”總體教學過程

可以看出，課例可劃分為5個環節，具體為創設懸念、問題提出、點子圖、探索歸納和練習回顧．第一，設置懸念，引導學生思考為何丁老師算得這么快．第二，要求學生根據算式提出生活中的數學問題，幫助他們從這些數量眾多的、來自“自己的”例證中初步感受乘法分配律的合理性．這種解決“自己的”問題，加上小組“競賽”的氣氛，能很好地調動學生學習的積極性．在解決問題的過程中，引發學生產生連續、愈加強烈的認知沖突——“為什么兩種形式的算式可用以解決同一問題？”“為什么兩種形式的算式可用以解決所有問題？”第三，結合“點子圖”，幫助學生將具有“分”“合”特征的算式聯想成自己所提出的數學問題，促進學生通過數形結合理解乘法分配律．第四環節則通過讓學生補充等式，引導其從特殊到一般驗證規律，結合符號進行歸納．最后，精心設計習題，呼應前文疑問，總結全課．

綜上所述，丁老師的課例僅包含一個問題提出活動．下面將結合此課例具體的教學片段，探討“問題提出”教學的一般模式．

4 研究結果和討論

4.1 關于教師呈現問題情境

第一個流程和第二個流程往往是同時呈現的．P-PBL教學模式將它們分開，是為了強調在運用問題提出進行教學設計時，情境和引導語同等重要．

【教學片段1】

師：咱們班的同學個個都是編題高手，現在把難度升級，如果只給你算式，你能根據算式提出生活中的數學問題嗎？

生：能！

師：謝謝你們自信的回答．這樣吧！丁老師把全班分成兩大組，第1、2組的同學請根據“算式1”，第3、4組則根據“算式2”，來提出現實生活中的數學問題并清楚地記錄下來．（老師故意把兩個算式隱藏起來，不讓第1、2組和第3、4組的同學分別知道對方的算式．）

學生活動：第1、2組編：(5+7)×4；第3、4組編：5×4+7×4．

評析：運用問題提出進行教學，首先應選擇恰當類型的任務情境引導學生提出數學問題，主要分為數學情境、生活情境和其它情境，教師可根據不同的學情和教學目標選取不同類型的情境．數學情境包括算式、方程、幾何圖形、表格、函數圖象、模式（滿足特定規律的一組數字或圖形，如斐波那契數列和三角點陣）等．教師可要求學生根據“純”數學情境（如算式和方程）提出生活中的問題，以此幫助學生結合熟悉的生活場景探究抽象的數學知識．生活情境則體現了數學在現實中的運用，貼近學生日常生活實際，具有一定的趣味性．要求學生根據生活情境提出數學問題，可以幫助他們從熟悉的場景中提煉數學關系．其它情境包括科學實驗情境和體育情境等學生相對陌生的場景．

在丁老師的教學片段一中，算式“(5+7)×4”和“5×4+7×4”均是“純”數學情境，相比教師直接給出問題讓學生求解，這種學生“自己的”問題更貼合其生活實際，學生可以結合生活中的所見所聞探究抽象的乘法分配律，教師在此基礎上展開教學能更好地幫助學生理解所學內容．

4.2 關于教師設置引導語

在上述教學片段一中，丁老師設置的引導語為：“提出現實生活中的問題”，并未提出其它要求．一方面是因為數學表達式的“結構較為穩定”，另一方面是因為教學的重點在于幫助學生理解兩種形式的算式均可用以求解同一問題．在其它情境如“斐波那契數列”中，如若不通過引導語進行限制，學生可能會為了追求數量而未能集中精力進行更高層次的思維參與．因此，教師可以設置以下引導語：“（已知數列1，1，2，3，5，…，此數列前兩項為1，從第三項開始，每一項都等于前面兩項之和）你能根據這個情境提出一個簡單的數學問題、一個中等難度的數學問題和一個較難的數學問題嗎？”

由上可知，設置問題提出的任務包括問題情境類型的選取以及引導語的設計兩個方面．因此，為了更好地設置問題提出任務從而為學生提供更多的學習機會，教師在備課階段應對學生可能會提出的問題進行預測．首先，教師自己應當能提出盡可能多的、不同類型的數學問題，這有助于教師更好地預測學生可能會提出的正確問題，從而選擇恰當的情境類型進行教學．在這個課例中，算式情境是一種“結構較為穩定”的情境，教學實踐表明，學生所提問題總體上在丁老師的預料范圍內．

其次，教師還應當能較好地預測學生可能會提出的數學問題，包括正確的、錯誤的數學問題甚至是非數學問題，以進行針對性的教學準備．研究表明，中國教師在預測學生所提問題的準確率上存在著極大的個體差異（7%～89%）[9]．對于具體的問題提出任務，可以通過問卷的形式收集盡可能多的師生所提問題，尤其應注意選取同年齡段、學情相近的學生作為調查對象．如此才能更好地預測學生可能會提出的問題，在備課階段提前準備應對策略．在有了充分的準備后，如若學生在課堂上提出教師課前未預料到的數學問題，后者可以有更多的時間思考處理對策．

4.3 關于學生以個體形式或小組形式提出數學問題

教師在呈現問題情境并設置引導語后，學生開始提出數學問題．

【教學片段2】

師：剛才同學們都討論得很熱烈，編得很起勁．下面哪個小組來展示一下你們組編的數學問題．

展示第3、4組根據5×4+7×4編的部分數學問題（如圖2所示）．

師：請一位小組長來讀讀你們組編的數學問題．（生讀上述“買牛奶問題”．）

小組長（故作神秘）：我請坐在第1、2組的同學來猜猜看，我們是根據哪一道算式來編的？

生1：(5+7)×4．

生2：我認為是5×4+7×4．

師（追問）：真是奇怪了，剛才有的同學猜的卻是(5+7)×4，這到底是怎么一回事？誰來說說其中的道理？

生3：(5+7)×4是先算“一瓶普通牛奶和一瓶脫脂牛奶的價錢是12元”，再乘4，就可以算出“各買4瓶共花的錢”；而5×4+7×4是先分別算出“4瓶普通牛奶的價錢”和“4瓶脫脂牛奶的價錢”，再把它們加起來，都是一樣的．

生4：我還發現，它們的得數也是相同的，這兩個算式都可以解決剛才這個小組編的數學問題．

師：原來如此！

圖2 學生提出的數學問題

評析：P-PBL教學模式的第三個流程為學生以個體方式或小組方式提出數學問題．學生可以在小組中先自己提出數學問題，與組內同學進行交流與辯論，以小組的形式推選出最具代表性、最好的若干問題．以小組為單位，課堂所解問題隸屬更多學生，小組間的良性“競爭”能較好地激發學生學習的主動性．在小組討論的過程中，學生不僅進行了個人積極的主動建構，還參與了社會性的溝通過程，有助于達成更有意義的學習[10]．教師也可以讓學生自己提出數學問題，從而在有限的課堂時間內留給學生更多獨立思考的時間．

在此課例中，丁老師將學生分成兩大組，分別根據乘法分配律兩種不同形式的算式之一編制問題．在此基礎上丁老師要求每組學生通過討論交流，在規定時間內提交最好的幾個問題，因此，不同水平的學生都能充分參與到問題提出活動之中．值得注意的是，在此課例中，并不知道學生是如何根據算式提出數學問題的．

此外，丁老師通過分組“競爭”的形式促進學生積極思考．在第1、2小組學生中，至少猜中1種算式的學生包含以下4種情形．第一，未發現此問題可用給定算式(5+7)×4進行求解，自行得到另一算式5×4+7×4；第二，發現此問題可用給定算式進行求解，未進行其它思考．第三，發現可用給定算式求解，但由于小組之間的“競爭”關系，認為教師不會給兩個小組同一算式，通過積極的思考仍未能想出另一算式．第四，發現可用給定算式求解，最終通過積極的思考得到另一算式．無論何種情形，在教師讓學生結合生活情境做出解釋后，都能引發學生產生強烈的認知沖突：“為什么兩種形式的算式都可用以解決同一問題？”特別對于后兩類學生，他們在此之前已進行了積極主動的思維參與．相比直接求解教師提供的問題，運用問題提出進行教學的這部分學生尋求第二解法的意愿更為強烈．

4.4 關于師生處理問題

課堂上師生應對學生所提的數學問題進行恰當的處理．

【教學片段3】

前略，與上述片段類似，僅僅是兩個小組提問與猜測角色的互換．

師（小結）：雖然這兩個算式“長”得不一樣，但都可以同時解決這個數學問題（一套書上冊5元，下冊7元，小明買了4套，一共花了幾元？）．千金難買回頭看！剛才你們小組編的數學問題，是不是都可以用黑板上的這兩個算式來解決？

（給學生一點時間去靜靜地觀察和思考．）

生（齊答）：是的．

師：哇！看來這兩個算式真的很神奇．丁老師有一個圖更神奇，它可以把大家編的數學問題全部都表示出來，信不信？（學生半信半疑）

評析：丁老師點評學生所提問題，包括表達是否簡潔準確、是否符合生活實際等．她讓兩個小組提問與猜測的角色進行互換，由于有前面教學的鋪墊，第3、4組學生很容易發現第1、2組學生所提問題同樣可根據兩個算式進行編制．教師進而通過追問的方式引導學生思考：“這些問題是不是都可以用黑板上的兩個算式來解決？”以此激發學生產生認知沖突：“為什么兩種形式的算式均可用以解決所有問題？”很自然地過渡到第三環節的教學——通過點子圖幫助學生更好地理解乘法分配律．結合此前第3、4組展示和第1、2組猜測的教學處理，這種連續的、愈發強烈的認知沖突，能提供學生更多的學習機會，更能調動學生積極主動的思維參與．

5 結論

“問題提出”教學的一般模式有助于教師更好地了解如何運用問題提出進行教學，從而提高其教學信念，最終促成問題提出教學更多、更好地融入到數學課堂，為學生提供更多的學習機會．蔡金法和他的合作者認為，盡管現有的多個小學教學案例（包括此文中的案例）充分驗證了P-PBL教學模式的有效性[11-13]，但仍需結合更多的案例對其進行驗證、細化和修改[2]．另一方面，這一教學模式也可作為教師開發P-PBL教學案例的理論指導．結合P-PBL教學模式發現，教師學習運用問題提出進行教學應從學習設置教學任務開始，包括問題情境的類型與引導語．此為教師引導學生提出問題和隨后師生處理問題的基礎．

最后需要說明的是，運用“問題提出”進行教學，并不是要取代基于“問題解決”的教學等傳統手段，而是作為一種創新，通過恰當的問題提出活動更好地激發學生學習數學的興趣，引發其產生強烈的認知沖突以突破教學重難點，最終幫助學生達成對數學知識的概念性理解．當教師在教學設計階段判斷出基于問題提出的教學方式也許能為學生提供更多的學習機會，則可以大膽付諸實踐，做探究型教師．

[1] 賈隨軍，姚一玲．問題提出的回顧與展望——美國特拉華大學終身教授蔡金法訪談錄[J]．教學月刊小學版（數學），2021（10）：8-13．

[2] CAI J. What research says about teaching mathematics through problem posing [J]. éducation & Didactique, 2022, 16 (3): 31-50.

[3] 蔡金法，許天來．數學問題提出的例子、類型和內涵[J]．小學教學（數學版），2019（7-8）：34-40．

[4] CAI J, HWANG S. Making mathematics challenging through problem posing in the classroom [M] // LEIKIN R, CHRISTOU C, KARP A, et al. Mathematical challenges for all. New York: Springer, 2023: 115-145.

[5] 莫延安，王濤．小學數學“問題提出”教學步驟解讀[J]．教育研究與評論（小學教育教學），2023（2）：59-66．

[6] CAI J, HWANG S, MELVILLE M, et al. Theory for teaching and teaching for theory: Artifacts as tangible entities for storing and improving professional knowledge for teaching [M] // PRAETORIUS A K, CHARALAMBOUS C Y. Theorizing teaching: Current status and open issues. Cham: Springer, 2023: 225-251.

[7] 丁玉華，曾令鵬．“乘法分配律”教學實錄與評析[J]．小學數學教育，2017（21）：43-46．

[8] CHEN T, CAI J. An elementary mathematics teacher learning to teach using problem posing: A case of the distributive property of multiplication over addition [J]. International Journal of Educational Research, 2020 (102): 101?420.

[9] XU B, CAI J, LIU Q, et al. Teachers’ predictions of students’ mathematical thinking related to problem posing [J]. International Journal of Educational Research, 2020 (102): 101?427.

[10] 蔡金法，姚一玲．數學“問題提出”教學的理論基礎和實踐研究[J]．數學教育學報，2019，28（4）：42-47．

[11] ZHANG H, CAI J. Teaching mathematics through problem posing: Insights from an analysis of teaching cases [J]. ZDM, 2021, 53 (4): 961-973.

[12] 陳婷，徐紅，徐冉冉，等．數學教師學習使用“問題提出”教學法的個案研究——以“用字母表示稍復雜的數量關系”為例[J]．數學教育學報，2019，28（2）：7-12．

[13] 徐冉冉，裘曉麗，姚一玲，等．基于教師—研究者伙伴關系的初中數學教學改進——以“一次函數”“問題提出教學”為例[J]．數學教育學報，2021，30（1）：25-31．

Exploring the Problem-Posing Based (P-PBL) Instructional Model——An Analysis of a Teaching Case Involving the Distributive Law of Multiplication over Addition

XU Tian-lai1, CAI Jin-fa2

(1. School of Mathematics and Information Science, Guangzhou University, Guangzhou Guangdong 510006, China;2. The Department of Mathematics, University of Delaware, Delaware Newark 19716, USA)

Using a classroom example of a problem-posing teaching case involving the distributive law of multiplication over addition, this study discusses the general pattern of problem-posing instruction. The pattern includes the following steps: (1) The teacher presents a problem-posing situation; (2) the teacher provides a problem-posing prompt along with the problem situation, that is, sets up the appropriate guiding language according to the teaching objectives; (3) the students pose problems either individually or in groups; and (4) the teacher and students analyze, select, sort, and solve the problems posed by the students. A single class session might encompass multiple instances of similar problem-posing instructional activities. Although the lesson involving the distributive law of multiplication over addition predates the formal presentation of the general problem-posing instructional pattern, the example aligns well with this pattern. This paper further underscores the interplay between research and practice: Research on the general pattern of problem-posing instruction guides its implementation whereas the practical application of problem-posing instruction advances research on the general pattern.

problem posing; teaching model; problem-posing prompt; distributive law of multiplication over addition; P-PBL

G623.5

A

1004–9894（2023）05–0017–04

許天來，蔡金法．探討“問題提出”教學的一般模式——基于“乘法分配律”的課堂分析[J]．數學教育學報，2023，32（5）：17-20．

2023–08–21

西南大學引進人才計劃項目（SWU118118）

許天來（1990—），男，廣東博羅人，博士生，主要從事數學教育研究．蔡金法為本文通訊作者．

[責任編校：張楠、陳雋]