考慮剛度和質量耦合效應的結構彈性成像方法1)

付君健 彭鐵川 李 然*,2) 李帥虎 周祥曼 李 響

* (水電機械設備設計與維護湖北省重點實驗室,湖北宜昌 443002)? (三峽大學機械與動力學院,湖北宜昌 443002)

** (長江三峽通航管理局,湖北宜昌 443002)

??(武漢理工大學交通與物流工程學院,武漢 430063)

引言

彈性成像[1-3]是一種醫學影像技術,可以把生物體組織的彈性模量信息轉換為可視化圖像,顯示組織或器官病理變化的位置和大小.對于機械裝備結構,損傷會導致結構特定部位彈性模量發生改變,繼而使結構力學性能發生改變.如果將彈性模量與機械結構損傷表征關聯,可以通過彈性成像方法獲取彈性模量分布以實現結構的損傷識別.機械裝備結構極易產生缺損、夾雜、結冰和積水等多種損傷,而大多數損傷本質上是結構特定部位的彈性模量發生偏移.因此,研究一種先進的彈性成像方法可實現結構多種損傷類型的全局識別,有助于實現重大機械工程裝備的服役安全評價.

目前,結構損傷識別方法主要分為先進成像方法和模型修正方法.先進成像方法是一種無損檢測技術,它通過計算機分析處理穿越物體的響應信號,并融合相應算法重構物體內部信息,從而以圖像的形式直觀顯示物體的損傷位置.近年來,許多先進成像方法被用于結構損傷識別,如超聲成像[4]、射線成像[5]等.先進成像方法可以對結構進行實時成像,具有損傷直觀可視等優點.但大多數成像方法屬于局部區域損傷識別技術,需要知道損傷大致區域作為先驗信息,對機械結構的損傷識別效率較低.為解決局部損傷識別方法的缺陷,具有全局識別能力的模型修正方法應運而生.模型修正方法以有限元模型為基礎,首先定義一組表征損傷位置和程度的修正參數,修正參數如單元剛度折減系數、截面面積和邊界條件等,然后通過修正損傷結構的有限元模型將模型響應和實測響應之間差異最小化,最后找到修正參數的最優解得到結構的損傷位置和程度[6-8].模型修正方法對于損傷識別算法、響應、參數的研究較為系統.但大部分模型修正方法僅針對單一損傷類型識別,并且結構的損傷位置和程度僅通過數值顯示,直觀可視化效果較差[9].而彈性成像方法融合了先進成像方法和模型修正方法的優勢,無需任何先驗信息,可以從圖形角度反映結構全局區域的損傷位置和程度,對結構損傷的幾何描述具有較強的直觀性.

拓撲優化[10-12]與彈性成像類似,其本質是通過將設計變量與彈性模量耦合實現對整體結構性能的調控.針對拓撲優化,單元密度為1 的單元對結構性能貢獻最大,單元密度接近0 的單元對結構性能貢獻最小.針對損傷識別,單元密度為1 的單元對應實體結構無損傷區域,單元密度小于1 的單元對應實體結構損傷區域.拓撲優化與損傷識別都是為了找到滿足目標函數的彈性模量空間分布.因此,拓撲優化也可以用于結構損傷識別.從損傷表征層面,目前基于拓撲優化的損傷識別方法主要采用水平集法[13-14]、移動變形組件法[15-16]和變密度法[17].水平集法通過水平集函數隱式描述結構,其中零水平集表征結構損傷的邊界[18].移動變形組件法通過組件的移動、旋轉等方式實現結構的變化,采用拓撲描述函數描述結構,拓撲描述函數值大于0 表示有組件區域,拓撲描述函數值小于0 表示缺損區域[19].變密度法通過單元密度函數描述結構,單元密度為1 表示實體結構無損區域,單元密度接近0 表示實體結構缺損區域[20].水平集法對于損傷幾何形狀的描述能力強,但一般用于反演結構孔洞損傷的形狀[21].對于基于水平集法或移動變形組件法的損傷識別方法,損傷數量需提前預估,初始孔洞或組件數量會影響到最終反演結果[22].從損傷識別目標函數構建層面,其構建可采用靜力響應和動力響應數據.靜力響應一般包括位移、應變和應力等.然而在實際工程問題中,損傷會導致結構剛度、質量發生改變,而結構的靜力響應無法反映結構質量特性的變化,并且靜力響應難以測量.但結構的動力響應容易通過傳感器測量[23],能同時反映結構剛度、質量特性的變化,并且動力響應在結構發生損傷的早期階段更加敏感.動力響應的響應類型一般分為頻率[24]、振型[25]、頻響函數[26]等.在靜力響應和動力響應下,基于拓撲優化的損傷識別方法都表現出了較好的損傷識別效果[27].

上述研究對于損傷的表征比較單一,均只針對實體結構中造成結構剛度和質量減小的損傷類型(缺損、夾雜).然而在航空航天領域中,由于復雜自然環境[28-29]及各種意外情況[30]的影響,機械裝備結構除會產生造成剛度和質量減小的損傷類型(缺損、夾雜)外,具有多孔特征的結構[31-32]還會產生結冰或積水損傷,這兩類損傷類型分別會造成結構剛度和質量增大、結構僅質量增大.大多數損傷會造成結構彈性模量發生改變.因此,研究一種以拓撲優化驅動彈性成像的方法,實現結構缺損、夾雜、結冰、積水多種損傷類型的全局識別,對于豐富彈性成像理論內涵和實際工程應用具有重要意義.

本文提出了一種考慮剛度和質量耦合效應的結構彈性成像方法.首先,構建缺損、夾雜、結冰和積水多種損傷類型的統一表征.其次,構建損傷表征、力學模型和特征值響應之間的映射關系.再建立基于特征值響應的彈性成像模型,并建立彈性成像反演的數值實施方式.最后,分別考慮缺損、結冰、積水3 類損傷,探討對二維結構進行彈性成像實現損傷識別的有效性,并探討三維結構彈性成像問題驗證本方法的通用性.

1 多種損傷類型的統一表征

為了解決結構缺損、夾雜、結冰和積水多種損傷類型的全局識別問題,關鍵在于建立不同損傷類型的統一表征.在損傷表征過程中,損傷會造成結構剛度和質量發生改變,并且不同損傷類型對結構剛度和質量的影響不同.例如,缺損和夾雜會同時造成結構剛度和質量減小,結冰會同時造成結構剛度和質量增大,積水不會影響結構剛度但會造成結構質量增大.彈性模量僅能反映結構剛度變化,單一的彈性模量不足以表征多種損傷類型,因而還需引入能反映結構質量變化的參數,構建同時考慮結構剛度和質量效應的損傷表征.受動力學拓撲優化理論啟發,本文以結構離散單元的彈性模量系數和材料密度系數作為成像參數,將成像參數與彈性模量、材料密度關聯,構建考慮結構剛度和質量耦合效應的損傷表征.結構的損傷類型可分為以下3 類:

(1)第1 類損傷類型(缺損、夾雜): 損傷同時造成結構的剛度和質量減小,繼而導致成像參數減小;

(2)第2 類損傷類型(結冰): 損傷同時造成結構的剛度和質量增大,繼而導致成像參數增大;

(3)第3 類損傷類型(積水): 損傷對結構剛度無影響,僅造成結構質量增大,繼而導致成像參數增大.

基于以上分類,定義彈性模量系數x和材料密度系數y兩種成像參數,建立成像參數與損傷表征的數學模型.如圖1 所示為多種損傷類型表征,在同一套有限元網格定義了兩套成像參數,第一套成像參數xj針對彈性模量,第二套成像參數yj針對材料密度,兩套成像參數可反映不同損傷類型對結構剛度和質量的影響.

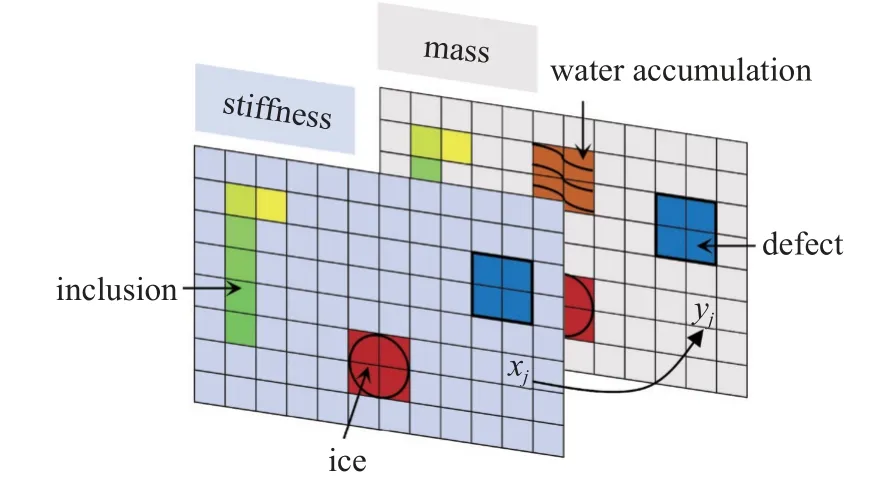
圖1 多種損傷類型表征Fig.1 Characterization of damages

式中,x和y為成像參數,x和y最小值取0.001 為避免剛度和質量矩陣奇異.當無損結構為實體結構時,b取值為1;當無損結構為具有多孔特征的結構時,b取值范圍為 0.001 ≤b＜1.

基于拓撲優化理論的固體各向同性材料懲罰模型(solid isotropic material with penalization,SIMP)[33],分別構建成像參數x(彈性模量系數)與彈性模量、成像參數y(材料密度系數)與材料密度的非線性插值模型如下

式中,E0為實體材料的彈性模量,E為單元彈性模量,ρ0為實體材料的密度,ρ 為單元材料密度.p和q為懲罰指數,其可加快優化模型收斂,然而在動力學問題中,p＞q這個條件會導致在拓撲優化過程中產生局部模態,有研究提出采用更大的質量懲罰指數 (p＜q) 可以控制局部模態[24],因此本文設置p＜q.

2 損傷對結構性能的影響

為了考慮損傷對結構性能的影響,將成像參數嵌入到無阻尼自由振動系統的有限元模型.

將結構離散為n個單元,則

式中,x,y為結構成像參數矩陣.

單元剛度、質量矩陣可寫為

式中,Kj為第j個單元的剛度矩陣,B為應變位移矩陣,D為結構材料彈性矩陣,為實體材料單元剛度矩陣,Mj為第j個單元的質量矩陣,N為形函數矩陣,為實體材料單元質量矩陣,Ω 表示結構域,Ωj表示第j個單元的結構域.

全局剛度、質量矩陣可表示為

式中,K為關于成像參數x的結構全局剛度矩陣,M為關于成像參數y的結構全局質量矩陣.

進一步構建損傷表征、力學模型和特征值響應之間的映射關系,首先對結構無阻尼自由振動系統進行有限元分析,得到無阻尼自由振動系統的有限元平衡方程

式中,x,y為成像參數矩陣,λi為第i階特征值,其中λi=ωi2,ωi為第i階固有圓頻率,ωi=2πFi,Fi為第i階特征頻率,φi為第i階特征向量.

3 基于特征值響應的彈性成像建模與求解

3.1 彈性成像模型

特征值響應是最容易得到的模態參數之一,在建立彈性成像模型時,本文僅考慮結構特征值響應.當使用特征值作為響應參數進行損傷識別時有以下兩個特點[35]: (1)當損傷出現在對稱結構的對稱位置時,可能會引起特征值響應的變化量相同;(2)結構各階特征值響應對各處損傷的敏感性不同.因此,為避免損傷識別結果出現多解的問題,提高損傷識別精度,應適當選用多階特征值構造彈性成像目標函數.本文以數字模型和真實結構模型的特征值響應變化率的平方和為目標函數,以有限元平衡方程和成像參數上下限為約束條件,構建如下結構彈性成像模型

式中,x,y分別為元素取值在之間的成像參數矩陣,xmin和xmax分別為成像參數xj可取的最小值和最大值,ymin和ymax分別為成像參數yj可取的最小值和最大值,其中xmin,xmax,ymin和ymax的取值由式(1) 可知,n為成像參數的數量,f(x,y) 表示彈性成像目標函數,m為模態階數,wi為第i階特征值的權重,權重總和為1,λi為數字模型的特征值響應,λi*為真實結構模型的特征值響應.特征值權重是可調參數,通過改變特征值權重可靈活調整各階特征值對損傷識別的敏感性.

3.2 靈敏度分析

為了求解彈性成像模型,本文推導了目標函數關于成像參數的導數.

對目標函數關于單元成像參數xj,yj分別求導可得

對結構特征問題方程(11)關于單元成像參數xj和yj分別求導可得

式中,φi是 正則化后的第i階特征向量,T 代表矩陣轉置.

(1)當考慮對剛度和質量有耦合效應的損傷類型(第1 類或第2 類損傷類型)時,由式(1)可知y=x.將y=x代入式(13)～式(19)得到目標函數關于單元成像參數的導數為

其中,特征值關于單元成像參數的導數為

再將式(21)代入式(20)得到最終目標函數關于單元成像參數的導數為

(2)當考慮僅對質量有影響的損傷類型(第3 類損傷類型)時,由式(1)可知x=b,因此無需對單元成像參數xj求導.將x=b代入式(13)～式(19)得到目標函數關于單元成像參數的導數為

其中,特征值關于單元成像參數的導數為

由于K為常數,因此可得

此時特征值關于單元成像參數的導數為

再將式(26)代入式(23)得到最終目標函數關于單元成像參數的導數為

4 數值實施

圖2 所示為考慮剛度和質量耦合效應的結構彈性成像流程圖.本方法需獲得損傷結構的特征值響應,并作為唯一已知的輸入數據,結構內部損傷的位置、大小和數量均未知.為此,本文采用數值實驗替代實際實驗獲得損傷結構的特征值響應,通過在結構上開孔(預設缺損)或設置其他損傷,模擬可能存在的損傷結構,并通過有限元法計算損傷結構的特征值響應.然后求解數字模型(無損結構模型)的結構特征問題方程得到特征值和特征向量,并正則化特征向量用于之后靈敏度分析.之后,計算目標函數和進行靈敏度分析.再采用基于梯度的優化算法更新成像參數,通過式(42)的收斂準則判斷目標函數是否收斂,優化模型不斷迭代直至滿足收斂準則,最后輸出成像結果.

圖2 考慮剛度和質量耦合效應的結構彈性成像流程Fig.2 Structural elastography process considering the coupling effect of stiffness and mass

本文采用基于梯度的優化算法,考慮成像參數的約束條件,成像參數x和y的迭代更新策略分別如下

式中,r為迭代步數,α 為迭代步長,min 與 max 分別代表取括號中最小值與最大值.

然后將第r步敏度和第r+1 步敏度相加取平均值,以保持迭代曲線的穩定性

最終成像參數x和y的迭代更新策略分別如下

(1)當結構存在對剛度和質量有耦合影響的損傷類型(第1 類或第2 類損傷類型)時,由式(1)可知y=x,顯然此時h1=h2,因此成像參數的迭代更新策略可統一為

(2)當結構存在僅對質量有影響的損傷類型(第3 類損傷類型)時,由式(1)可知x為常數,因此x無需迭代更新.此時成像參數的迭代更新策略為

定義結構彈性成像模型的收斂準則如下

式中,ε 代表一個極小正數,rmax為最大迭代步數.

5 數值算例

本節通過4 個數值算例來驗證考慮剛度和質量耦合效應的結構彈性成像方法的有效性和通用性.在本節所有算例中,二維/三維實體結構的彈性模量E0=200 GPa,材料密度 ρ0=7800 kg/m3,泊松比ν=0.3(如無特殊說明,本文僅考慮各向同性材料),彈性成像模型的成像參數初始值為無損結構成像參數值.為了解決難以區分對稱結構對稱位置損傷的問題,需要在結構特定位置施加合適的非結構集中質量[36].

5.1 存在第1 類損傷類型的結構彈性成像

為驗證本方法識別結構中第1 類損傷類型(缺損)的有效性,定義圖3 所示的二維半MBB (Messerschmitt-B?lkow-Blohm)梁結構,初始無損結構為實體結構,結構域長寬比為2:1,長度為4 m,寬度為2 m,結構左端支撐約束,右下角支撐約束,結構被離散為80×40 個雙線性四邊形單元,在結構長度方向5/8 位置及寬度方向1/2 位置設置一個尺寸為0.6 m×0.6 m的缺損區域,缺損區域材料彈性模量和材料密度分別設置為0.001E0,0.001ρ0,在結構右下角位置節點上施加數值大小為結構域質量20%的非結構集中質量.本算例僅考慮結構前6 階特征值,特征值權重w=[0.25 0.15 0.15 0.15 0.15 0.15].

圖3 內置缺損的二維半MBB 梁結構Fig.3 Two-dimensional half-MBB beam structure with built-in defect

目標函數迭代曲線如圖4 所示,隨著優化的進行,目標函數值下降速度由快到慢,當彈性成像模型迭代287 步后目標函數值趨于平穩,結構成像圖中低成像參數值區域逐漸清晰.從圖4 中可以看出迭代曲線光滑,表明算法穩定性良好.在彈性成像模型經過616 次迭代后,得到如表1 所示的無損模型的特征頻率,并得到如圖5 所示的A 缺損結構的成像結果,成像結果下方顏色條的刻度值對應成像參數值.由表1 可知最終無損模型的前6 階特征頻率與損傷模型的前6 階特征頻率基本一致.為了方便將損傷識別結果與真實損傷區域進行對比,圖5 中黑色正方形邊線表示真實損傷結構的損傷區域邊界.由圖5 可知,最終成像結果顯示的損傷區域位置和大小與設定損傷區域基本一致.由于本文是基于變密度拓撲優化法構建了成像參數與彈性模量、材料密度的非線性插值模型,因而成像參數變量存在中間值,導致成像結果的邊界會存在模糊的過渡,故本方法對損傷形狀的成像是一種近似,無法嚴格識別出損傷的精準形狀.由于噪聲數據影響導致成像結果左下方出現些許高亮區域,但從成像結果中可以直觀看出高亮區域的成像參數值與損傷區域的成像參數值明顯相差較大,因此可以辨別出高亮區域不是損傷區域.

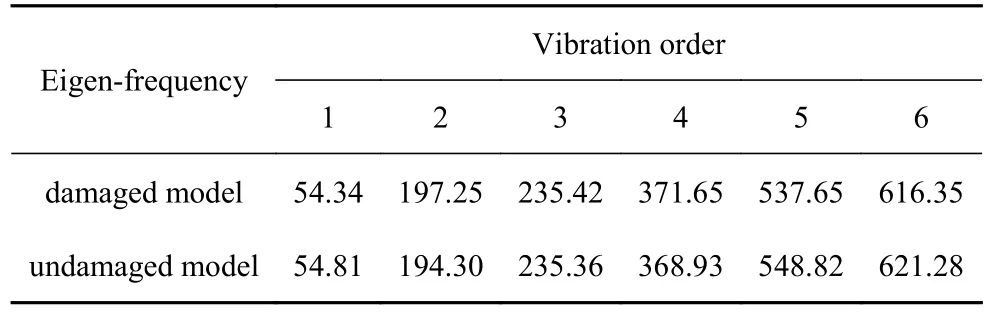
表1 算例1 中損傷模型和無損模型的特征頻率(Hz)Table 1 Eigen-frequencies of damaged model and undamaged model in the example 1 (Hz)

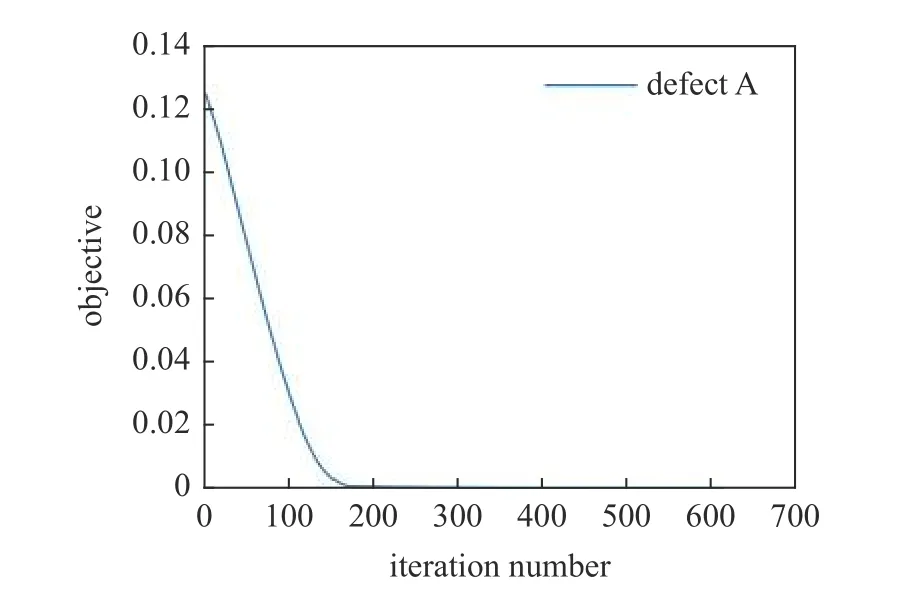
圖4 二維半MBB 梁結構彈性成像迭代曲線Fig.4 Iterative curve of elastography of two-dimensional half-MBB beam structure

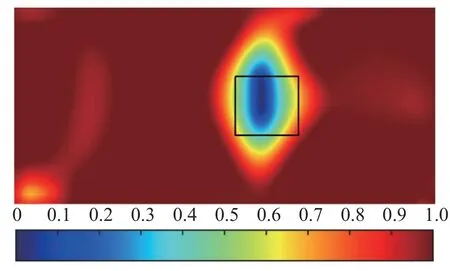
圖5 二維半MBB 梁結構成像結果Fig.5 Two-dimensional half-MBB beam structure imaging results

5.2 存在第2 類損傷類型的結構彈性成像

為驗證本方法識別結構中第2 類損傷類型(結冰)的有效性,定義如圖6 所示的二維懸臂梁結構,初始無損結構為具有多孔特征的結構,該結構由80×40 個多孔單胞構成,結構的彈性模量和材料密度分別設置為0.3E0,0.3ρ0,結構域長度為4 m,寬度為2 m,結構左端固定約束,結構被離散為80×40 個雙線性四邊形單元,在結構長度方向1/4 位置及寬度方向1/2 位置設置一個尺寸為0.6 m×0.6 m 的結冰區域,結冰區域的彈性模量和材料密度分別設置為E0,ρ0,在結構右上角位置節點上施加數值大小為結構域質量20%的非結構集中質量.本算例考慮與算例5.1 相同的特征值階次和特征值權重.

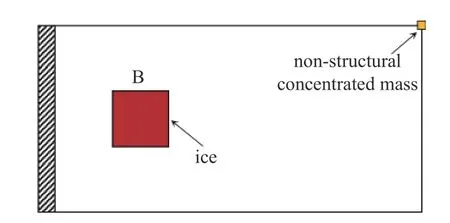
圖6 內置結冰的二維懸臂梁結構Fig.6 Two-dimensional cantilever beam structure with built-in ice

如圖7 所示,隨著優化的進行,目標函數值下降速度很快,彈性成像模型迭代157 步后目標函數開始趨于平穩,迭代900 步后滿足收斂準則,得到如表2 所示的無損模型的特征頻率,并得到如圖8 所示的B 結冰結構的成像結果.由表2 可知最終無損模型的前6 階特征頻率與損傷模型的前6 階特征頻率基本一致.成像結果中出現一個高成像參數值的區域,該區域為識別的結冰區域,與設定的結冰區域位置和大小近乎完全一致,表現出了良好的彈性成像效果.本算例采用與算例5.1 不同的邊界條件,結果表明在不同邊界條件下本方法仍具有良好的損傷識別效果.

表2 算例2 中損傷模型和無損模型的特征頻率(Hz)Table 2 Eigen-frequencies of damaged model and undamaged model in the example 2 (Hz)

圖7 具有多孔特征的二維懸臂梁結構彈性成像迭代曲線Fig.7 Iterative curve of elastography of two-dimensional cantilever beam structure with porous features

圖8 具有多孔特征的二維懸臂梁結構成像結果Fig.8 Imaging results of two-dimensional cantilever beam structure with porous features

5.3 存在第3 類損傷類型的結構彈性成像

為進一步驗證本方法識別結構第3 類損傷類型(積水)的有效性,如圖9 所示初始無損結構為具有多孔特征的結構,該結構由60×20 個多孔單胞構成,結構彈性模量和材料密度分別設置為0.3E0,0.3ρ0,結構長度和寬度分別為3 m,1 m,采用與算例5.1 相同的邊界條件,結構被離散為60×20 個雙線性四邊形單元,在結構長度方向3/10 位置和寬度方向3/4 位置、長度方向3/4 位置和寬度方向1/4 位置分別設置尺寸為0.2 m×0.2 m 的積水區域,由于積水僅影響結構質量,因此積水區域的材料彈性模量不變,材料密度設置為 ρ0.本算例施加非結構集中質量的位置和數值大小與算例5.1 保持一致,并且考慮與算例5.1 相同的特征值階次和特征值權重.

圖9 內置積水的二維半MBB 梁結構Fig.9 Two-dimensional half-MBB beam structure with built-in water accumulation

由圖10 可知,在彈性成像模型最初的幾步迭代中目標函數值迅速下降,然后目標函數值在彈性成像模型接下來的迭代步中下降變緩,最后目標函數值在彈性成像模型迭代165 步后趨于平穩.彈性成像模型迭代389 步后得到如表3 所示的無損模型的特征頻率,由表3 可知最終無損模型的前6 階特征頻率與損傷模型的前6 階特征頻率基本一致.圖11為彈性成像模型迭代389 步后結構的成像結果,從圖中可以看出,最終成像結果清晰,可以幾乎無偏差地識別出兩個積水區域各自的位置和大小,說明本方法用于多損傷條件下也具有良好的損傷識別效果.

表3 算例3 中損傷模型和無損模型的特征頻率(Hz)Table 3 Eigen-frequencies of damaged model and undamaged model in the example 3 (Hz)

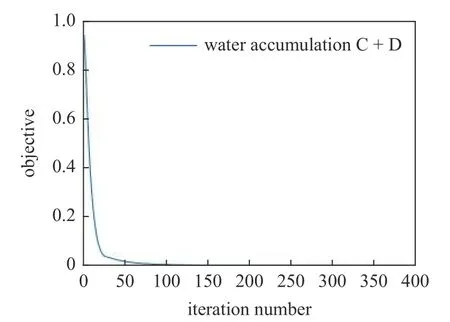
圖10 具有多孔特征的二維半MBB 梁結構彈性成像迭代曲線Fig.10 Iterative curve of elastography of two-dimensional half-MBB beam structure with porous features

圖11 具有多孔特征的二維半MBB 梁結構成像結果Fig.11 Imaging results of two-dimensional half-MBB beam structure with porous features

5.4 三維結構彈性成像

為進一步驗證本方法的通用性,開展三維結構彈性成像的研究.如圖12 所示的三維懸臂梁結構,結構長為2 m、寬為0.6 m、高為1.2 m,結構左端面施加固定約束,結構被離散為20×6×12 個六面體單元,在結構內部中心位置設置一個尺寸為0.4 m×0.4 m×0.4 m 的損傷區域.分別考慮損傷區域為缺損、結冰、積水三類損傷類型,定義如下3 種存在損傷的三維懸臂梁結構: (1)設置初始無損結構為實體結構,損傷區域為缺損,缺損區域材料彈性模量設置為0.001E0,材料密度設置為0.001ρ0;(2)設置初始無損結構為具有多孔特征的結構,該結構由20×6×12 個多孔單胞構成,結構彈性模量和材料密度分別設置為0.5E0和0.5ρ0,損傷區域為結冰,結冰區域的彈性模量和材料密度分別設置為E0和ρ0;(3)同樣設置初始無損結構為具有多孔特征的結構,該結構也由20×6×12 個多孔單胞構成,結構彈性模量和材料密度也分別設置為0.5E0和0.5ρ0,但損傷區域為積水,由于積水僅影響結構質量,因此積水區域的材料彈性模量不變,材料密度設置為ρ0.本算例在結構上端面與后端面交線長度方向3/4 位置的節點上施加數值大小為結構域質量20%的非結構集中質量.三維結構相較于二維結構的模型更加復雜,逆向反演三維結構的損傷也更為復雜,為了提高損傷識別精度,本三維算例選取的特征值階數比二維算例略多.本算例考慮結構前10 階特征值,每階特征值權重均設置為0.1.

圖12 內置損傷的三維懸臂梁結構Fig.12 Three-dimensional cantilever beam structure with built-in damaged

如圖13 所示,彈性成像迭代曲線光滑且目標函數最終收斂,彈性成像模型經過680 次迭代后得到如圖14 所示的F 缺損結構的成像結果.如圖15 所示,隨著優化的進行,目標函數值下降速度由快到慢并且很快收斂,經過531 次迭代后得到如圖16 所示的F 結冰結構的成像結果.如圖17 所示,彈性成像模型迭代197 步后目標函數開始趨于平穩,經過256 次迭代后得到如圖18 所示的F 積水結構的成像結果.由于損傷位于結構內部導致不方便觀察,因此通過顯示半邊結構空間的成像結果來解決這一問題.從3 個三維結構成像結果圖中可以看出,最終成像結果所呈現的損傷區域位置及大小與設定損傷區域基本一致,表明本方法用于三維結構同樣具有良好的損傷識別效果.雖然三維結構彈性成像問題相較于二維結構彈性成像問題計算成本略高,但是三維成像只需定義新的三維結構無阻尼自由振動系統有限元模型,損傷表征、彈性成像模型和求解算法均與二維成像保持一致.

圖13 內置缺損的三維懸臂梁結構彈性成像迭代曲線Fig.13 Iterative curve of elastography of three-dimensional cantilever beam structure with built-in defect

圖14 內置缺損的三維懸臂梁結構成像結果Fig.14 Imaging results of three-dimensional cantilever beam structure with built-in defect

圖15 內置結冰的三維懸臂梁結構彈性成像迭代曲線Fig.15 Iterative curve of elastography of three-dimensional cantilever beam structure with built-in ice

圖16 內置結冰的三維懸臂梁結構成像結果Fig.16 Imaging results of three-dimensional cantilever beam structure with built-in ice

圖17 內置積水的三維懸臂梁結構彈性成像迭代曲線Fig.17 Iterative curve of elastography of three-dimensional cantilever beam structure with built-in water accumulation

圖18 內置積水的三維懸臂梁結構成像結果Fig.18 Imaging results of three-dimensional cantilever beam structure with built-in water accumulation

6 結論

本文提出了一種考慮剛度和質量耦合效應的結構彈性成像方法,構建了缺損、夾雜、結冰和積水多種損傷類型的統一表征,并構建了損傷表征、力學模型和特征值響應之間的映射關系,建立并求解了結構彈性成像模型.研究結論如下:

(1)本方法可有效識別結構缺損、結冰、積水多種損傷類型的位置、數量和形狀;

(2)結構彈性成像結果不受特定邊界條件限制,無需先驗信息可自動反演單/多個損傷;

(3)本方法在二維和三維結構彈性成像問題中具有通用性.本方法豐富了現有機械結構損傷識別方法的理論內涵,有助于實現重大機械工程裝備的服役安全評價.