構建有效問題鏈 提升數學學習力*
——以“變量與函數”為例

童 佳

? 湖北省武漢市糧道街中學

1 教學立意

課程標準認為,數學學科核心素養主要表現為會用數學的眼光觀察世界,會用數學的思維思考世界,會用數學的語言表達世界.如何在教學中落實好呢?關鍵是要結合相應的教學內容,在落實“四基”“四能”的過程中,促進學生數學學科核心素養的形成與發展.而基于學情設置有效的問題鏈就是一種有效的方法,它激發學習動力,鍛煉毅力,培養創造力,提升學習能力.

下面,以“變量與函數”為例來探討如何構建有效的問題鏈,提升學生數學學習力.

2 教學過程

2.1 創設問題情境,激發學習動力

問題1生活中有許多運動變化的事物,請大家觀察圖1中的兩幅動態圖片,其中分別有哪些變化的量呢?它們是怎么變化的呢?

圖1

問題2你能舉出一些這樣的例子嗎?

設計意圖：創設實際生活中的問題情境,學生初步感受函數的本質,激發學習興趣,提升學習動力.通過問題2,學生感受到生活中存在大量一個變量隨著另一個變量的變化而變化的實例,明確學習函數概念的必要性.

2.2 合作探究,培養毅力與探究力

活動1：十一黃金周期間,小明騎共享單車去黃鶴樓景區,他以0.2 km/min的速度勻速行駛,行駛的路程為skm,行駛的時間為tmin.

問題1請填表1.

表1

問題2速度、路程與時間中,哪些是變量?

問題3這些變量之間有什么關系?可以用一個關系式來描述嗎?

設計意圖：學生經歷填表的過程,初步感受每一個時間t就有一個唯一確定的路程s與之對應.構建有效的“問題鏈”,將問題聚焦在兩個變量之間的關系上,引導學生思考,培養學生的抽象概括能力.

活動2：在景區,小明查詢了近5年十一黃金周期間來武漢游玩的人次(如表2).

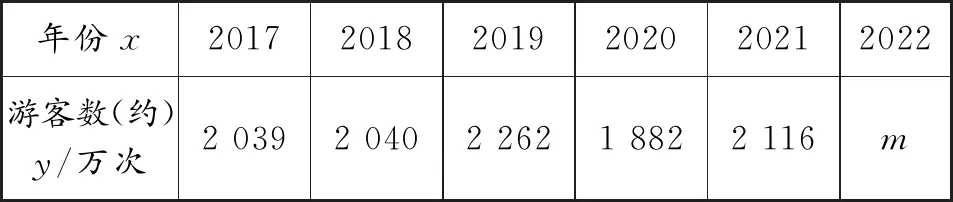
表2

問題1活動2中涉及的量哪些是變量?

問題2這些變量有沒有像上面那樣的關系式呢?它們之間又有什么關系呢?

問題32022年來武漢游玩的人數m是唯一確定的嗎?說說你的理由.

問題4你估計m的值是多少?

設計意圖：通過問題鏈引發學生思考函數概念的本質.m值的估計,不僅加深了學生對“唯一確定”的深刻理解,同時弘揚了偉大的抗疫精神,從而達到數學育人的目的.

活動3：在景區,小明也感受到了十一黃金周期間武漢氣溫的適宜!下面是景區某天的氣溫變化圖,圖2中點的橫軸t(單位:時)表示時間,縱軸T(單位:℃)表示氣溫.

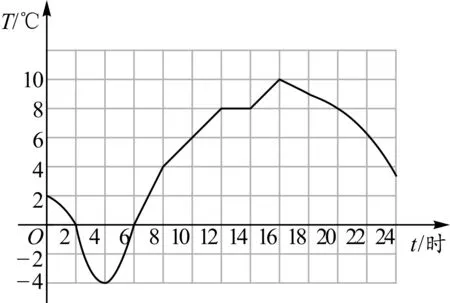
圖2

問題1氣溫變化過程中有幾個變量?

問題2時間t與氣溫T之間又有什么關系呢?你能列出它們之間的關系式嗎?

問題36時的溫度是多少?

問題410時的溫度是多少?22時呢?它們之間有什么關系?

設計意圖：通過學生熟悉的氣溫圖,體會在運動變化中當時間t確定時,氣溫T也隨之確定.同時通過問題鏈,將概念的內涵向縱深發展,體會不同的時間t可能對應相同的氣溫T.

活動4：請認真觀察以上3個活動中相應的運動變化過程.

問題1每個運動變化過程有幾個變量?

問題2在同一運動變化過程中,兩個變量之間是否具有相同的關系?

設計意圖：通過問題鏈,將思考的核心再次聚焦到函數概念的本質上來,培養學生從實例中提煉、歸納事物共性的能力.

2.3 初步辨析概念,提升辨析能力

活動5：辨析.

問題1觀察下列式子,y是x的函數嗎?

(1)y=x-1; (2)y=x2;

問題2問題1的式子中,x是y的函數嗎?

問題3下列圖象中,y不是x的函數的是( ).

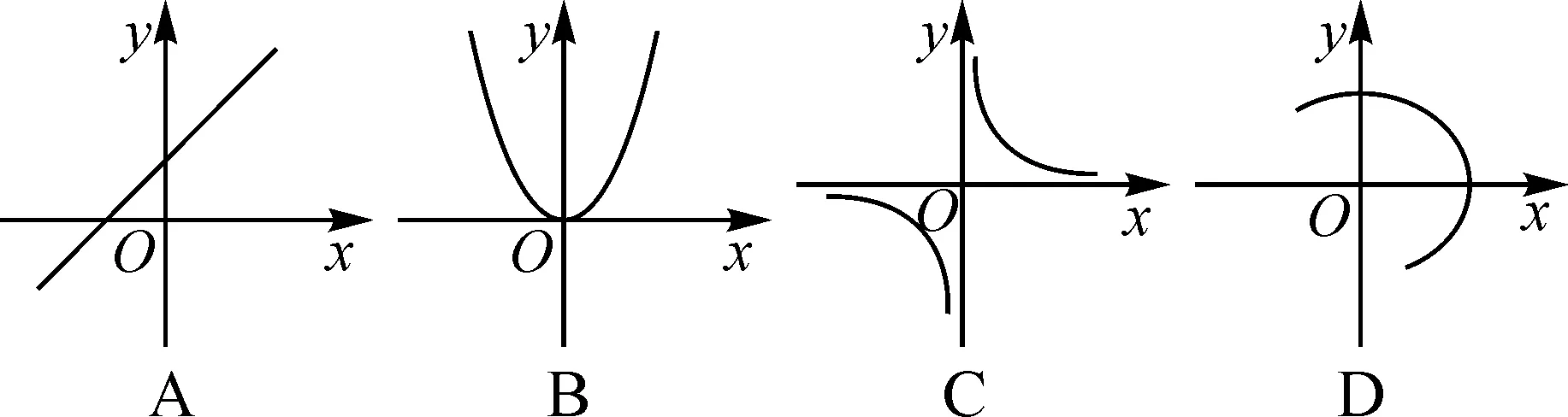
設計意圖：通過上述問題鏈,進一步強化學生對函數概念中“唯一確定”的理解,提升學生的辨析能力.

2.4 綜合應用概念,培養創造力

活動6：一輛汽車的油箱中現有汽油50 L,如果不再加油,那么油箱中的油量y(單位:L)隨行駛路程x(單位:km)的增加而減少,已知汽車平均耗油量為0.1 L/km.

問題1y是x的函數嗎?你能寫出y與x之間的關系式嗎?

問題2汽車行駛100 km,油箱中還有多少油?

問題3當油箱中的油量還剩20 L時,汽車行駛了多少路程?

問題4汽車最多能行駛的路程是多少?

問題5你能指出自變量x的取值范圍嗎?那y呢?

問題6從黃鶴樓景區到武當山風景區約有417 km,當油箱中還有10 L汽油時,汽車的油燈就會報警,該汽車在去武當山風景區的途中會報警嗎?

設計意圖：強化學生對函數概念的理解,引出函數解析式、函數值、最值等概念.問題6引導學生體會數學建模的過程,提升學生分析問題與解決問題的能力.

活動7：請寫出下列問題中y關于x的函數解析式,以及自變量x的取值范圍.

問題1y是x的0.8倍.

問題2某種原價為x元的商品,按8折出售,現售價為y元.

問題3一個矩形相鄰的兩邊長分別為0.8和x,面積為y.

設計意圖：“問題鏈”讓學生明顯地意識到同一個函數表達式可以表示不同的意義.同時,強調在求自變量x的取值范圍時,需注意它的實際意義.

2.5 歸納概念,培養表達能力

問題1這節課你學習了哪些新的數學概念?

問題2你能用幾個關鍵詞概括一下今天所學的內容嗎?

問題3如果繼續研究函數,將研究哪些內容呢?從什么方向上去研究呢?

設計意圖：通過問題鏈,引導學生提煉本節課所學的數學知識與思想方法,強化“唯一確定”.同時,引導學生發現問題,提出問題,體會函數單元的整體性.

2.6 布置作業(略)

3 教學反思

本節課通過構建有效的問題鏈,引導學生體會函數概念學習的必要性,函數概念生成的自然性,函數概念理解的深刻性,以及函數概念應用的廣泛性,激發學生學習動力,培養學生毅力,提升學生探究能力、辨析能力、創造能力等數學學習力.而就如何設計有效的問題鏈接這一點,筆者有如下三點思考:

(1)問題鏈的構建要有關聯性.借用小明去黃鶴樓發生的3件事,構建了3組各問之間都有連接的問題鏈.學生分別從解析式、表格、圖象中尋找兩個變量之間的本質關系,形成函數概念.

(2)問題鏈的構建要有生長性.在構建問題鏈時,臺階跨度要合適,要有梯度和生長性.活動6,讓學生的思維呈螺旋式上升,特別是第6個問題,無形中滲透了數學建模、函數與方程,以及多角度分析問題的數學思想方法.

(3)問題鏈的構建要能激發學生思維碰撞的火花.為有效突出重點、化解難點,應結合相關的內容與學情,圍繞函數概念的本質上構建問題鏈.活動2與活動3中的問題2都是為幫助學生破解函數不一定都要有明顯的解析式而僅需“唯一確定”,不同的自變量對應的函數值可以相同等難點.Z