對初中數學整體性教學的幾點認識
印海梅
? 江蘇省南通市海安市雅周鎮初級中學
數學知識不是孤立存在的,它們之間存在著千絲萬縷的聯系,這就要求在教學中不能孤立地看問題,應善于從整體出發,從宏觀的角度去思考問題,從而幫助學生建構完善的認知體系,提升學生知識遷移能力[1].在實際教學中,為了教與學的需要,教師常常將這些相關聯的內容分割開來,以此降低知識難度,讓學生更好地理解知識、掌握知識.不過,這樣的分割和細化有其優勢,但也存在著一些不足.因為這樣學生所獲得的是一個個“點狀”的知識,不利于知識的系統化建構,影響知識的遷移.基于此,在教學中.教師有必要對教學內容進行高效整合,以整體的方式來教學,以此將點連成線,編織成網,提高學生信息提取能力、知識遷移能力,提升教學效率.
筆者結合一些具體教學實踐活動,分析了整體性教學的價值,供參考!
1 以知識的系統化建構為目標開展章起始課
章節起始課主要告訴我們“學什么”和“怎么學”的問題,其在教學中往往起承上啟下的作用.在章起始課教學中要引導學生建立知識框架,幫助學生初步建立對本章內容的整體認識,同時也要進行學習方法的滲透,充分發揮先行組織者的作用.在起始課中,教師要嘗試激活學生已有的認知,凸顯新知與舊知之間的聯系,化陌生為熟悉,提升學生數學學習學習興趣;又或者在起始課提供一個框架和線索,形成“導學圖”,讓學生明晰研究方向,了解研究方法,提升教學有效性[2].不過,在實際教學中,這部分內容并沒有引起師生的足夠重視,他們往往僅視其為閱讀資料,沒有進行認真的分析和提煉,從而影響了整體知識框架的建構.要知道,只有了解整體知識框架,才能更加系統和全面地認識本章內容,從而在學習過程中做到“形散而神不散”.
案例1“一元二次方程”起始課
師:看到課題,你想到了之前學習的哪些內容呢?
生齊聲答:一元一次方程,二元一次方程(組),三元一次方程(組).
師:它們的概念是什么?(答略.)
師:這些方程(組)的解分別有幾個?是如何求解的?
借助問題喚醒學生的已有認知,為新知的學習搭建知識框架,同時通過類比促使學生得到一元二次方程的概念,掌握本章內容的研究思路.
通過以上問題,幫助學生建構知識框架(如表1).
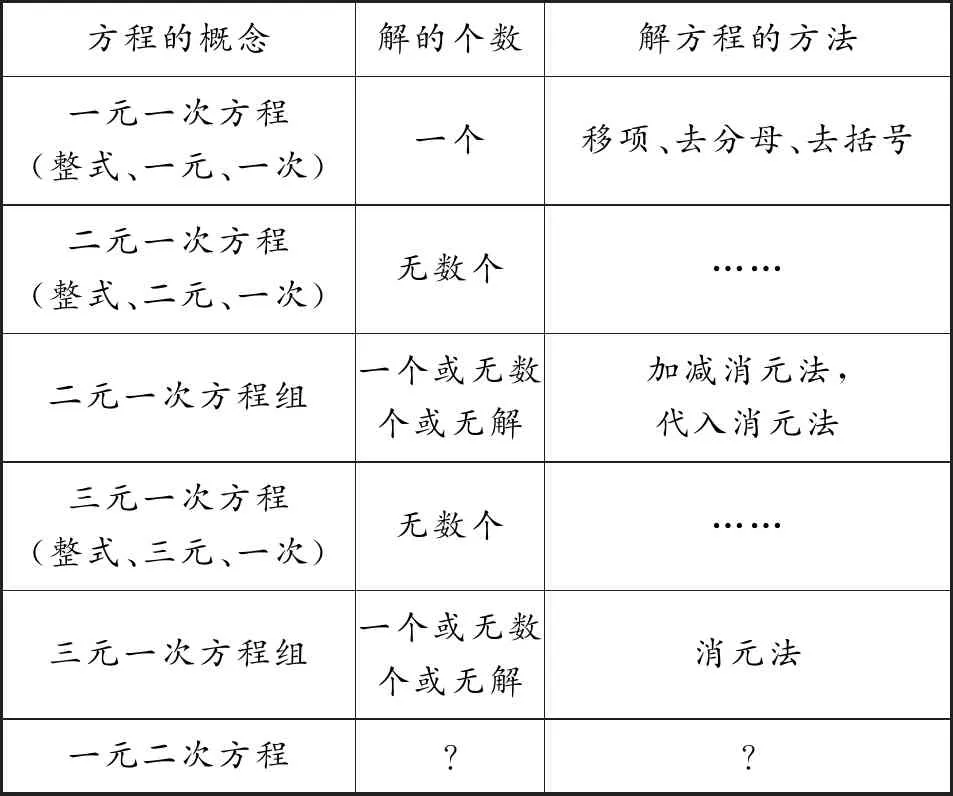
表1
師:類比以前所學方程的定義,你能為一元二次方程下定義嗎?
師:你能列舉幾個具體的例子嗎?
設計意圖:本章內容與之前所學的方程內容息息相關,這樣與舊知相類比可以讓學生站在整個方程體系的角度上思考問題,理解新知.通過類比不僅幫助學生鞏固了已學知識,而且有利于學生將新知納入到已有的認知體系中去,從而逐漸完善知識體系.同時,舊知的回顧為新知的探究指明了研究思路,使得學生學起來更加輕松,有助于提升學生自主學習意識,激發學生數學學習興趣.
2 以深化知識理解為目標開展知識類比課
類比教學是數學教學的重要手段之一,其有助于知識的深化與認知體系的建構.在教學中通過對相似屬性或相關結構的類比,可以激發學生潛能,培養學生創新意識.數學知識往往都存在著并列結合的關系,在教學中適當地運用類比,有助于知識的內化,有助于教學效率的提升.
案例2“一元一次不等式”第一課時
環節1:創設情境,類比概念.
創設情境:某電梯的荷載為1 000 kg,電梯內有一個體重為40 kg的小孩和若干大人(大人的平均體重為60 kg),若要保證電梯正常運行,電梯最多可以乘坐幾個大人?
設計意圖:借助生活情境引出40+60x≤1 000和40+60x=1 000兩個式子,通過觀察、類比,總結歸納出一元一次不等式的概念,并通過與方程解的類比,讓學生明晰不等式的解需要用不等式來表示,從而逐漸抽象出不等式解的概念.
環節2:合作探究,類比性質.
師:說一說,下列式子哪些是不等式?并求出不等式的解.(教師PPT給出題目.)
①1+x>4; ②3x<5; ③1+7x>5x-3.
通過前面的對比分析,結合學生的已有經驗,學生會憑直覺自動地進行移項、化“1”等操作.為了讓學生進一步理解其背后的道理,可以通過提問的方式引發學生思考、總結、歸納,得到不等式的基本性質.“不等式兩邊乘(或除以)同一個負數時不等號要變號”的問題一直是教學的重難點,教師可以組織學生進行合作探究,通過探索、交流來突破教學重難點.
師:解不等式-2x<6.
從學生的反饋來看,有的學生的答案為x<-3,有的答案為x>-3,由此引發認知沖突.此時,鼓勵學生去討論、驗證、發現,由此總結歸納出當不等式兩邊乘(或除以)同一個負數時不等號需要變號的結論.這樣經歷自我發現的過程,不僅深化了學生對不等式基本性質的理解,而且突出了不等式的基本性質和等式的基本性質的差異性.
設計意圖:初中生已具備一定的自主學習能力,為此在教學中多鼓勵學生進行合作探究,培養學生的問題意識,提高學生自主解決問題的能力.在探究活動中,組織學生將一元一次不等式與一元一次方程的概念、性質、解法相類比,最終形成了這一章的知識框架,凸顯知識間的區別與聯系.
3 以發展學生為目標開展教材整合課
數學教材是專家精心編寫的,具有廣泛的普適性,但是因教學環境、學生知識背景等諸多因素的影響,在教學中仍然有必要對教材內容進行整合,使其轉化為適合學生發展的教學內容.對于整體性教學來講,首先要有打破常規的勇氣,要善于根據教學實際將“教材編排”“課時安排”等內容重新規劃和整合,使教學內容更適合本班學情,更適合拓寬學生的思維,以此激發學生智慧,提升教學效率[3].
案例3兩個三角形相似的判定
課前整合:本教學班學生的基礎較好,適應能力強,加之“相似三角形判定的預備定理”與前一節例題的證明思路有著明顯的關聯性,為此將教學內容前置,把對“相似三角形判定的預備定理”的探究作為前一節課的變式題,并加以證明.
課中整合:傳統課堂在教學“兩個三角形相似的判定”時會分為三個課時完成,每節課講解一個定理,然后安排相應的練習.整合后,同樣按照三個課時完成.第一課時,將三個判定定理整合在一節課完成,然后配備一些基礎題進行相應的練習,以便于學生掌握三個判定定理.第二課時,安排一些難度略高的題目,讓學生靈活運用相關判定定理解決問題,以此實現知識的深化.第三課時,開展作業評講課,教師基于學生練習反饋,總結學生學習中存在的認知漏缺,以此通過針對性的引導實現知識的內化.
設計意圖:從整體角度分析發現,“相似三角形判定的預備定理”與前一節課的例題具有明顯的關聯性,只要將例題中的中點條件弱化改為平行即可完成證明,為此可以對教材內容進行適當的調整,這樣既體現了知識的連貫性,又為后面整合教學提供了時間保障.另外,在傳統教學中將三個判定定理分開講授,這樣學生的“學”可能就會止步于簡單的動手操作和簡單的判定運用,而且在解題時容易出現機械的模仿和套用,不利于對知識的整體認識.仔細分析不難發現,三個判定定理的證明具有高度的一致性,并且它們的推導過程是逐層提升的,呈現一定的邏輯性,前面的推導為后面的推導作了思維鋪墊.這樣將它們整合在一起,表面上看容量較大、難度較高,但若發現其中的關聯后,不僅可以降低思維的難度,而且通過對比分析可以讓學生理解和掌握數學的研究方法.另外,整合后,課堂上可以有更多的時間進行拔高訓練,有助于提高學生解題能力.可見,有效的整合為學生提供了更為廣闊的探究空間,有助于學生知識、思維、智慧的全面提升.
總之,教師要善于從整體出發,在基于“三個理解”的基礎上合理地建構,讓學生可以更好地理解知識、應用知識,提高教學有效性.

