數(shù)學高階思維的生本課堂演進

張娟萍

? 浙江省杭州市臨安區(qū)青云初級中學

培養(yǎng)學生數(shù)學高階思維的重點是課堂中使學生深度卷入數(shù)學活動過程,實現(xiàn)思維進階.課堂中踐行“不用PPT,不用現(xiàn)成的數(shù)學題”[1],由學生生成數(shù)學任務、生長數(shù)學知識,親歷數(shù)學知識的發(fā)生、發(fā)展過程.課堂中的練習題由學生根據(jù)習得的數(shù)學知識自己編制而成,讓學生親歷提出問題、分析問題與解決問題的過程.課堂以學生主動參與為本,以深度經(jīng)歷和體驗為徑,以思維層次的提升為旨.下面以“特殊平行四邊形”[2]單元復習課為例,談談“生本、生成、生長”的課堂演進過程.

1 由學生梳理知識,架構體系

問題1你有哪些辦法判定一個四邊形是平行四邊形?

學生回顧之前學過的知識,通過思考,回答平行四邊形的判定方法,教材提供了三個判定定理.

問題2能否說出所有判定平行四邊形的方法?

這個問題其實就是指向于學生去尋找判定方法的規(guī)律或者基本特征,追蹤“判定”的基本方法.

學生面臨任務時,會產生思維的沖突.首先激發(fā)獨立思考,產生想法,需要得到其他同學共鳴;碰到困惑和挫折,需要得到其他同學提示和啟發(fā).這樣學生就會產生交流需求,自覺進入群組互動環(huán)節(jié).

群組互動:讓組內每位學生“出聲思考”——“說出”自己的思維及其發(fā)現(xiàn)過程,實現(xiàn)思維曝光.

小組反饋:要判定一個四邊形是平行四邊形需要兩個特征條件,可以考慮邊的特征,也可以考慮角或者對角線的特征,梳理得到平行四邊形有十個表現(xiàn)特征,分別為兩組對邊相等、兩組對邊平行,兩組對角相等,兩組鄰角互補,兩條對角線互相平分.這十個特征里任選兩個作為條件就可以得到四十五種判定平行四邊形的方法,如表1.至于這些判斷方法是否正確,有待驗證.如果是真命題,則需要證明;如果是假命題,則需要舉出反例.

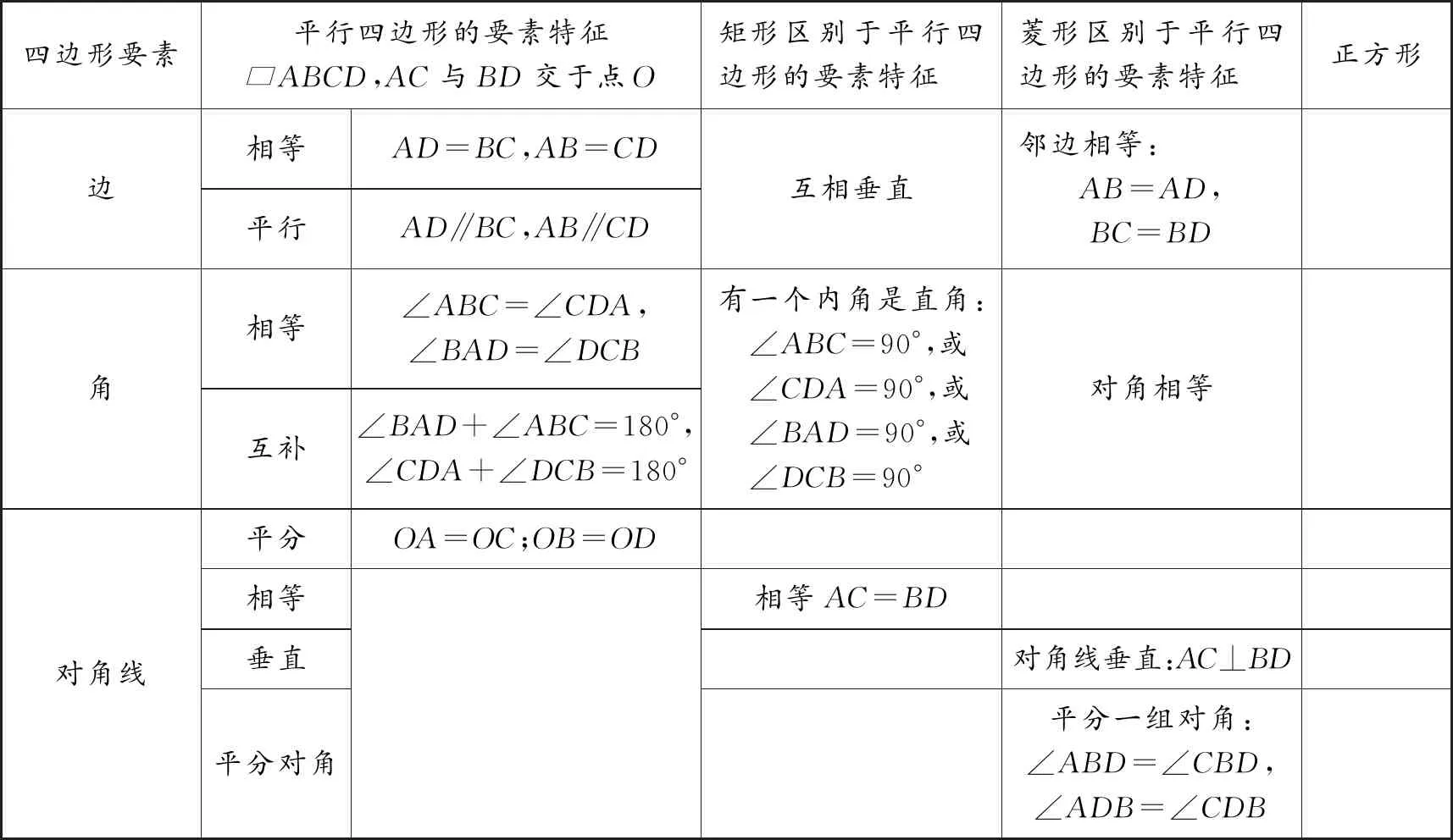
表1

問題3可以用這種方式類比探究其他圖形嗎?

學生自主探究:獨立思考—群組互動—反饋.要判定四邊形是矩形,還需增加一個矩形的特征.矩形有兩個表現(xiàn)特征,選其中一個,即可在原來判定平行四邊形的基礎上判定矩形.同樣的道理要判定四邊形是菱形,還需增加一個菱形的特征,菱形有三個表現(xiàn)特征,選其中一個,即可在原來判定平行四邊形的基礎上判定菱形.同學們得到45×2×3=270種判定一個四邊形是正方形的方法.因而非常激動,由同學歸納判斷一個四邊形是平行四邊形的基本策略,如圖1所示:

圖1

這其實是方法的習得,不僅可以重新梳理整合之前學習過的圖形的判定方法,還可以用這樣的方法探究新的圖形.

2 由學生編題,將知識轉化為問題解決

任務:既然學習了判定一個四邊形是平行四邊形方法,那么用這些知識可以解決什么樣的問題呢?

此問題引起學生思考如何將知識轉化為數(shù)學題,養(yǎng)成數(shù)學知識的應用意識.

環(huán)節(jié)1：每個學生獨立編題.

環(huán)節(jié)2：學生編題后小組交流,保證編的題更有科學性和針對性.通過互動,學生的思維能得到回應和反饋.吸收各小組反饋的不同結論、不同思考路徑和創(chuàng)造性的想法,并對自己的思維進行進一步加工,因此,群組交流的過程是思維的優(yōu)化過程.

環(huán)節(jié)3：每一組反饋所編的不同類型的題.

環(huán)節(jié)4：組際交流.將各組反饋的所編題目按不同類型、不同難度進行歸類和排序,使解決問題變得有序而有梯度.

環(huán)節(jié)5：呈現(xiàn)最終分類、分層的學生編題.本節(jié)課組際評估出的思維水平層次較高的兩道編題如下:

例1如圖2,在△ABC中,AB=AC,AD⊥BC,垂足為D,AN是△ABC外角∠CAM的平分線,CE⊥AN,垂足為E.

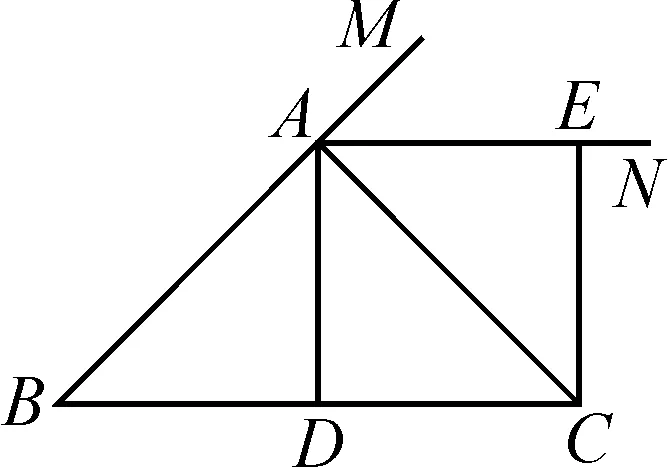
圖2

(1)求證:四邊形ADCE為矩形;

(2)添加什么條件時,四邊形ADCE是一個正方形?

例2已知,兩個含30°角的三角板ABC和FED如圖3-1放置,現(xiàn)翻折三角板FED到FE′D,如圖3-2)所示.

圖3-1

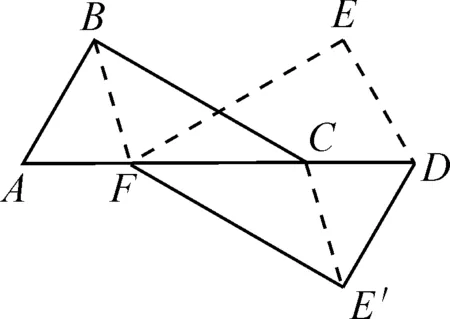
圖3-2

(1)求證:四邊形BFE′C是平行四邊形.

(2)要使四邊形BFE′C是矩形,還需要什么條件?有沒有辦法使它為正方形?

3 由學生追蹤解題和編題過程,提煉方法

環(huán)節(jié)6：解決問題,質疑、拓展.

(1)要求所有學生將他組編的題,落到筆頭.

(2)反饋不同解法、思路及其發(fā)現(xiàn)的路徑;反饋遇到的挫折及其解決辦法;反饋存在的疑問或質疑;反饋有創(chuàng)造性的想法,包括有創(chuàng)造性但沒有形成結論的想法、有創(chuàng)造性但結論錯誤的想法;反饋可能碰到的典型錯誤.

(3)由學生對編題和解法提出質疑和變式.

(4)教師隆重地板書,記錄學生的表達.

各組在互相點評、反饋的過程中,吸收并優(yōu)化了自己的思維．

環(huán)節(jié)7：展示編題路徑、提煉編題方法.以供沒有編出題目或者不是按這樣的思路編題的同學學習、反思和評估.

編得例1的同學反饋:要編一個矩形判斷的問題,可由平行四邊形加一個直角的條件得到,而平行四邊形可以由兩組對邊分別平行得到.其中一組對邊平行由“角平分線+等腰三角形”得到;另一組對邊平行和直角,由“垂直于平行線的兩直線”得到,如圖4所示.

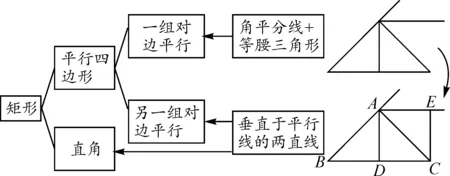
圖4

編得例2的同學反饋:如圖5所示的流程,我們組想要用一種對邊平行且相等來得到一個四邊形是平行四邊形,而對邊相等可以由全等得到,我們每個人手頭上都有兩副三角板(用同是含30°角的直角三角板),如圖3-1,兩條斜邊一部分重疊在一條直線上,就滿足了第一個條件.然后,想要用內錯角相等來得到對邊平行,這里有內錯角,但是沒能得到平行線的內錯角,于是把一個三角板翻折下去,如圖3-2,只要判斷四邊形BFE′C是平行四邊形即可.

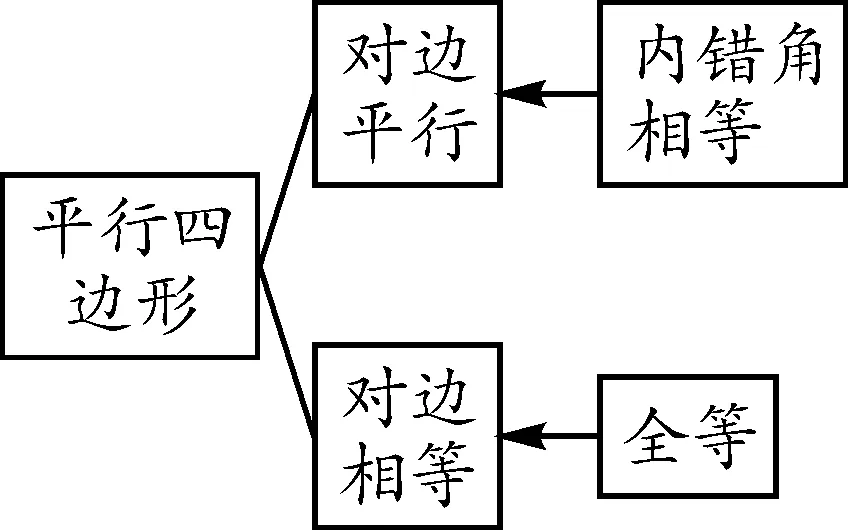
圖5

評析：這個環(huán)節(jié)最有創(chuàng)造性的表現(xiàn)是將三角板實物操作過程“翻譯”成數(shù)學圖形,補全△DE′F,尤其補全在實物操作中并不存在的兩條線段BF和E′C是題目編成和實際問題數(shù)學化的關鍵所在,“畫出圖形”需要學生正真理解問題的本質.

接著,按照圖形特征研究的一般方法,想到在平行四邊形的基礎上,需要添加什么條件得到一個矩形呢?我們在平行四邊形BFE′C的∠FBC處添加了一個直角符號,但圖中∠FBC明顯不是一個直角,所以不能直接畫一個直角符號就表示它是直角了.先把平行四邊形畫成矩形,判斷它還需要補充什么條件.

評析：從圖3-2到圖6-1,對學生來說是一個非常簡單的嘗試,但對下一步起到了重大的作用.因為緊接著他們要補充條件得到一個正方形.

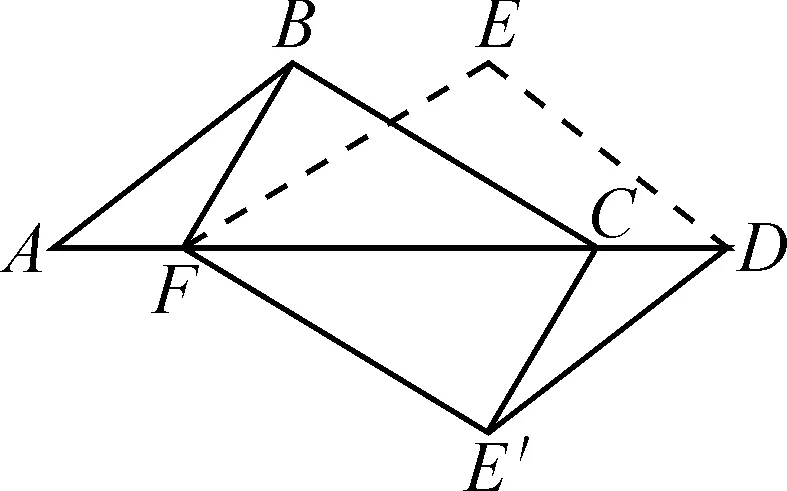
圖6-1

根據(jù)剛才的思路,先把這個正方形畫出來,滿足正方形的特征,正方形的對角線平分一組對角(還需滿足FB與FE′對稱),而根據(jù)操作,FE′是由FE翻折得到的,因此,當平行四邊形BFE′C是正方形時,FB與FE重合,所以點B與E重合,得到圖6-2.

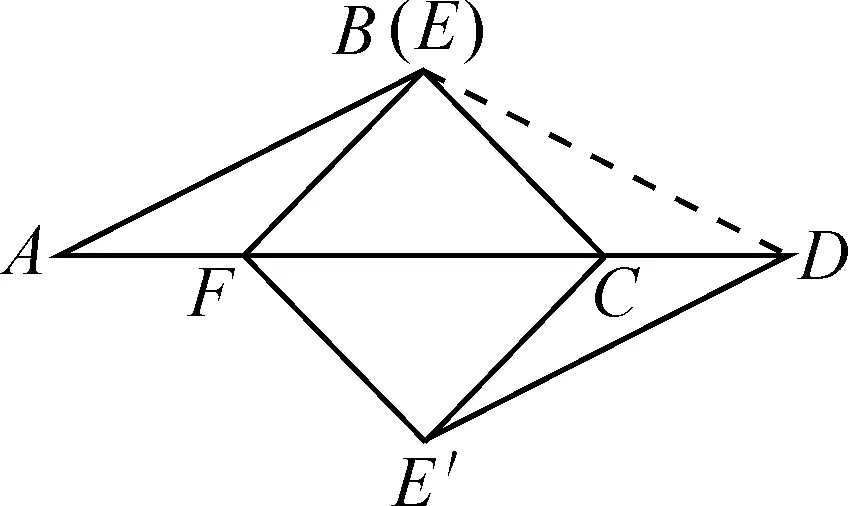
圖6-2

從圖6-1到圖6-2,是學生創(chuàng)造性思維的體現(xiàn),它來自于數(shù)學知識和數(shù)學學習本身的邏輯.最后創(chuàng)造性得到綜合問題:△ABC沿AC的一條垂線對稱得到△DEF(如圖3-1),再沿AD所在直線對稱到△DE′F(如圖3-2).(1)求證:四邊形BFE′C為平行四邊形.(2)再添一個什么條件可得到矩形、正方形呢?學生經(jīng)過作圖得到圖6-2,從而確定題目條件．

學生編的題完全達到了本堂課所要求的思維水平層次,給學生帶來了很大的鼓舞、震撼和觸動.

組際提出質疑:三角板按圖3-1放置,本身是一個對稱圖形,平移就可以直接得到平行四邊形,那么他們組通過翻折得到圖3-2,想得到平行四邊形考慮再對稱,兩次軸對稱就成了一次中心對稱,直接得到平行四邊形.

評析：整個構圖過程中,學生自己嘗試條件的構造,經(jīng)歷了由知識點到圖形符號到數(shù)學問題的構造過程,學生的評價和質疑促進學生從不同角度進行思考,對問題的本質有了更深層次的理解.

環(huán)節(jié)8：評價解題和編題.(1)自我評估.有什么思維的增長?有什么方法、能力的提升?(2)群組學生評價和質疑.小組以題目原創(chuàng)、新穎、思維含量高、解法多樣、編題方法可操作等為評價標準.(3)教師評價.以學生為主體的課堂中,學生思維的深度在于群組互動時,教師能否敏銳地抓取到學生生成的創(chuàng)造性信息及不同的思維路徑.教師要大張旗鼓地鼓勵學生表達群組互動中產生的質疑、有創(chuàng)造性的想法.這是對學生創(chuàng)造性思維的一種肯定,倡導學生不只是追求正確的結論,更多地去追求創(chuàng)造性思維過程.

評析：由學生編題,使問題產生(編題及方法)與問題解決(解題及方法)形成閉環(huán),小組交流、反饋,促成學生創(chuàng)造性思維,提煉編題的方法.教師的行為、煽動性的追問,是鼓勵和回應學生的創(chuàng)造性思維和方法的重要策略.

4 生本課堂發(fā)展學生高階思維的關鍵

促動學生高階思維的課堂,關鍵在于能否以學生為主體.這需要解決以下三個問題:

(1)學生編出來的問題不是教師想要的問題怎么辦?學生之所以編出這些問題,是他認知范圍內知識產生的路徑所理解的問題表述.不用PPT的好處就是可以把這些問題納入課堂要解決的問題,如果預設PPT的話,那么學生編出來的問題不在PPT預設之內,就會經(jīng)常出現(xiàn)這樣的狀況:你這個問題很好,我們課后去研究.因此,利用PPT會造成教學沒有辦法以學生為中心.至于這個問題的科學性和內容的針對性在小組互動的時候,已經(jīng)篩選過了,并進行了分類、分層.因此,凡是學生編出來的問題都是課堂中要解決的問題,學生編出的問題反應了學生的疑問和當前的認知水平,這些題可能教師自己沒有想到,因而把學生的問題納入到課堂中來,同時,教師的教學策略也應據(jù)此作出改變.

(2)課程內容所涉及到的數(shù)學知識,如果學生編寫的問題中沒有得到反映和完善怎么辦呢?事實上,促動學生有序思考,類比已有知識探究的方法,課堂上所要研究的問題基本上學生都會涉及到;如果沒有想到,小組同學互動一下,經(jīng)過思維的碰撞就會得到這些問題;進一步教師在巡視時可以介入到小組中對類似的探究進行追問,必然會追蹤到問題的本源.

(3)學生為主體的開放課堂怎樣收回來呢?實際上每次上課都要做好整個內容的設計以及PPT(包括PPT的每一張動畫),然后,上課之前經(jīng)過深思熟慮會把PPT刪去,之所以能夠把課堂收回來,最主要的原因是教師對課堂內容非常嫻熟.教師課堂上要關注教學內容和學生的反應,在數(shù)學內容非常熟練的情況下,教師的注意力可都放在學生身上.學生編出來的問題,如果正好是預設體系里有的內容,便可以直接把這個問題納入到本節(jié)教學體系中;如果原預設中沒有,那就是學生現(xiàn)場生成的創(chuàng)造性產物.教師要對學生新生成的問題作出判斷和評估,也就是說,能不能挖取到學生原創(chuàng)的東西,是對教師最基本能力的考量.