單元整體教學中大概念“錨點”價值的分析與應用
——以“長方形和正方形的面積計算”課時為例

蘇州大學附屬吳江學校 （215006） 顧 健

淮陰師范學院 （223300） 任建波

按照整體論的觀點，學習應該被視為一個具有內在生成性的自然整體，這意味著學習應該是以整體的方式進行，而不是分而習之。大概念統攝的單元整體教學設計為學生開展“整體的方式”學習提供了可能。開展大概念統攝的單元整體教學，首先需要對單元進行整體教學分析，既包括解讀教材、提煉大概念，又包括研究學生、分析學生學習起點，在此基礎上，依據大概念的中心性、可持久性、網絡狀和可遷移性等特征，將大概念的“錨點”價值充分彰顯，并滲透和應用到學習活動的聯結、過渡和建構之中。本文以蘇教版教材三年級下冊第六單元“長方形和正方形的面積計算”一課為例，在分析單元整體教學中大概念“錨點”價值的基礎上，對課時教學進行實踐探索。

一、單元整體教學分析

1.解讀教材、提煉大概念

本單元是平面圖形面積計算的起步，從一維的度量轉到二維的度量，起著承上啟下的作用。從知識脈絡上看（如圖1），知識點在教材上呈線性排列，將面積單位的教學分為兩段，中間穿插面積計算，這是因為面積單位之間的進率很難從面積單位本身得出，借助正方形面積更容易理解。教材的編排關注了單元結構，但是前后知識和方法的關聯略顯不足，比如，長度、角、體積的度量本質都是單位個數的累積，如果不將其置于更大的視野中，學生難以形成“度量”的上位概念并搭建整體遷移的支架。

圖1 教材內容分析

基于以上分析，結合《義務教育數學課程標準（2022 年版）》對相關內容的要求，可提煉出本單元的大概念：面積是“數”單位面積的個數，圖形面積具有可加性。在前后知識的相融互通中理解面積，增強幾何直觀和推理意識等。

2.研究學生、分析學習起點

選取本校三年級5個班學生（共196名）進行前測，測試內容和相關結果如下。

前測題1.觀察下面的生活現象（如圖2、圖3），用筆涂一涂、畫一畫或寫一寫，表示它們的不同。

圖2 粉刷墻面

圖3 柵欄圍地

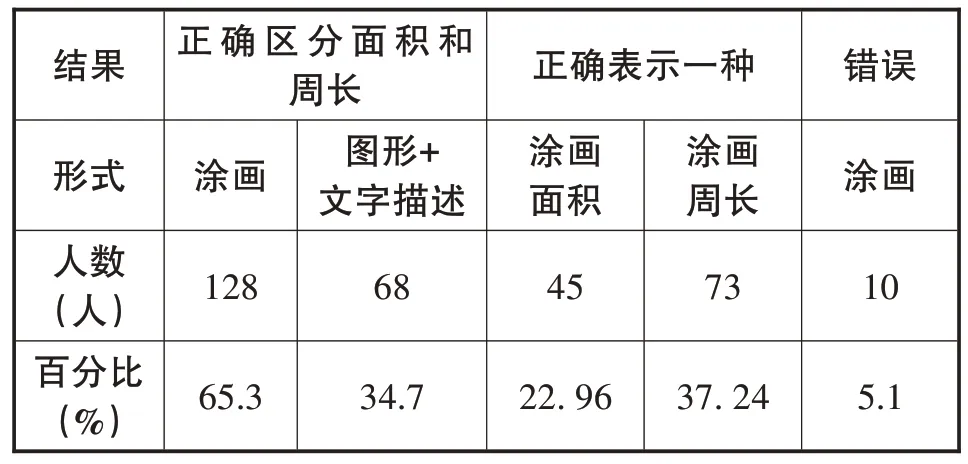
表1 前測題1的測試結果

【分析】從統計結果來看，能識別“面積”的學生占比高達65.3%，這主要有兩個原因：一是生活中有接觸，如“我的手掌比你的大”“我家電視機屏幕比教室里一體機的小”，學生的表達體現了對“面積”的初步感知；二是教材中的滲透，如一年級下冊“認識圖形”單元習題“在正方形、長方形、三角形和圓里分別涂不同的顏色”已經孕伏“面積”的意義。

前測題2.圖4 中的小正方形表示1 平方厘米，①②長方形的面積分別是多少？

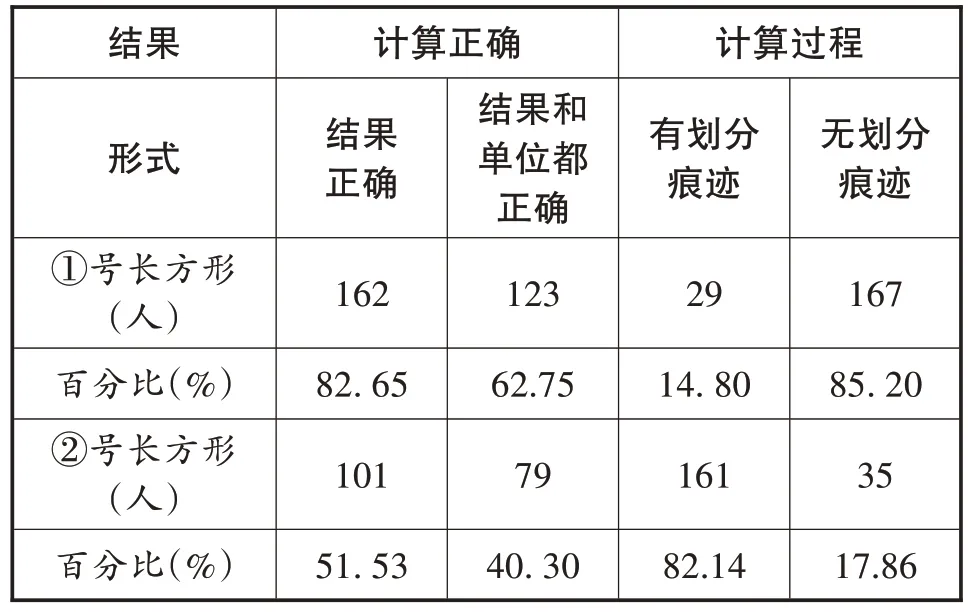
表2 前測題2的測試結果

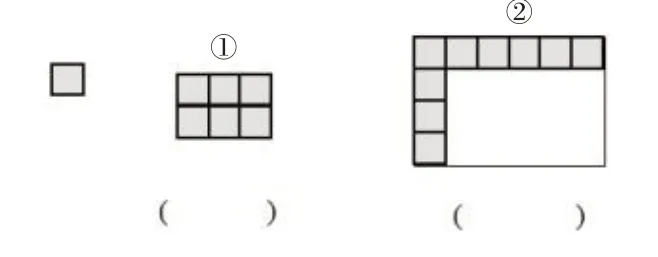
圖4

【分析】統計結果表明，學生借助單位面積用“全覆蓋”方式求①號長方形的面積的正確率達82.65%，而利用“沿邊擺放”方法求②號長方形的面積的正確率只有51.53%，說明學生自主探究有一定的困難。進一步分析，有82.14%都采用了劃分單位面積的方法，說明教師要關注這一年齡階段學生直觀想象和推理能力的培養。

前測題3.你會計算圖5 中長方形的面積嗎？請列式并說明理由。

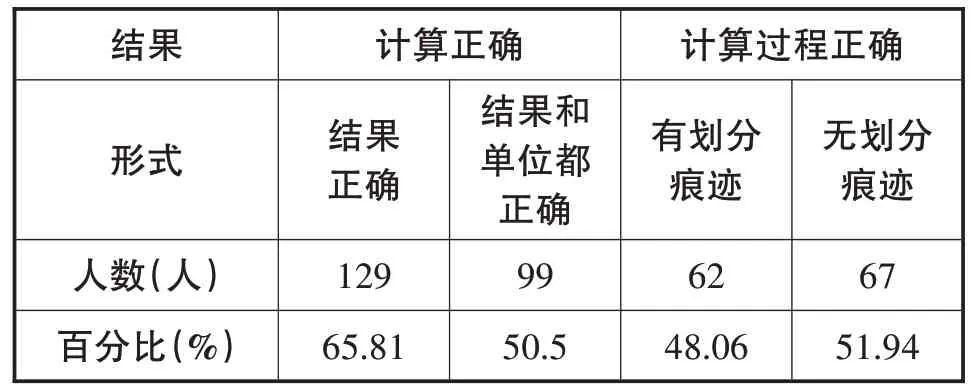
表3 前測題3的測試結果

圖5

【分析】從數據上看，一旦沒有“單位面積”輔助思考，學生的計算正確率驟然下降，只有65.81%，其中，計算正確的學生中有48.06%對長方形進行了劃分。雖然前測題2 已有暗示，但是學生并不能建立單位面積的個數與長、寬數值之間的聯系。這說明教學中要重視長方形面積計算的推導過程，引導學生感悟長度、周長、面積等度量方法的內在一致性。

不難發現，很多學生已經知道了長方形的面積計算方法，但是對“面積大小和計算”的認識仍然浮于表面，難以遷移和感受度量方法的一致性。教學中要著重引導學生經歷用面積單位度量長方形的過程，關聯線段的“測量屬性”，進而推導出長方形和正方形的面積計算公式，為學生后續學習角、圓的面積、長方體的體積做鋪墊。

二、教學活動實踐

［片段1］關聯舊知，激疑啟思

師：還記得怎樣測量線段的長度嗎？（出示圖6）請說一說測量的過程。

圖6

生1：用1 厘米的線段去量，4 個1 厘米就是4厘米。

師：線段長幾個1 厘米就是幾厘米。如果想知道圖7中圖形的面積大小，首先要知道什么？

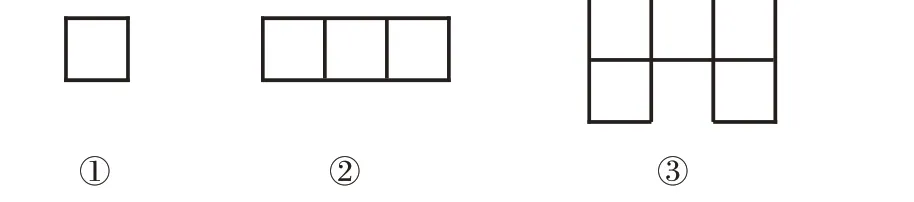
圖7

生2：知道一個小正方形的面積是多少。

師：如果一個小正方的面積是1平方厘米，圖7中圖形的面積分別是多少？

生3：分別是1 平方厘米、3 平方厘米、5 平方厘米。

師：你是怎么想的？

生3：每個圖形中有多少個面積是1 平方厘米的小正方形，面積就是多少平方厘米。

［設計意圖］通過對測量線段長度方法的回顧，使得學生的度量經驗自然遷移到面積測量之中，學生初步建立“單位測量屬性”的知識錨點。在判斷圖7②、③圖形面積時，學生還發現，雖然形狀不同，但是都與小正方形的個數有關，由此感知面積的可度量屬性。

［片段2］實驗操作，探究規律

師：利用1 平方厘米的透明方格紙，拼出一個長方形，并記錄在學習單上（見表4）。

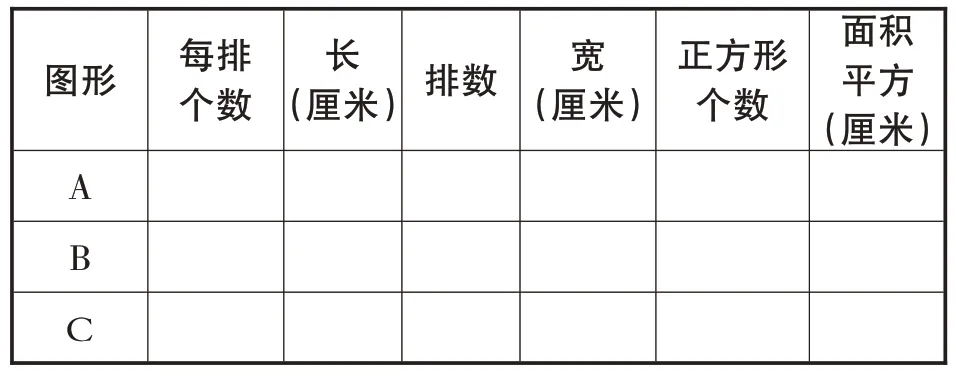
表4 學習記錄單

師：觀察表格，說一說你的發現。

生1：我擺的長方形有4 排，每排有5 個，一共有20個1平方厘米的小正方形，這個長方形的面積是20平方厘米。

生2：我發現長方形的面積與小正方形的個數相同。

師（出示圖8）：根據同學們的發現，可以用這樣的方式表示它們的關系。

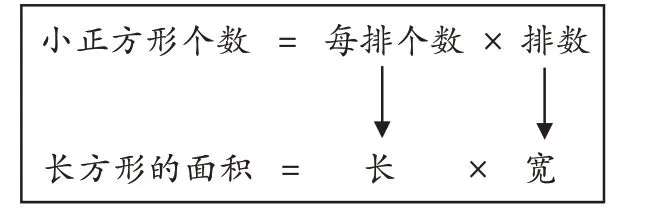
圖8

［設計意圖］學習單給出了思考和觀察的路徑，讓探索有方向。學生在操作中感受到長方形的面積與小正方形（單位面積）個數之間的關系，學習單為聚焦面積概念的本質提供了豐富的表象；通過觀察、說理，學生發現了每排個數與長之間的聯系、排數與寬之間的聯系；通過推理，學生驗證了長方形的面積與單位面積個數之間的關系。雖然從前測的結果來看，“算”更接近學生的思維實際，但是很多學生對面積的理解還是停留在了數值上的相等。

［片段3］抽象推理，得出模型

師（出示長為4 厘米，寬為3 厘米的長方形圖片，圖略）：根據剛才的結論，測量出這個長方形的面積至少需要多少個面積為1 平方厘米的小正方形？

生1：不用鋪滿，只需要沿著它的長擺4 個，沿著它的寬擺3個，一共需要6個小正方形，長方形的面積是4×3=12（平方厘米）。

生2：如果不怕麻煩，只需要一個小正方形，一邊鋪一邊畫線，同樣能算出長方形的面積是12 平方厘米。

師：如果沒有小正方形，怎么能知道這個長方形的面積？

生3：可以用尺子量一量，長是4 厘米，寬是3厘米，4×3=12（平方厘米）。也就是每行可以畫出4個1厘米的小正方形，一共有3排。

師（出示圖9）：回顧剛才的學習過程，從最初的鋪滿，到鋪一部分，到邊鋪邊畫，最后直接量出長和寬，計算出長方形的面積，我們推導出的長方形的面積計算方法是什么？

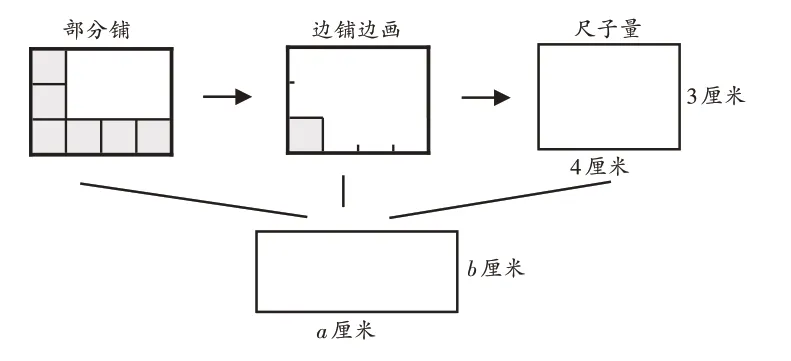
圖9

生4：長方形的面積=長×寬。

師：如果長方形的長用字母a表示，寬用字母b表示，長方形的面積計算可以用字母表示為S=a×b。

［設計意圖］這一環節把密鋪和測量聯系在一起，學生在“操作—想象—符號表征”的過程中能夠提高數學思維力。在進行“部分鋪”的操作中，學生感知了長方形的面積與長、寬相關；在“邊鋪邊畫”的想象中，學生明確了二維圖形的面積需要兩個一維線段長度的數值進行刻畫；在總結計算公式可用符號表征的推理中，學生經歷從“特殊”到“一般”，體會符號表征的簡潔性。在整個過程中，學生理解了面積的內涵，實現了從操作的“實踐表征”向“空間想象”的邁進。

［片段4］運用模型，體會一致

師（出示圖10）：只能用邊長為1厘米的正方形測量長方形或正方形的面積嗎？能不能用給定的正方形量一量長方形的面積？

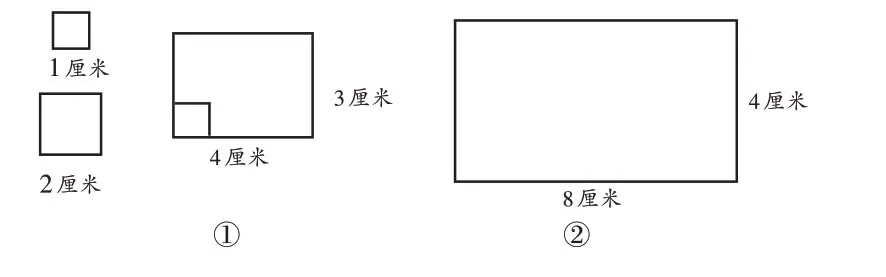
圖10

生1：邊長為1 厘米的正方形面積是1 平方厘米，所以圖形①的面積是4×3=12（平方厘米），圖形②的面積是8×4=32（平方厘米）；邊長為2厘米的正方形面積是4 平方厘米，測量圖形②的面積時一共擺8 個，所以圖形②面積是4×8=32（平方厘米），但是測量圖形①時，不能正好擺滿。

師（出示圖11）：測量圖形的面積和測量線段的長度之間有什么相同的地方嗎？

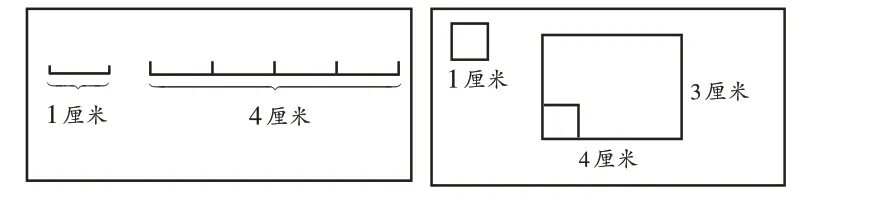
圖11

生2：測量線段是看有幾個長度單位；測量面積是看有幾個面積單位。

師（出示圖12）：在以后的學習中，測量物體的體積還會用到這樣的方法。

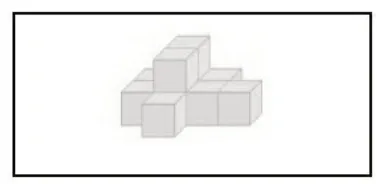
圖12

［設計意圖］學生通過比較，發現用邊長為2 厘米的正方形測量圖形②更方便，但是測量圖形①卻有困難。用邊長為1 厘米的正方形既能測量圖形①也能測量圖形②，在對比中從度量角度理解了像1 厘米、1 分米，以及1 平方厘米、1 平方分米這些數學中規定的常用長度和面積單位有其合理性，是選擇的結果。

三、教后反思

一般來說，兒童建構“面積測量”這個“概念”需要經歷三個階段：首先，6 歲左右的兒童可以在具體操作活動中建構面積守恒的觀念；其次，10 歲左右的兒童可以通過操作活動“發明”測量各種規則平面圖形面積的方法；最后，12 歲左右的兒童可以用純粹形式化的代數推理得出各種平面圖形的面積公式。

為了更精確地了解三年級學生的學習起點，通過前測了解學生對“面積”相關知識的掌握現狀，如混淆周長和面積的概念、會計算方法卻道不明理由等。在此基礎上，教師從學生的“已知”“已會”出發，重整教學資源，使學生在回顧測量長度的經驗的過程中初步感悟“單位測量屬性”；在操作活動中體悟數值相等背后是“單位面積個數”與“長方形面積”的對應關系；在推理思辨中領悟如何用“一維線段”刻畫“二維面積”；在拓展運用中以整體視角深刻理解線、面、體的“錨點”——單位的可累積性。“學”是“需求側”，表明在哪里；“教”是“供給側”，指向去哪里。只要立足學情調研、資源調配，抓住大概念的“錨點”，就能讓教學預期“可及”，也能實現“學”與“教”的“共振”。