基于機器學習的低彈性模量鈦合金建模和預測的研究

潘 登， 李 謙， 李 強

（1. 上海大學 材料基因組工程研究院, 上海 200444；2. 上海理工大學 機械工程學院, 上海 200093）

目前，鈦合金已經在人工關節、牙科種植和外科器械中得到了廣泛使用，但是鈦合金的生產工藝相對復雜，加工難度大，造成成本較高，限制了其廣進一步發展[1]。目前，大范圍使用的鈦合金成分為Ti-6Al-4V 合金（TC4 鈦合金），醫學臨床研究發現，TC4 鈦合金在人體內會向血液釋放Al 離子和V 離子，這些離子會誘發阿爾茲海默癥、神經系統病變、骨骼軟化癥等疾病。TC4 鈦合金的彈性模量遠高于人骨的，因此，會造成“應力屏蔽”現象，不利于新骨的生長。近年來，通過加入不同配比的合金元素（如Ta、Mo、Nb），獲得匹配人骨彈性模量的高強度無毒β 型鈦合金是目前醫用材料研究的重要方向之一[2]。

計算相圖是一種常用的設計方法，它基于熱力學平衡原理和試驗數據，并結合了計算機模擬和優化算法，旨在提供對合金體系中各種相的形成和穩定性的深入理解。盡管計算相圖方法在預測和計算相圖方面非常有用，但它仍然依賴于試驗數據和熱力學數據庫的準確性。鈦合金的制備和加工較為復雜，組成元素種類繁多，大幅增加了材料性能試驗量，所以會造成上述性能測試方法成本高、周期長、效率低，給新型鈦合金的開發帶來了諸多挑戰。

基于數據驅動方式的機器學習建模無需明確內部的復雜機制，僅依靠數據訓練來構建關系模型，目前已成為材料研究的熱點之一[3-5]。主要的機械學習方法有多層感知器（multi-layer perceptron,MLP）、卷積神經網絡（convolutional neural networks,CNN）、隨機森林網絡（random forest regression,RFR）等。MLP 是一種常見的前饋神經網絡模型，由多個節點組成的多個隱藏層構成，每個節點都是一個人工神經元，接收來自前一層的輸入，并將加權和輸入進行非線性變換后傳遞給下一層[6]。CNN 是一種依靠卷積核從輸入數據中提取局部特征，并通過卷積核的滑動獲得輸入數據特征圖的神經網絡[7]。RFR 是一種集成學習方法，通過組合多個決策樹模型來進行預測和分類[8-9]。采用機器學習的方法，是從數據和算法的角度建立模型，揭示數據和性能的相關性和顯著性，在合金成分設計和性能預測方面具有一定的指導意義[10-13]。

上世紀80 年代末，日本學者Morinaga 等[14]提出，采用反映元素電負性的d-電子結合能（Md）和反映d 軌道電子結合強度的d-電子結合次數（Bo）來評估元素原子尺寸、電負性及合金化等因素的影響。各合金元素的Md和Bo按照原子分數取加權平均值，即為合金的d-電子平均結合能（）和d-電子平均結合次數（）的影響水平。根據計算結果可以確定合金的相穩定性，為合金設計提供理論依據。Mo 當量（[Mo]）常被用于鈦合金中確定β 相的穩定程度。本文針對鈦合金彈性模量快速預測的需要，利用已有的鈦合金彈性模量，并通過合金設計公式轉換得到鈦合金的[Mo]、、三種參數作為原始數據；基于數據驅動建立鈦合金元素配比與其彈性模量關系模型，并對模型預測性能進行驗證與對比分析。

1 機器學習過程

1.1 合金元素數據轉換與分析

基于鈦合金設計公式及機器學習的多層感知器理念建立數學模型，利用模型揭示鈦合金元素配比與彈性模量之間的關系。圖1 是模型數據集轉換流程。

首先，數據集收集具有β 相的鈦合金數據，使用箱型圖描述這個數據集的樣本分布，橫軸為不同參數的名稱，縱軸為相應元素參數值；然后，利用相應公式轉換成為、、[Mo]三種參數作為相關模型原始輸入數據直接進行處理，轉換公式為：

式中：xi為 合金元素i的 原子分數； （Bo）i為合金元素i的Bo值； （Md）i為合金元素i的Md值[15]。在數據集進行轉換之后依舊使用箱型圖描述這個數據集的樣本分布，用來分析數據集的稀疏值和異常值。

數據集經過轉換后，只有[Mo]、3 個輸入標簽值，利用斯皮爾曼（Spearman）計算方法來獲得三者與彈性模量之間的相關性熱力圖與相應的P值判斷相關性的顯著程度。

通過Spearman 計算所得的P值是用于衡量兩變量相關性是否具有統計學上顯著性的指標。Spearman 相關性系數衡量了兩個變量之間的線性強度，取值范圍為-1～1。

相關性ρ計算公式如下：

式中：R（x）為x元素的當前取值；R（y）為y元素的當前取值；為x元素的平均值；為y元素的平均值；n為元素觀測總數。

在訓練過程中，所有模型將數據集按照8:2 的比例進行分割，其中80%用于模型訓練，20%作為測試集驗證模型性能。為提升模型在訓練過程中的收斂速度，將數據集送入模型前進行歸一化處理，并采用式（5）將輸入量歸一化至區間[0, ε]，采用式（6）將輸出量歸一化至區間[-ε, ε]。

式中：x、y分別為轉化后的輸入標簽值以及合金的彈性模量；x′、y′分別為歸一化后所得相應輸入、輸出值； ε為縮放系數。

鈦合金中，鈦占比一般不超過80%，因此，本文將 ε設定為0.8。

1.2 機器學習模型的建立

本文分別使用CNN、RFR 和MLP 三種模型，通過Python 軟件進行建模和計算。

1.2.1 MLP 模型

圖2（a）為MLP 模型的訓練示意圖，其中，輸入層接收原始數據或特征向量作為輸入，隱藏層進行加權和非線性變換，輸出層根據具體任務產生相應的輸出結果。隱藏層和輸出層之間的連接由權重參數決定，各層之間皆使用激活函數進行連接，這些參數通過訓練進行優化。

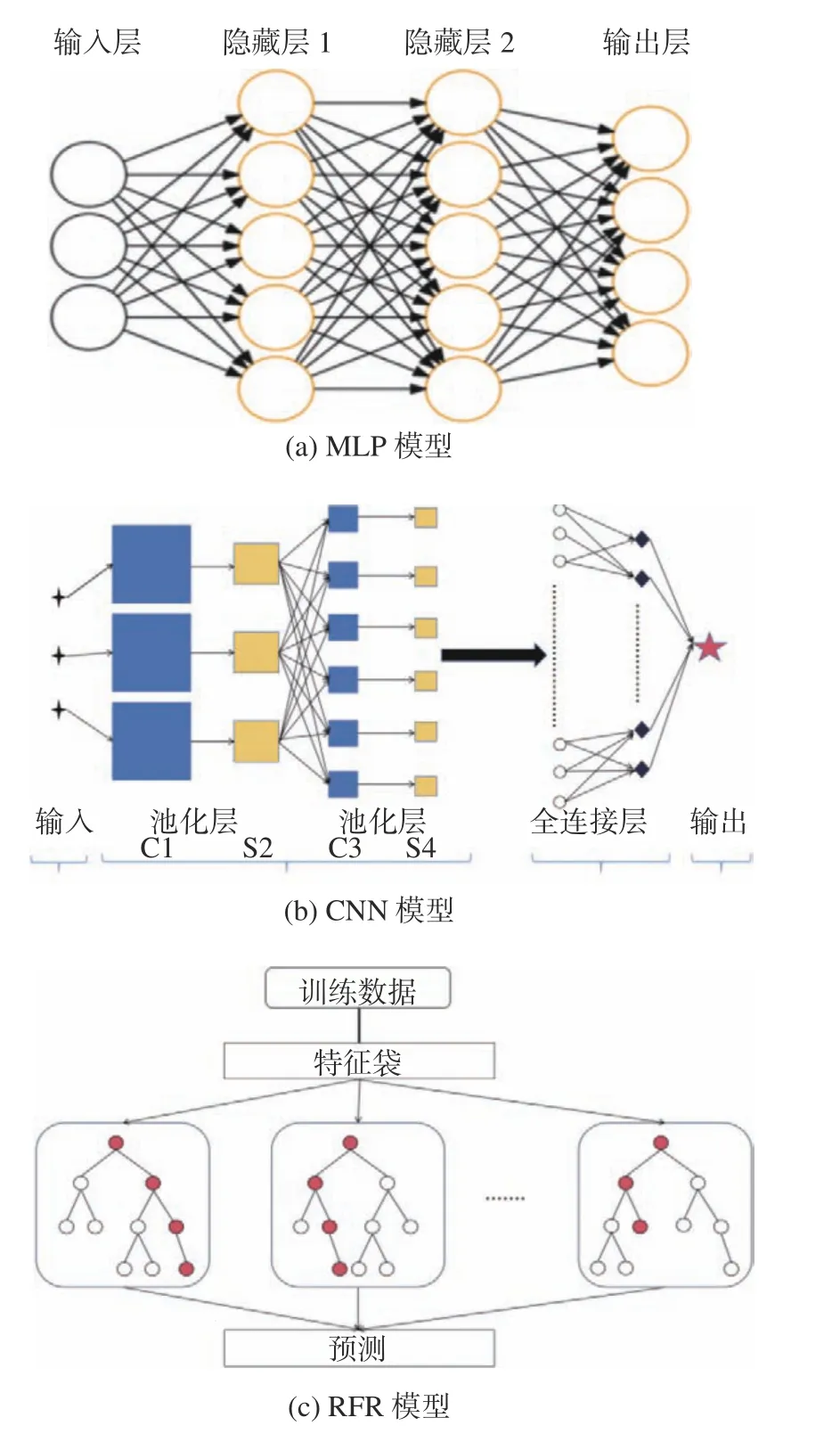
圖2 三種模型內部結構圖Fig. 2 Internal structure diagrams of the three models

MLP 模型的核心思想是通過非線性變換（通常是使用激活函數）將輸入數據映射到更高維的特征空間。MLP 模型的訓練方法通常使用反向傳播算法，該算法通過計算損失函數對于權重參數的梯度，不斷調整權重參數以最小化損失函數。具體表達如下：

式中：y為輸出值；hk為輸出層神經元的輸入加權和。R為使用的激活函數為整流線性函數（rectified linear unit,R），其表達式為：

在神經網絡中，R函數的導數恒為1 或0，不存在梯度消失的問題，因此，能夠更好地訓練深層神經網絡。R函數在輸入值為負時輸出為0，因此，可以使神經網絡中的一部分神經元處于關閉狀態，增加了網絡的稀疏性，減少了模型的復雜程度[16]。

1.2.2 CNN 模型

CNN 模型（見圖2b）在經過多個卷積、池化操作后，能挖掘數據中隱含的深層特征[17-18]，CNN模型中卷積層公式如下：

式中：W為圖像寬度；H為圖像高度；S為卷積核步長；p為圖像邊緣增加的邊界像素層數。

在CNN 模型中，輸入數據只能是圖片，所以對于轉換后的合金元素數據進行圖像化三維處理，隨后放入CNN 模型中進行訓練。

1.2.3 RFR 模型

RFR 模型（見圖2c）通過構建多個決策樹，并對它們的結果進行綜合，從而提高了整體預測的準確性和穩定性。每個決策樹都是獨立的分類器，最后預測結果由所有決策樹的投票或平均所決定。RFR 模型的優點包括具有處理高維數據和大規模數據集的能力、對缺失值或異常值的魯棒性較強、參數調整需求較少[19-24]。

1.3 機器學習模型的預測

為量化各個預測模型在驗證集上的預測性能，評價指標采用相關指數（r-square,R2），均方根誤差（root mean square error, RMSE）兩種性能指標對模型性能進行量化，RMSE 指標越小表明模型預測性能越優，R2 指標越趨近于1，則模型預測能力越具有可信度，R2 指標公式如下[25-28]：

式中：yi為 觀測值；為回歸模型預測值；為所有實際觀測值的均值。

RMSE 公式如下：

式中：ti為 每一批次計算過程中的標簽；yi為每一批次計算過程中的輸出。

所有模型訓練完成后，儲存相關系數和權重，將數據集中20%未經訓練的數據作為驗證數據放入模型中進行驗證，通過比較其RMSE 和R2 指標來判斷各個模型的優劣[28]。

RFR 模型作為機器學習模型在參數確定的情況下，預測性能指標均為確定值[29-31]，而CNN 模型和MLP 模型具有特殊的結構，對具有神經網絡結構的模型進行多次預測，對預測結果取平均值，比較性能優劣來判斷模型預測性能。本文將分別對CNN 模型、MLP 模型進行5 次訓練和預測[32-35]。

2 結果與討論

2.1 數據集分析

圖3 為未轉換前數據的箱型圖。在數據集中，鈦合金中的Ti 最大質量分數為88.2%，彈性模量分布在24.7～116.0 GPa。圖3 中除了Ti 以外，Nb 質量分數中位數高于其他合金元素，它是開發低彈性模量鈦合金時添加最多的合金元素。其次是Zr，它與Ti 同屬一族，具有與Ti 相似的物理化學性質，可用于強化合金和調整β 相穩定性。數據集中，三元和四元鈦合金最多，所以，鈦合金數據集中一組合金成分常常缺失一種或多種合金元素，從而導致數據集具有較強的稀疏性。由于這些合金元素在數據集中稀疏性太大，所以它們配比中位數接近零。需要指出的是，稀疏性太大的數據集對于神經網絡訓練是非常不利的。

圖3 數據集未轉換前合金元素統計箱型圖Fig.3 Statistical box plot image of the alloy elements before dataset conversion

圖4 是數據集轉換后參數統計箱型圖。圖4 中除了[Mo]參數以外，、兩個輸入值幾乎沒有異常數據，通過鈦合金成分設計公式轉換得到的數據集稀疏性減少，為模型的訓練提供更適合的原始數據，更有利于模型的訓練和擬合。

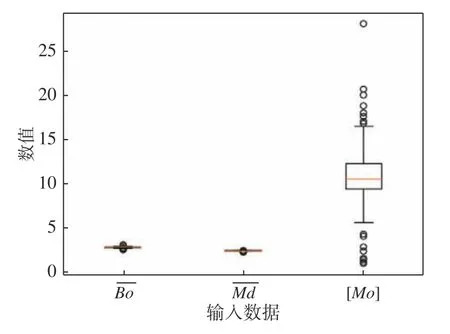
圖4 數據集轉換后參數統計箱型圖Fig. 4 Statistical box plot image of the parameter after dataset conversion

2.2 參數與彈性模量的相關性分析

圖5 是采用Spearman 系數計算數據集各參數同彈性模量所得的相關性系數的熱力圖。如果計算得到的Spearman 相關性系數具有較小的P值（通常小于選定的顯著性水平，如0.05），則可以認為觀察到的相關性系數不太可能是由隨機因素導致的，存在著真實的相關性。這意味著可以拒絕零假設，并認為兩個變量之間存在顯著的線性相關性。由圖5可知，[Mo]與鈦合金的彈性模量（E）相關性最大，相關性系數為0.29。在本文數據集中反映出[Mo]與彈性模量呈正相關；在數據集中與彈性模量的相關性系數為-0.22，說明與彈性模量之間呈負相關；與彈性模量相關性系數為-0.10，說明與彈性模量呈負相關。

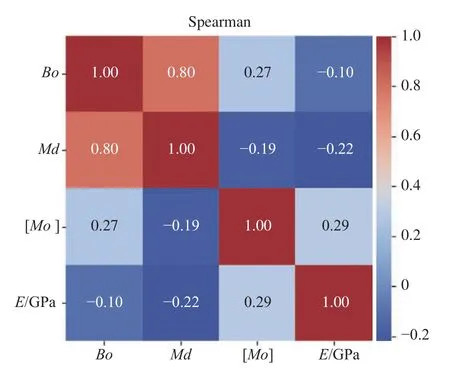
圖5 采用Spearman 系數計算數據集各參數同彈性模量（E）所得的相關性值的熱力圖Fig. 5 Heat chart of the Spearman coefficient-calculated correlation value between each parameter in the dataset and elastic modulus （E）

表1 是通過Spearman 計算所得數據集之間的P值，彈性模量與[Mo]、之間的相關性＜0.05，它們之間具有顯著的相關性。與彈性模量的P值＞0.05，所以和鈦合金的彈性模量不具有明顯的相關性。

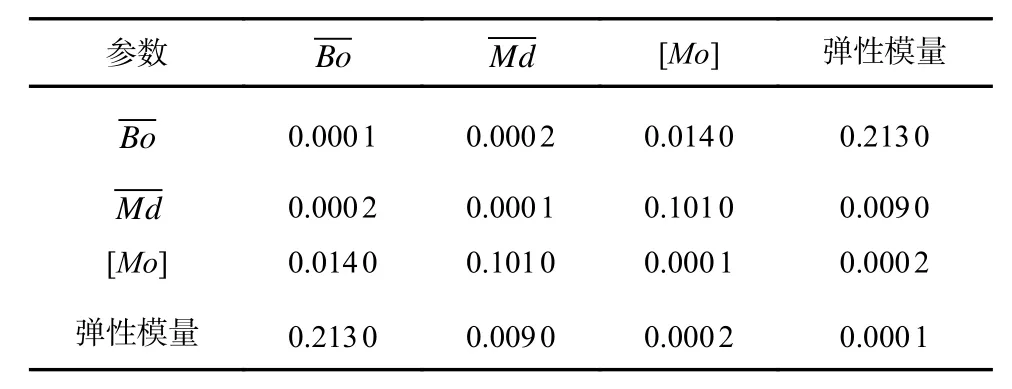
表1 數據集參數之間的P 值Tab.1 P-values between the parameters in the dataset

Bo、Md、[Mo]三者之間的P值＜0.05，所以它們之間具有顯著的相關性，這說明對于鈦合金的彈性模量的影響是間接的。

2.3 模型比較

三種模型經過計算和迭代后，最終確定MLP 結構為3-8-10-1，因此模型的輸入節點為3，隱藏層第一層節點數為8，隱藏層第二層節點數為10，最后輸出層的節點為1；CNN 模型采用10 個3×3 的卷積核，全連接層節點數為128；RFR 模型的決策樹數量為120。

圖6 是訓練好的MLP、CNN、RFR 模型對驗證集數據進行驗證所得預測對比圖。圖6 中紅色點線為驗證集中鈦合金所對應的實測彈性模量，而藍色則是模型通過大量訓練以后預測所得到的相應合金的彈性模量，可以看出，MLP 模型可以很好地去模擬合金的元素配比和彈性模量之間的相應關系，預測值的數據和實測值的數據較為貼合，具有可靠預測合金性能的能力。

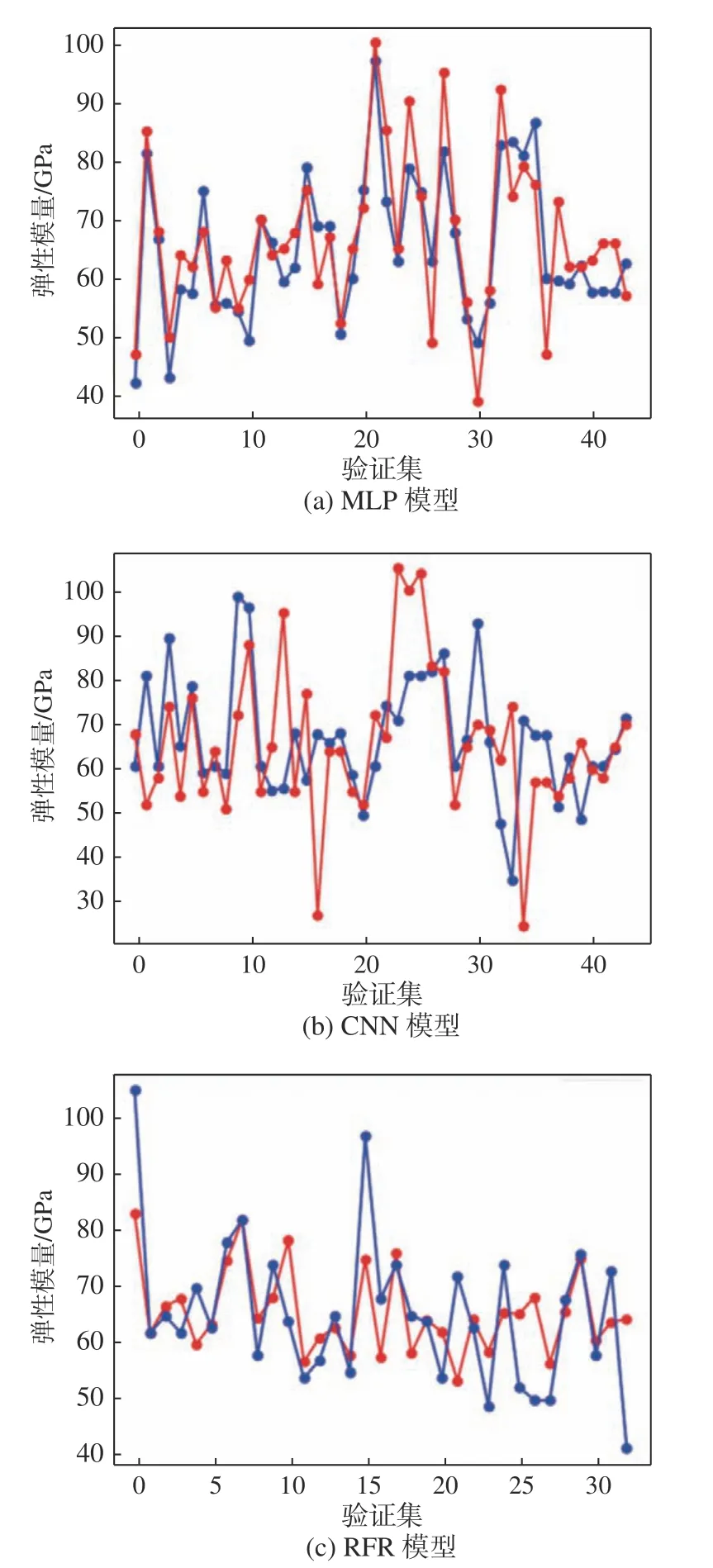
圖6 機器學習模型驗證集預測圖Fig. 6 Prediction images of the validation sets obtained by machine learning models

表2 為預測模型性能指標。從表2 可以看到，MLP 模型的RMSE 和R2 指標平均值分別是7.54 GPa和0.66；CNN 模型的RMSE 和R2 指標平均值分別是3.58 GPa 和-0.61；RFR 模型的RMSE 和R2 指標平均值分別是10.03 GPa 和0.40。當R2 的評分大于0 時才能證明模型的預測結果具有可信度，比較三者R2 評分可知，MLP 模型對于鈦合金彈性模量的預測建模是可信度最高的。RMSE 代表預測結果和實際模量之間的偏差，MLP 模型的RMSE 于3 個模型中處于中游。在模型評價中，R2 指標的權重大于RMSE 的，模型的第一評價標準是R2。綜合可知，MLP 模型在本文數據集中的預測性能最佳，CNN 模型具有一定的預測能力，但是可靠性不高，RFR 模型的預測能力介于二者之間。MLP 模型綜合性能指標相較于其他兩個模型更具優勢，模型預測結果更為可靠。

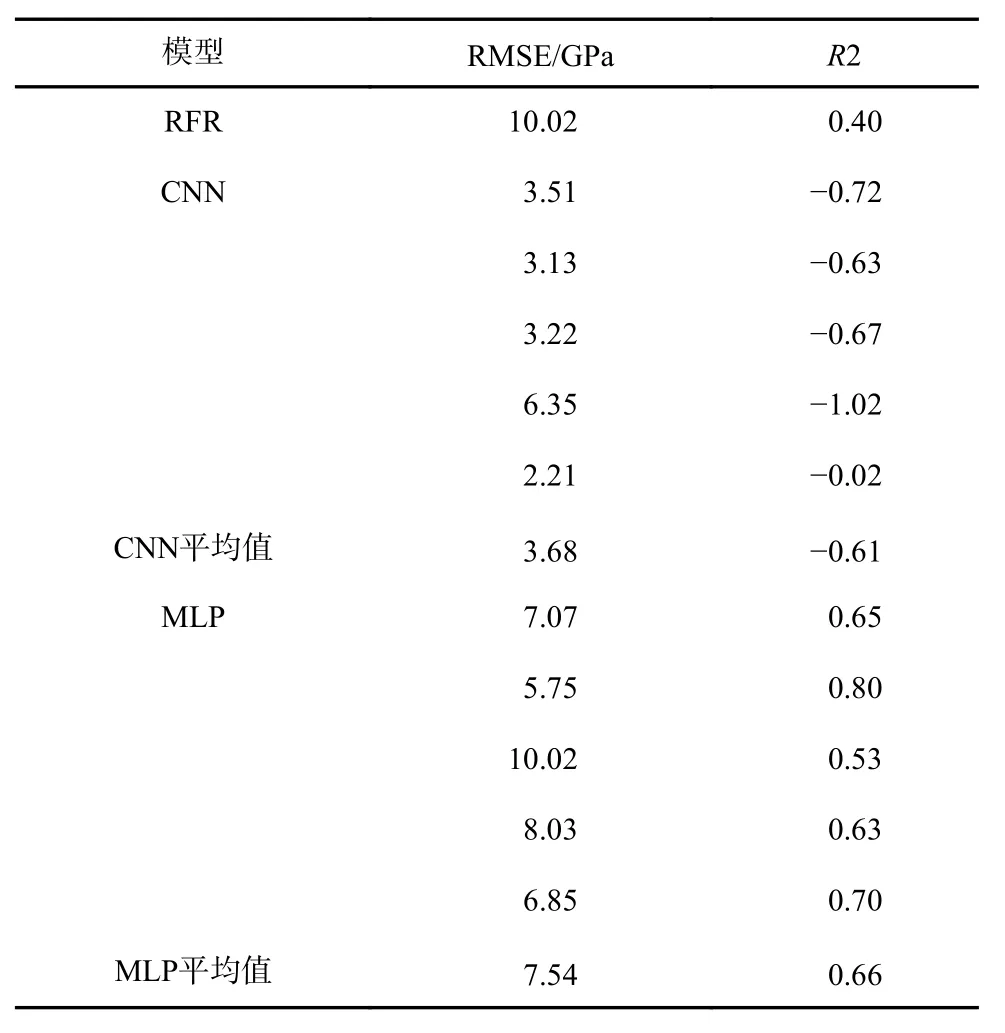
表2 預測模型性能指標Tab.2 Performance indicators of the prediction models

為了更加直觀地表達MLP 模型在全部數據集上的預測效果，通常采用擬合優度圖進行直觀判斷。圖7 是MLP 模型對所有數據集的預測擬合圖，圖中藍色圓形點集表示模型在訓練集的預測值，紅色圓形點集表示模型在測試集上的預測值。從圖7 中可以看出，MLP 模型在測試集上的預測值大部分靠近中心線，數據散點分布更緊湊，表明預測值更接近實際值。圖7 也反映了MLP 模型對數據集的較好擬合情況。

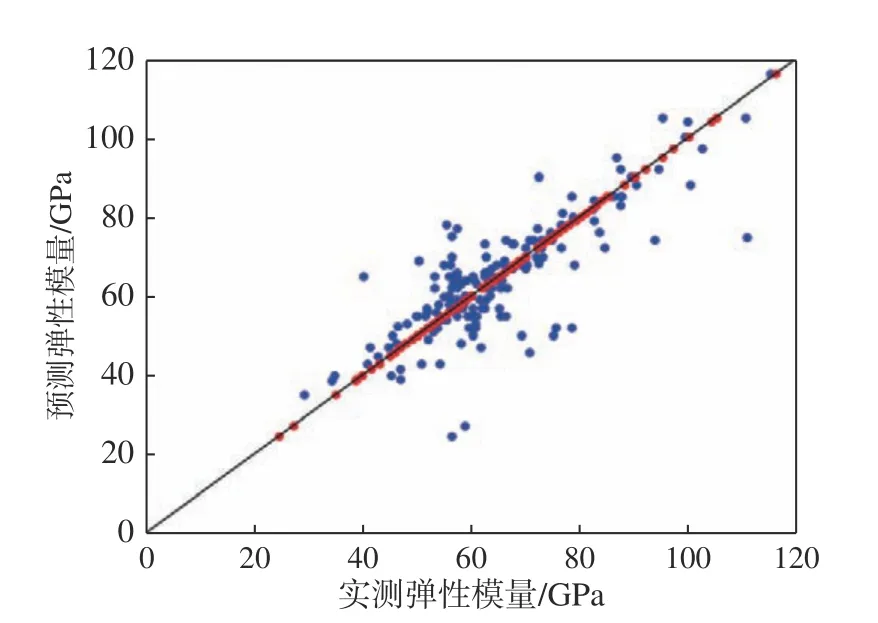
圖7 MLP 模型擬合圖Fig.7 Fitting graph of the MLP model

2.4 預測結果

為了進一步說明MLP 模型的可靠性，從測試集中選取5 組常見的鈦合金進行模型預測分析。表3是5 組常見鈦合金的彈性模量實測值與預測值，二者的偏差在MLP 模型的RMSE 范圍內，說明預測結果均是合理的，即MLP 模型的預測能力是可靠的。

表3 5 組常見鈦合金的彈性模量實測值與預測值Tab.3 Measured and predicted elastic moduli of five groups of common titanium alloys

3 結 論

本文利用合金設計公式轉換后的數據集作為原始數據集，建立機器學習模型。通過驗證和分析模型的預測性能，得出以下結論：

（1）利用合金設計公式對原始數據集進行轉換，解決了原始數據集稀疏值較大的問題。

（2）彈性模量的大小與[Mo]呈顯著的正相關，與呈顯著的負相關，而與彈性模量之間無顯著相關性。通過影響[Mo]、來間接影響鈦合金的彈性模量。

（3）建立了基于CNN、REF、MLP 的三種鈦合金彈性模量預測模型。其中，MLP 模型對鈦合金彈性模量預測的RMSE、R2 指標平均值分別為7.54 GPa、0.66，相較于RFR 模型、CNN 模型，MLP 模型具有更優的預測性能和預測精度。