實驗與探究:三角形中邊與角的不等關系
李燕
一、素養目標
通過觀察、實驗探究、動手操作、以及推理論證等數學活動,對三角形邊與角之間的不等關系進行探索分析,發展學生的發現問題、分析問題和解決問題的能力,讓學生學會用數學的眼光看問題,數學的思維思考問題,數學的語言描述并解決問題;通過課前自我準備、課上小組交流、個人展示等數學活動,讓學生知道數學學習是充滿著探索與創新的,激發學生學習幾何的興趣,獲得解決問題的成功體驗; 通過視覺直觀感受和數據收集整理比較大小讓學生發現規律,得出猜想,再通過動手折紙中的折痕添加輔助線,抽象出截長補短等方法來構造全等三角形的經驗,利用三角形邊角相等的轉化解決邊角之間的不等問題,發展嚴謹的數學理性思維。
二、實驗資源
希沃白板5、有刻度直尺與量角器、圓規、統一的不等邊三角形ABC剪紙(AB>AC)、幾何畫板。
三、實驗設計與創新點
實驗設計:通過四種方法逐步得到猜想與證明。
(一)目測(產生想法);(二)通過每位同學任意畫不等邊三角形測量邊角得到隨機數據,隨機抽取兩組數據比較不等邊與其對角的大小,直觀感受三角形邊角之間的不等關系得出猜想;(三)準備不等邊三角形ABC(AB>AC)剪紙四張,通過折紙方法驗證猜想,并利用幾何畫板演示翻折過程,學生更直觀形象感受方法與思想,幫助學生抽象出數學方法(通過折痕添加輔助線);(四)學生獨立添加輔助線轉化角,利用三角形邊角相等的轉化解決邊角之間的不等問題,發展嚴謹的數學推理思維,方法多樣,萬法歸一,得出結論與幾何模型。
創新點:通過目測——測量——折紙——證明四個角度與層次得出并證明猜想 ,多角度思考問題,從具體到抽象,歸納出結論和截長補短等模型。
四、教學過程
(一)回顧舊知,引入課題
1.回顧舊知:教師通過折紙剪出等腰三角形,帶領學生回顧等邊對等角(等角對等邊)的性質與判定。
2.引入課題:在剪出三角形ABC中,AB=AC,∠B=∠C。
問:在剪紙三角形ABC中,目測一下AB與BC相等嗎?
答:不相等。一個不等邊三角形中,會存在不相等的邊,那不相等的邊所對的角之間的大小關系呢?就是本節課研究的內容.
設計意圖:回顧舊知,通過折疊直觀復習等腰三角形的性質與判定,為探究做好知識與經驗鋪墊;通過剪出圖形教師追問引出本節課的重點問題,吸引學生注意,調動學生的好奇心。
(二)探究新知
問1:在剛剪的等腰三角形ABC中,AB與BC目測一下哪條邊更長?AB所對的角是哪個?BC所對的角是哪個?它們相等嗎?哪個角更大?
答:AB;∠C;∠A;不相等;∠C。
問2:從目測來看三角形中,不相等的邊越長所對的角越怎么樣?
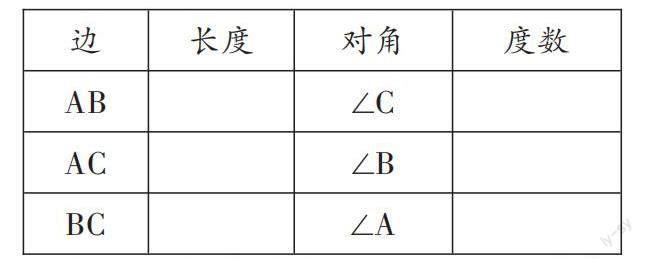
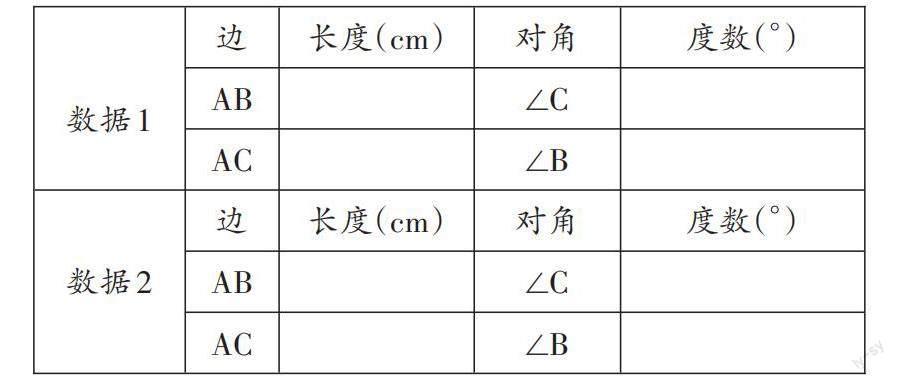
答:越大。學生準備:請同學們任意畫一個不等邊三角形ABC,測量所畫三角形三條邊的長度和各邊所對角的度數,并記錄在表格中。
學生活動1:比較這兩條邊的大小,再比較它們所對角的大小,請猜想三角形中不相等的邊所對角之間的大小關系是怎樣的?
猜想:在一個三角形中,如果兩條邊不等,那么他們所對的角也不等,大邊所對的角較大.
簡寫:大邊對大角。
設計意圖:通過目測比較大小引出思考,培養學生用數學的眼光看世界,但是數學是嚴謹的學科,為了進一步求證想法,讓學生通過動手畫不等邊三角形,既排開特殊圖形,又具有隨機性,使得初步探究更具有說服力;通過測量,隨機抽取,比較數據大小,直觀感受,進一步得出猜想。
(三)折紙與證明
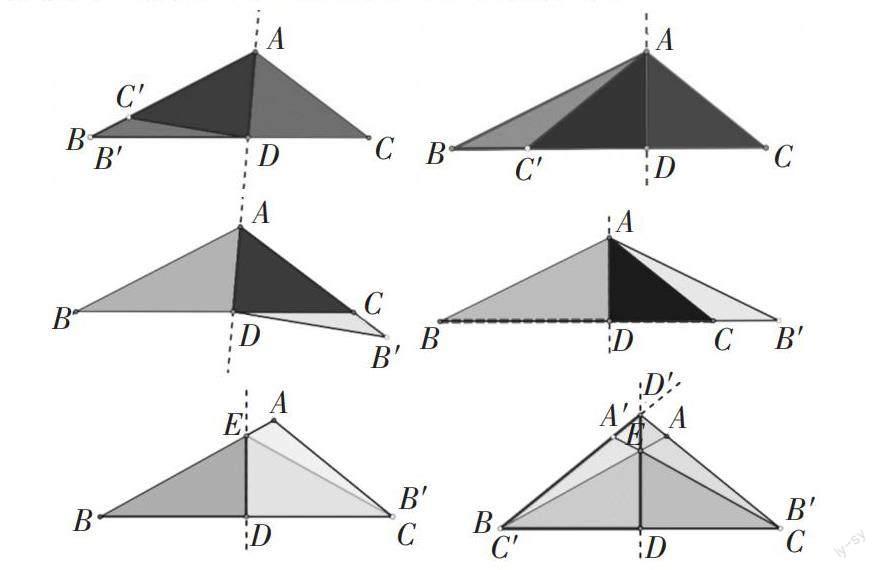
學生活動2:用準備好的四張三角形ABC(AB>AC)剪紙,通過折紙方法比較∠B與∠C大小,小組交流分享。
1.小組分享,教師觀察;2.學生上臺展示講解方法,教師在多個折法中挑一種重點分析講解,融入數學思想與證明思路提醒;3.教師通過幾何畫板直觀形象展示、補充不足、進行匯總對比引導。
活動3:根據活動2折痕添加輔助線,類比“等邊對等角”的探索流程,梳理小組匯總方法,證明活動1的猜想(如下)。
已知:在△ABC中,AB>AC,邊AB的對角為∠C,邊AC的對角為∠B.
求證:∠C>∠B.
方法1:
證明:作∠BAC的角平分線AD,交BC于點D,在AB上取一點E,使得AE=AC,連接DE。
∵AD為∠BAC的角平分線
∴∠BAD=∠CAD
在△AED和△ACD中
∴△AED≌△ACD(SAS)
∴∠AED=∠C
又∵∠AED=∠B+∠BDE
∴∠AED>∠B
∴∠C>∠B
方法2:
證明:在AB上取一點E,使得AE=AC,連接CE.
∵AE=CE
∴∠AEC=∠ACE
又∵∠AEC=∠B+∠BCE
∠ACB>∠ACE
∴∠AEC>∠B
∴∠ACB>∠B
方法3:作∠BAC的角平分線AD,交BC于點D,在延長AC至點E,使得AE=AB,連接DE.
∵AD為∠BAC的角平分線
∴∠BAD=∠CAD
在△AED和△ABD中
[AE=AB∠AED=∠BAD=AD(共邊)]
∴△AED≌△ABD(SAS)
∴∠E=∠B
又∵∠ACD=∠E+∠CED
∴∠ACD>∠E
∴∠ACD>∠B
結論:在一個三角形中,如果兩條邊不等,那么他們所對的角也不等,大邊所對的角較大(簡寫:大邊對大角)。
(四)課堂小結
1.三角形邊與角的不等關系:大邊對大角;2.探究新知思路:觀察—猜想—證明—結論;3.探究證明思路過程中用了轉化思想(未知轉化為已知),截長補短常思想;4.證明方法很多,但有很多共性—數學模型。
(五)課堂檢測
1.在△ABC中,已知BC>AB>AC,那么∠A,∠B,∠C有怎樣的大小關系?
答:∠A>∠C>∠B
2.如果一個三角形中最大的邊所對的角是銳角,這個三角形一定是銳角三角形嗎?為什么?
答:是;因為三角形中最大的邊所對的角是銳角,由“大邊對大角”可知這個三角形最大的角為銳角,所以這個三角形一定是銳角三角形。
(六)教學反思
在實驗過程中,教師由折紙剪出等腰三角形,巧妙復習了等腰三角形邊角關系以及證明邊角關系的啟迪思想——軸對稱性質;通過追問引導學生看出不等邊與對角的大小關系,引出思考。又從學生任意畫不等邊三角形入手,避開特殊性,通過測量法與比較大小得出不等邊三角形邊角不等關系猜想(特殊到一般需要嚴謹證明),再給出一個滿足猜想的三角形ABC(AB>AC),要求學生通過折紙比較兩角大小,明確目標與方式。在具體實施過程中,教師不急于直接告訴學生輔助線的做法,而是通過課前設置“學習提示”給學生明確的實驗操作要求,引導學生在直觀地操作體驗中找到解決問題的方法,充分暴露學生探尋知識的思維過程,積累數學活動經驗,課上小組交流匯總,上臺展示,思維碰撞。學生由折疊的多樣性引發“一題多解”,多角度分析和解決問題,將具體性圖形抽象化,而萬法歸一提升學生對數學原理、通性通法的認識,提高思維的品質,感受數學方法之美和幾何圖形的對稱美。
美中不足的地方:1.由于大部分學生基礎偏弱,折紙討論過程中總結出來的方法比較少,學生沿高所在直線翻折的情況沒有找到,教師在用幾何畫板幫助學生更直觀感受折紙這個過程中忽略了學生不會折這個的問題,雖然給學會看了這個動態圖,但如果在帶著學生一起動手折一折可能效果更好。2.幾何畫板展示完后,教師忘記匯總,只是簡單講解后就提醒學生將“由折疊知”可以轉化為添加輔助線證明。學生添加輔助線的方法猜想證明更嚴謹,這是挺好的,學生總體都是截長的輔助線做法和疊合法,教師只做了口頭匯總對比,“補短”有所提醒,但由于課上時間有限就給學生留在了課下進行。如果可以再次將動態匯總圖放一起做總結,截長補短模型就更深入了。
(七)實驗作業
在一個三角形中,如果兩個角不等, 那么他們所對的邊也不等,大角所對的邊較大. 這個命題是真命題嗎?
要求:1.寫出命題的已知、求證并配圖;2.類比大邊對大角的研究流程,在作業本上完成此命題的證明。

